6.2 El problema de la colinealidad

Si alguna de las variables explicativas no aporta información relevante sobre la respuesta puede aparecer el problema de la colinealidad. En regresión múltiple se supone que ninguna de las variables explicativas es combinación lineal de las demás. Si una de las variables explicativas (variables independientes) es combinación lineal de las otras, no se pueden determinar los parámetros de forma única (sistema singular). Sin llegar a esta situación extrema, cuando algunas variables explicativas estén altamente correlacionadas entre sí, tendremos una situación de alta colinealidad. En este caso las estimaciones de los parámetros pueden verse seriamente afectadas:

  • Tendrán varianzas muy altas (serán poco eficientes).

  • Habrá mucha dependencia entre ellas (al modificar ligeramente el modelo, añadiendo o eliminando una variable o una observación, se producirán grandes cambios en las estimaciones de los efectos).

Consideraremos un ejemplo de regresión lineal bidimensional con datos simulados en el que las dos variables explicativas están altamente correlacionadas (en este caso además solo una de las variables explicativas tiene un efecto lineal sobre la respuesta):

set.seed(1)
n <- 50
rand.gen <- runif # rnorm
x1 <- rand.gen(n)
rho <- sqrt(0.99) # coeficiente de correlación
x2 <- rho*x1 + sqrt(1 - rho^2)*rand.gen(n)
fit.x2 <- lm(x2 ~ x1)
# plot(x1, x2)
# summary(fit.x2)

# Rejilla x-y para predicciones:
x1.range <- range(x1)
x1.grid <- seq(x1.range[1], x1.range[2], length.out = 30)
x2.range <- range(x2)
x2.grid <- seq(x2.range[1], x2.range[2], length.out = 30)
xy <- expand.grid(x1 = x1.grid, x2 = x2.grid)

# Modelo teórico:
model.teor <- function(x1, x2) x1
# model.teor <- function(x1, x2) x1 - 0.5*x2
y.grid <- matrix(mapply(model.teor, xy$x1, xy$x2), nrow = length(x1.grid))
y.mean <- mapply(model.teor, x1, x2)

Los valores de las variables explicativas y la tendencia teórica se muestran en la Figura 6.4:

library(plot3D)
ylim <- c(-2, 3) # range(y, y.pred)
scatter3D(z = y.mean, x = x1, y = x2, pch = 16, cex = 1, clim = ylim, zlim = ylim,
          theta = -40, phi = 20, ticktype = "detailed", 
          xlab = "x1", ylab = "x2", zlab = "y", 
          surf = list(x = x1.grid, y = x2.grid, z = y.grid, facets = NA))
scatter3D(z = rep(ylim[1], n), x = x1, y = x2, add = TRUE, colkey = FALSE, 
           pch = 16, cex = 1, col = "black")
x2.pred <- predict(fit.x2, newdata = data.frame(x1 = x1.range))
lines3D(z = rep(ylim[1], 2), x = x1.range, y = x2.pred, add = TRUE, 
        colkey = FALSE, col = "black")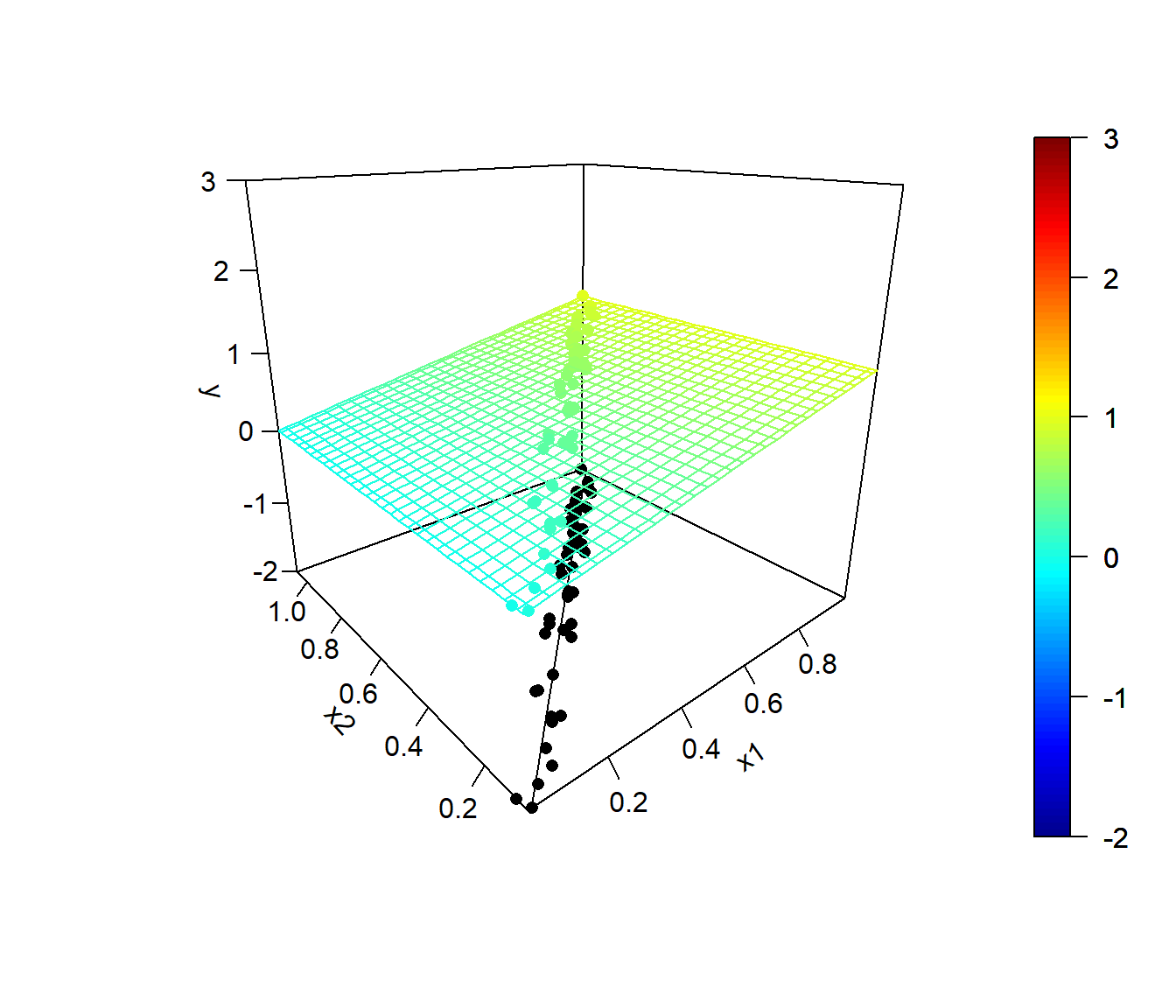
Modelo teórico y valores de las variables explicativas (altamente correlacionadas, con un coeficiente de determinación de 0.99).

Figura 6.4: Modelo teórico y valores de las variables explicativas (altamente correlacionadas, con un coeficiente de determinación de 0.99).

Para ilustrar el efecto de la correlación en los predictores, en la Figura 6.5 se muestran ejemplos de simulaciones bajo colinealidad y los correspondientes modelos ajustados. Podemos observar una alta variabilidad en los modelos ajustados (puede haber grandes diferencias en las estimaciones de los coeficientes de los predictores).

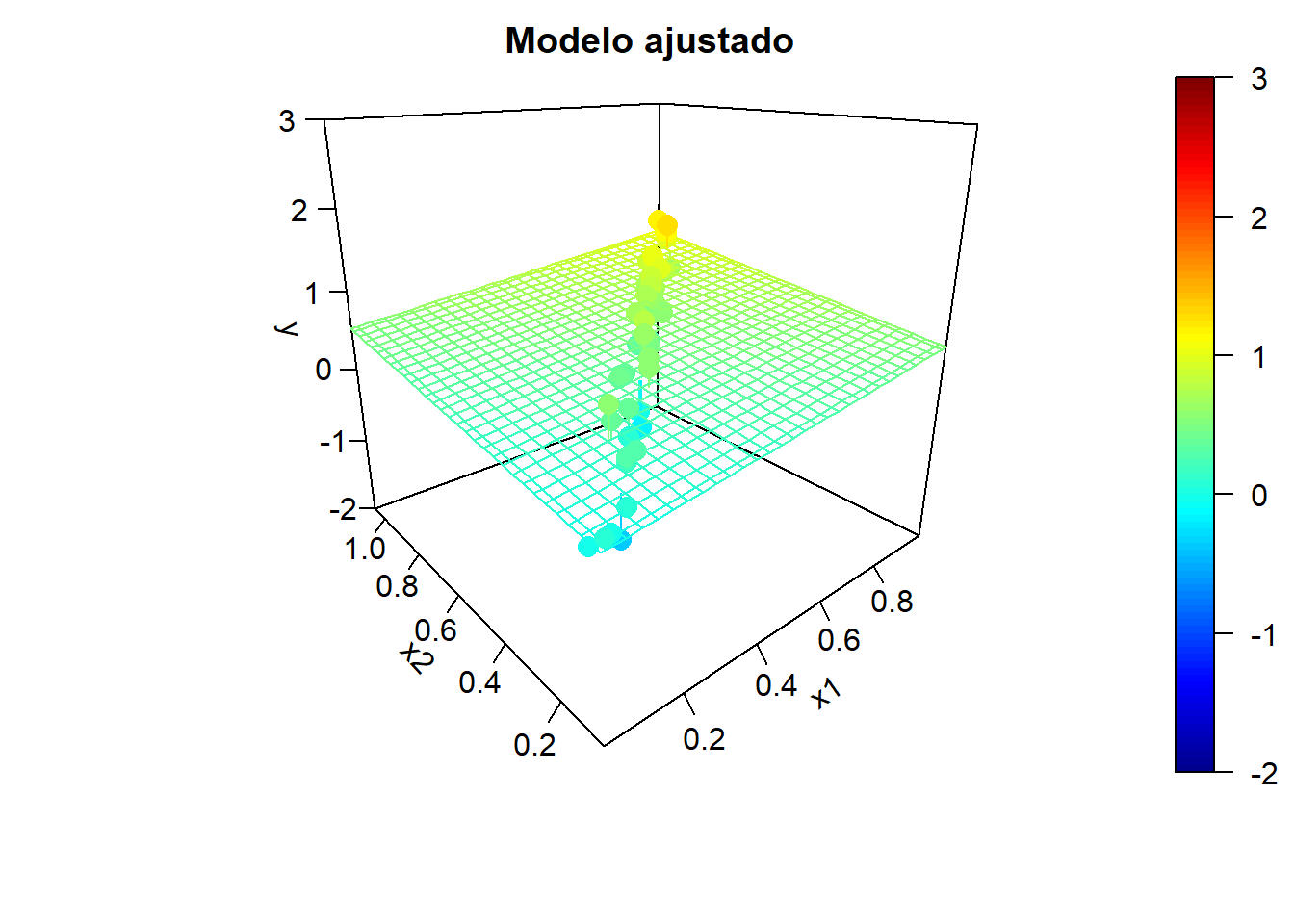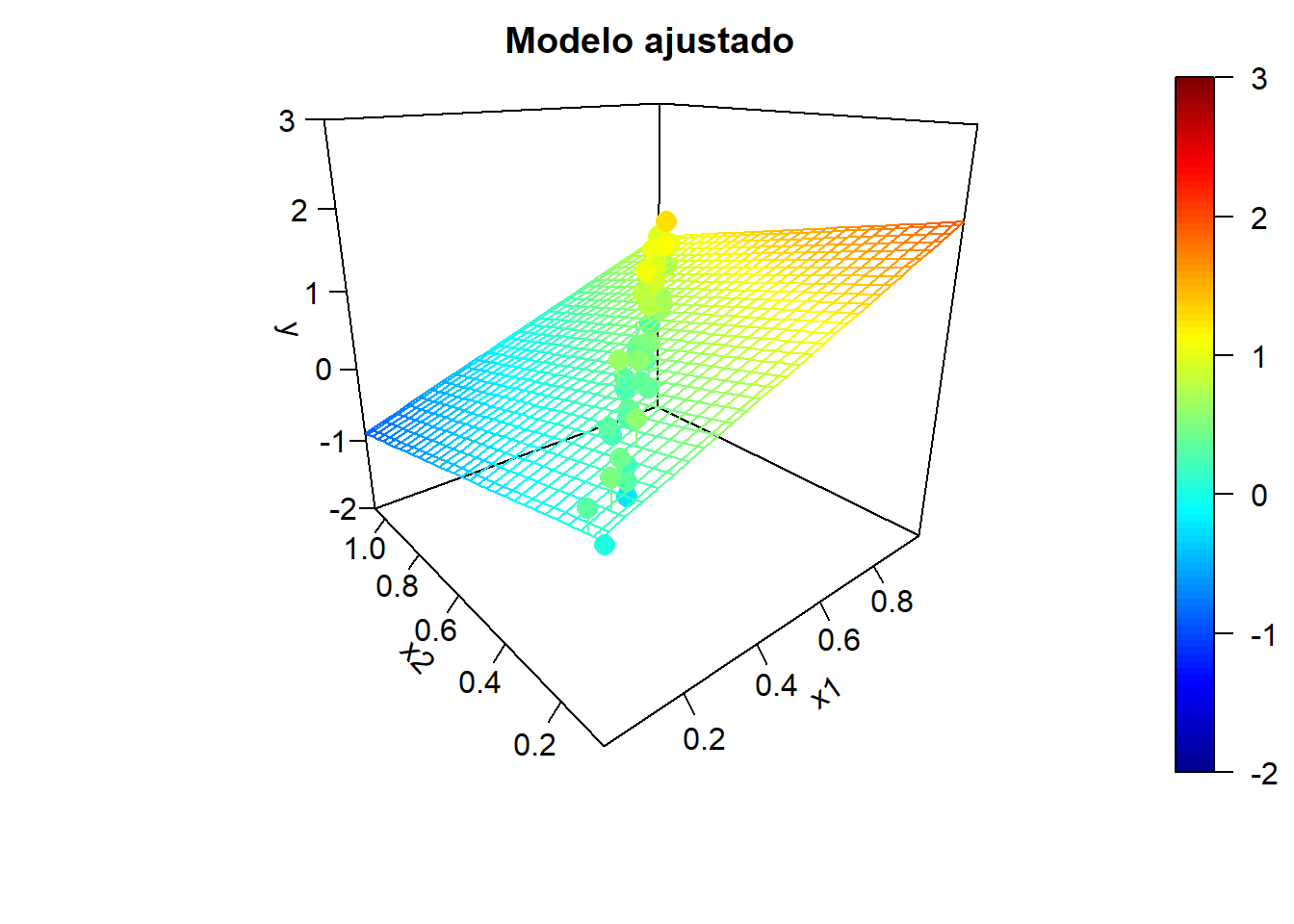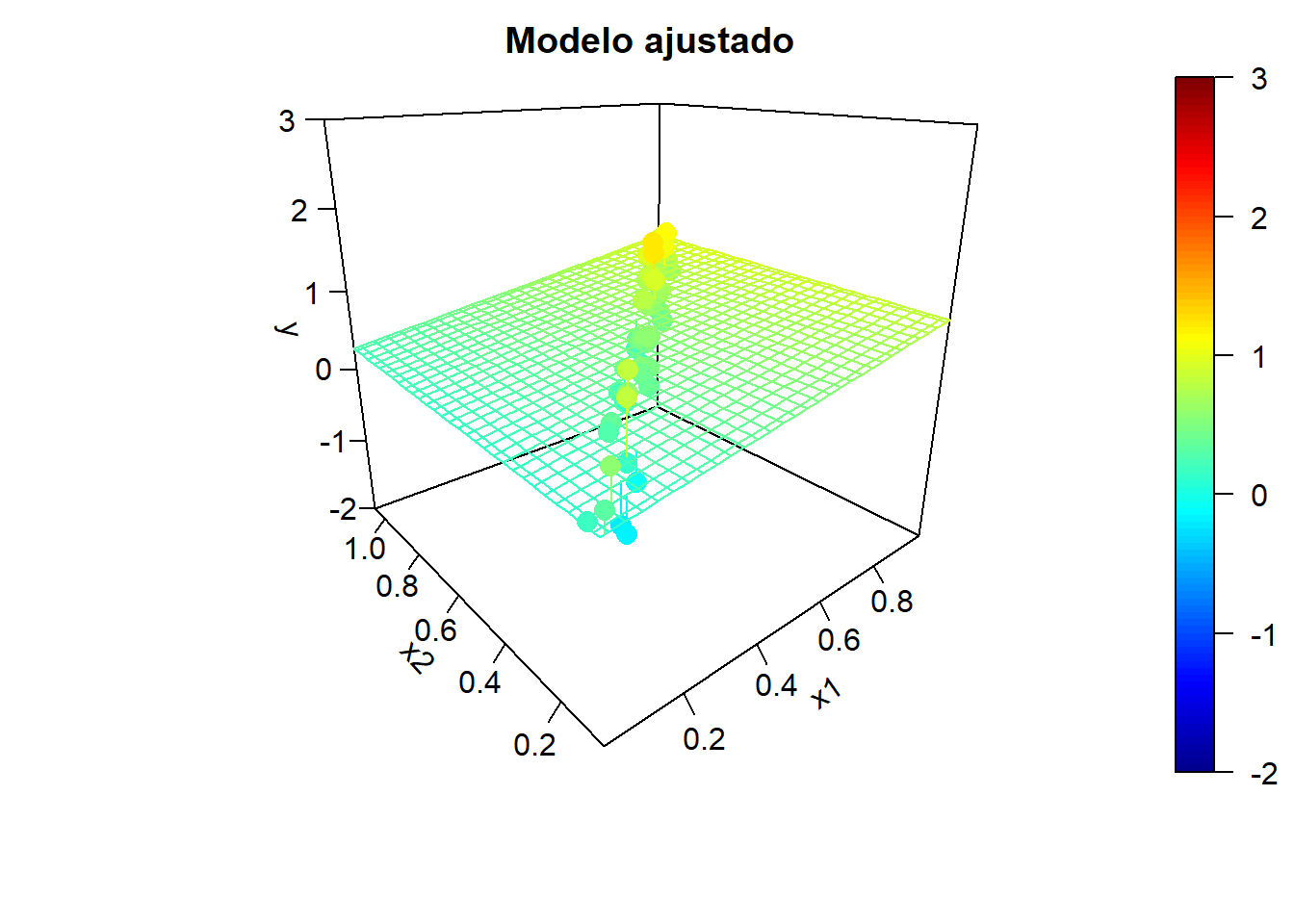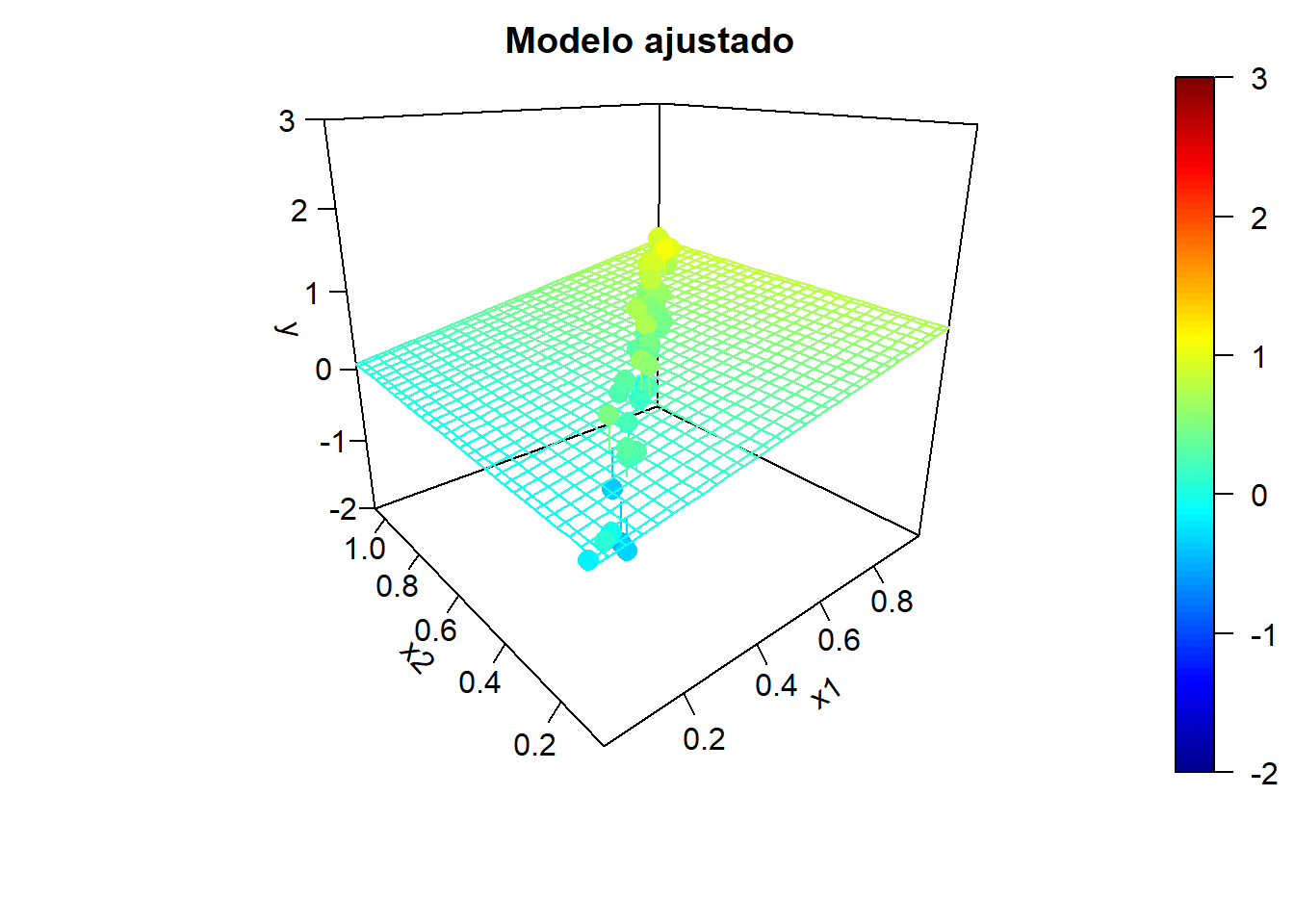
Ejemplo de simulaciones bajo colinelidad y correspondientes modelos ajustados.

Figura 6.5: Ejemplo de simulaciones bajo colinelidad y correspondientes modelos ajustados.

Incluso puede ocurrir que el contraste de regresión sea significativo (alto coeficiente de determinación), pero los contrastes individuales sean no significativos. Por ejemplo, en el último ajuste obtendríamos:

summary(fit)
## 
## Call:
## lm(formula = y ~ x1 + x2)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.45461 -0.13147  0.01428  0.16316  0.36616 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.11373    0.08944  -1.272    0.210
## x1           0.87084    1.19929   0.726    0.471
## x2           0.16752    1.19337   0.140    0.889
## 
## Residual standard error: 0.2209 on 47 degrees of freedom
## Multiple R-squared:  0.6308, Adjusted R-squared:  0.6151 
## F-statistic: 40.15 on 2 and 47 DF,  p-value: 6.776e-11

Podemos comparar los resultados anteriores con el caso de predictores incorrelados (Ver Figura 6.6):

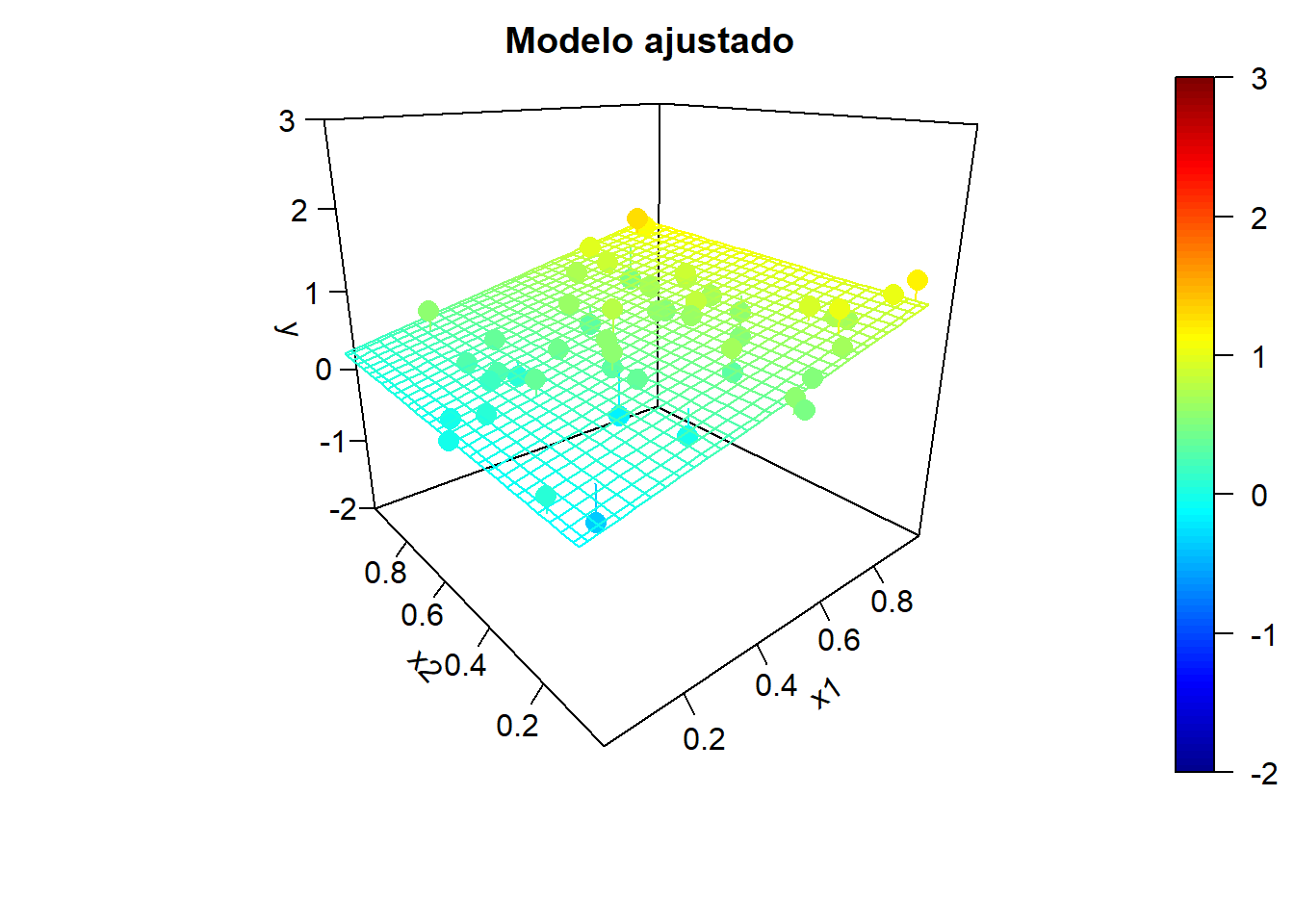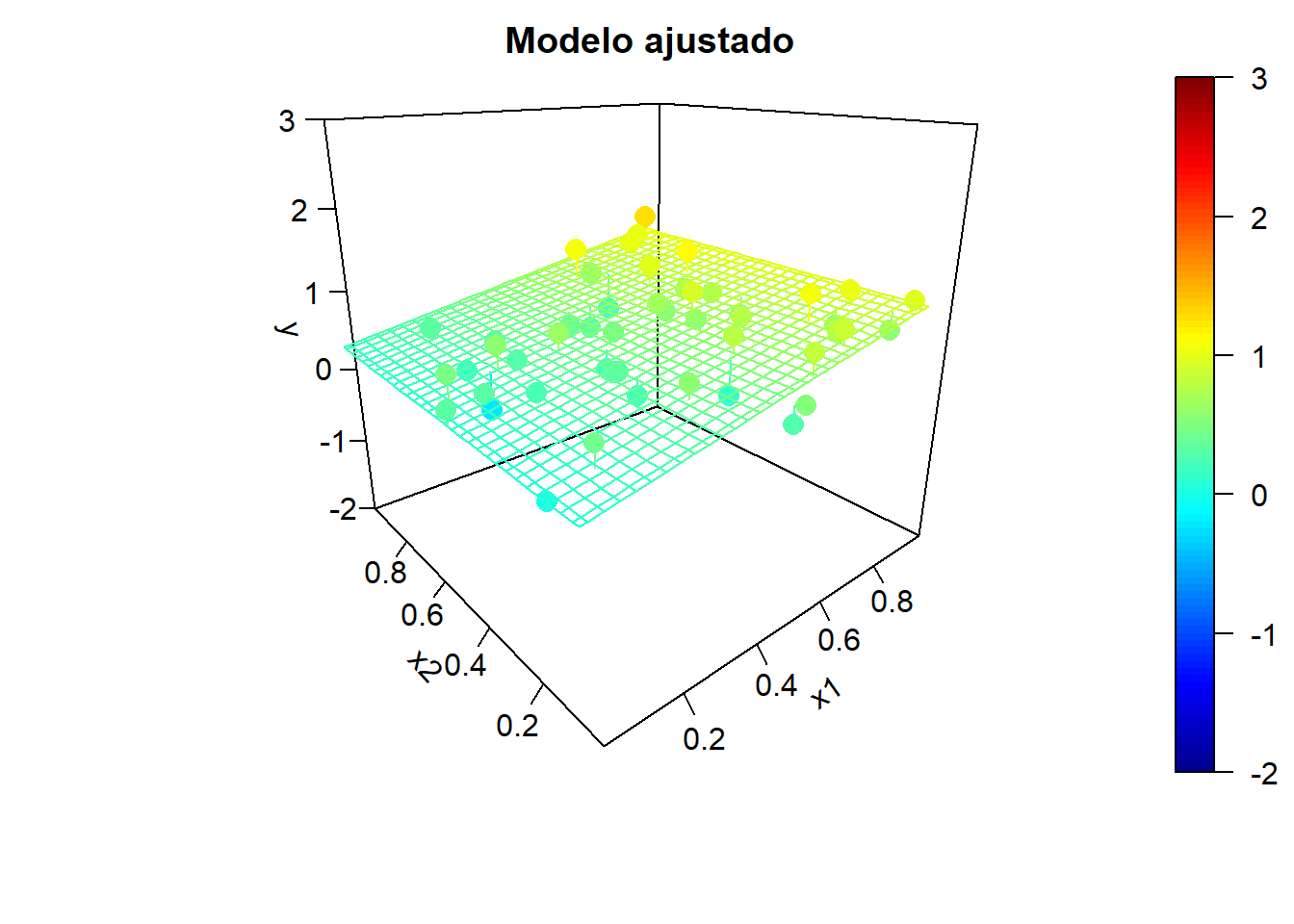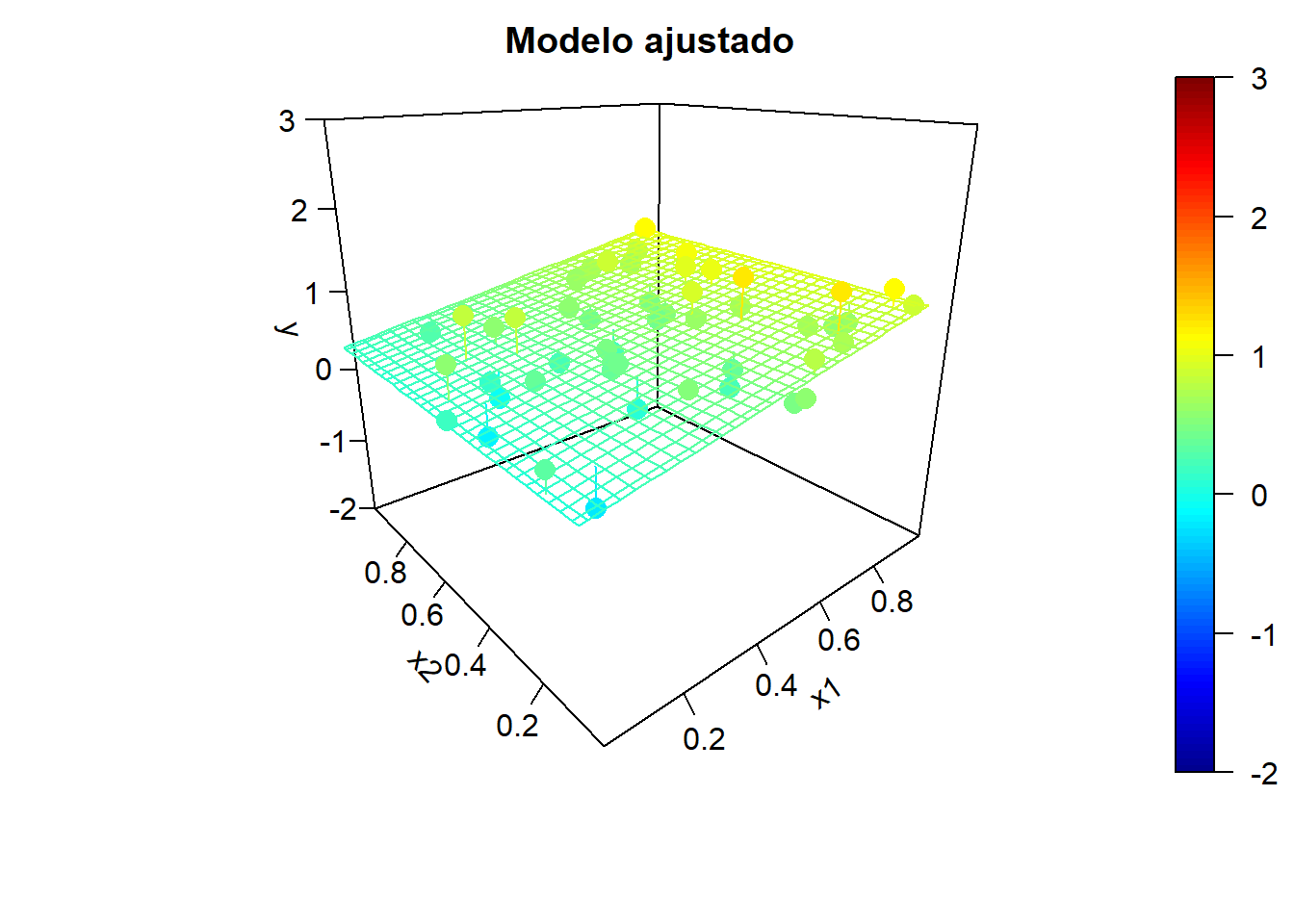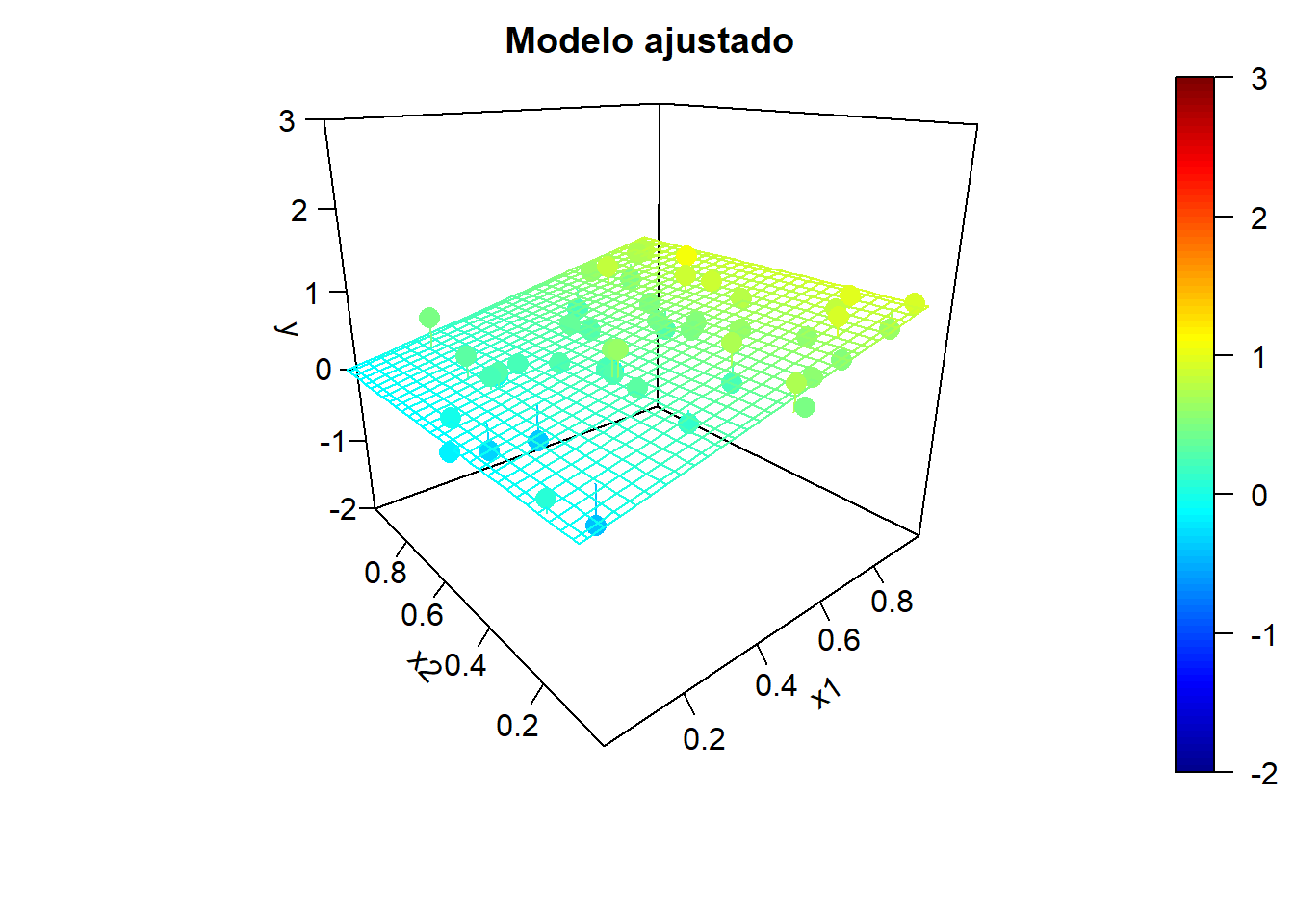
Ejemplo de simulaciones bajo independencia y correspondientes modelos ajustados.

Figura 6.6: Ejemplo de simulaciones bajo independencia y correspondientes modelos ajustados.

Por ejemplo, en el último ajuste obtendríamos:

summary(fit2)
## 
## Call:
## lm(formula = y ~ x1 + x2)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.45800 -0.08645  0.00452  0.15402  0.33662 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -0.22365    0.08515  -2.627   0.0116 *  
## x1           1.04125    0.11044   9.428 2.07e-12 ***
## x2           0.22334    0.10212   2.187   0.0337 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2105 on 47 degrees of freedom
## Multiple R-squared:  0.6648, Adjusted R-squared:  0.6505 
## F-statistic:  46.6 on 2 and 47 DF,  p-value: 7.016e-12

En la práctica, para la detección de colinealidad, se puede emplear la función vif() del paquete car para calcular los factores de inflación de varianza para las variables del modelo. Por ejemplo, en los últimos ajustes obtendríamos:

library(car)
vif(fit)
##       x1       x2 
## 107.0814 107.0814
vif(fit2) 
##       x1       x2 
## 1.000139 1.000139

La idea de este estadístico es que la varianza de la estimación del efecto en regresión simple (efecto global) es menor que en regresión múltiple (efecto parcial). El factor de inflación de la varianza mide el incremento debido a la colinealidad. Valores grandes, por ejemplo > 10, indican la posible presencia de colinealidad.

Las tolerancias, proporciones de variabilidad no explicada por las demás covariables, se pueden calcular con 1/vif(modelo). Por ejemplo, los coeficientes de tolerancia de los últimos ajustes serían:

1/vif(fit)
##          x1          x2 
## 0.009338689 0.009338689
1/vif(fit2) 
##        x1        x2 
## 0.9998606 0.9998606

Como ya se comentó en la Sección 1.4, el problema de la colinealidad se agrava al aumentar el número de dimensiones (la maldición de la dimensionalidad). Hay que tener en cuenta también que, además de la dificultad para interpretar el efecto de los predictores, va a resultar más difícil determinar que variables son de interés para predecir la respuesta (i.e. no son ruido). Debido a la aleatoriedad, predictores que realmente no están relacionados con la respuesta pueden ser tenidos en cuenta por el modelo con mayor facilidad, especialmente si se recurre a los contrastes tradicionales para determinar si tienen un efecto significativo.