Chi-squared goodness-of-fit test for continuous data

Source: R/test.R

Performs the chi-squared goodness-of-fit test for a continuous distribution by grouping data into bins (also called intervals, classes or cells) with equal probabilities under the null hypothesis.

chisq.cont.test(
  x,
  distribution = "norm",
  nclass = floor(length(x)/5),
  output = TRUE,
  nestpar = 0,
  ...
)

Arguments

x

numeric vector containing the observed values.

distribution

character string naming a continuous distribution, such as "norm" or "unif" (the cumulative distribution p<distribution>() and quantile q<distribution>() functions must exist).

nclass

number of bins.

output

logical; if TRUE an histogram is plotted and a table with the results for each class is printed.

nestpar

number of estimated parameters (composite null hypothesis).

...

parameters of the distribution (specified by distribution).

Value

A list with class "htest" containing the following components:

statistic

the value the chi-squared test statistic.

parameter

the degrees of freedom of the approximate chi-squared distribution of the test statistic.

p.value

the p-value for the test.

method

a character string indicating the type of test performed.

data.name

a character string with the actual x argument name.

classes

a character vector with the class labels.

observed

the observed counts.

expected

the expected counts under the null hypothesis.

residuals

the Pearson residuals, (observed - expected) / sqrt(expected).

Examples

nx <- 30
x <- rnorm(nx)
chisq.cont.test(x, distribution = "norm", nestpar = 2,
                mean = mean(x), sd = sqrt((nx - 1) / nx) * sd(x))

#> 
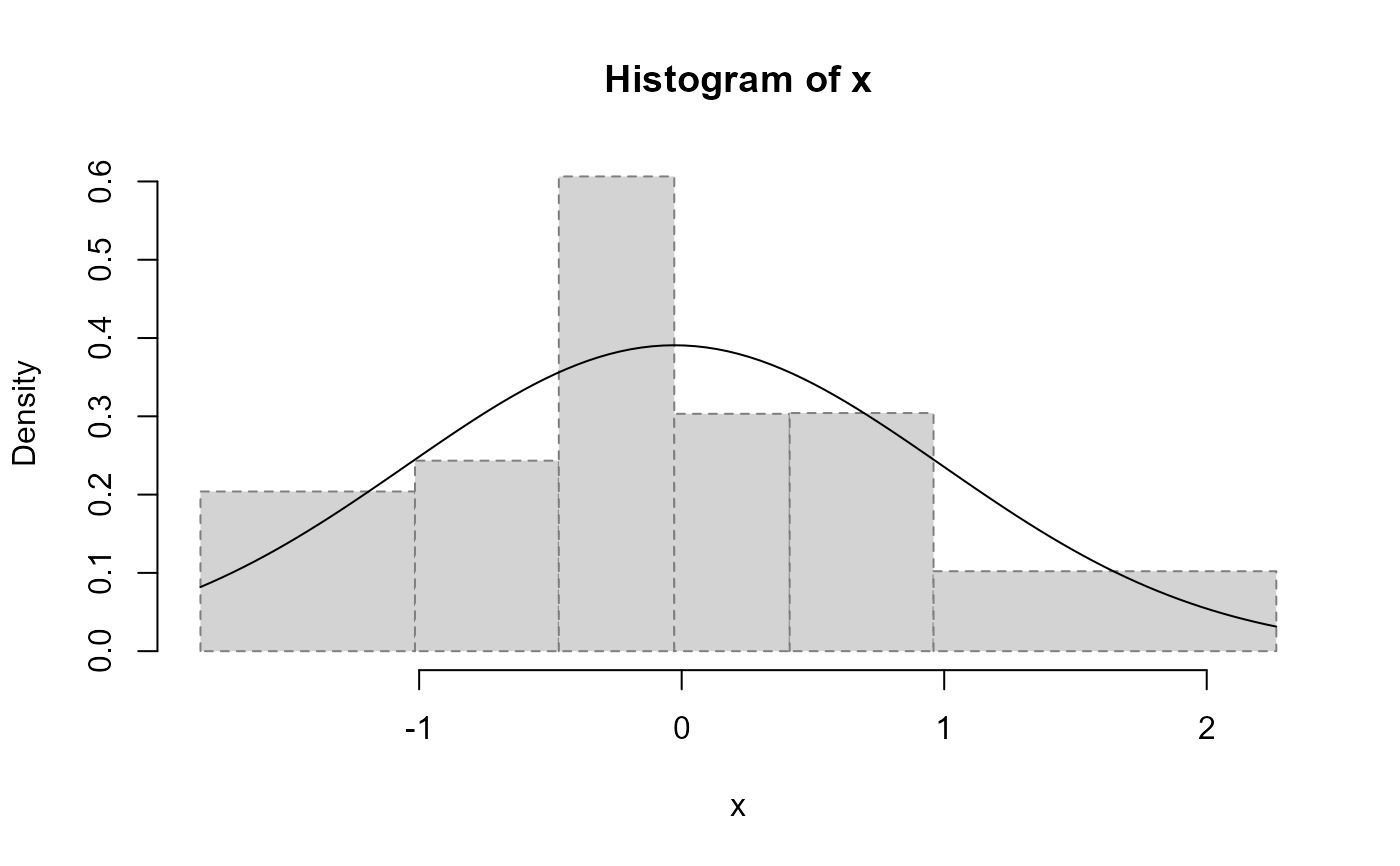#> Pearson's Chi-squared test table
#>                     classes observed expected  residuals
#> 1 (-1.83297059,-1.01588461]        5        5  0.0000000
#> 2 (-1.01588461,-0.46797368]        4        5 -0.4472136
#> 3 (-0.46797368,-0.02824437]        8        5  1.3416408
#> 4 (-0.02824437, 0.41148493]        4        5 -0.4472136
#> 5 ( 0.41148493, 0.95939586]        5        5  0.0000000
#> 6 ( 0.95939586, 2.26507865]        4        5 -0.4472136
#> 
#> 	Pearson's Chi-squared test
#> 
#> data:  x
#> X-squared = 2.4, df = 3, p-value = 0.4936
#>