Linear binning

Source: R/bin.data.R

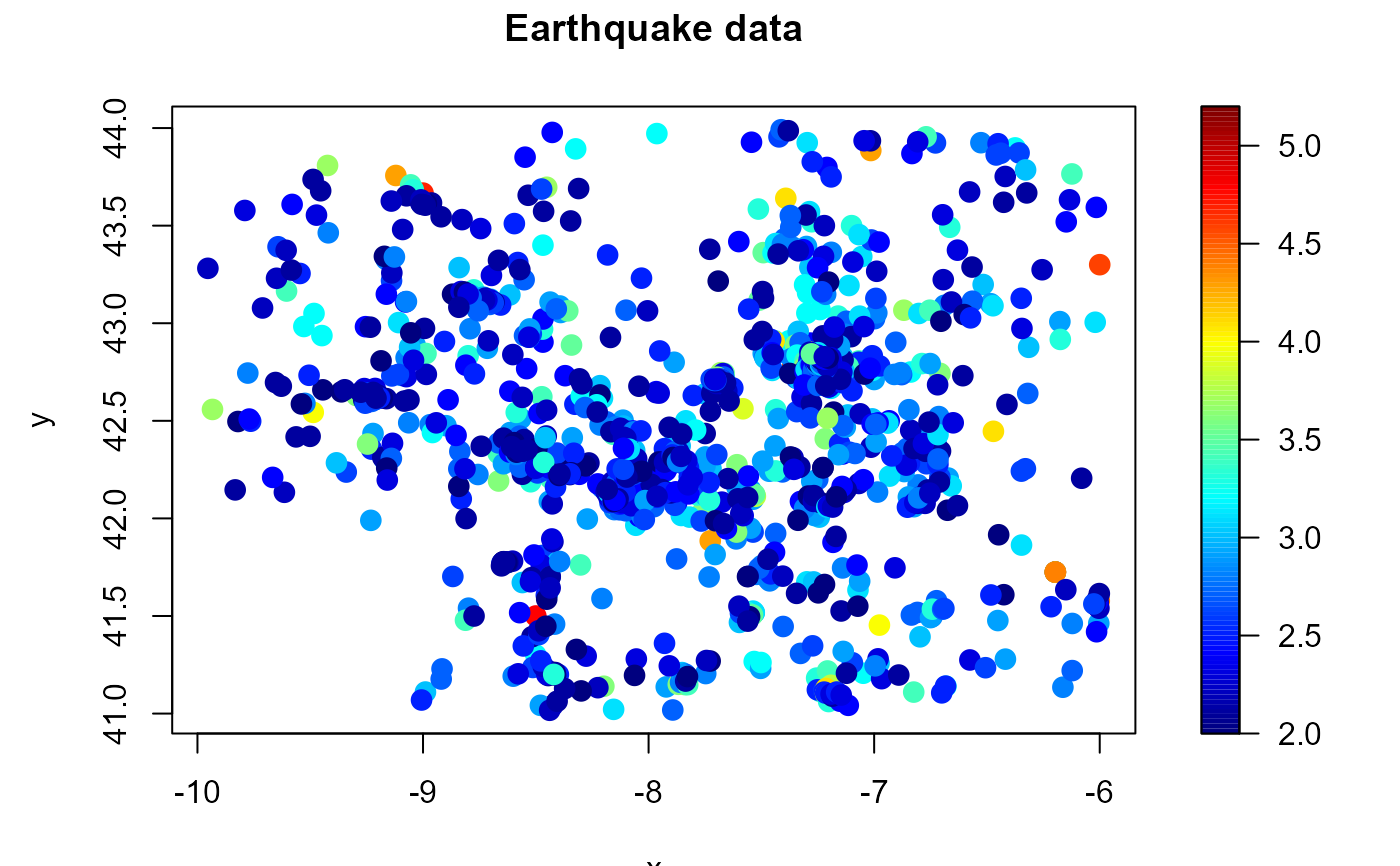
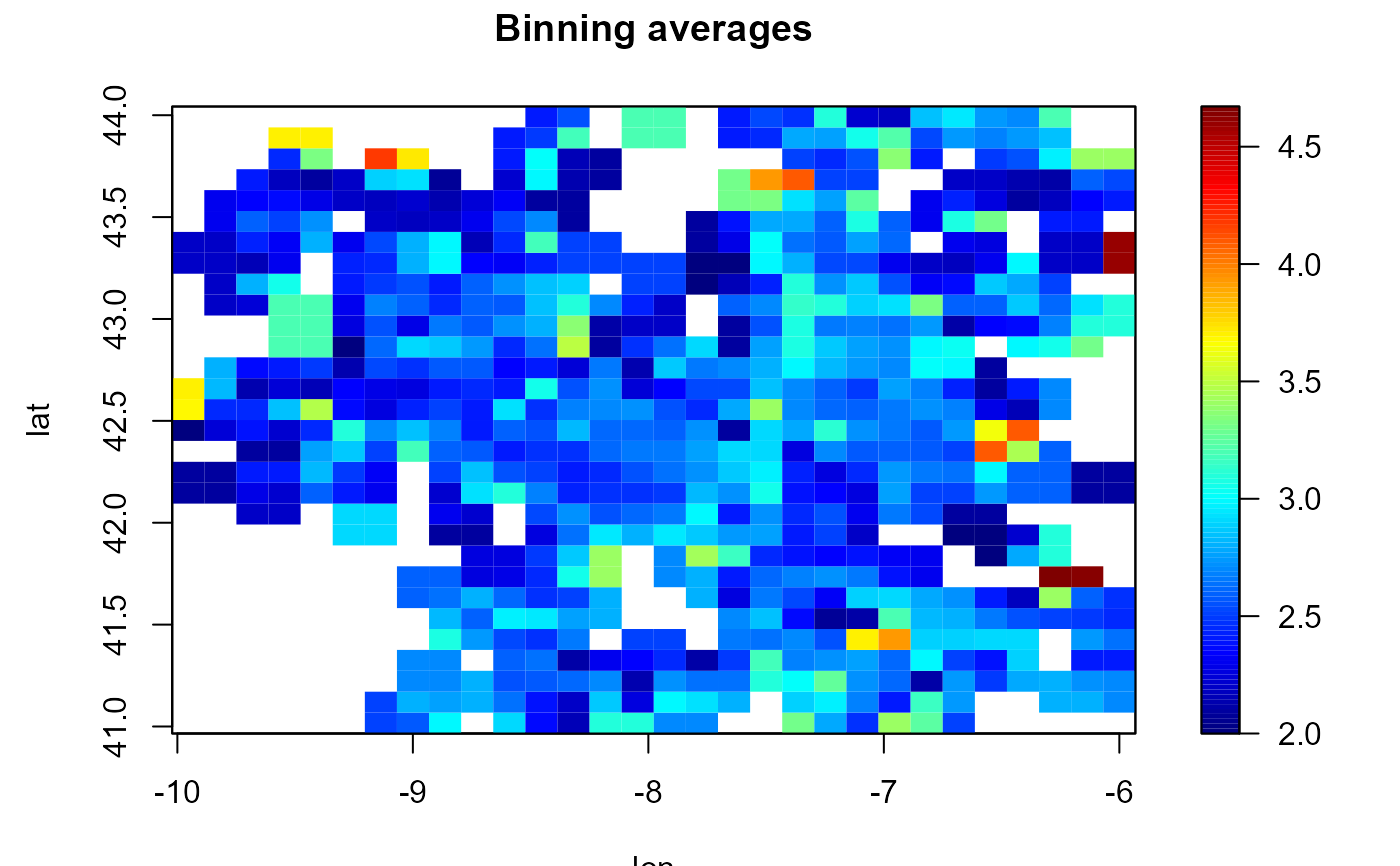
Discretizes the data into a regular grid (computes a binned approximation) using the simple and linear multivariate binning techniques described in Wand (1994).

binning(
  x,
  y = NULL,
  nbin = NULL,
  type = c("linear", "simple"),
  set.NA = FALSE,
  window = NULL,
  ...
)

as.bin.data(object, ...)

# S3 method for class 'data.grid'
as.bin.data(object, data.ind = 1, weights.ind = NULL, ...)

# S3 method for class 'bin.data'
as.bin.data(object, ...)

# S3 method for class 'SpatialGridDataFrame'
as.bin.data(object, data.ind = 1, weights.ind = NULL, ...)

Arguments

x

vector or matrix of covariates (e.g. spatial coordinates). Columns correspond with covariates (coordinate dimension) and rows with data.

y

vector of data (response variable).

nbin

vector with the number of bins on each dimension.

type

character, binning method: "linear" (default) or "simple".

set.NA

logical. If TRUE, sets the bin averages corresponding to cells without data to NA.

window

spatial window (values outside this window will be masked), currently an sp-object of class extending SpatialPolygons.

...

further arguments passed to mask.bin.data().

object

(gridded data) used to select a method.

data.ind

integer (or character) with the index (or name) of the component containing the bin averages.

weights.ind

integer (or character) with the index (or name) of the component containing the bin counts/weights (if not specified, they are set to as.numeric( is.finite( object[[data.ind]] ))).

Value

If y != NULL, an S3 object of class bin.data (gridded binned data; extends bin.den) is returned. A data.grid object with the following 4 components:

biny

vector or array (dimension nbin) with the bin averages.

binw

vector or array (dimension nbin) with the bin counts (weights).

grid

a grid.par-class object with the grid parameters.

data

a list with 3 components:

  • x argument x.

  • y argument y.

  • med (weighted) mean of the (binned) data.

If y == NULL, bin.den is called and a bin.den-class object is returned.

Details

If parameter nbin is not specified is set to pmax(25, rule.binning(x)).

Setting set.NA = TRUE (equivalent to biny[binw == 0] <- NA) may be useful for plotting the binned averages $biny (the hat matrix should be handled with care when using locpol).

References

Wand M.P. (1994) Fast Computation of Multivariate Kernel Estimators. Journal of Computational and Graphical Statistics, 3, 433-445.

See also

data.grid, locpol, bin.den, h.cv.

Examples

with(earthquakes, spoints(lon, lat, mag, main = "Earthquake data"))


bin <- binning(earthquakes[, c("lon", "lat")], earthquakes$mag, nbin = c(30,30), set.NA = TRUE)

simage(bin, main = "Binning averages", reset = FALSE)
with(earthquakes, points(lon, lat, pch = 20))