En esta presentación para el X Seminario Internacional SEE, se pretende proporcionar una introducción a la Geoestadística No Paramétrica desde un punto de vista aplicado, empleando el paquete npsp (Nonparametric spatial statistics) del entorno estadístico R.
Para los detalles teóricos se puede consultar, además de las referencias incluidas al final de este trabajo, la documentación en la web del paquete o la tesis doctoral:
Castillo-Páez, S. (2017). Aportaciones a la Geoestadística no paramétrica. Tesis doctoral (UVigo, España). Directores: Pilar García-Soidán, Rubén Fernández-Casal.
El paquete npsp implementa métodos no paramétricos para la inferencia en procesos geoestadísticos multidimensionales, evitando los problemas de mala especificación que pueden surgir con la aproximación tradicional al utilizar modelos paramétricos.
El proceso espacial puede ser estacionario o mostrar una tendencia no constante. La estimación conjunta de la tendencia y el semivariograma puede realizarse de forma automática, utilizando la función np.fitgeo(), o estimando las distintas componentes por pasos.
library(npsp) Package npsp: Nonparametric Spatial Statistics,
version 0.7-8 (built on 2021-05-10).
Copyright (C) R. Fernandez-Casal 2012-2021.
Type `help(npsp)` for an overview of the package or
visit https://rubenfcasal.github.io/npsp.Introducción
Nos centraremos en el caso de procesos espaciales \(\left\lbrace Y(\mathbf{x}), \mathbf{x} \in D\subset \mathbb{R}^{d} \right\rbrace\), con dominio \(D\) continuo fijo: procesos geoestadísticos1.
Normalmente sólo se observa un conjunto de valores \(\left\{ y(\mathbf{x}_{1}),\ldots,y(\mathbf{x}_{n})\right\}\) (una realización parcial).
Por ejemplo podemos utilizar la función (genérica) spoints() para representar los datos (genera un gráfico de dispersión de las posiciones con una escala de color para la respuesta). En este trabajo utilizaremos como ejemplo dos conjuntos de datos suministrado con el paquete npsp:
aquifer: nivel del agua subterránea (pies sobre el nivel del mar) en 85 localizaciones del acuífero Wolfcamp.x <- aquifer[,1:2] # coordenadas espaciales y <- aquifer$head/100 # respuesta (en cientos de pies) spoints(x$lon, x$lat, y, main = "Datos del acuífero Wolfcamp", xlab = "Longitud", ylab = "Latitud", legend.lab = "nivel piezométrico (cientos de pies)")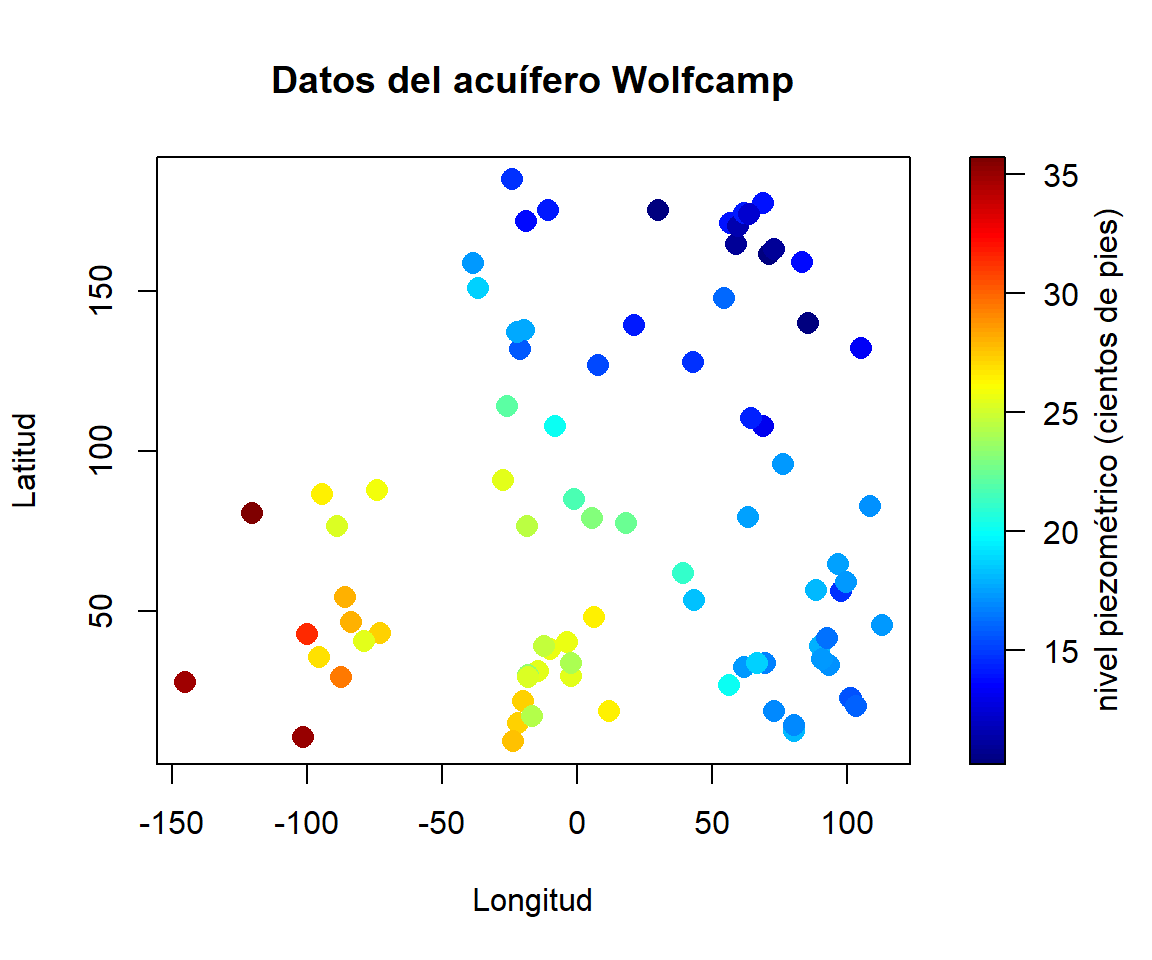
precipitation: total de precipitaciones (raíz cuadrada de pulgadas de lluvia) durante marzo de 2016 registradas en 1053 localidades de la parte continental de Estados Unidos (objeto de clasesp::SpatialGridDataFrame).library(sp) spoints(precipitation, asp = 1)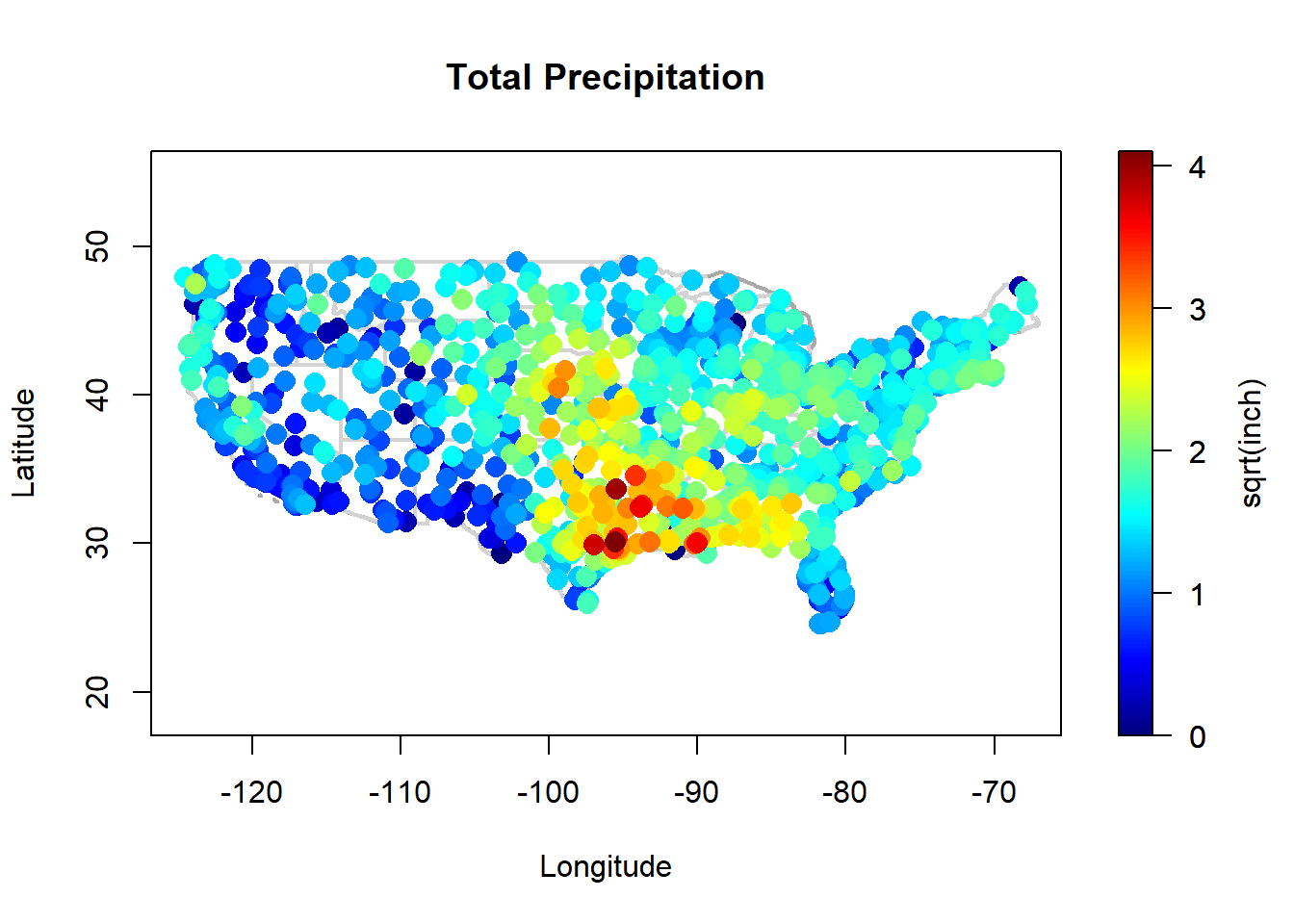
attr <- attributes(precipitation) border <- attr$border interior <- attr$interior
Modelo general
Supondremos que el proceso se descompone en variabilidad de gran escala y variabilidad de pequeña escala: \[Y(\mathbf{x})=\mu(\mathbf{x})+\varepsilon(\mathbf{x}),\] donde:
\(\mu(\cdot)\) es la tendencia (función de regresión, determinística).
\(\varepsilon(\cdot)\) es un proceso de error estacionario de segundo orden, de media cero y covariograma: \[C(\mathbf{u}) = Cov(\varepsilon(\mathbf{x}), \varepsilon(\mathbf{x}+\mathbf{u} ))\] (varianza \(\sigma^2 = C(\mathbf{0})\)).
La dependencia espacial se modela normalmente a través del variograma: \[2\gamma(\mathbf{u}) = Var(\varepsilon \left( \mathbf{x}\right) -\varepsilon \left(\mathbf{x}+\mathbf{u}\right) ),\] verificando \(\gamma(\mathbf{u}) = C(0) - C(\mathbf{u})\).
Se podrían considerar un modelo aún más general heterocedástico (ver Fernández-Casal et al., 2017).
A partir de los valores observados \(\mathbf{Y}=(Y(\mathbf{x}_1),\ldots,Y(\mathbf{x}_n))^{t}\), los objetivos suelen ser:
Obtener predicciones (kriging): \(\hat{Y}(\mathbf{x}_0)\).
Realizar inferencias (estimación, contrastes) sobre las componentes del modelo \(\hat{\mu}(\cdot)\), \(\hat{\gamma}(\cdot)\).
Obtención de mapas de riesgo \(P({Y}(\mathbf{x}_0)\geq c)\).
Realizar inferencias sobre la distribución (condicional) de la respuesta en nuevas localizaciones, …
En cualquier caso el primer paso consiste en estimar las componentes del modelo: la tendencia \(\mu(\mathbf{x})\) y el semivariograma \(\gamma(\mathbf{h})\).
Aproximación tradicional
Hay una gran cantidad de paquetes disponibles en R para el análisis de datos geoestadístico empleando la metodología tradicional (ver CRAN Task View: Analysis of Spatial Data).
Por ejemplo, en el post Introducción a la Geoestadística con geoR
se ilustran algunas de las capacidades del paquete geoR.
Otra alternativa muy utilizada es el paquete gstat.
En la aproximación clásica (paramétrica) habitualmente se siguen los siguientes pasos:
Análisis descriptivo y formulación de un modelo paramétrico (inicial).
Estimación de los parámetros del modelo:
Estimar y eliminar la tendencia.
Ajustar un modelo de variograma a los residuos.
Validación del modelo o reformulación del mismo.
Empleo del modelo aceptado.
Por ejemplo, en el primer paso, los gráficos de dispersión de los datos frente a las coordenadas nos pueden ayudar a determinar si hay una tendencia (función scattersplot()).
En el caso de los datos del acuífero Wolfcamp, el tamaño muestral es pequeño y un modelo lineal para la tendencia parece ser adecuado, por lo que podría ser preferible emplear métodos paramétricos.
scattersplot(x, y, main = "Wolfcamp aquifer data",
xlab = 'Longitude', ylab ='Latitude',
zlab = 'piezometric-head', col = jet.colors(128))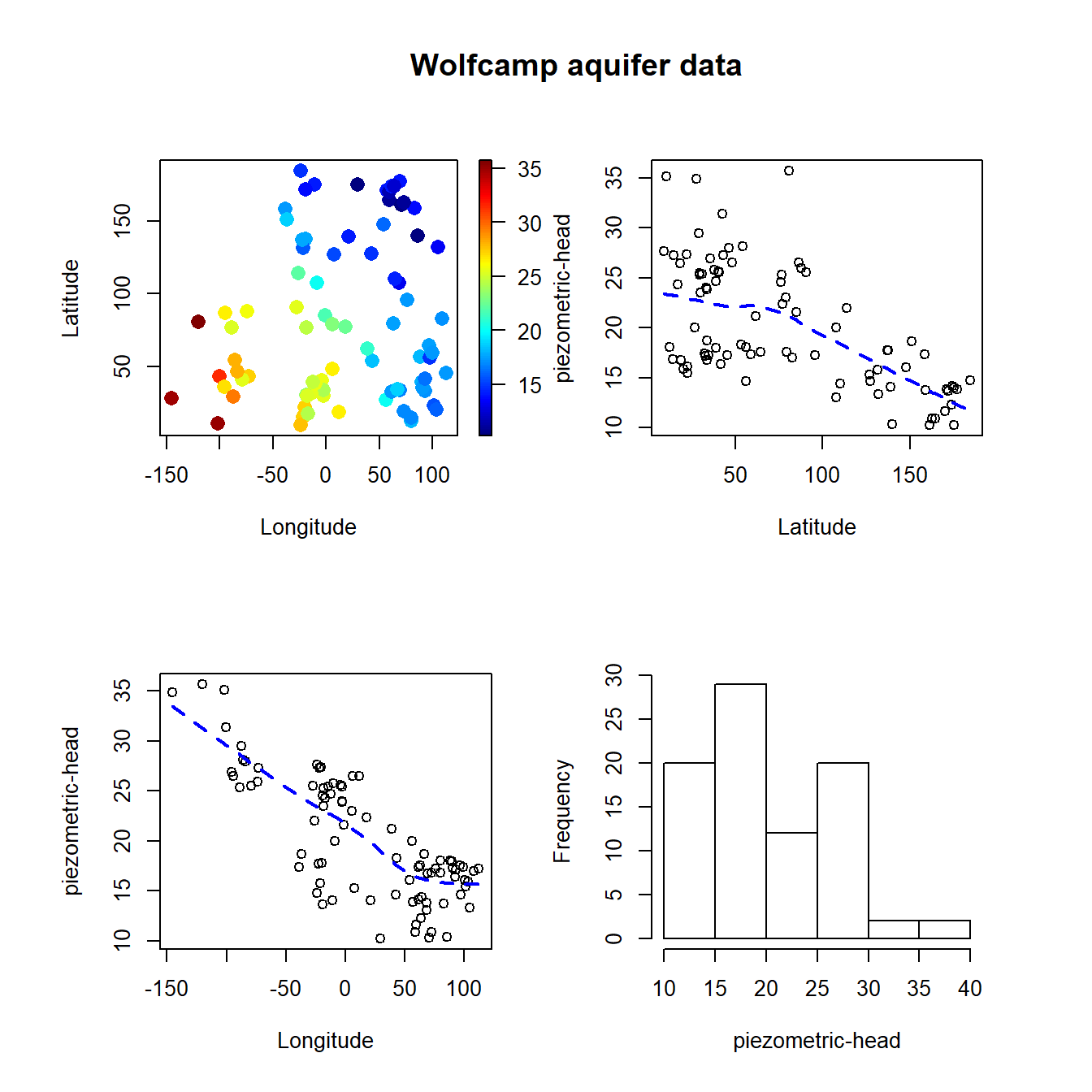
Sin embargo, en el caso de los datos de precipitaciones puede resultar mucho más complicado obtener un modelo paramétrico adecuado para la tendencia (habría que considerar un modelo no lineal y seguramente el ajuste no será totalmente satisfactorio considerando únicamente las posiciones espaciales como variables explicativas):
scattersplot(precipitation)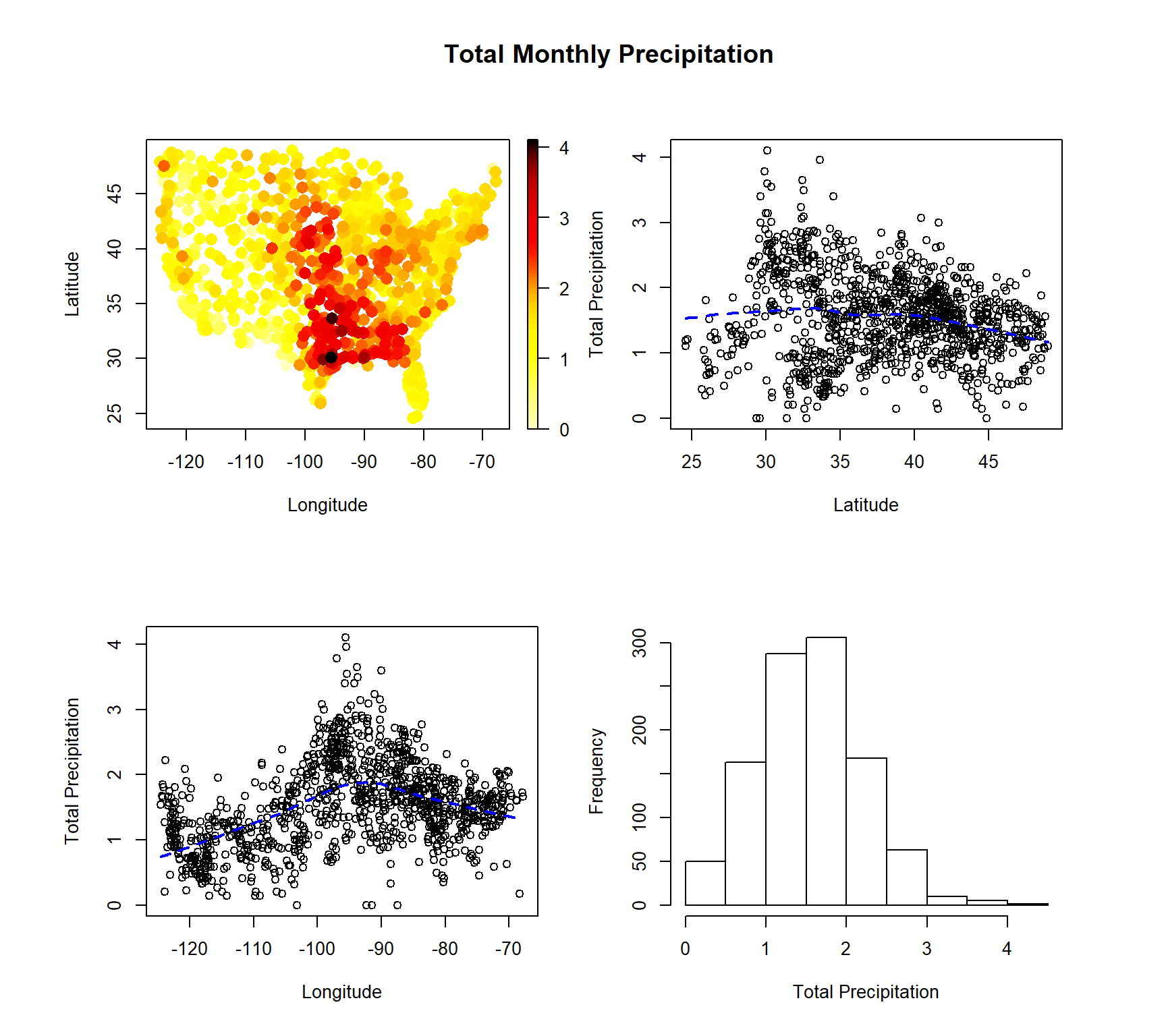
El mismo problema puede surgir en el modelado de la dependencia (además, la variabilidad no capturada en la variación de gran escala debería ser asumida por la variación de pequeña escala).
Geoestadística no paramétrica
En ciertos casos puede ser preferible emplear un modelo no paramétrico: no se supone ninguna forma concreta para \(\mu(\mathbf{\cdot})\) y \(\gamma(\mathbf{\cdot})\) (funciones suaves).
Evitan problemas debidos a una mala especificación del modelo.
Más fáciles de automatizar.
Resultan también de utilidad en inferencia paramétrica.
Aunque hay una gran cantidad de paquetes de R con herramientas
de utilidad en geoestadística (geoR, gstat, fields, …)
o en estadística no paramétrica (mgcv, np, KernSmooth, sm, …),
la mayoría presentan una funcionalidad muy limitada para estadística espacial
no paramétrica o resulta difícil emplearlos para implementar nuevos métodos
(además de otras limitaciones, como su eficiencia computacional o el número de dimensiones que soportan).
Por este motivo se decidió desarrollar el paquete
npsp:
Github (versión de desarrollo): http://github.com/rubenfcasal/npsp
Actualmente la última versión solo está disponible en Github. Para instalarla (a partir del código) puede ser de utilidad este post.
La idea es:
Proporcionar un entorno homogéneo para la estimación polinómica local multidimensional (tendencia, variograma, densidad, …), especialmente para el caso de procesos espaciales (y espacio-temporales).
Trata de minimizar el tiempo de computación y los requerimientos de memoria.
Emplear clases y métodos S3 sencillos (que permitan interactuar con las clases S4 para datos espaciales del paquete
spy las nuevas clases S3 del paquetesf; ver npsp/inst/locpol_classes.pdf).Robusto y que facilite la implementación de nuevos métodos.
Estimación de la tendencia
Como ya se comentó, se emplea regresión polinómica local para la estimación de la tendencia (e.g. Fan and Gijbels, 1996). El estimador \(\hat{\mu}_{\mathbf{H}}(\mathbf{x})\) se obtiene aplicando un suavizado polinómico a los datos \(\{(\mathbf{x}_{i},Y(\mathbf{x}_{i})):i=1,\ldots,n\}\).
En el caso univariante, para cada \(x_{0}\) se ajusta un polinomio: \[\beta_{0}+\beta_{1}\left(x - x_{0}\right) + \cdots + \beta_{p}\left( x-x_{0}\right)^{p}\] por mínimos cuadrados ponderados, con pesos \(w_{i} = \frac{1}{h}K\left(\frac{x-x_{0}}{h}\right)\).
La estimación en \(x_{0}\) es \(\hat{\mu}_{h}(x_{0})=\hat{\beta}_{0}\).
Podemos obtener también estimaciones de las derivadas: \(\widehat{\mu_{h}^{r)}}(x_{0}) = r!\hat{\beta}_{r}\).
Habitualmente se considera:
\(p=0\): Estimador Nadaraya-Watson.
\(p=1\): Estimador lineal local.
La ventana \(h\) controla el grado de suavizado (el tamaño del vecindario local empleado en los ajustes). Puede ser de utilidad esta aplicación shiny para ilustrar este método (ver p.e. García-Portugués, 2021, Sección 4.1.2; Fernández-Casal y Costa, 2021, Sección 7.1.2).
El caso multivariante es análogo. La estimación lineal local multivariante \(\hat{\mu}_{\mathbf{H}}(\mathbf{x})=\hat{\beta}_{0}\) se obtiene al minimizar: \[\min_{\beta_{0},\boldsymbol{\beta}_{1}}\sum_{i=1}^{n} \left( Y(\mathbf{x}_{i})-\beta_{0}-{\boldsymbol{\beta}}_{1}^{t} (\mathbf{x}_{i}-\mathbf{x})\right)^{2} K_{\mathbf{H}}(\mathbf{x}_{i}-\mathbf{x}),\] donde:
\(\mathbf{H}\) es la matriz de ventanas \(d\times d\) (simétrica no singular; controla la forma y el tamaño del vecindario).
\(K_{\mathbf{H}}(\mathbf{u})=\left\vert \mathbf{H}\right\vert ^{-1}K(\mathbf{H}^{-1}\mathbf{u})\) y \(K\) núcleo multivariante.
De esta forma, las estimaciones en las posiciones de los datos se pueden expresar como una transformación lineal de las observaciones: \[\hat{\boldsymbol{\mu}} = \mathbf{SY},\] siendo \(\mathbf{S}\) la denominada matriz de suavizado (este tipo de métodos también se denominan suavizadores lineales). Esta matriz resulta de utilidad, entre otras cosas, para la selección de la ventana y la estimación de la dependencia.
La estimación polinómica local está implementada en la función genérica
locpol():
Emplea una matriz de ventanas completa y un núcleo triweight para el cálculo de los pesos.
Permite calcular eficientemente la matriz de suavizado \(\mathbf{S}\).
Código optimizado para minimizar el tiempo de computación y los requerimientos de memoria (especialmente para validación cruzada, estimación del variograma, …). Los cálculos se realizan en FORTRAN empleando la librería LAPACK.
Por ejemplo, en el caso de los datos de precipitación, podemos obtener la estimación de la tendencia mediante los comandos:
x <- sp::coordinates(precipitation)
y <- precipitation$y
lp <- locpol(x, y, nbin = c(120, 120), h = diag(c(5, 5)))Podemos representar las estimaciones de la tendencia con la función simage() (o spersp()).
Además, en este caso enmascaramos previamente las estimaciones fuera de la parte continental de EE.UU..
lp <- mask(lp, window = border, warn = FALSE)
# Representar
slim <- range(y)
col <- jet.colors(256)
simage(lp, slim = slim, main = "Trend estimates",
col = col, xlab = "Longitude", ylab = "Latitude", asp = 1)
plot(border, border = "darkgray", lwd = 2, add = TRUE)
plot(interior, border = "lightgray", lwd = 1, add = TRUE)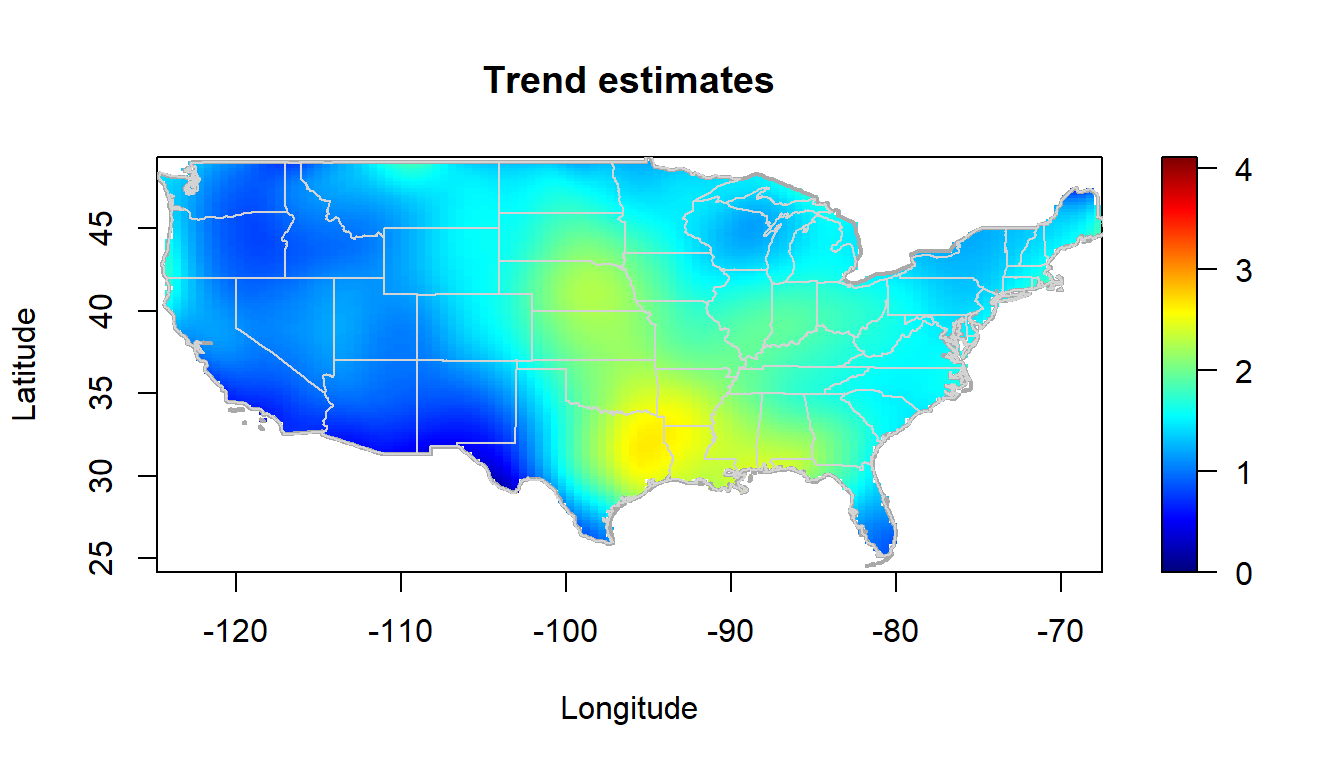
Para acelerar los cálculos se emplea binning lineal (e.g. Wand and Jones, 1995), el resultado final es una rejilla. Para obtener estimaciones en otras posiciones se puede emplear las funciones predict() e interp() para interpolar2.
Por ejemplo, en lugar del código anterior podríamos emplear (seleccionando de paso una ventana más pequeña para comparar el resultado):
bin <- binning(x, y, nbin = c(120, 120), window = border)
# lp <- locpol(bin, h = diag(c(5, 5)))
lp2 <- locpol(bin, h = diag(c(2, 2)))
simage(lp2, slim = slim, main = "Trend estimates",
col = col, xlab = "Longitude", ylab = "Latitude", asp = 1)
plot(border, border = "darkgray", lwd = 2, add = TRUE)
plot(interior, border = "lightgray", lwd = 1, add = TRUE)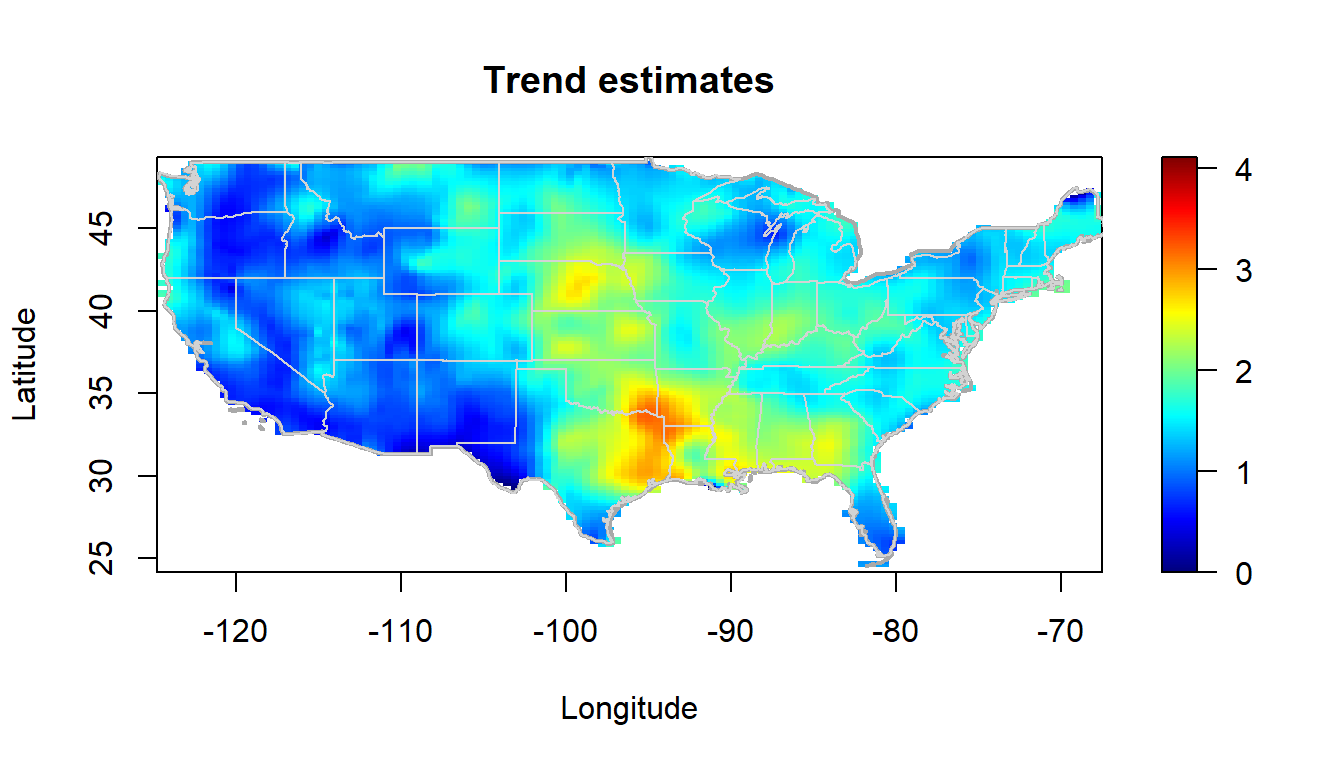
Normalmente se emplearan dos rejillas, una de baja resolución para acelerar los cálculos durante el proceso de modelado (selección de la ventana, cálculos intermedios, …) y otra con la resolución deseada para obtener los resultados finales.
Selección de la ventana
La estimación de la tendencia depende de forma crítica de la matriz ventanas \(H\). Una ventana pequeña dará lugar a estimaciones poco suaves (infrasuavizado), mientras una ventana grande suavizará en exceso los datos (sobresuavizado). Aunque puede elegirse de forma subjetiva (mediante prueba y error), puede ser de utilidad emplear métodos de selección automáticos.
En el caso de datos dependientes, los criterios tradicionales de selección de la ventana (diseñados para datos independientes), como la validación cruzada tradicional (LOOCV) o la validación cruzada generalizada (GCV; Craven y Wahba, 1978), tienden a infrasuavizar la estimación de la tendencia (e.g. Opsomer et al., 2001).
El criterio de validación cruzada modificado (MCV), propuesto en (Chu y Marron, 1991) para series temporales, puede adaptarse a datos espaciales, ignorando las observaciones en un vecindario \(N(i)\) de \(\mathbf{x}_{i}\) (el criterio LOOCV tradicional es un caso particular con \(N(i)=\left\lbrace \mathbf{x}_{i} \right\rbrace\)).
En la práctica, se puede seleccionar la ventana empleando la función genérica h.cv() (que por defecto emplea el criterio MCV y el método "L-BFGS-B" de la función optim()3):
bin <- binning(x, y, window = border)
lp0.h <- h.cv(bin)$h
lp0 <- locpol(bin, h = lp0.h, hat.bin = TRUE) Adicionalmente se pueden emplear otros criterios que tienen en cuenta la dependencia espacial, como la validación cruzada generalizada con corrección de sesgo para dependencia (CGCV), propuesta en Francisco-Fernandez y Opsomer (2005).
Para utilizar este criterio en la práctica (calculando previamente la matriz de suavizado y estableciendo posteriormente objective = "GCV" y cov.bin en h.cv()) se requiere previamente una estimación del variograma (este problema circular se tratará más adelante en la Sección Modelado automático).
Estimación del variograma
Al igual que en la geoestadística paramétrica tradicional, la estimación se realiza en dos pasos, en primer lugar se obtiene una estimación piloto del variograma y posteriormente se ajusta un modelo válido.
Si la media se supone constante (proceso estacionario), se puede obtener una estimación piloto lineal local \(\hat\gamma(\mathbf{u})\) mediante el suavizado de las semivarianzas \(\left(\mathbf{x}_{i}-\mathbf{x}_{j},(Y(\mathbf{x}_i)- Y(\mathbf{x}_j))^2/2 \right)\). La correspondiente ventana puede seleccionarse por ejemplo minimizando el error cuadrático relativo de validación cruzada.
En el caso general, cuando la tendencia no es constante, la aproximación habitual consiste en eliminar la tendencia y estimar el variograma a partir de los residuos \(\mathbf{r}=\mathbf{Y}-\mathbf{SY}\). Sin embargo, la variabilidad de los residuos puede ser muy diferente a la de los verdaderos errores (ver, por ejemplo, Cressie, 1993, sección 3.4.3, para el caso de una tendencia lineal). Como el sesgo debido al uso directo de los residuos en la estimación del variograma puede tener un impacto significativo en la inferencia, se puede considerar una aproximación similar a la descrita en Fernández-Casal y Francisco-Fernández (2014).
En la práctica, las estimaciones piloto del variograma pueden calcularse con las funciones np.svar() y np.svariso.corr().
La función genérica h.cv() puede utilizarse para seleccionar la ventana correspondiente4.
Actualmente en el paquete npsp solo está implementado el caso isotrópico.
svar.bin <- svariso(x, residuals(lp0), nlags = 60, maxlag = 20)
svar.h <- h.cv(svar.bin)$h
svar.np <- np.svar(svar.bin, h = svar.h)
svar.np2 <- np.svariso.corr(lp0, nlags = 60, maxlag = 20,
h = svar.h, plot = FALSE) Los estimadores piloto no verifican las propiedades de un variograma (condicionalmente semidefinidos negativos) y no pueden ser usados en predicción espacial (kriging). Para resolver este problema se puede ajustar un modelo no paramétrico de Shapiro-Botha (Shapiro and Botha, 1991) empleando mínimos cuadrados ponderados (mediante programación cuadrática, lo que evita problemas de mínimos locales).
En la practica se pueden ajustar este tipo de modelos empleando la función fitsvar.sb.iso()5.
svm0 <- fitsvar.sb.iso(svar.np, dk = 0)
svm1 <- fitsvar.sb.iso(svar.np2, dk = 0)
# plot...
plot(svm1, main = "Nonparametric bias-corrected semivariogram\nand fitted models",
legend = FALSE, xlim = c(0,max(coords(svar.np2))),
ylim = c(0,max(svar.np2$biny, na.rm = TRUE)))
plot(svm0, lwd = c(1, 1), add = TRUE)
plot(svar.np, type = "p", pch = 2, add = TRUE)
# abline(h = c(svm1$nugget, svm1$sill), lty = 3)
# abline(v = 0, lty = 3)
legend("bottomright", legend = c("corrected", 'biased'),
lty = c(1, 1), pch = c(1, 2), lwd = c(1, 1))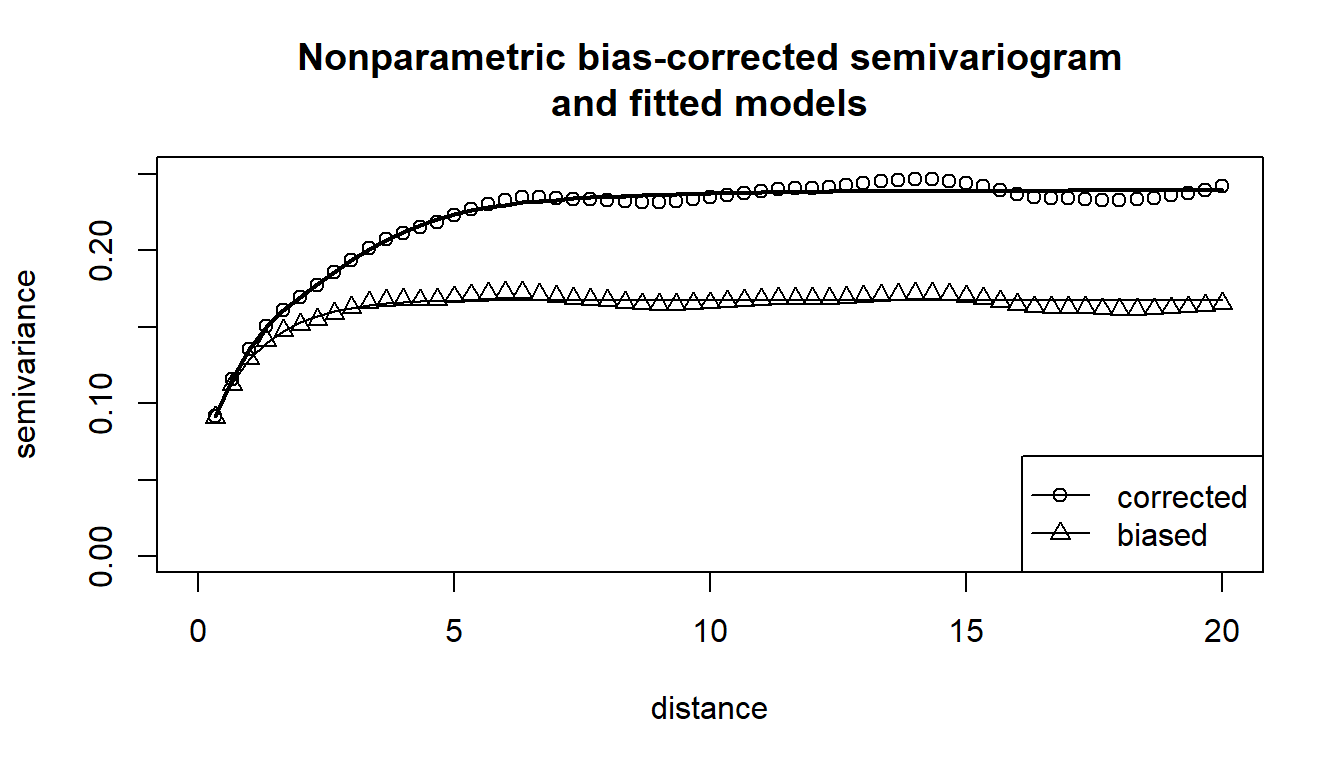
Empleando el modelo ajustado de variograma se podría seleccionar una nueva ventana “óptima” para la estimación de la tendencia. Aunque si cambia la estimación de la tendencia también habría que volver a estimar el variograma (si se modifica la variabilidad de gran escala, habría que actualizar la variabilidad de pequeña escala). Este procedimiento se podría repetir iterativamente hasta convergencia (sería equivalente al método de estimación paramétrica tradicional propuesto por Neuman y Jacobson, 1984).
Modelado automático
La función np.fitgeo() implementa un procedimiento automático para la estimación conjunta de la tendencia y el semivariograma.
El algoritmo es el siguiente:
Seleccionar una ventana inicial para la estimación de la tendencia empleando el criterio MCV (función
h.cv()).Calcular la estimación lineal local de la tendencia (función
locpol()).Obtener una estimación piloto del semivariograma con corrección de sesgo
a partir de los residuos correspondientes (funciónnp.svariso.corr()).Ajustar un modelo válido de Shapiro-Botha a las estimaciones piloto del
semivariograma (funciónfitsvar.sb.iso()).Seleccionar una nueva matriz de ventanas para la estimación de la tendencia
con el criterio CGCV, utilizando el modelo ajustado de variograma
para aproximar la matriz de covarianzas de los datos (funciónh.cv()
conobjective = "GCV"ycov.bin =modelo de variograma ajustado).Repetir los pasos 2-5 hasta convergencia (por ejemplo, cuando no hay
cambios significativos en la estimación del variograma, ya que el criterio de selección de la ventana proporcionaría un suavizado similar). En la práctica, normalmente dos iteraciones6 suelen ser suficientes (el valor por defecto,iter = 2).
geomod <- np.fitgeo(x, y, nbin = c(30, 30), maxlag = 20,
svm.resid = TRUE, window = border)
plot(geomod)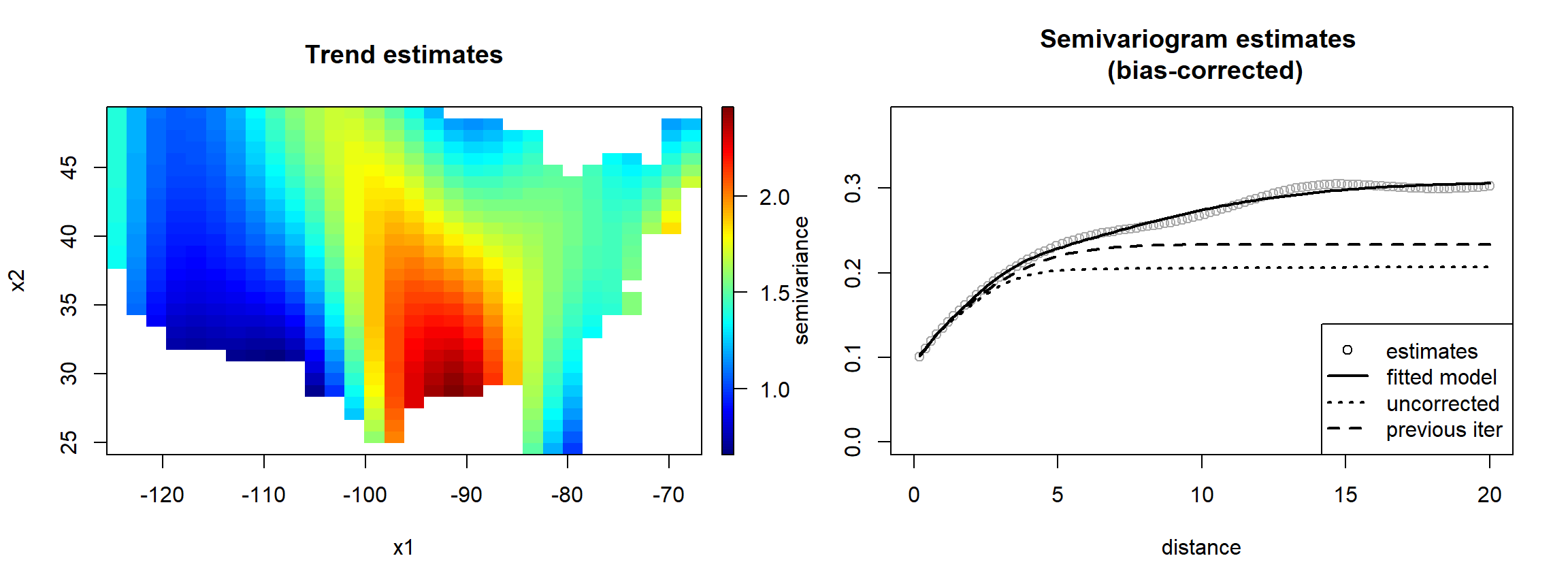
Establecer corr.svar = TRUE puede ser muy lento (y requerir mucha memoria) cuando el número de datos es muy grande (hay que tener en cuenta también que el sesgo del variograma residual disminuye a medida que aumenta el tamaño de la muestra).
Predicción kriging
La función genérica np.kriging() permite obtener predicciones mediante kriging residual (combinando la estimación de la tendencia con el kriging simple de los residuos).
krig.grid <- np.kriging(geomod, ngrid = c(120, 120))
# Plot kriging predictions and kriging standard deviations
old.par <- par(mfrow = c(1,2), omd = c(0.0, 0.98, 0.0, 1))
krig.grid2 <- krig.grid
simage(krig.grid2, 'kpred', main = 'Kriging predictions', slim = slim,
xlab = "Longitude", ylab = "Latitude" , col = col, asp = 1)
plot(border, border = "darkgray", lwd = 2, add = TRUE)
plot(interior, border = "lightgray", lwd = 1, add = TRUE)
simage(krig.grid2, 'ksd', main = 'Kriging sd',
xlab = "Longitude", ylab = "Latitude" , col = hot.colors(256), asp = 1)
plot(border, border = "darkgray", lwd = 2, add = TRUE)
plot(interior, border = "lightgray", lwd = 1, add = TRUE)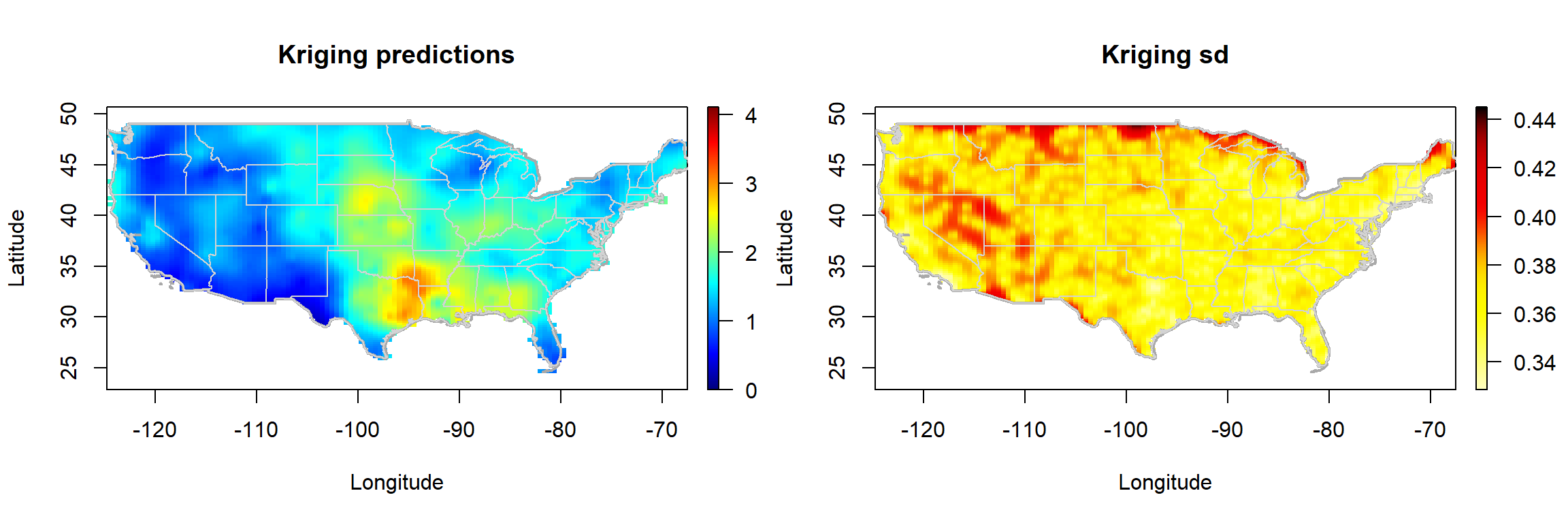
par(old.par)Actualmente solo está implementado kriging simple y kriging residual con vecindario global (para el cálculo de las predicciones se usa la factorización de Cholesky de la matriz de covarianzas, implementada en el paquete spam para matrices dispersas).
Alternativamente se puede emplear gstat::krige() (o gstat::krige.cv()) junto con la función as.vgm() para kriging local (ver por ejemplo la vignette Kriging with gstat).
Hay que tener en cuenta que las predicciones kriging son robustas y no dependen demasiado del modelo de tendencia (la variabilidad no explicada por la tendencia es capturada por la variabilidad de pequeña escala). Lo importante es la estimación del variograma cerca del origen.
Sin embargo, si se emplean las varianzas kriging (por ejemplo para el cálculo de intervalos de predicción) o otros métodos de inferencia (como contrastes de hipótesis o bootstrap) puede haber grandes diferencias entre los resultados obtenidos con distintos modelos.
Futuras implementaciones y temas abiertos
Bootstrap (condicional e incondicional):
Francisco-Fernandez M., Quintela-del-Rio A. and Fernandez-Casal R. (2012). Nonparametric methods for spatial regression. An application to seismic events, Environmetrics, 23, 85-93.
Fernández-Casal R., Castillo-Páez S. and Francisco-Fernández M. (2018). Nonparametric geostatistical risk mapping, Stochastic Environmental Research and Risk Assessment, 32, 675–684.
Castillo-Páez S., Fernández-Casal R. and García-Soidán P. (2019). A nonparametric bootstrap method for spatial data, Computational Statistics and Data Analysis, 137, 1-15.
Modelos anisotrópicos de semivariograma (caso espacio-temporal):
Fernández-Casal, R. (2003). Geoestadística espacio-temporal: modelos flexibles de variogramas anisotrópicos no separables. Tesis doctoral (USC). Director: Wenceslao González-Manteiga.
Fernandez-Casal R., Gonzalez-Manteiga W. and Febrero-Bande M. (2003). Flexible Spatio-Temporal Stationary Variogram Models, Statistics and Computing, 13, 127-136.
Procesos espaciales heterocedásticos:
Fernández-Casal R., Castillo-Páez S. and García-Soidán P. (2017). Nonparametric estimation of the small-scale variability of heteroscedastic spatial processes, Spatial Statistics, 22, 358-370.
Castillo-Páez S., Fernández-Casal R. and García-Soidán P. (2020). Nonparametric bootstrap approach for unconditional risk mapping under heteroscedasticity, Spatial Statistics, 40, 100389.
Otros temas abiertos (entre muchos otros):
Modelos aditivos y parcialmente lineales.
Kriging local.
Métodos geoestadísticos no paramétricos para datos masivos.
Estimación no paramétrica del variograma mediante FFT en datos reticulares (raster).
Estimación del variograma mediante FFT de datos discretizados (binning).
Predicción kriging empleando binning.
Modelos dinámicos (inclusión de variables explicativas cuyo efecto varía con el espacio o el tiempo).
Agradecimientos
Este trabajo ha sido financiado por el MINECO a través del proyecto MTM2017-82724-R, y por la Xunta de Galicia (Grupos de Referencia Competitiva ED431C-2020-14 y Centro Investigación del Sistema universitario de Galicia ED431G 2019/01). Todas estas ayudas fueron cofinanciadas por el FEDER.
Referencias
Castillo-Páez, S. (2017). Aportaciones a la Geoestadística no paramétrica. Tesis doctoral (UVigo). Directores: Pilar García-Soidán, Rubén Fernández-Casal.
Chu, C.K. and Marron, J.S. (1991). Comparison of Two Bandwidth Selectors with Dependent Errors. The Annals of Statistics, 19, 1906-1918.
Cressie, N. (1993). Statistics for Spatial Data. Wiley, New York.
Fan, J. and Gijbels, I. (1996). Local polynomial modelling and its applications. Chapman & Hall, London.
Fernandez-Casal R. (2021).
npsp: Nonparametric Spatial Statistics. R package version 0.7.8.Fernández-Casal R. y Costa J. (2021). Aprendizaje Estadístico. https://rubenfcasal.github.io/aprendizaje_estadistico.
Fernandez-Casal R. and Francisco-Fernandez M. (2014) Nonparametric bias-corrected variogram estimation under non-constant trend, Stochastic Environmental Research and Risk Assessment, 28, 1247-1259.
Fernandez-Casal R., Gonzalez-Manteiga W. and Febrero-Bande M. (2003). Space‐time dependency modeling using general classes of flexible stationary variogram models, Journal of Geophysical Research-Atmospheres, 108, 8779, D24.
Francisco-Fernandez M. and Opsomer J.D. (2005) Smoothing parameter selection methods for nonparametric regression with spatially correlated errors, Canadian Journal of Statistics, 33, 539-558.
García-Portugués E. (2021). Notes for Nonparametric Statistics. https://bookdown.org/egarpor/NP-UC3M/.
Opsomer, J. D., Wang, Y. and Yang, Y. (2001). Nonparametric regression with correlated errors. Statistical Science 16, 134–153.
Rupert D. and Wand M.P. (1994). Multivariate locally weighted least squares regression. The Annals of Statistics, 22, 1346-1370.
Shapiro A. and Botha J.D. (1991). Variogram fitting with a general class of conditionally non-negative definite functions. Computational Statistics and Data Analysis, 11, 87-96.
Wand M.P. (1994). Fast Computation of Multivariate Kernel Estimators. Journal of Computational and Graphical Statistics, 3, 433-445.
Wand M.P. and Jones M.C. (1995). Kernel Smoothing. Chapman and Hall, London.
Ver también referencias en la Sección Futuras implementaciones.
El objetivo en el futuro es considerar procesos puntuales marcados: \(D\) es un proceso puntual en \(\mathbb{R}^{d}\).↩︎
Por ejemplo esto se hace para la obtención de los residuos.↩︎
Como se trata de una minimización no lineal multidimensional puede haber problemas de mínimos locales. Para intentar evitar este problema se puede establecer unos valores iniciales para los parámetros de la ventana mediante el argumento
h.start. Alternativamente se puede establecer el parámetroDEalgorithm = TRUEpara utilizar el algoritmo genético de optimización del paqueteDEoptim(aunque puede aumentar considerablemente el tiempo de computación).↩︎Este criterio no tiene en cuenta la dependencia entre las semivarianzas, por lo que las ventanas seleccionadas tenderán a infrasuavizar (especialmente en saltos grandes). Si se emplea un procedimiento automático, puede ser recomendable incrementar la ventana obtenida con estos criterios (en el algoritmo automático implementado en
np.fitgeo()descrito en la siguiente sección, si no se especifica la ventana para la estimación del variograma, se incrementa por defecto la ventana obtenida conh.cv()en un 50%).↩︎Estos modelos son muy flexibles, por lo que es habitual considerar modelos válidos en dimensiones mayores que la de los datos para obtener ajustes más suaves (empleando el parámetro
dk). En el límite obtendríamos un modelo válido en cualquier dimensión (se selecciona estableciendodk = 0).↩︎El parámetro
itercontrola el número máximo de iteraciones del algoritmo completo. Estableciendoiter = 0se emplea el variograma residual.↩︎