7.1 Regresión local
Los métodos de regresión local incluyen: vecinos más próximos, regresión tipo núcleo y loess (o lowess). También se podrían incluir los splines de regresión (regression splines), pero los trataremos en la siguiente sección, ya que también se pueden ver como una extensión de un modelo lineal global.
Con la mayoría de estos procedimientos no se obtiene una expresión cerrada del modelo ajustado y, en principio, es necesario disponer de la muestra de entrenamiento para poder realizar las predicciones. Por esta razón, en aprendizaje estadístico también se les denomina métodos basados en memoria.
7.1.1 Vecinos más próximos
Uno de los métodos más conocidos de regresión local es el denominado k-vecinos más cercanos (k-nearest neighbors; KNN), que ya se empleó como ejemplo en la Sección 1.4, dedicada a la maldición de la dimensionalidad. Aunque se trata de un método muy simple, en la práctica puede resultar efectivo en numerosas ocasiones. Se basa en la idea de que, localmente, la media condicional (la predicción óptima) es constante. Concretamente, dados un entero \(k\) (hiperparámetro) y un conjunto de entrenamiento \(\mathcal{T}\), para obtener la predicción correspondiente a un vector de valores de las variables explicativas \(\mathbf{x}\), el método de regresión KNN promedia las observaciones en un vecindario \(\mathcal{N}_k(\mathbf{x}, \mathcal{T})\) formado por las \(k\) observaciones más cercanas a \(\mathbf{x}\): \[\hat{Y}(\mathbf{x}) = \hat{m}(\mathbf{x}) = \frac{1}{k} \sum_{i \in \mathcal{N}_k(\mathbf{x}, \mathcal{T})} Y_i\] Se puede emplear la misma idea en el caso de clasificación: las frecuencias relativas en el vecindario serían las estimaciones de las probabilidades de las clases (lo que sería equivalente a considerar las variables indicadoras de las categorías) y, por lo general, la predicción se haría utilizando la moda (es decir, la clase más probable).
Para seleccionar el vecindario es necesario especificar una distancia, por ejemplo: \[d(\mathbf{x}_0, \mathbf{x}_i) = \left( \sum_{j=1}^p \left| x_{j0} - x_{ji} \right|^d \right)^{\frac{1}{d}}\] Normalmente, si los predictores son muméricos se considera la distancia euclídea (\(d=2\)) o la de Manhattan (\(d=1\)) (también existen distancias diseñadas para predictores categóricos). En todos los casos se recomienda estandarizar previamente los predictores para que su escala no influya en el cálculo de las distancias.
Como ya se indicó previamente, este método está implementado en la función knnreg() (Sección 1.4) y en el método "knn" del paquete caret (Sección 1.6).
Como ejemplo adicional, emplearemos el conjunto de datos MASS::mcycle, que contiene mediciones de la aceleración de la cabeza en una simulación de un accidente de motocicleta, utilizado para probar cascos protectores. Consideraremos el conjunto de datos completo como si fuese la muestra de entrenamiento (ver Figura 7.1):
data(mcycle, package = "MASS")
library(caret)
# Ajuste de los modelos
fit1 <- knnreg(accel ~ times, data = mcycle, k = 5) # 5% de los datos
fit2 <- knnreg(accel ~ times, data = mcycle, k = 10)
fit3 <- knnreg(accel ~ times, data = mcycle, k = 20)
# Representación
plot(accel ~ times, data = mcycle, col = 'darkgray')
newx <- seq(1 , 60, len = 200)
newdata <- data.frame(times = newx)
lines(newx, predict(fit1, newdata), lty = 3)
lines(newx, predict(fit2, newdata), lty = 2)
lines(newx, predict(fit3, newdata))
legend("topright", legend = c("5-NN", "10-NN", "20-NN"),
lty = c(3, 2, 1), lwd = 1)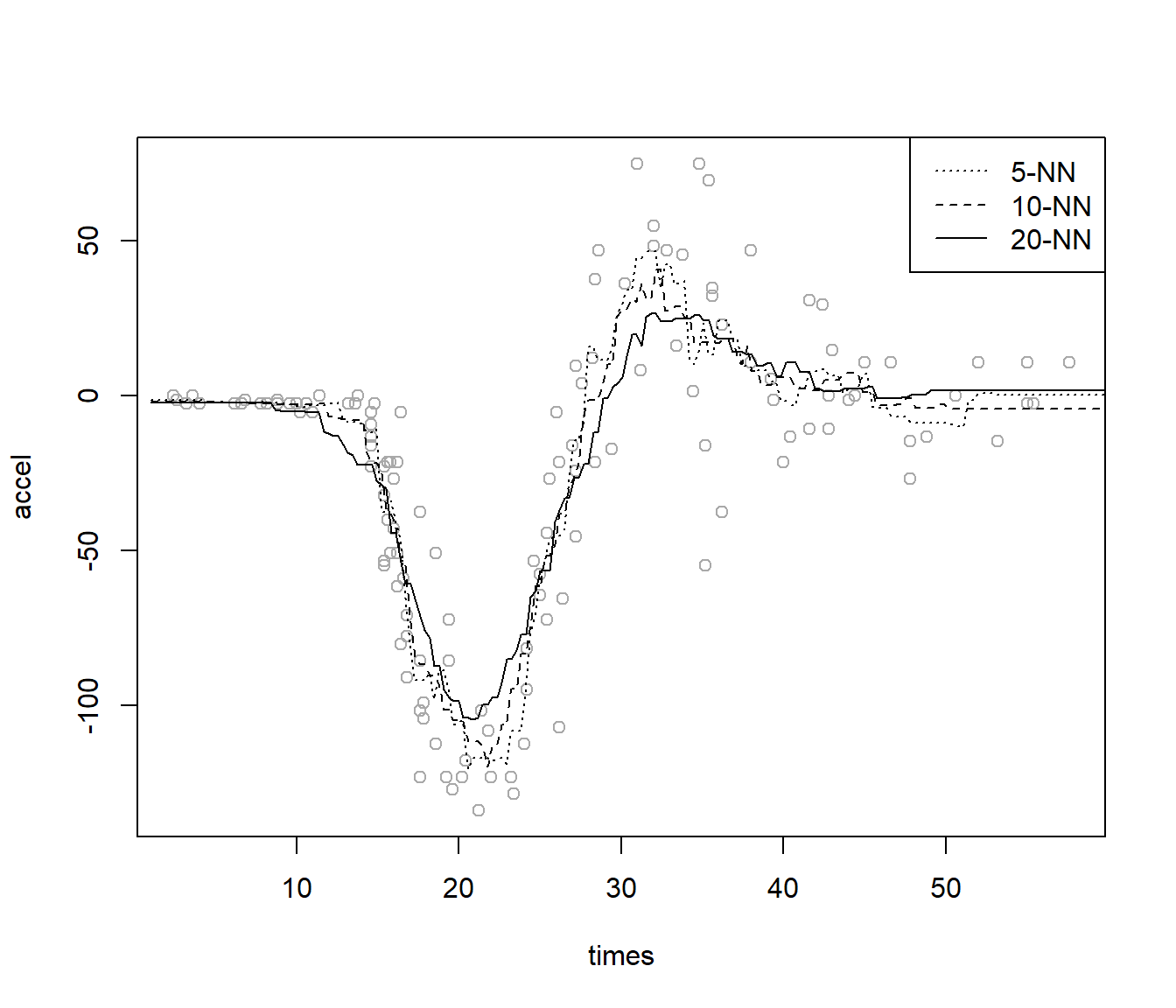
Figura 7.1: Predicciones con el método KNN y distintos vecindarios.
El hiperparámetro \(k\) (número de vecinos más próximos) determina la complejidad del modelo, de forma que valores más pequeños de \(k\) se corresponden con modelos más complejos (en el caso extremo \(k = 1\) se interpolarían las observaciones). Este parámetro se puede seleccionar empleando alguno de los métodos descritos en la Sección 1.3.3 (por ejemplo, mediante validación cruzada, como se mostró en la Sección 1.6; ver Ejercicio 7.1).
El método de los vecinos más próximos también se puede utilizar, de forma análoga, para problemas de clasificación. En este caso obtendríamos estimaciones de las probabilidades de cada categoría: \[\hat{p}_j(\mathbf{x}) = \frac{1}{k} \sum_{i \in \mathcal{N}_k(\mathbf{x}, \mathcal{T})} \mathcal I (y_i = j)\] A partir de las cuales obtenemos la predicción de la respuesta categórica, como la categoría con mayor probabilidad estimada (ver Ejercicio 7.2).
Ejercicio 7.1 Repite el ajuste anterior, usando knnreg(), seleccionando el número de k vecinos mediante validación cruzada dejando uno fuera y empleando el mínimo error absoluto medio como criterio.
Se puede utilizar como referencia el código de la Sección 1.3.3.
Ejercicio 7.2 En la Sección 1.3.5 se utilizó el conjunto de datos iris como ejemplo de un problema de clasificación multiclase, con el objetivo de clasificar tres especies de lirio (Species) a partir de las dimensiones de los sépalos y pétalos de sus flores.
Retomando ese ejemplo, realiza esta clasificación empleando el método knn de caret.
Considerando el 80 % de las observaciones como muestra de aprendizaje y el 20 % restante como muestra de test, selecciona el número de vecinos mediante validación cruzada con 10 grupos, empleando el criterio de un error estándar de Breiman.
Finalmente, evalúa la eficiencia de las predicciones en la muestra de test.
7.1.2 Regresión polinómica local
La regresión polinómica local univariante consiste en ajustar, por mínimos cuadrados ponderados, un polinomio de grado \(d\) para cada \(x_0\): \[\beta_0+\beta_{1}\left(x - x_0\right) + \cdots + \beta_{d}\left( x-x_0\right)^{d}\] con pesos \[w_{i} = K_h(x - x_0) = \frac{1}{h}K\left(\frac{x-x_0}{h}\right)\] donde \(K\) es una función núcleo (habitualmente una función de densidad simétrica en torno a cero) y \(h>0\) es un parámetro de suavizado, llamado ventana, que regula el tamaño del entorno que se usa para llevar a cabo el ajuste. En la expresión anterior se está considerando una ventana global, la misma para todos puntos, pero también se puede emplear una ventana local, \(h \equiv h(x_0)\). Por ejemplo, el método KNN se puede considerar un caso particular, con ventana local, \(d=0\) (se ajusta una constante) y núcleo \(K\) uniforme, la función de densidad de una distribución \(\mathcal{U}(-1, 1)\). Como resultado de los ajustes locales obtenemos la estimación en \(x_0\): \[\hat{m}_{h}(x_0)=\hat{\beta}_0\] y también podríamos obtener estimaciones de las derivadas \(\widehat{m_{h}^{(r)}}(x_0) = r!\hat{\beta}_{r}\).
Por tanto, la estimación polinómica local de grado \(d\), \(\hat{m}_{h}(x)=\hat{\beta}_0\), se obtiene al minimizar: \[\min_{\beta_0 ,\beta_1, \ldots, \beta_d} \sum_{i=1}^{n}\left\{ Y_{i} - \beta_0 - \beta_1(x - X_i) - \ldots -\beta_d(x - X_i)^d \right\}^{2} K_{h}(x - X_i)\]
Explícitamente: \[\hat{m}_{h}(x) = \mathbf{e}_{1}^{t} \left( X_{x}^{t} {W}_{x} X_{x} \right)^{-1} X_{x}^{t} {W}_{x}\mathbf{Y} \equiv {s}_{x}^{t}\mathbf{Y}\] donde \(\mathbf{e}_{1} = \left( 1, \cdots, 0\right)^{t}\), \(X_{x}\) es la matriz con \((1,x - X_i, \ldots, (x - X_i)^d)\) en la fila \(i\), \(W_{x} = \mathtt{diag} \left( K_{h}(x_{1} - x), \ldots, K_{h}(x_{n} - x) \right)\) es la matriz de pesos, e \(\mathbf{Y} = \left( Y_1, \cdots, Y_n\right)^{t}\) es el vector de observaciones de la respuesta.
Se puede pensar que la estimación anterior se obtiene aplicando un suavizado polinómico a \((X_i, Y_i)\): \[\hat{\mathbf{Y}} = S\mathbf{Y}\] siendo \(S\) la matriz de suavizado con \(\mathbf{s}_{X_{i}}^{t}\) en la fila \(i\) (este tipo de métodos también se denominan suavizadores lineales).
En lo que respecta a la selección del grado \(d\) del polinomio, lo más habitual es utilizar el estimador de Nadaraya-Watson (\(d=0\)) o el estimador lineal local (\(d=1\)). Desde el punto de vista asintótico, ambos estimadores tienen un comportamiento similar61, pero en la práctica suele ser preferible el estimador lineal local, sobre todo porque se ve menos afectado por el denominado efecto frontera (Sección 1.4).
La ventana \(h\) es el hiperparámetro de mayor importancia en la predicción y para su selección se suelen emplear métodos de validación cruzada (Sección 1.3.3) o tipo plug-in (Ruppert et al., 1995).
En este último caso, se reemplazan las funciones desconocidas que aparecen en la expresión de la ventana asintóticamente óptima por estimaciones (p. ej. función dpill() del paquete KernSmooth).
Así, usando el criterio de validación cruzada dejando uno fuera (LOOCV), se trataría de minimizar:
\[CV(h)=\frac{1}{n}\sum_{i=1}^n(y_i-\hat{m}_{-i}(x_i))^2\]
siendo \(\hat{m}_{-i}(x_i)\) la predicción obtenida eliminando la observación \(i\)-ésima.
Al igual que en el caso de regresión lineal, este error también se puede obtener a partir del ajuste con todos los datos:
\[CV(h)=\frac{1}{n}\sum_{i=1}^n\left(\frac{y_i-\hat{m}(x_i)}{1 - S_{ii}}\right)^2\]
siendo \(S_{ii}\) el elemento \(i\)-ésimo de la diagonal de la matriz de suavizado (esto en general es cierto para cualquier suavizador lineal).
Alternativamente, se podría emplear validación cruzada generalizada (Craven y Wahba, 1978), sin más que sustituir \(S_{ii}\) por su promedio: \[GCV(h)=\frac{1}{n}\sum_{i=1}^n\left(\frac{y_i-\hat{m}(x_i)}{1 - \frac{1}{n}tr(S)}\right)^2\] La traza de la matriz de suavizado, \(tr(S)\), se conoce como el número efectivo de parámetros y, para aproximar los grados de libertad del error, se utiliza (\(n - tr(S)\).
Aunque el paquete base de R incluye herramientas para la estimación tipo núcleo de la regresión (ksmooth(), loess()), se recomienda el uso del paquete KernSmooth (Wand, 2023).
Continuando con el ejemplo del conjunto de datos MASS::mcycle, emplearemos la función locpoly() del paquete KernSmooth para obtener estimaciones lineales locales62 con una ventana seleccionada mediante un método plug-in (ver Figura 7.2):
# data(mcycle, package = "MASS")
times <- mcycle$times
accel <- mcycle$accel
library(KernSmooth)
h <- dpill(times, accel) # Método plug-in
fit <- locpoly(times, accel, bandwidth = h) # Estimación lineal local
plot(times, accel, col = 'darkgray')
lines(fit)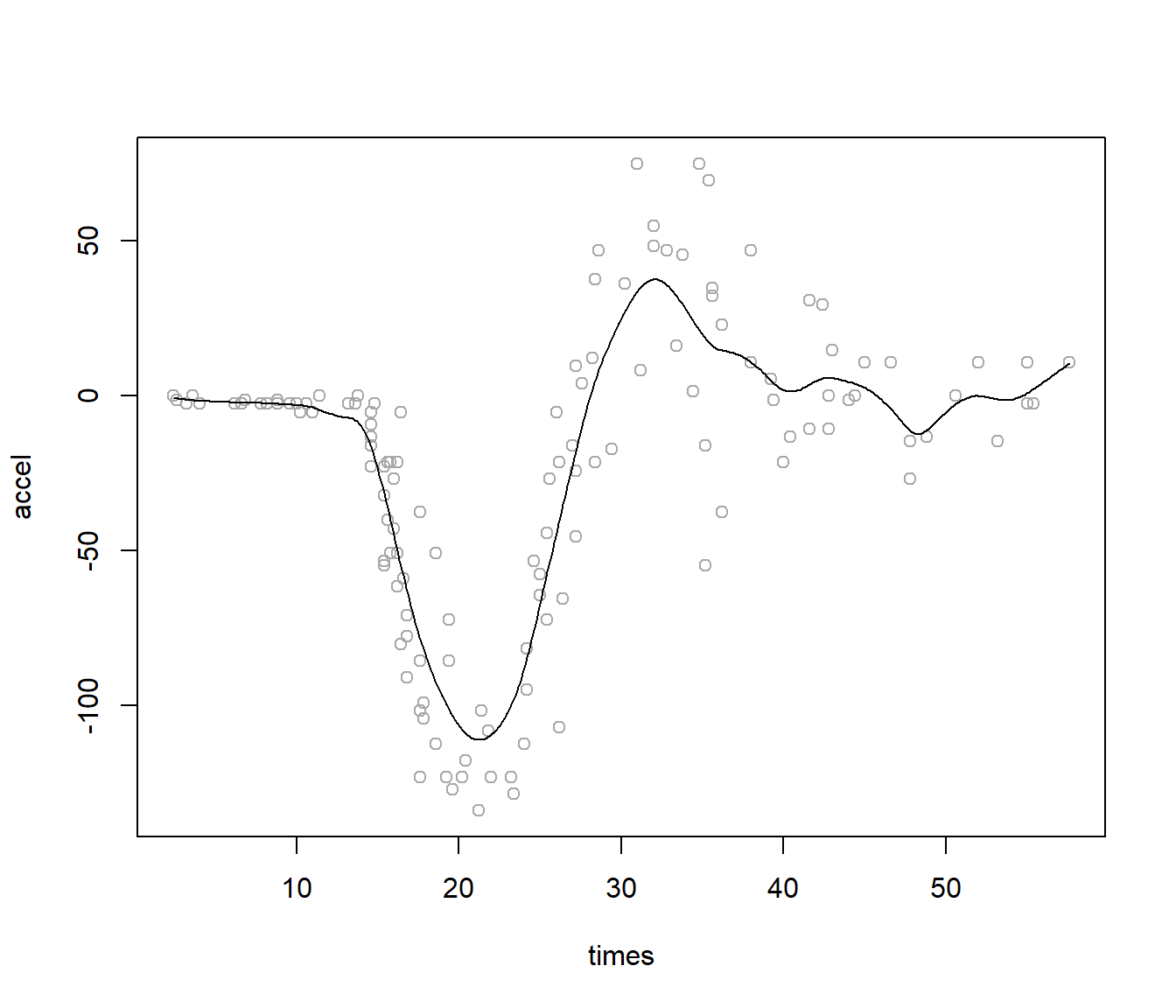
Figura 7.2: Ajuste lineal local con ventana plug-in.
Hay que tener en cuenta que el paquete KernSmooth no implementa los métodos predict() y residuals().
El resultado del ajuste es una rejilla con las predicciones y podríamos emplear interpolación para calcular predicciones en otras posiciones:
pred <- approx(fit, xout = times)$y
resid <- accel - pred Tampoco calcula medidas de bondad de ajuste, aunque podríamos calcular medidas de la precisión de las predicciones de la forma habitual (en este caso de la muestra de entrenamiento):
accuracy(pred, accel)## me rmse mae mpe mape r.squared
## -2.7124e-01 2.1400e+01 1.5659e+01 -2.4608e+10 7.5592e+10 8.0239e-01La regresión polinómica local multivariante es análoga a la univariante, aunque en este caso habría que considerar una matriz de ventanas simétrica \(H\). También hay extensiones para el caso de predictores categóricos (nominales o ordinales) y para el caso de distribuciones de la respuesta distintas de la normal (máxima verosimilitud local).
Otros paquetes de R incluyen más funcionalidades (sm, locfit, npsp…), pero hoy en día el paquete np (Racine y Hayfield, 2023) es el que se podría considerar más completo.
7.1.3 Regresión polinómica local robusta
Se han desarrollado variantes robustas del ajuste polinómico local tipo núcleo.
Estos métodos surgieron en el caso bivariante (\(p=1\)), por lo que también se denominan suavizado de diagramas de dispersión (scatterplot smoothing; p. ej. la función lowess() del paquete base de R, acrónimo de locally weighted scatterplot smoothing).
Posteriormente se extendieron al caso multivariante (p. ej. la función loess()).
Son métodos muy empleados en análisis descriptivo (no supervisado) y normalmente se emplean ventanas locales tipo vecinos más cercanos (por ejemplo a través de un parámetro span que determina la proporción de observaciones empleadas en el ajuste).
Como ejemplo continuaremos con el conjunto de datos MASS::mcycle y emplearemos la función loess() para realizar un ajuste robusto.
Será necesario establecer family = "symmetric" para emplear M-estimadores, por defecto con 4 iteraciones, en lugar de mínimos cuadrados ponderados.
Previamente, seleccionaremos el parámetro span por validación cruzada (LOOCV), pero empleando como criterio de error la mediana de los errores en valor absoluto (median absolute deviation, MAD)63 (ver Figura 7.3).
# Función que calcula las predicciones LOOCV
cv.loess <- function(formula, datos, span, ...) {
n <- nrow(datos)
cv.pred <- numeric(n)
for (i in 1:n) {
modelo <- loess(formula, datos[-i, ], span = span,
control = loess.control(surface = "direct"), ...)
# loess.control(surface = "direct") permite extrapolaciones
cv.pred[i] <- predict(modelo, newdata = datos[i, ])
}
return(cv.pred)
}
# Búsqueda valor óptimo
ventanas <- seq(0.1, 0.5, len = 10)
np <- length(ventanas)
cv.error <- numeric(np)
for(p in 1:np){
cv.pred <- cv.loess(accel ~ times, mcycle, ventanas[p],
family = "symmetric")
# cv.error[p] <- mean((cv.pred - mcycle$accel)^2)
cv.error[p] <- median(abs(cv.pred - mcycle$accel))
}
imin <- which.min(cv.error)
span.cv <- ventanas[imin]
# Representación
plot(ventanas, cv.error)
points(span.cv, cv.error[imin], pch = 16)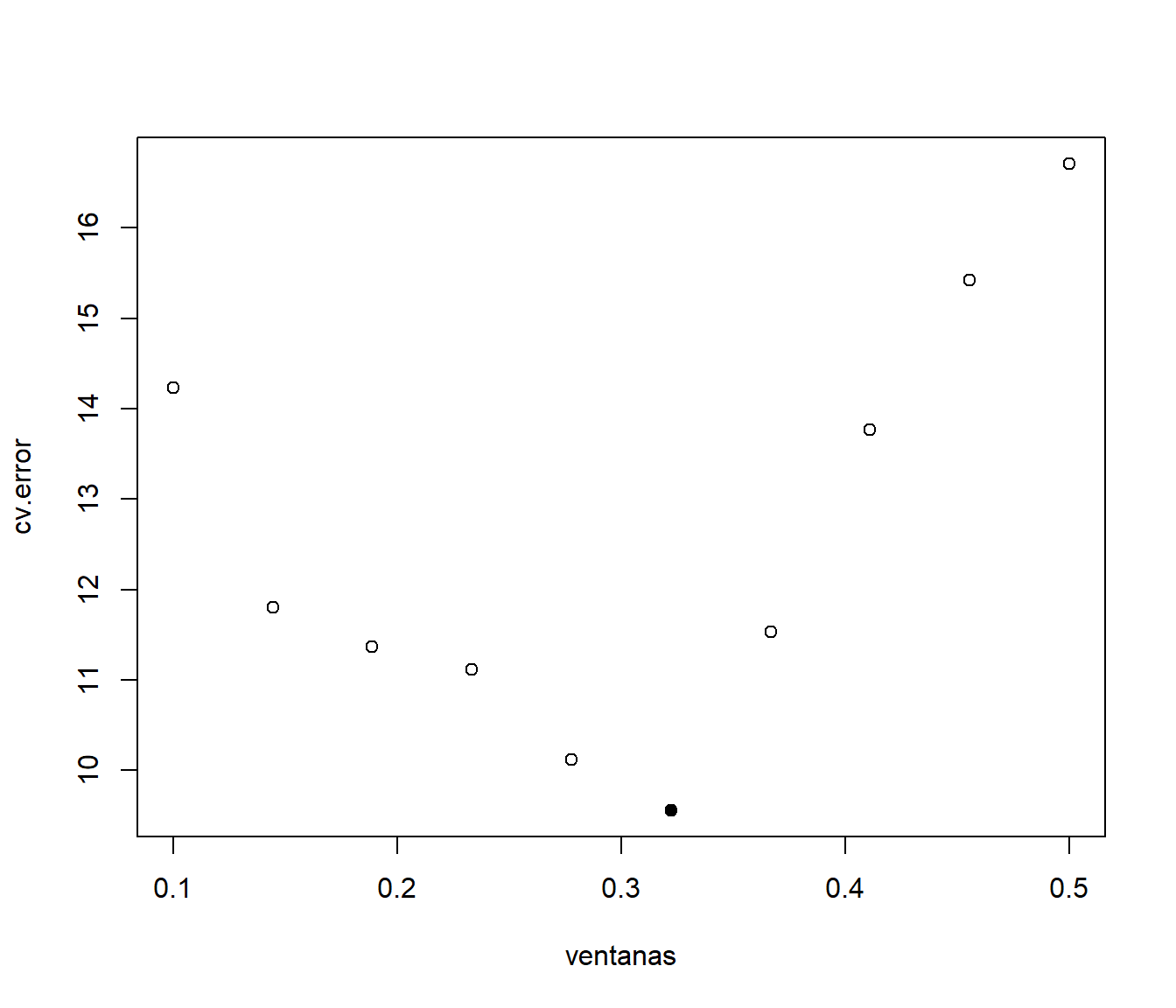
Figura 7.3: Error de predicción de validación cruzada (mediana de los errores absolutos) del ajuste LOWESS dependiendo del parámetro de suavizado.
Empleamos el parámetro de suavizado seleccionado para ajustar el modelo final (ver Figura 7.4):
# Ajuste con todos los datos
plot(accel ~ times, data = mcycle, col = 'darkgray')
fit <- loess(accel ~ times, mcycle, span = span.cv, family = "symmetric")
lines(mcycle$times, predict(fit))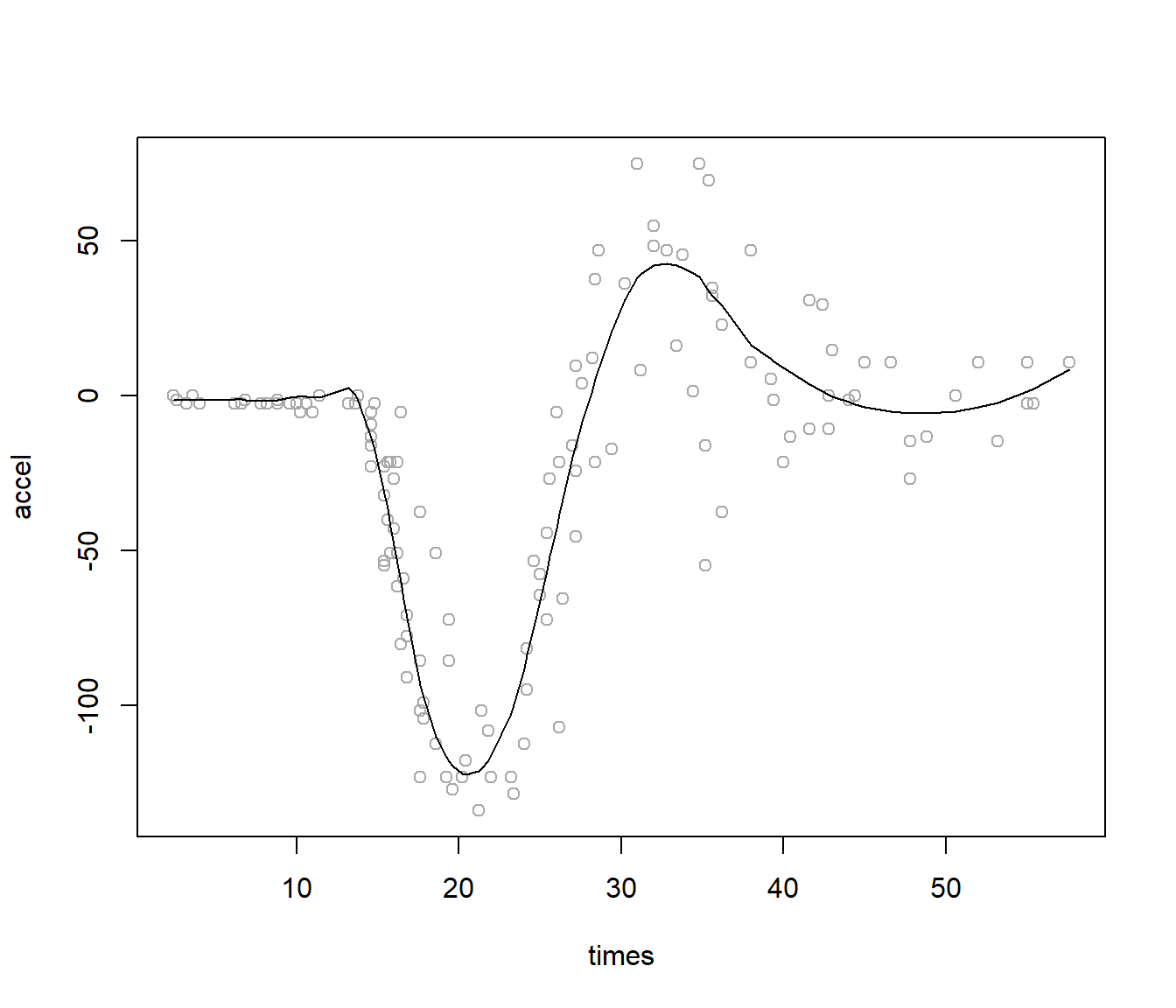
Figura 7.4: Ajuste polinómico local robusto (LOWESS), con el parámetro de suavizado seleccionado mediante validación cruzada.
Bibliografía
Asintóticamente el estimador lineal local tiene un sesgo menor que el de Nadaraya-Watson (pero del mismo orden) y la misma varianza (p. ej. Fan y Gijbels (1996)).↩︎
La función
KernSmooth::locpoly()también admite la estimación de derivadas.↩︎En este caso hay dependencia entre las observaciones y los criterios habituales, como validación cruzada, tienden a seleccionar ventanas pequeñas, i. e. a infrasuavizar.↩︎