6.4 Análisis de la varianza

6.4.1 ANOVA con un factor

Vamos a estudiar si hay diferencias en las medias de la variable satisfac (satisfacción global) entre los diferentes grupos definidos por nfidelid (nivel de compra), utilizando el procedimiento clásico de análisis de la varianza. Este procedimiento exige normalidad y homocedasticidad.

table(hatco$nfidelid)

## 
##  bajo medio  alto 
##     3    64    33

tapply(hatco$satisfac, hatco$nfidelid, mean, na.rm = TRUE)

##     bajo    medio     alto 
## 3.533333 4.498437 5.443750

La variable explicativa tiene que ser obligatoriamente de tipo factor. Por coherencia con la función (general) lm, la variación entre grupos está etiquetada nfidelid, y la variación dentro de los grupos como Residuals

anova(lm(satisfac~nfidelid, data = hatco))

## Analysis of Variance Table
## 
## Response: satisfac
##           Df Sum Sq Mean Sq F value    Pr(>F)    
## nfidelid   2 23.832 11.9158  23.588 4.647e-09 ***
## Residuals 96 48.495  0.5052                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Como alternativa, se puede utilizar la función aov

aov(satisfac~nfidelid, data = hatco)

## Call:
##    aov(formula = satisfac ~ nfidelid, data = hatco)
## 
## Terms:
##                 nfidelid Residuals
## Sum of Squares  23.83161  48.49526
## Deg. of Freedom        2        96
## 
## Residual standard error: 0.7107454
## Estimated effects may be unbalanced
## 1 observation deleted due to missingness

summary(aov(satisfac~nfidelid, data = hatco))

##             Df Sum Sq Mean Sq F value   Pr(>F)    
## nfidelid     2  23.83  11.916   23.59 4.65e-09 ***
## Residuals   96  48.50   0.505                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 1 observation deleted due to missingness

Comparaciones entre pares de variables

pairwise.t.test(hatco$satisfac, hatco$nfidelid)

## 
##  Pairwise comparisons using t tests with pooled SD 
## 
## data:  hatco$satisfac and hatco$nfidelid 
## 
##       bajo    medio  
## medio 0.024   -      
## alto  4.6e-05 5.5e-08
## 
## P value adjustment method: holm

Relajamos la hipótesis de varianzas iguales

oneway.test(satisfac~nfidelid, data = hatco)

## 
##  One-way analysis of means (not assuming equal variances)
## 
## data:  satisfac and nfidelid
## F = 35.013, num df = 2.0000, denom df = 6.7661, p-value = 0.0002697

Podemos utilizar el test de Bartlett para contrastar la igualdad de varianzas

bartlett.test(satisfac~nfidelid, data = hatco)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  satisfac by nfidelid
## Bartlett's K-squared = 1.4922, df = 2, p-value = 0.4742

Representación gráfica

medias <- tapply(hatco$satisfac, hatco$nfidelid, mean, na.rm = TRUE)
desviaciones <- tapply(hatco$satisfac, hatco$nfidelid, sd, na.rm = TRUE)
n <- tapply(hatco$satisfac[!is.na(hatco$satisfac)], hatco$nfidelid[!is.na(hatco$satisfac)], length)
errores <- desviaciones/sqrt(n)
stripchart(hatco$satisfac~hatco$nfidelid, method='jitter', jit=0.01, pch=18, col='grey', vertical = TRUE)
arrows(1:3, medias+errores, 1:3, medias-errores, angle=90, code=3, lwd=2, col='orange')
points(1:3, medias, pch=4, lwd=2, cex=2, col='orange')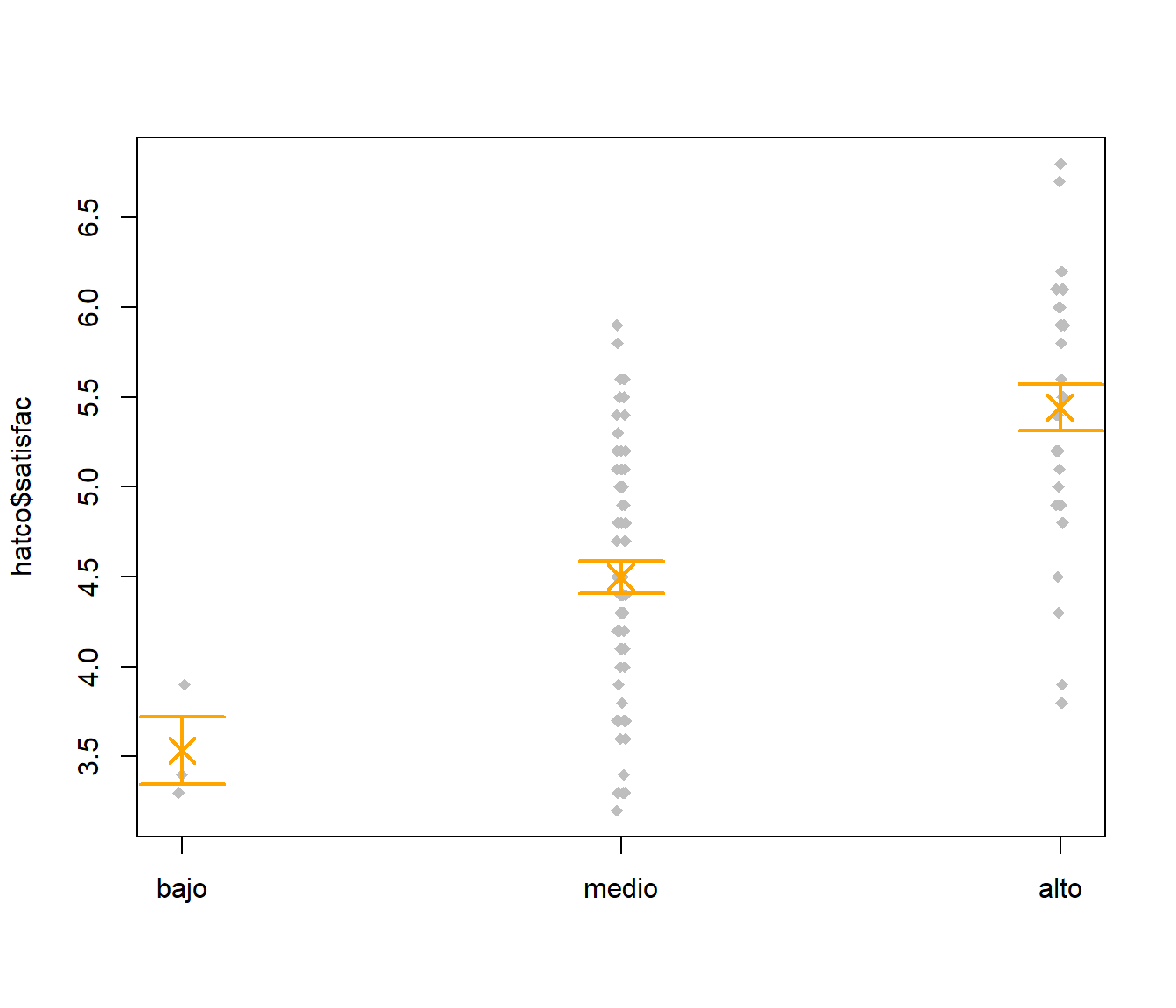

6.4.2 Test de Kruskal-Wallis

Alternativa no paramétrica al análisis de la varianza con un factor

kruskal.test(satisfac~nfidelid, data = hatco)

## 
##  Kruskal-Wallis rank sum test
## 
## data:  satisfac by nfidelid
## Kruskal-Wallis chi-squared = 31.073, df = 2, p-value = 1.789e-07