5.2 Gráficos

5.2.1 Diagrama de barras y gráfico de sectores

table(catlab)

## catlab
## Administrativo      Seguridad      Directivo 
##            363             27             84

par(mfrow = c(1, 3))
barplot(table(catlab),main="frecuencia absoluta")
barplot(100*prop.table(table(catlab)),main="frecuencia relativa (%)")
pie(table(catlab))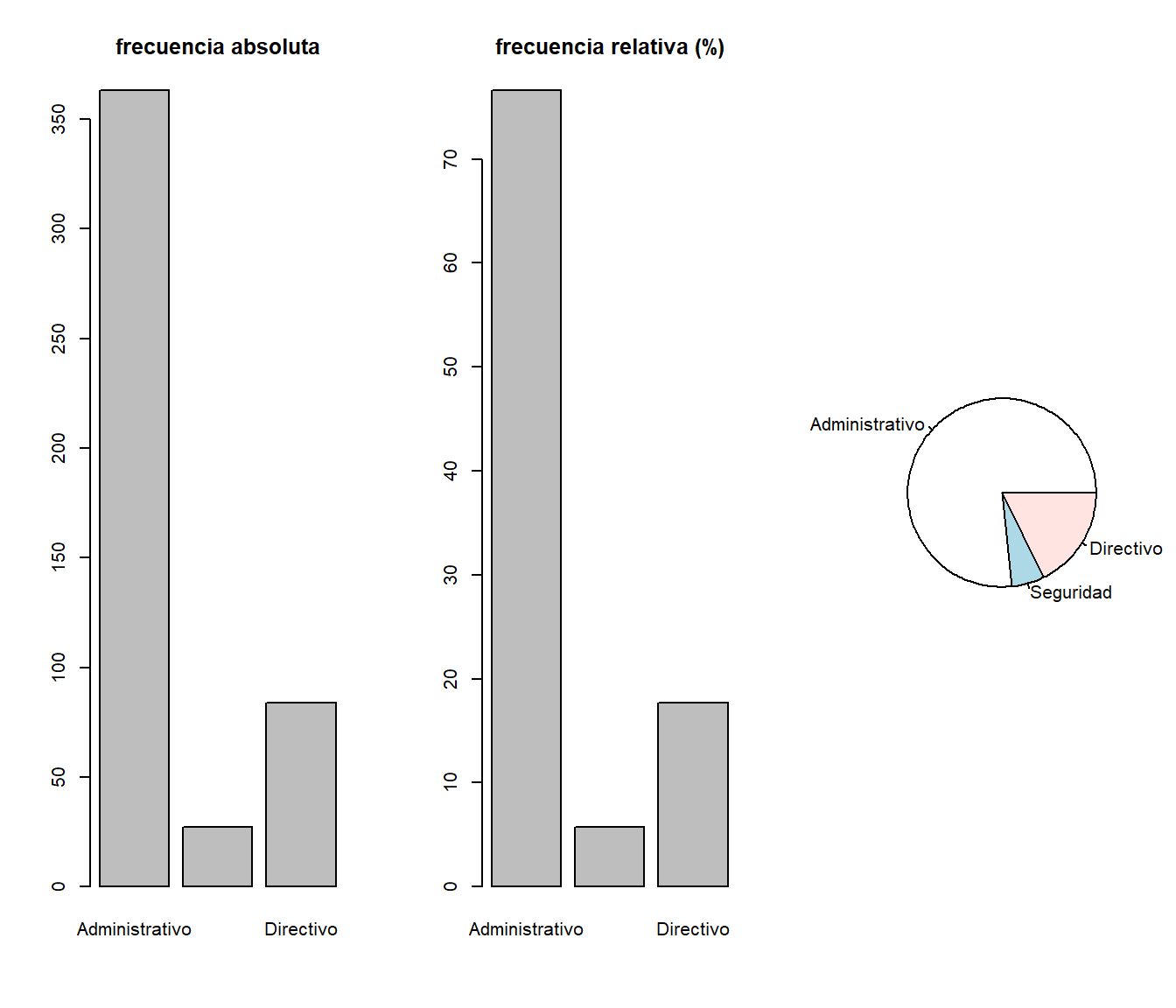

nj <- table(educ)
fj <- prop.table(nj)
Nj <- cumsum(nj)
Fj <- cumsum(fj)
layout(matrix(c(1,2,5,3,4,5), 2, 3, byrow=TRUE), respect=TRUE)
barplot(nj,main="frecuencia absolutas",xlab='años de estudio')
barplot(fj,main="frecuencia relativas",xlab='años de estudio')
barplot(Nj,main="frecuencia absolutas acumuladas",xlab='años de estudio')
barplot(Fj,main="frecuencia relativas acumuladas",xlab='años de estudio')
pie(nj,col=rainbow(6),main='años de estudio')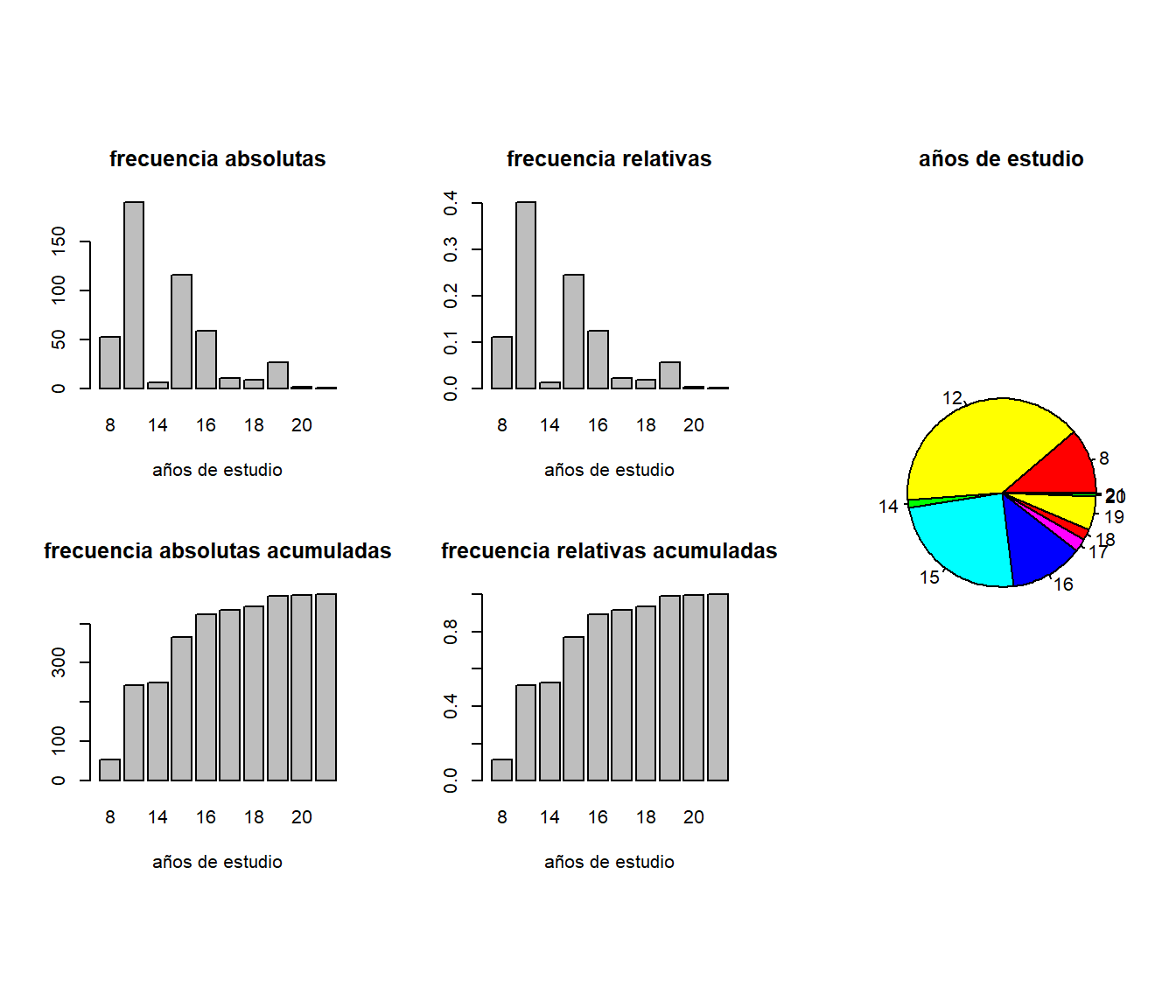

par(mfrow = c(1, 1))

Con datos continuos, podemos hacer uso de la función cut (más adelante veremos como se representa el histograma)

table(cut(expprev, breaks=5))

## 
## (-0.476,95.2]    (95.2,190]     (190,286]     (286,381]     (381,476] 
##           312            81            46            22            13

barplot(table(cut(expprev,breaks=5)),xlab="Experiencia previa",
        main="Categorización en 5 clases")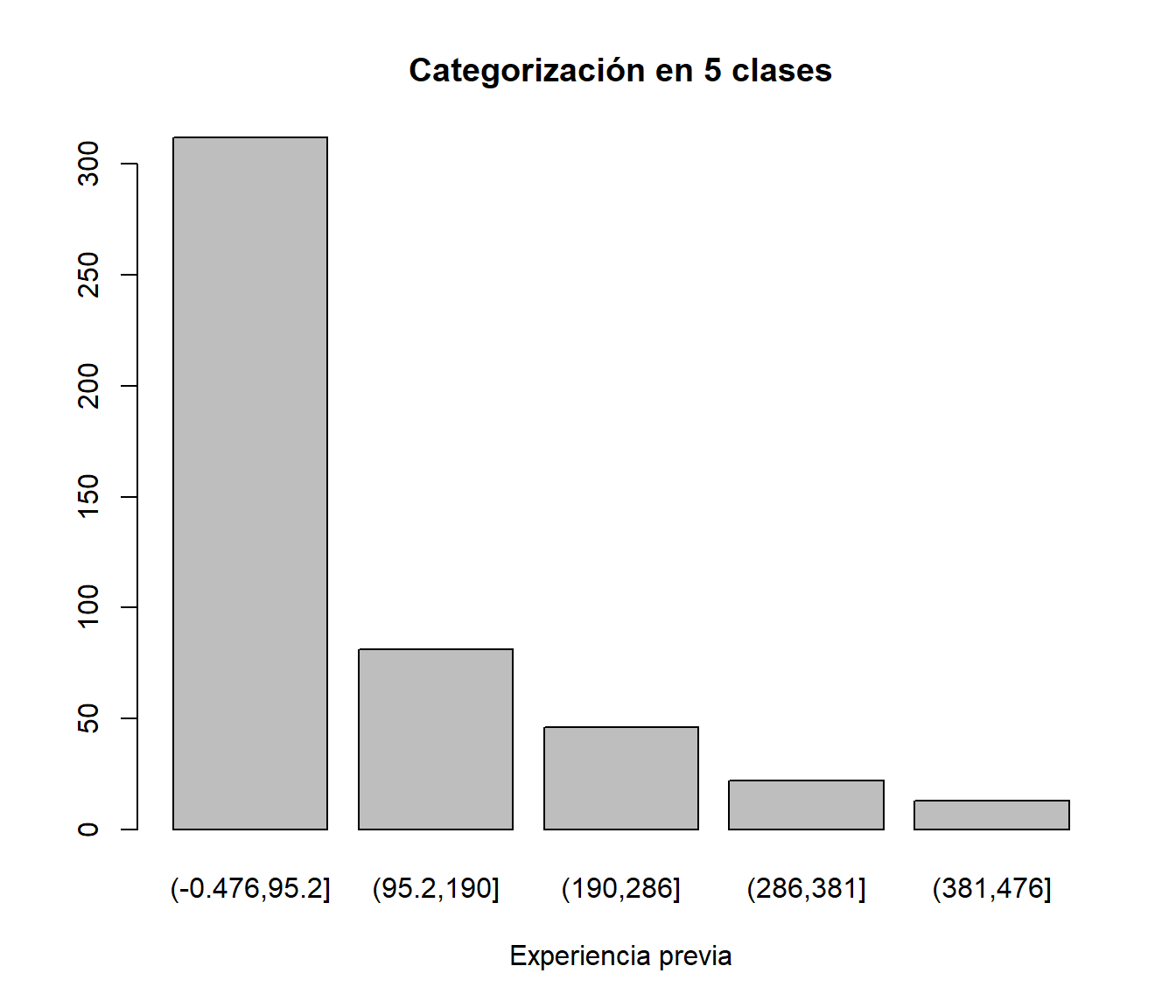

Debemos ser muy cuidadosos a la hora de valorar gráficas como la siguiente

tt <- table(cut(expprev, breaks=c(0,40,80,150,250,400)))
barplot(tt,xlab="Experiencia previa", main="Categorización en 5 clases")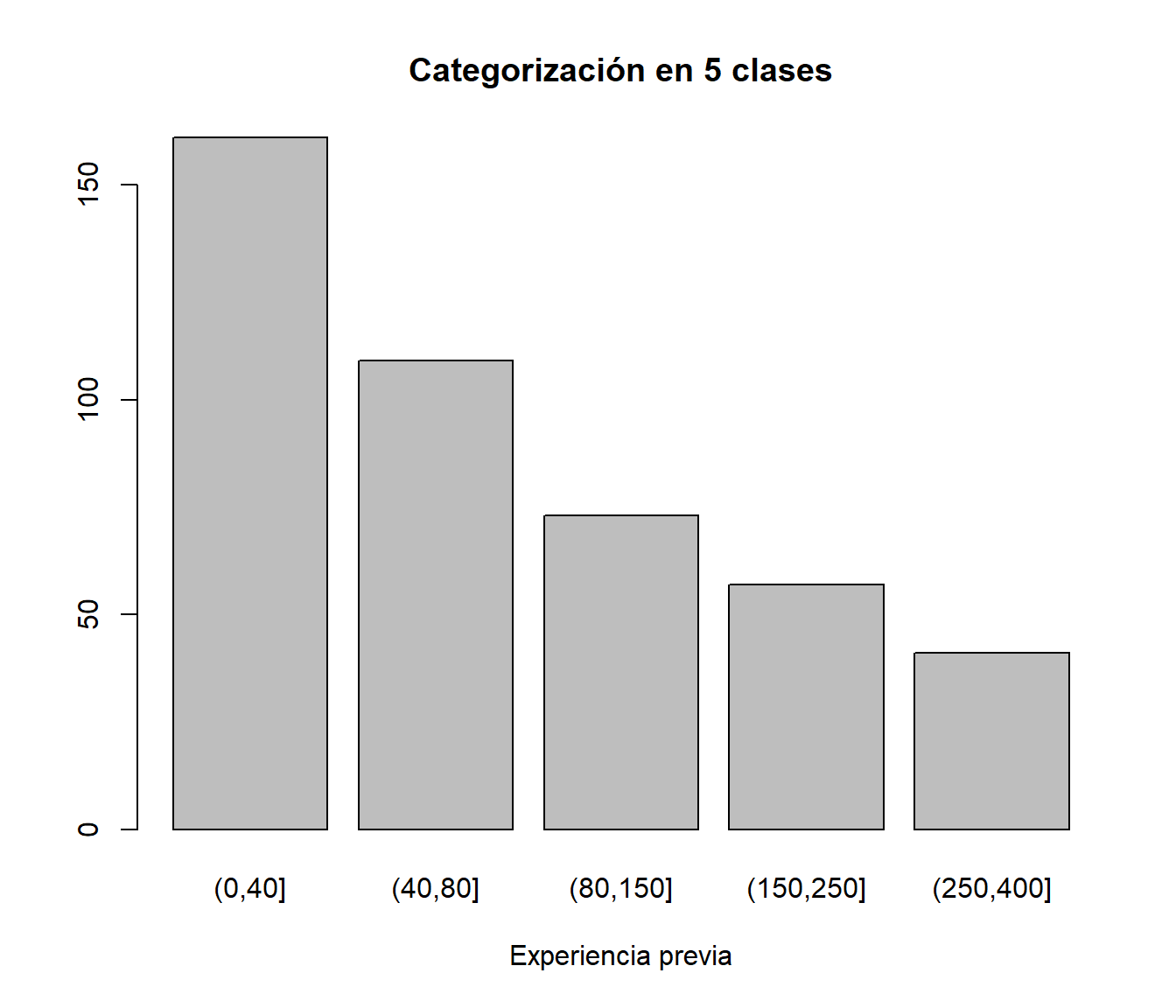

5.2.2 Gráfico de puntos

dotchart(salario, xlab='salarios')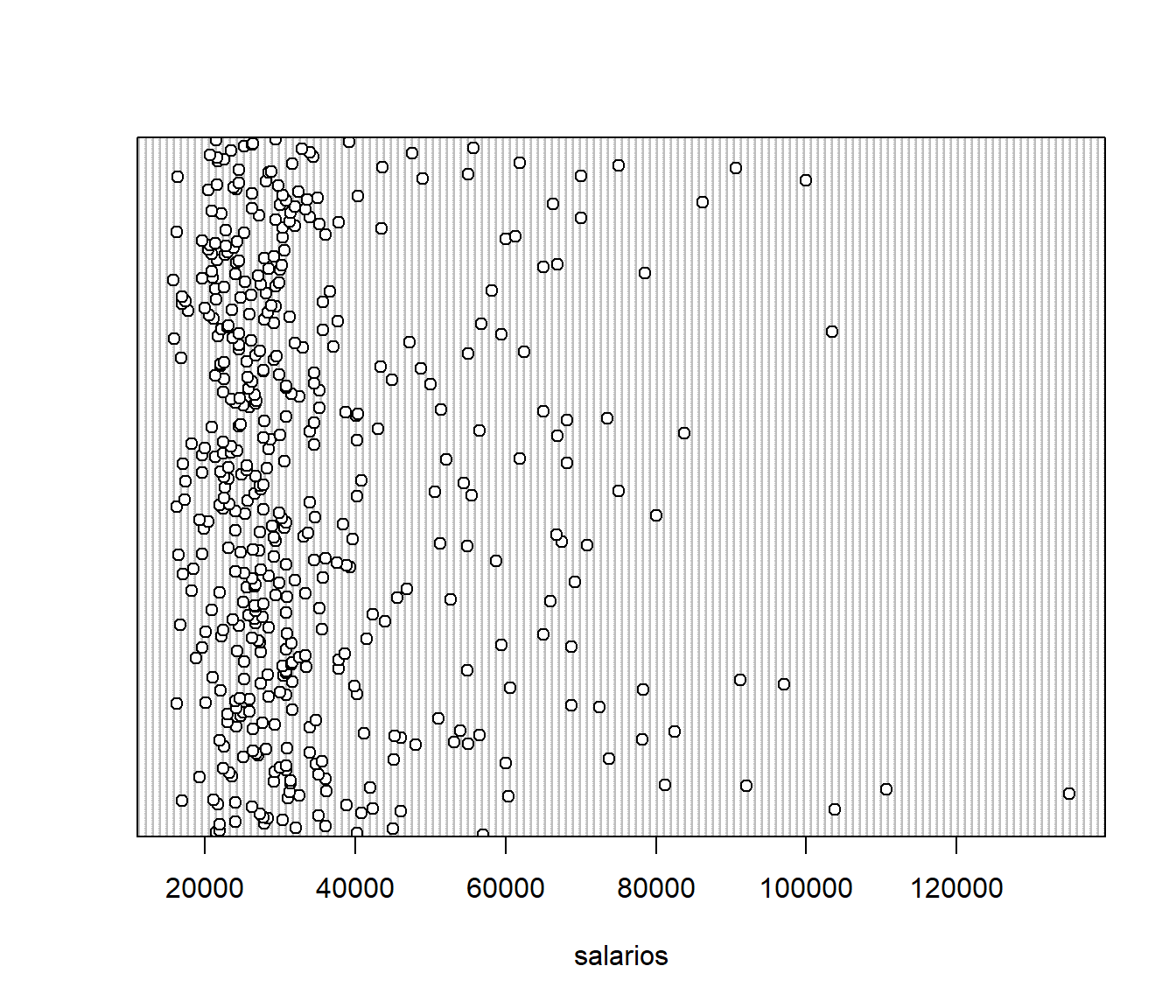

stripchart(salario~sexo, method='jitter')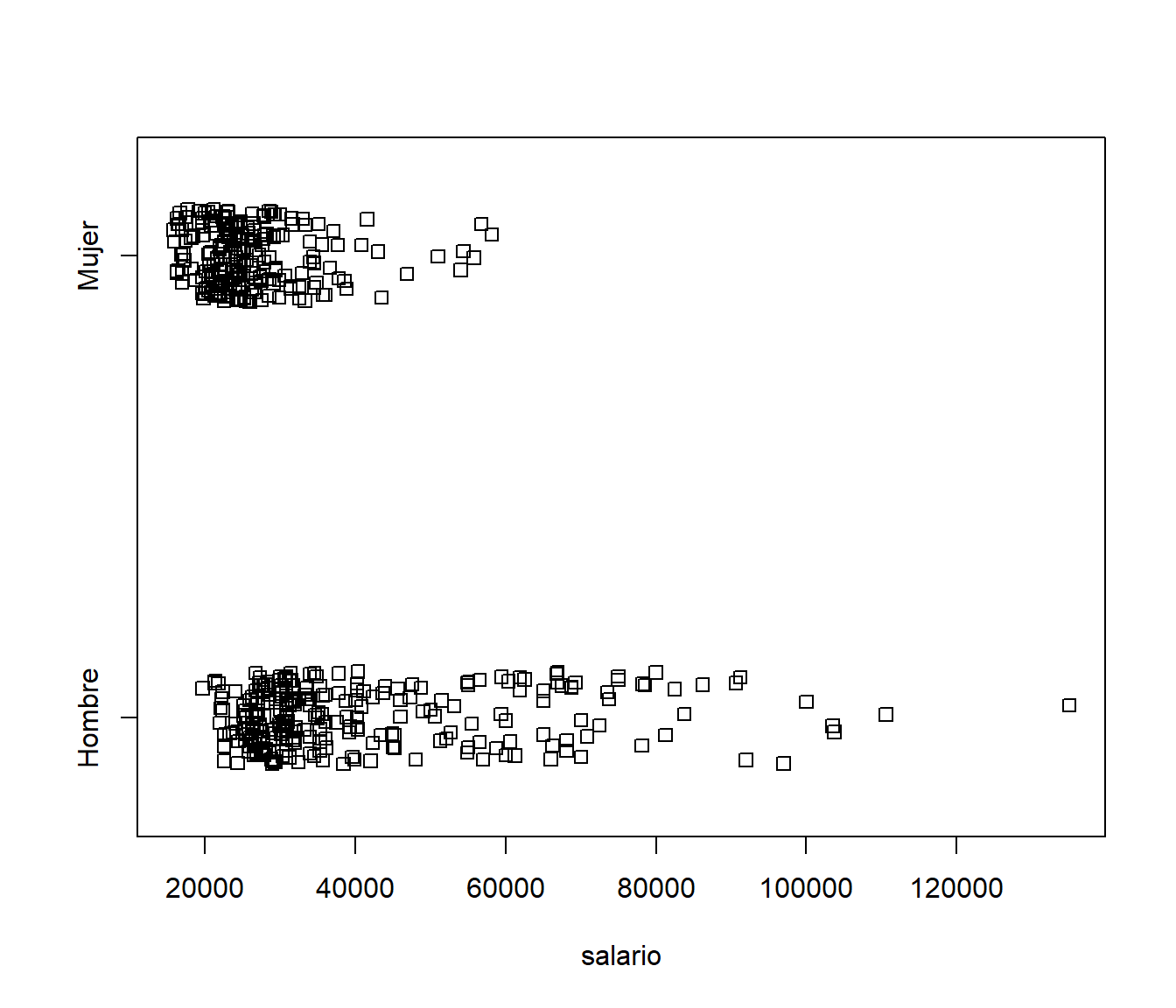

5.2.3 Árbol de tallo y hojas

Esta representación puede ser útil cuando se dispone de pocos datos.

stem(salario)

## 
##   The decimal point is 4 digit(s) to the right of the |
## 
##    1 | 666666777777777778888999
##    2 | 00000000000000111111111111111111122222222222222222222222233333333333+148
##    3 | 00000000000000000001111111111111111111111111122222222222223333333333+36
##    4 | 0000000001112222334445555666778899
##    5 | 0111123344555556677778999
##    6 | 0001122355566777888999
##    7 | 00134455889
##    8 | 01346
##    9 | 1127
##   10 | 044
##   11 | 1
##   12 | 
##   13 | 5

stem(tiempemp)

## 
##   The decimal point is at the |
## 
##   62 | 000
##   64 | 00000000000000000000000
##   66 | 000000000000000000000000000000000
##   68 | 0000000000000000000000000000000
##   70 | 0000000000000000
##   72 | 00000000000000000000000000
##   74 | 000000000000000
##   76 | 00000000000000000000000
##   78 | 000000000000000000000000000000000000
##   80 | 00000000000000000000000000000000000000
##   82 | 0000000000000000000000000000000000
##   84 | 000000000000000000000000
##   86 | 000000000000000000000000
##   88 | 00000000000000000000
##   90 | 00000000000000000000000000000
##   92 | 00000000000000000000000000000000000000
##   94 | 00000000000000000000
##   96 | 000000000000000000000000000
##   98 | 00000000000000

5.2.4 Histograma

Este gráfico es uno de los más habituales para representar datos continuos

hist(salario, main='número de clases por defecto')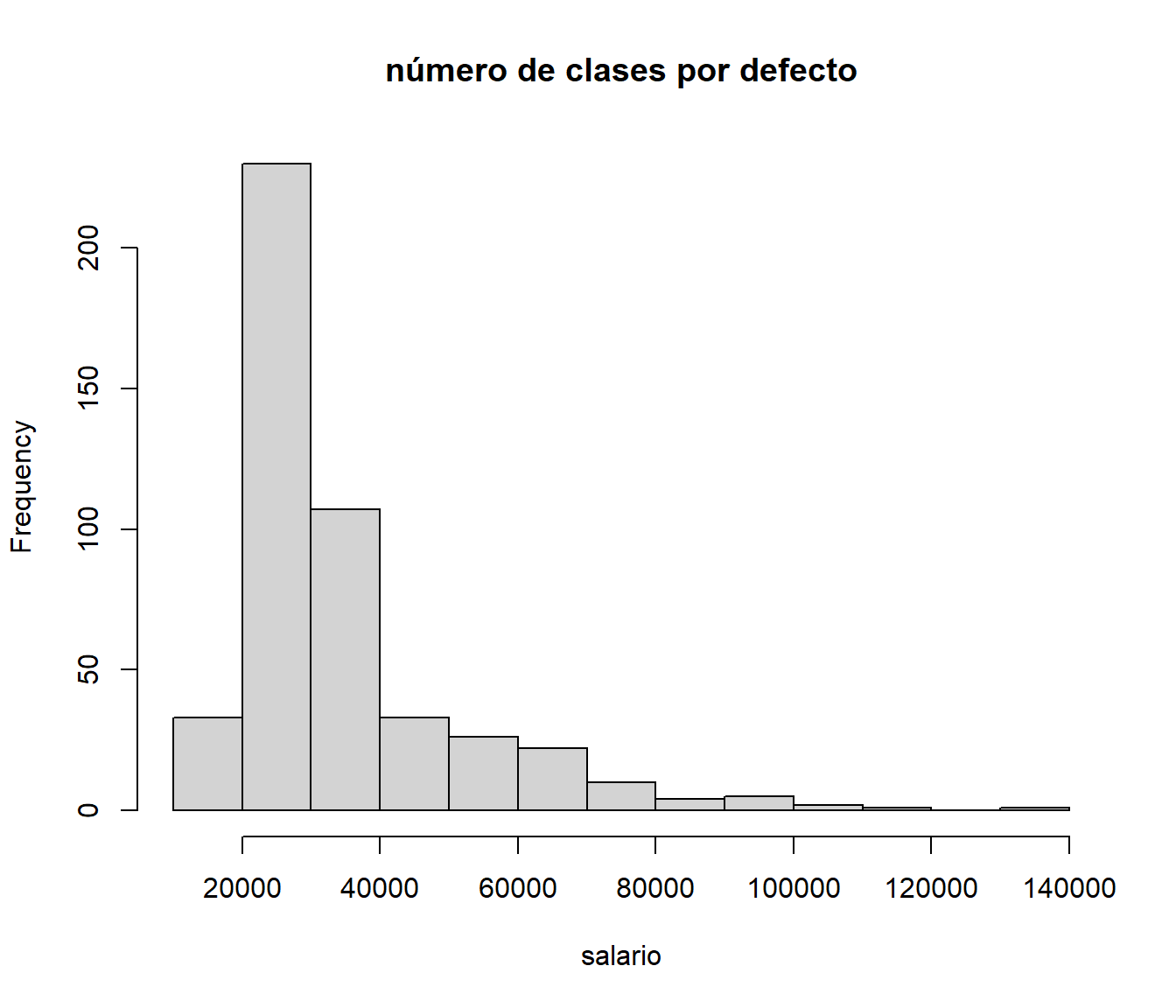

hist(salario, breaks=3, main='3 intervalos de clase')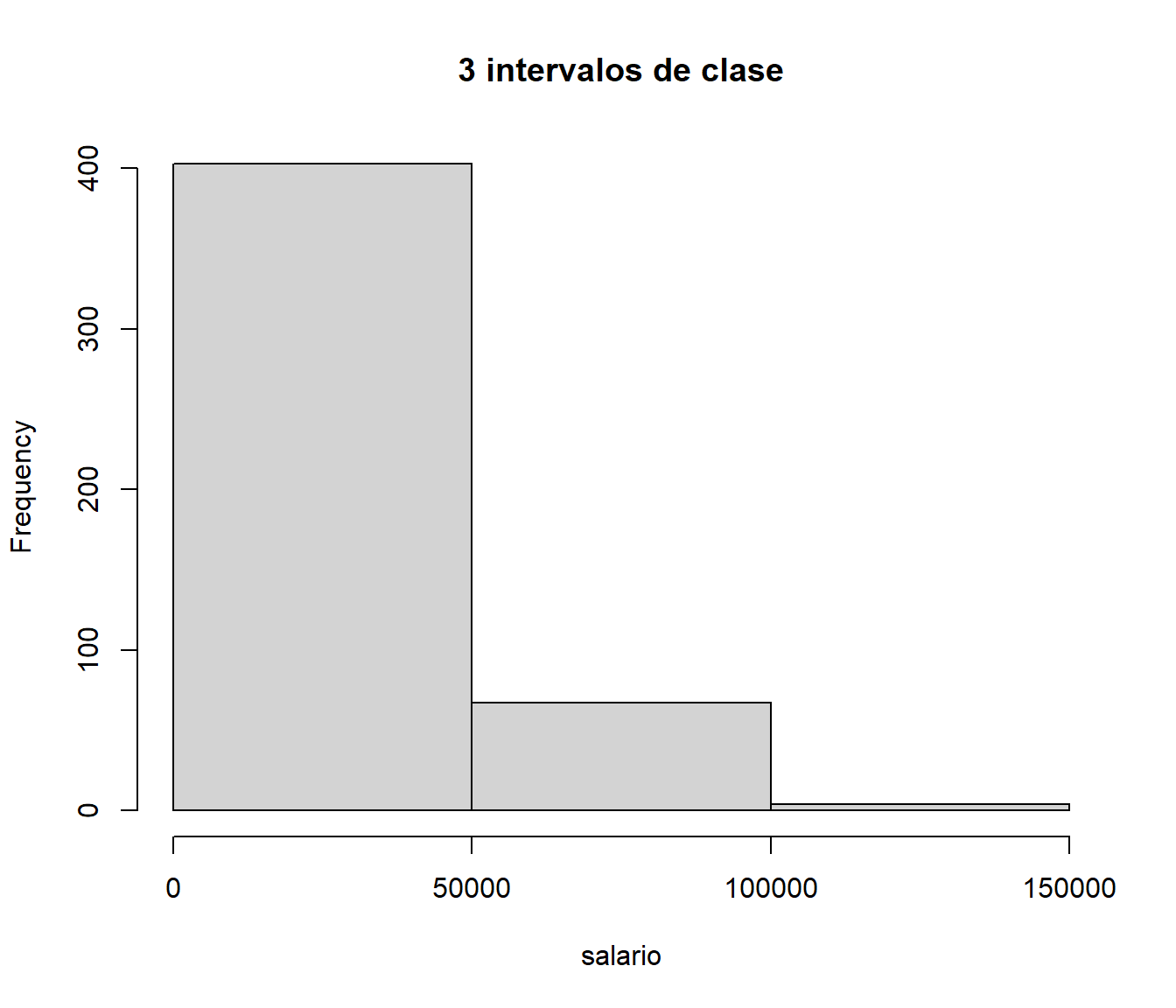

hist(salario, breaks=100, main='100 intervalos de clase')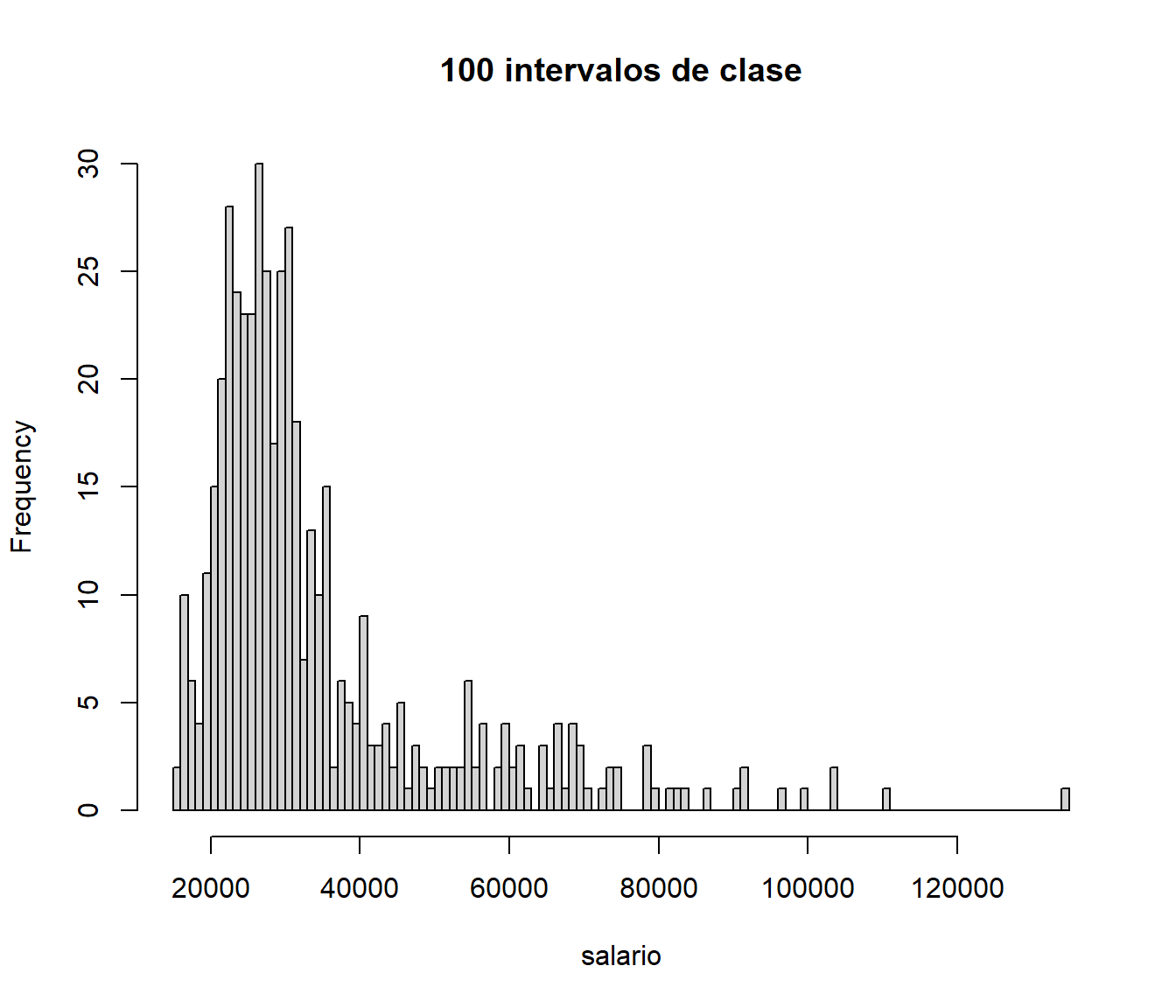

cl1 <- seq(15000,40000,5000)
cl2 <- seq(50000,80000,10000)
cl3 <- seq(100000,140000,20000)
hist(salario, breaks=c(cl1,cl2,cl3),main='intervalos de clase de distinta amplitud')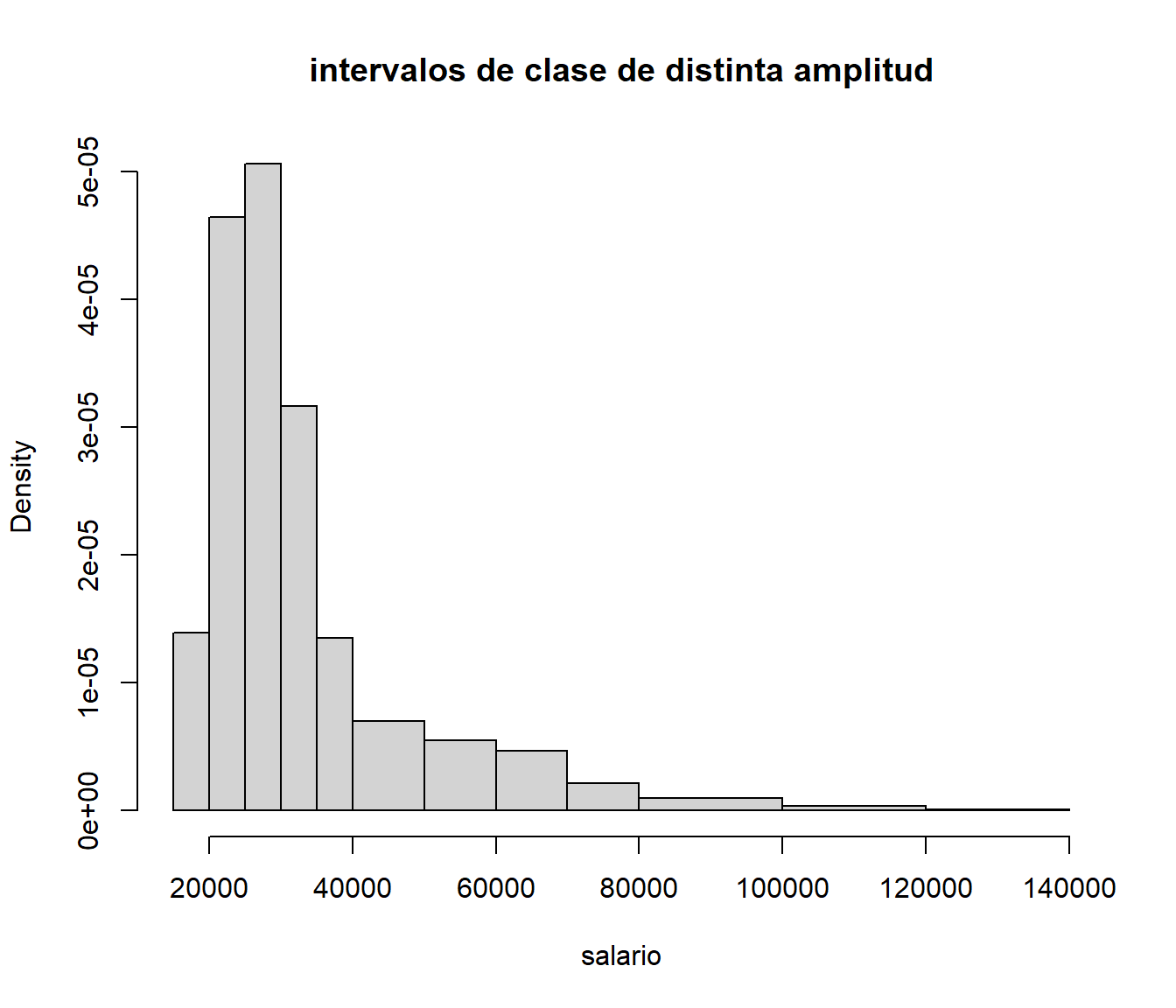

5.2.5 Gráfico de densidad

Es una versión suavizada del histograma.

plot(density(salario))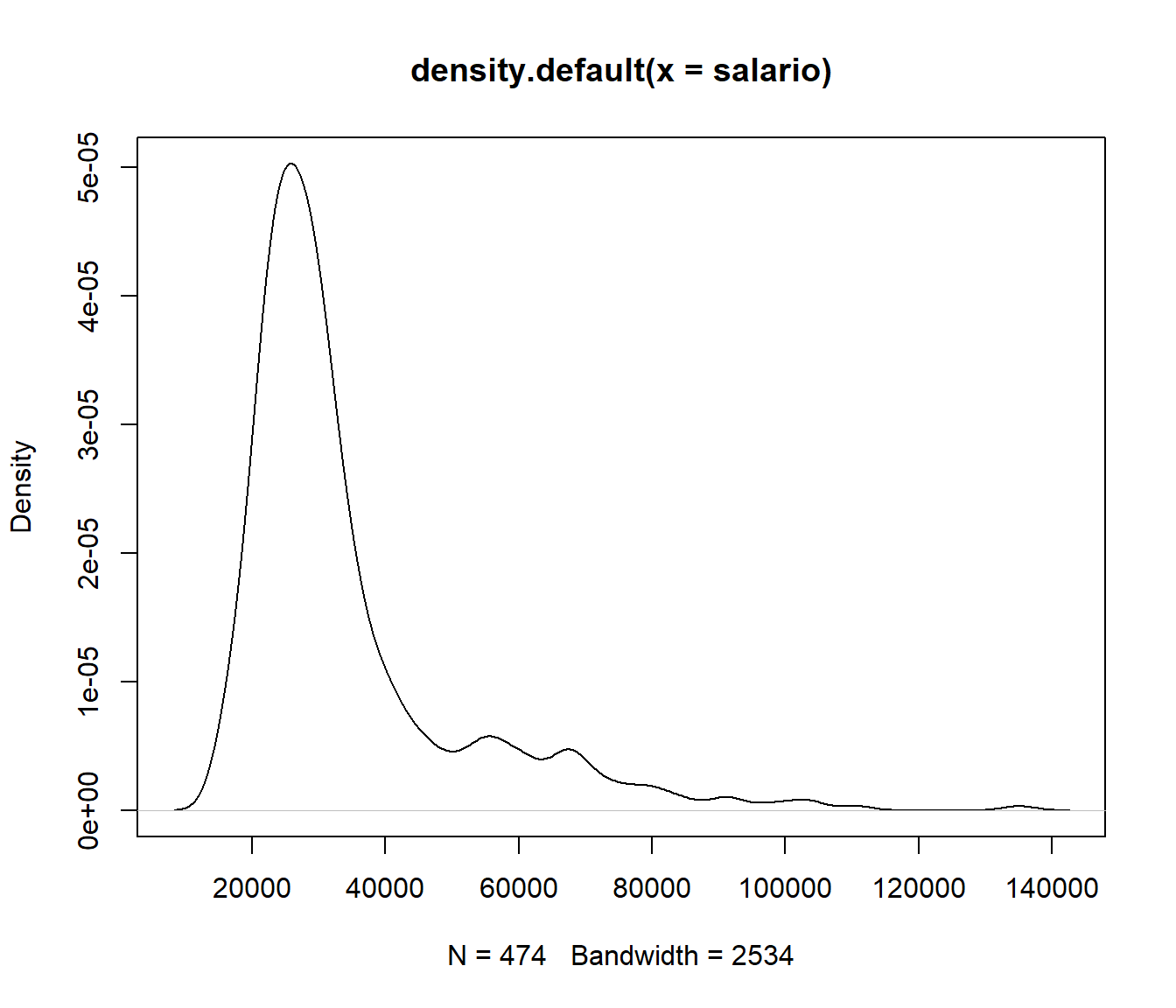

hist(salario, freq=F, main='')
lines(density(salario), lwd=3, col='red')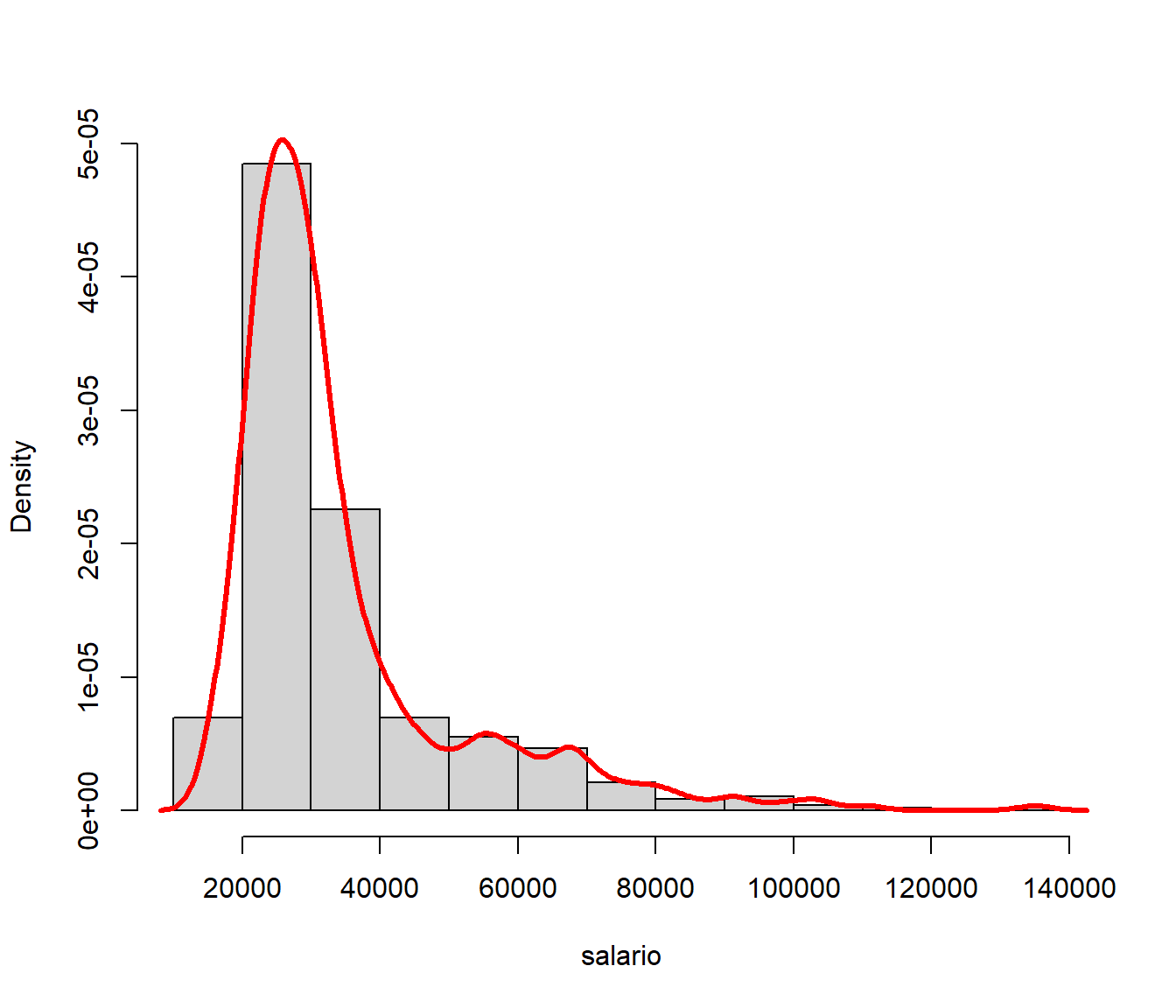

El paquete car nos da acceso a la instrucción densityPlot:

library(car)  # help(car)
densityPlot(salario~sexo)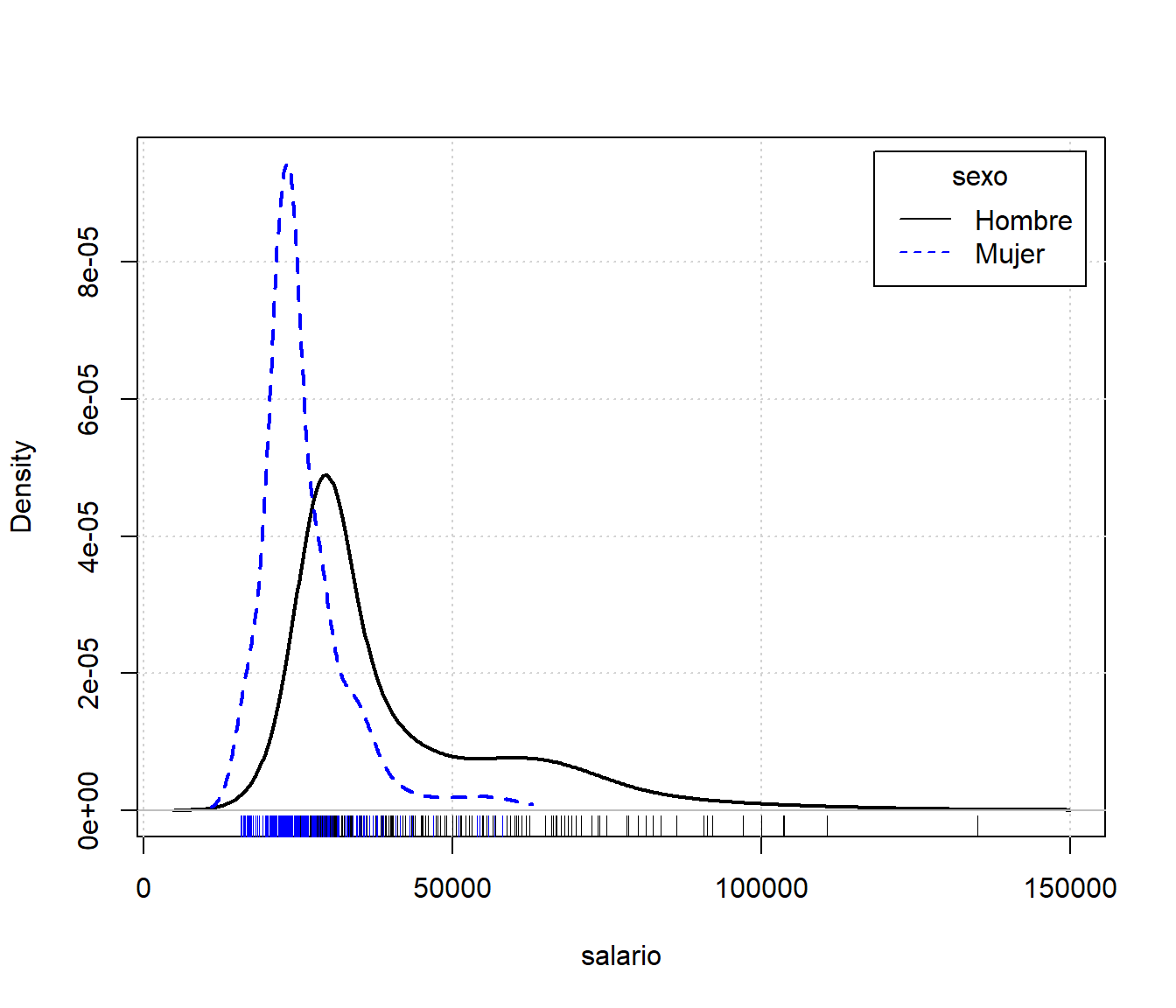

5.2.6 Diagrama de cajas

Se trata de un gráfico muy polivalente

boxplot(salario, horizontal=T, axes=F)
axis(1)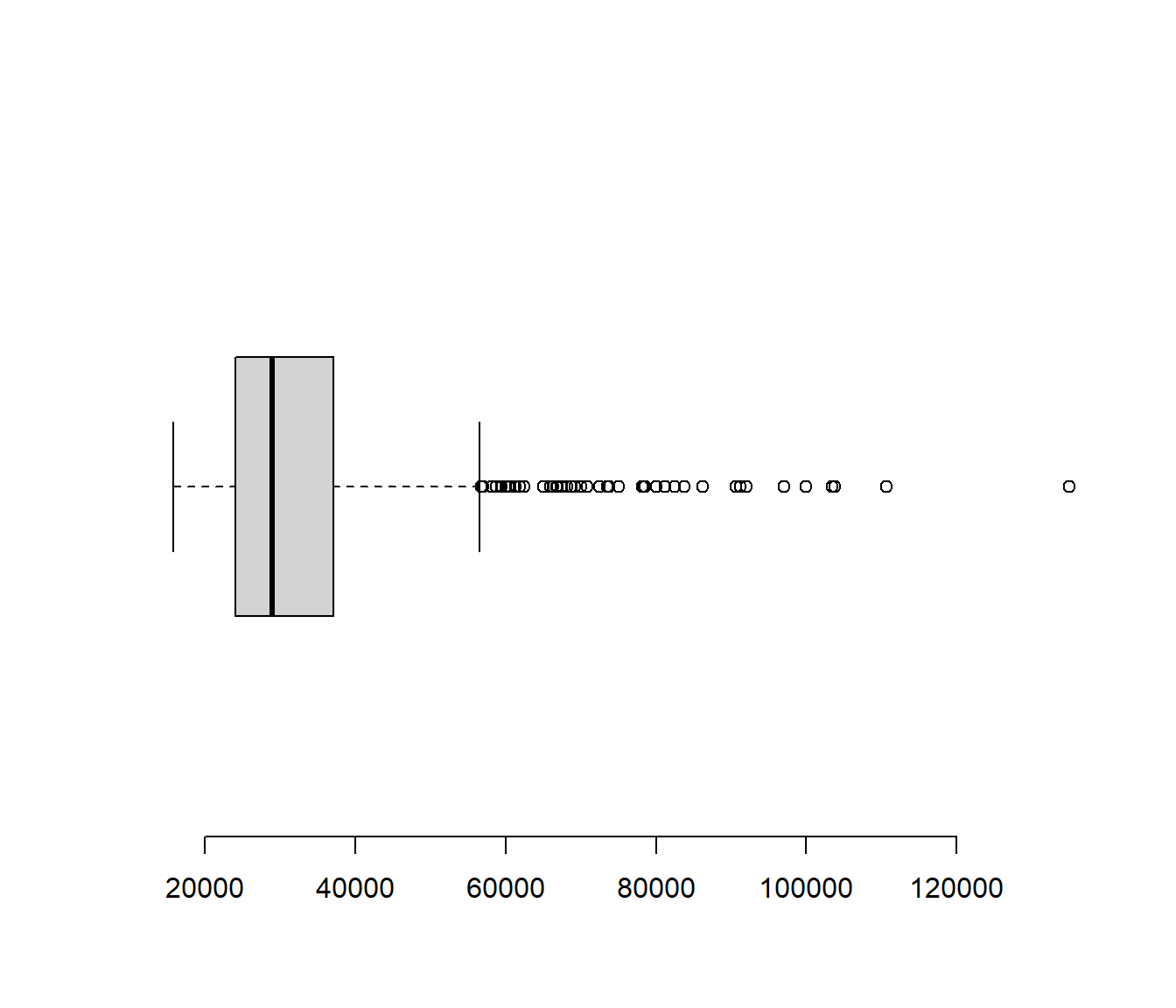

par(mfrow=c(1,2))
boxplot(salario~catlab)
boxplot(salario~sexo)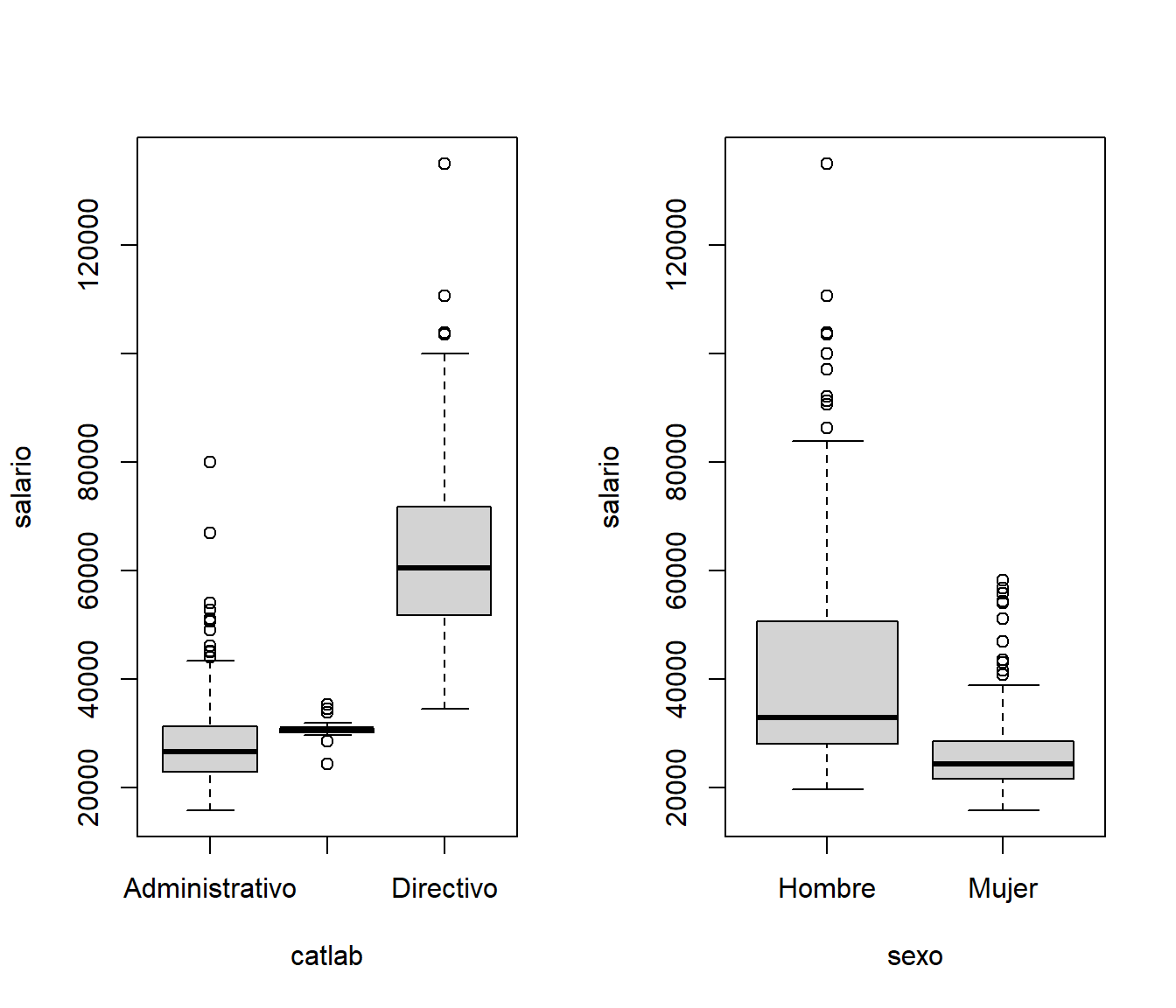

par(mfrow=c(1,1))
boxplot(salario~sexo*catlab)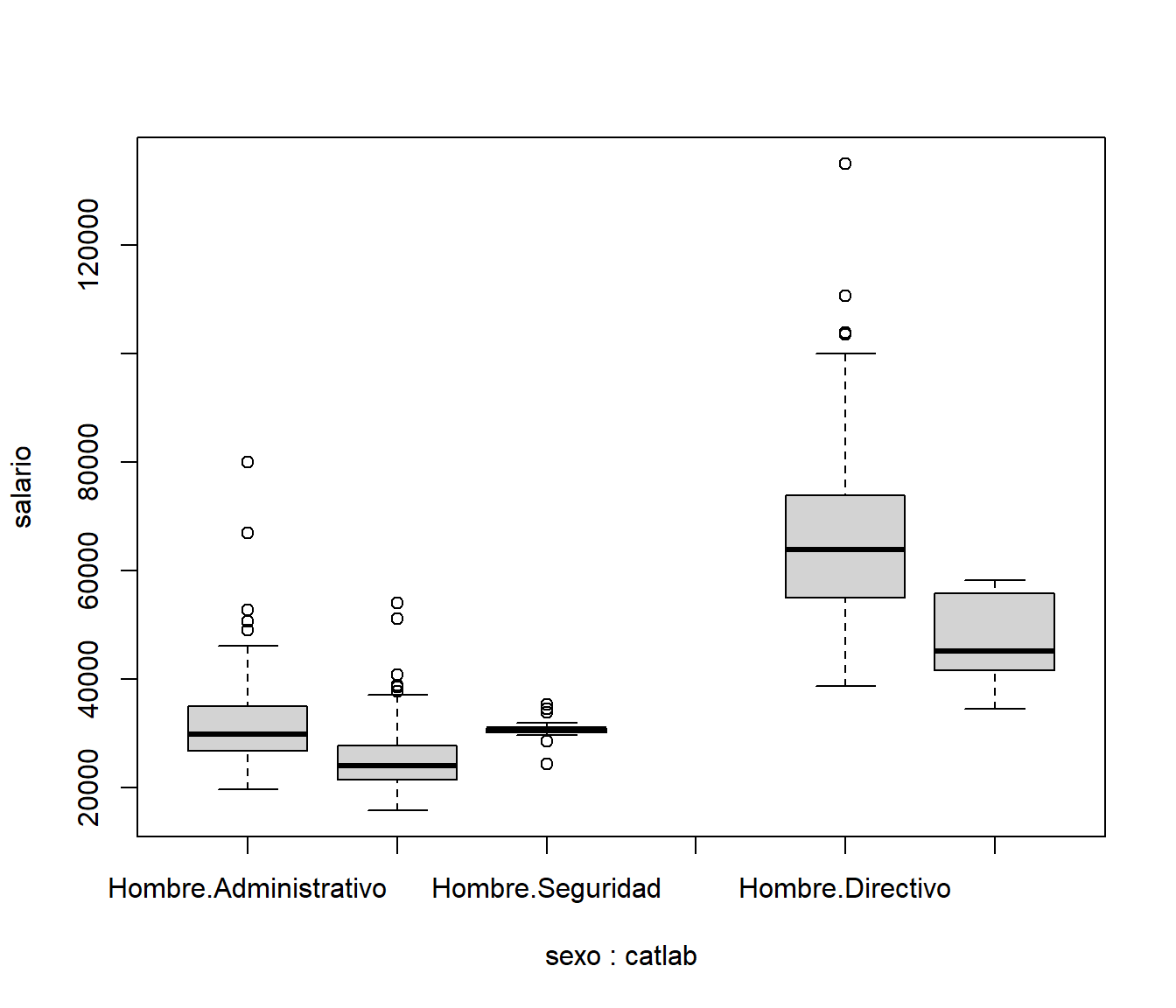

boxplot(salini, salario)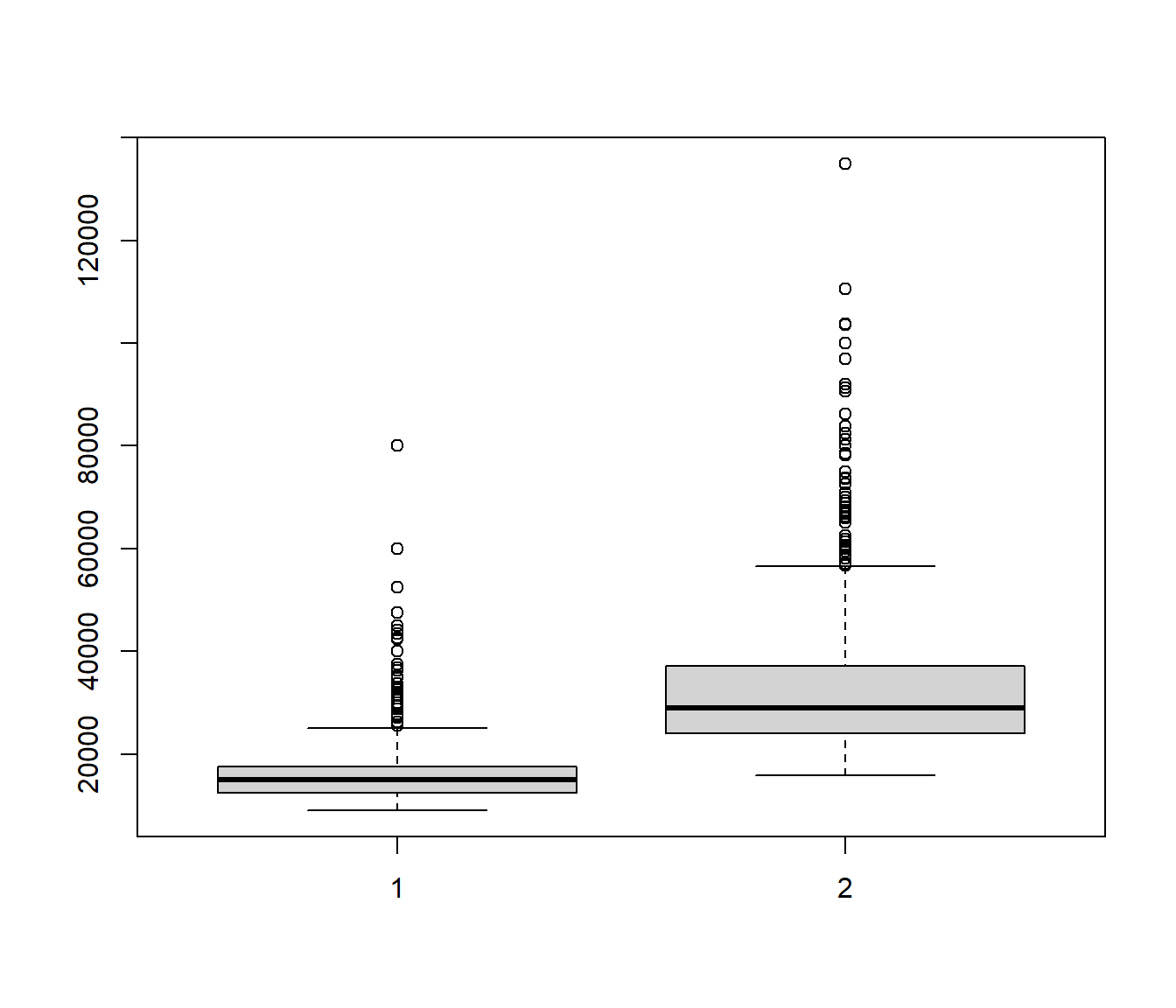

hist(salario,probability=T,ylab="",col='grey',axes=F,main=""); axis(1)
lines(density(salario),col='red',lwd=2)
par(new=T)
boxplot(salario,horizontal=T,axes=F,lwd=2)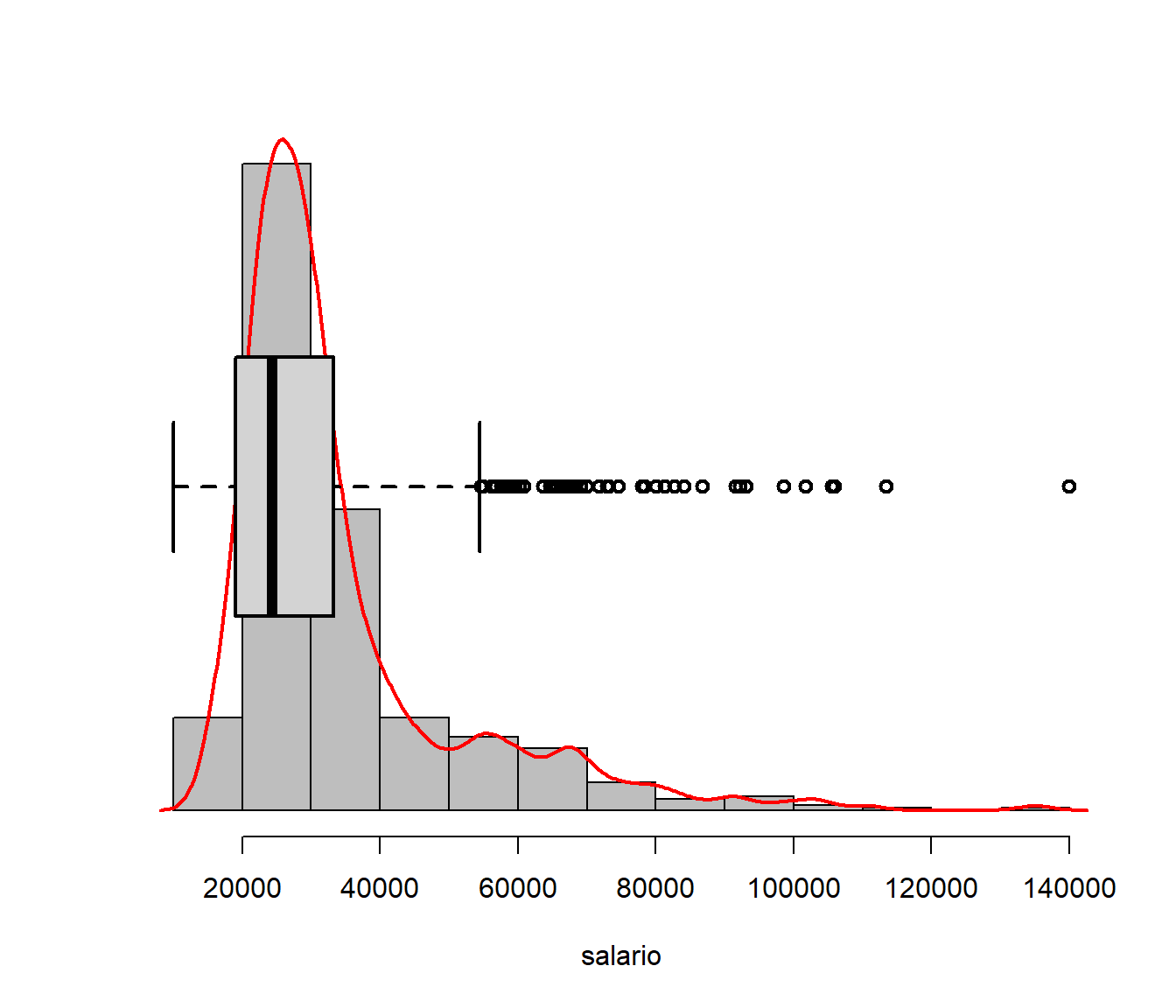

5.2.7 Gráfica de dispersión

Permite ver la relación entre dos variables:

plot(educ,salario)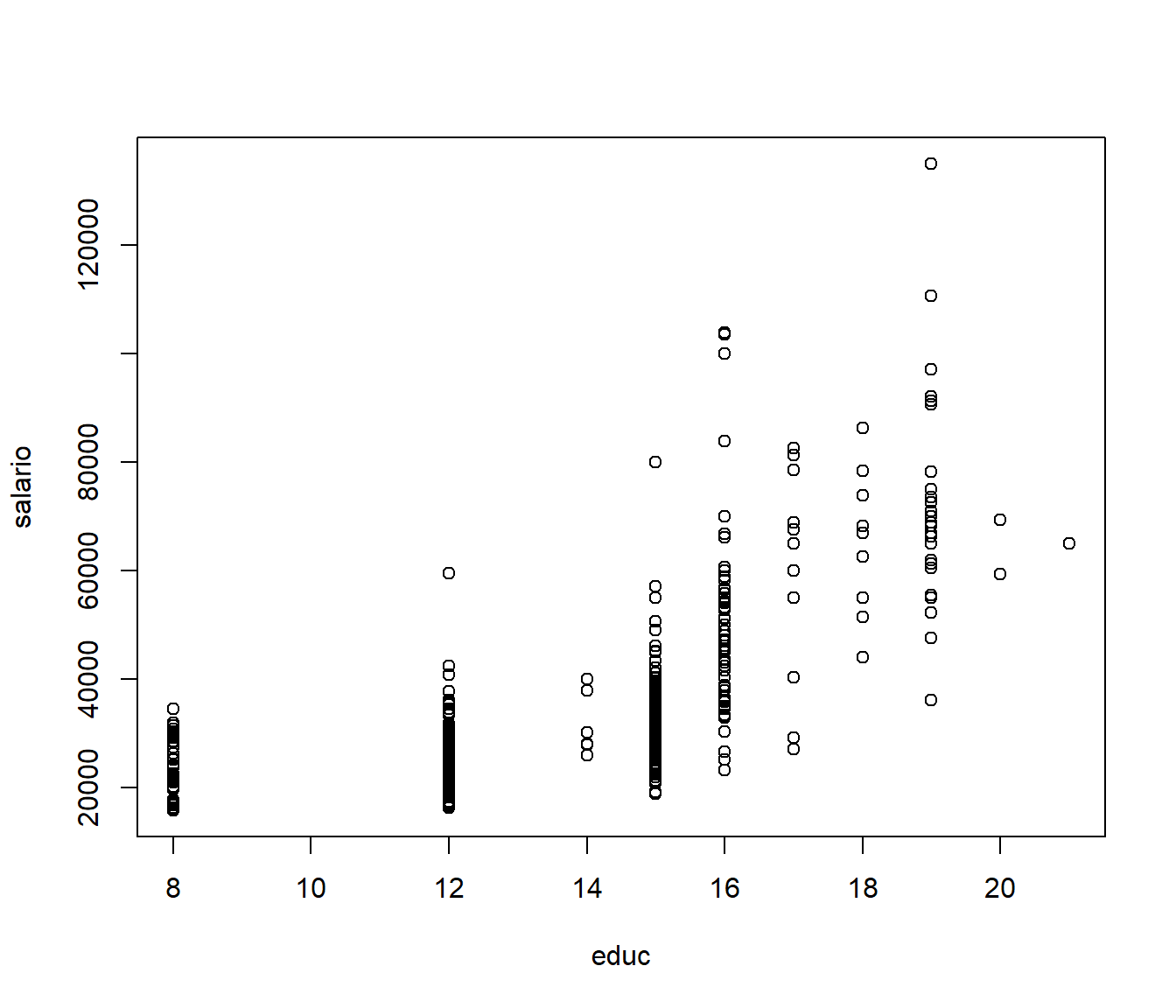

plot(tiempemp,salario)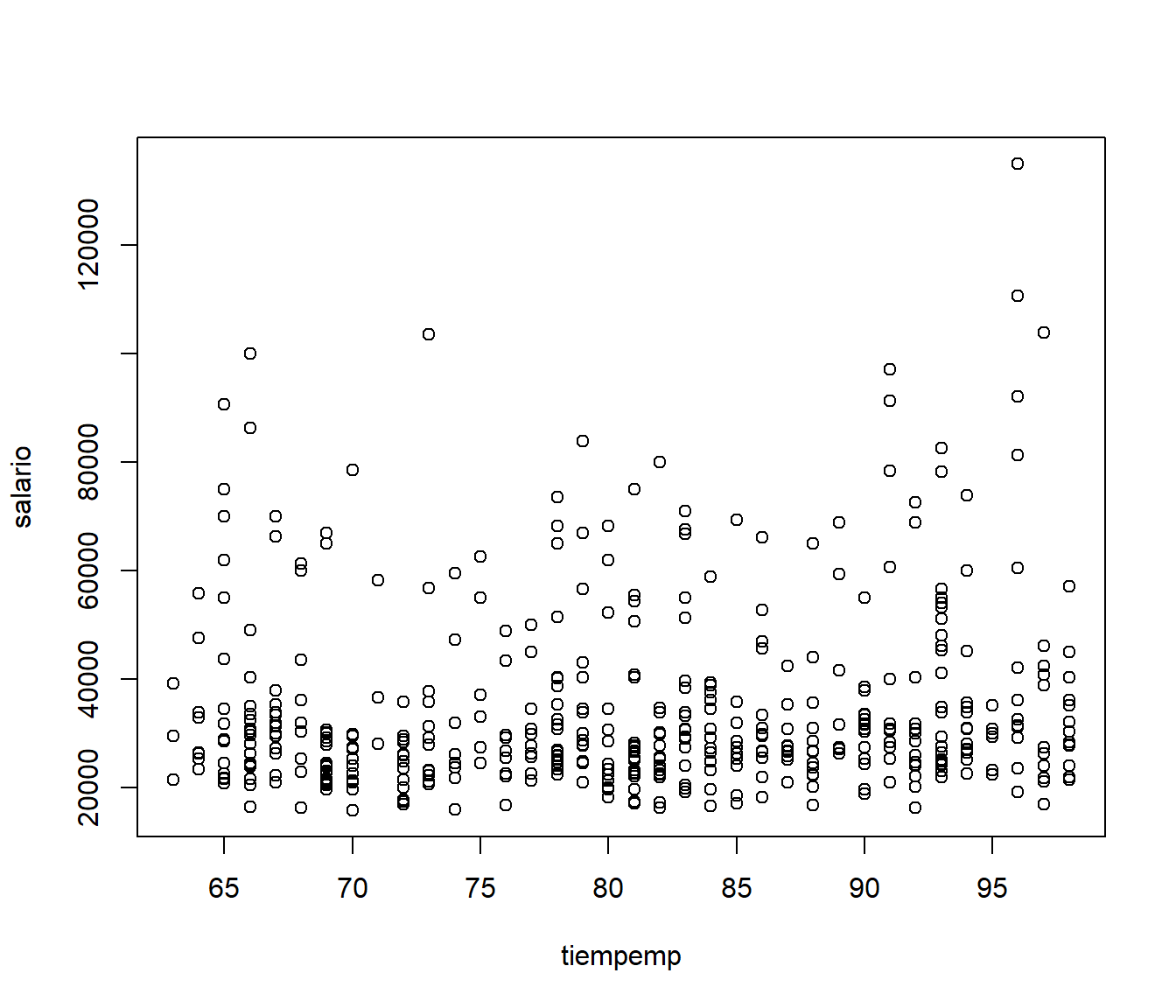

plot(salini,salario)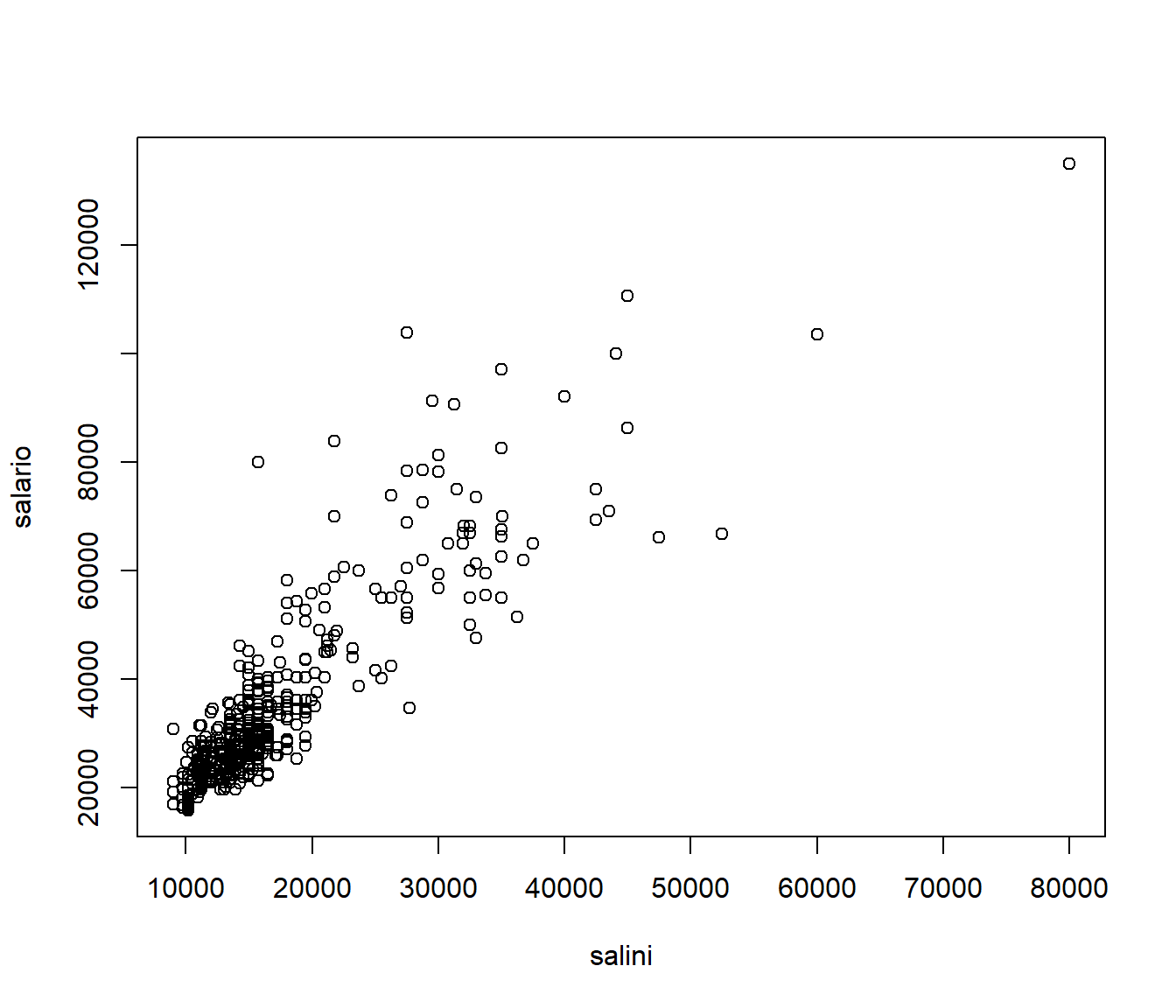

En el caso de una serie temporal

AirPassengers

##      Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
## 1949 112 118 132 129 121 135 148 148 136 119 104 118
## 1950 115 126 141 135 125 149 170 170 158 133 114 140
## 1951 145 150 178 163 172 178 199 199 184 162 146 166
## 1952 171 180 193 181 183 218 230 242 209 191 172 194
## 1953 196 196 236 235 229 243 264 272 237 211 180 201
## 1954 204 188 235 227 234 264 302 293 259 229 203 229
## 1955 242 233 267 269 270 315 364 347 312 274 237 278
## 1956 284 277 317 313 318 374 413 405 355 306 271 306
## 1957 315 301 356 348 355 422 465 467 404 347 305 336
## 1958 340 318 362 348 363 435 491 505 404 359 310 337
## 1959 360 342 406 396 420 472 548 559 463 407 362 405
## 1960 417 391 419 461 472 535 622 606 508 461 390 432

plot(AirPassengers)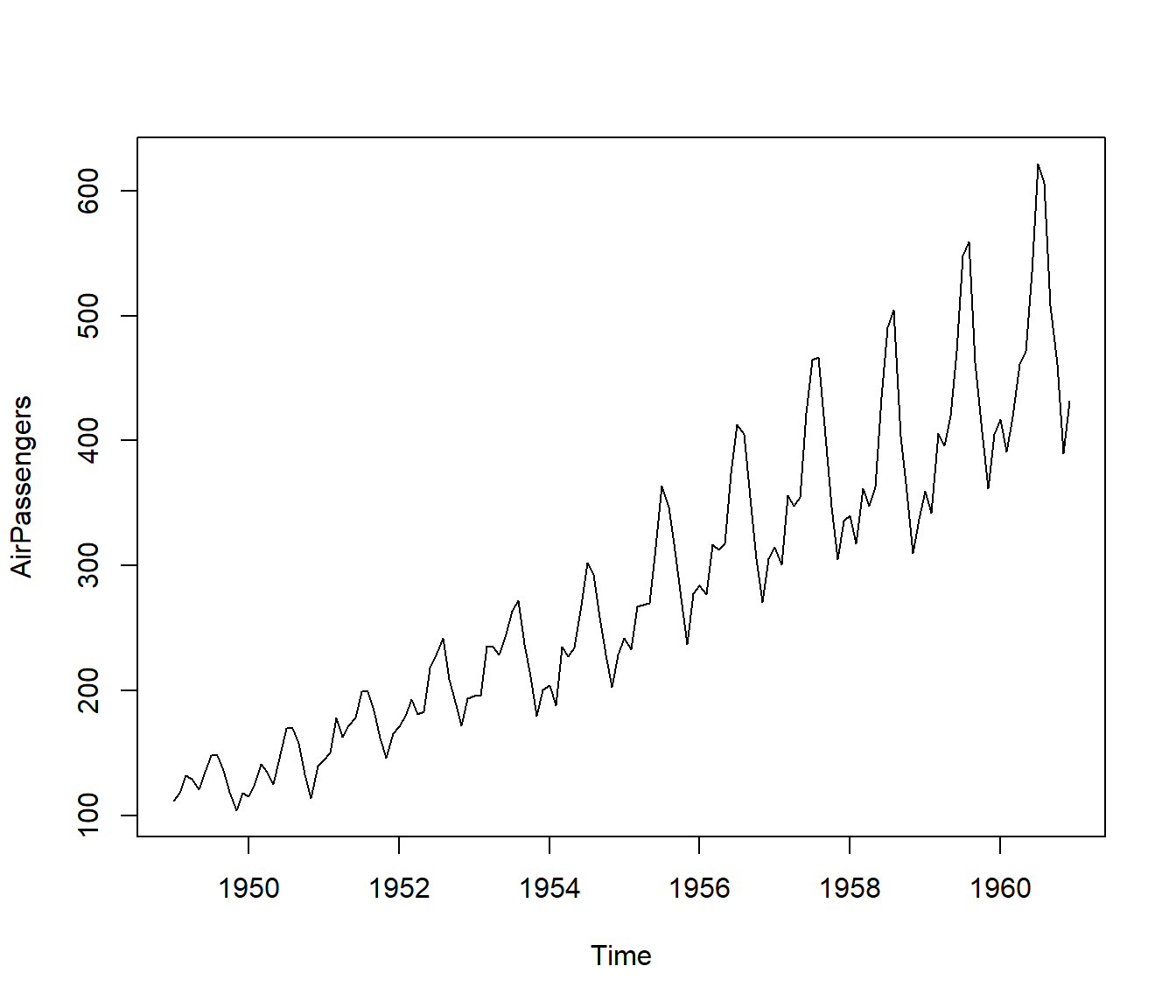

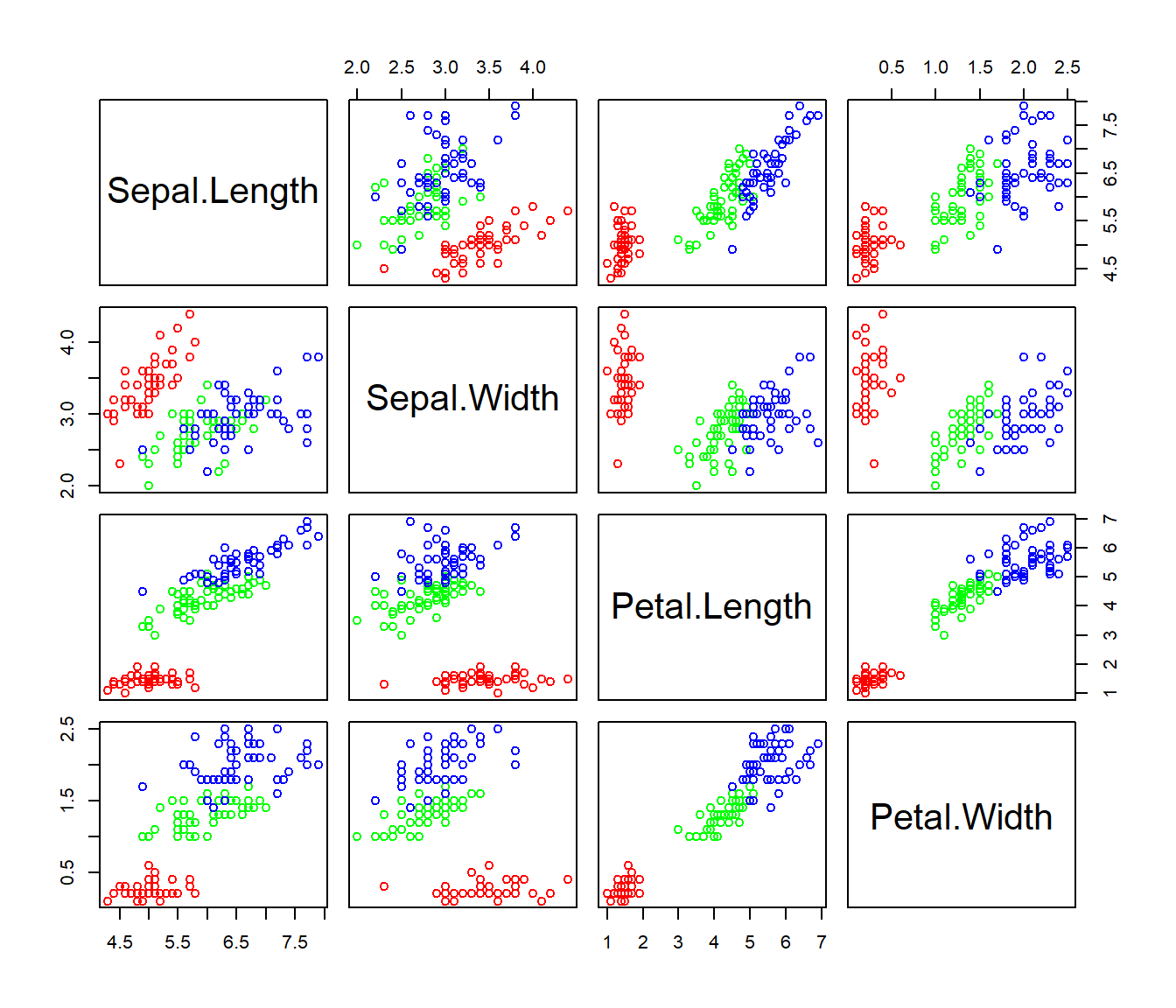
Y un último ejemplo utilizando los datos iris de Fisher:

plot(iris[,3],iris[,4],main="Longitud y anchura de pétalos de lirios",
     xlab="Longitud de pétalo",ylab="Anchura de pétalo")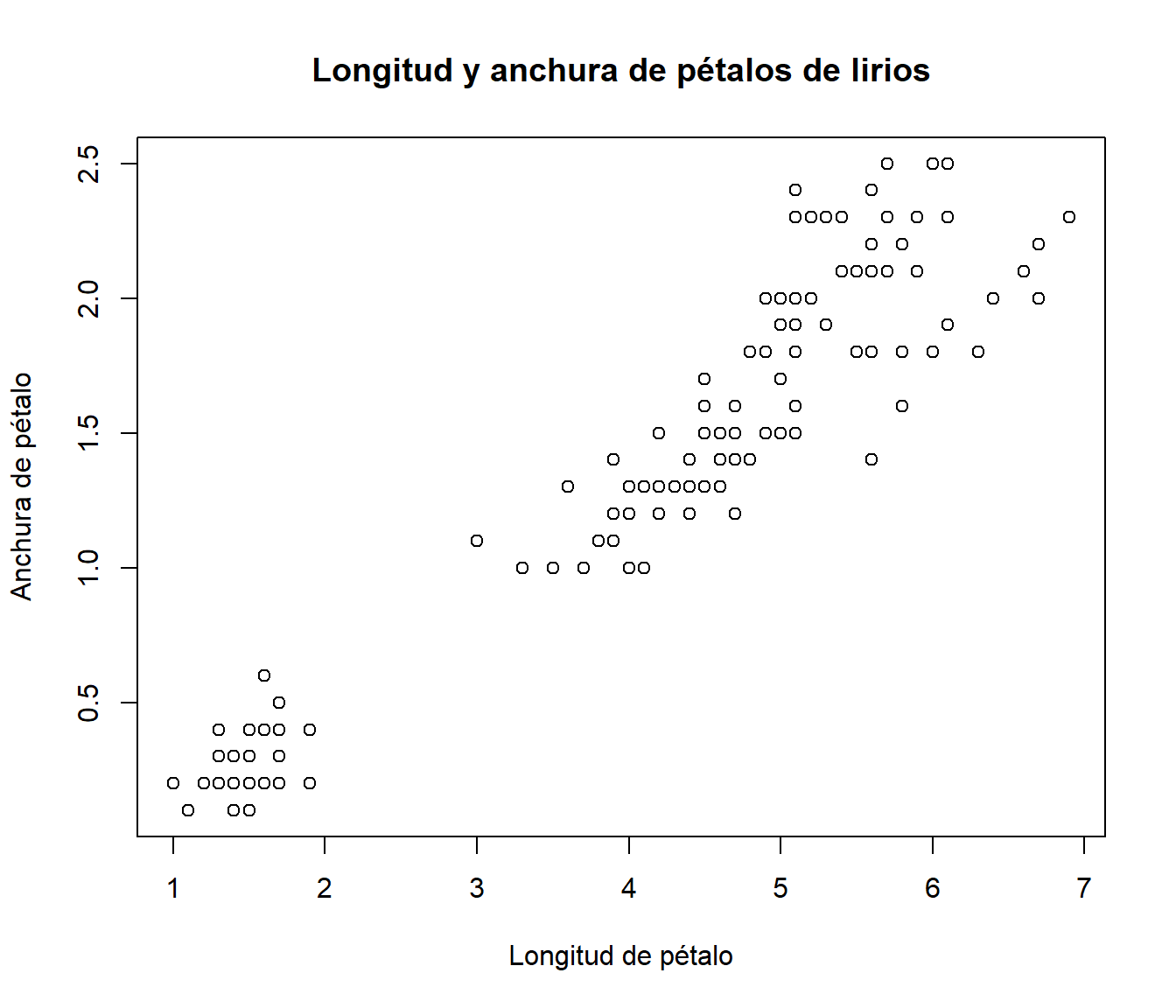

iris.color<-c("red","green","blue")[iris$Species]
plot(iris[,3],iris[,4],col=iris.color,main="Longitud y anchura
     de pétalo según especies",xlab="Longitud de pétalo",
     ylab="Anchura de pétalo")
legend("topleft",c("Setosa","Versicolor","Virginica"),pch=1,
       col=c("red","green","blue"),box.lty=0)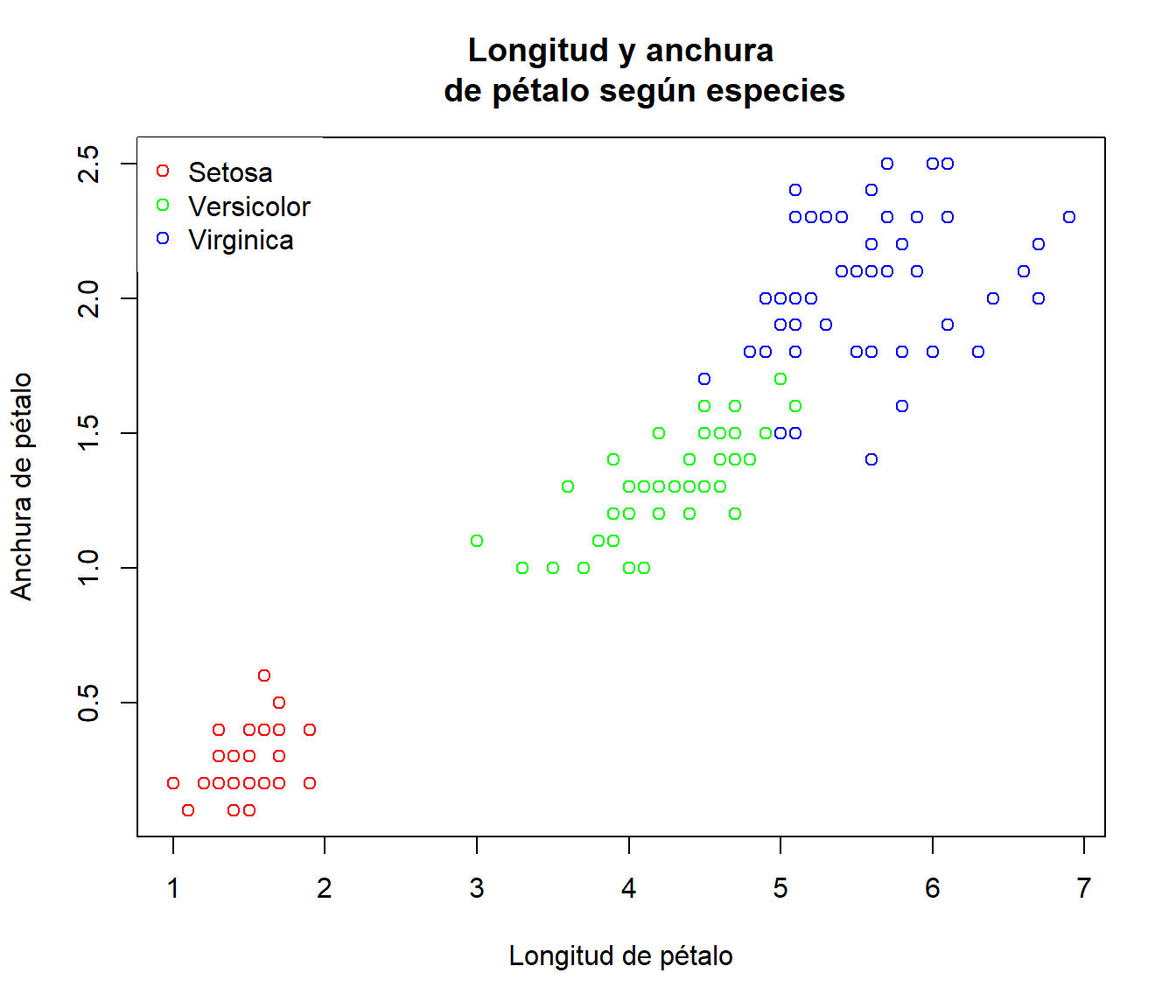

pairs(iris[,1:4],col=iris.color)