8.6 Interacciones

Al emplear el operador + se considera que los efectos de las covariables son aditivos (independientes):

modelo <- lm(lnsal ~ lnsalini + catlab, datos)
anova(modelo)

## Analysis of Variance Table
## 
## Response: lnsal
##            Df Sum Sq Mean Sq  F value    Pr(>F)    
## lnsalini    1 58.668  58.668 1901.993 < 2.2e-16 ***
## catlab      2  1.509   0.755   24.465 7.808e-11 ***
## Residuals 470 14.497   0.031                       
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

plot(lnsal ~ lnsalini, data = datos, pch = as.numeric(catlab), col = 'darkgray')
parest <- coef(modelo)
abline(a = parest[1], b = parest[2], lty = 1)
abline(a = parest[1] + parest[3], b = parest[2], lty = 2)
abline(a = parest[1] + parest[4], b = parest[2], lty = 3)
legend("bottomright", levels(datos$catlab), pch = 1:3, lty = 1:3)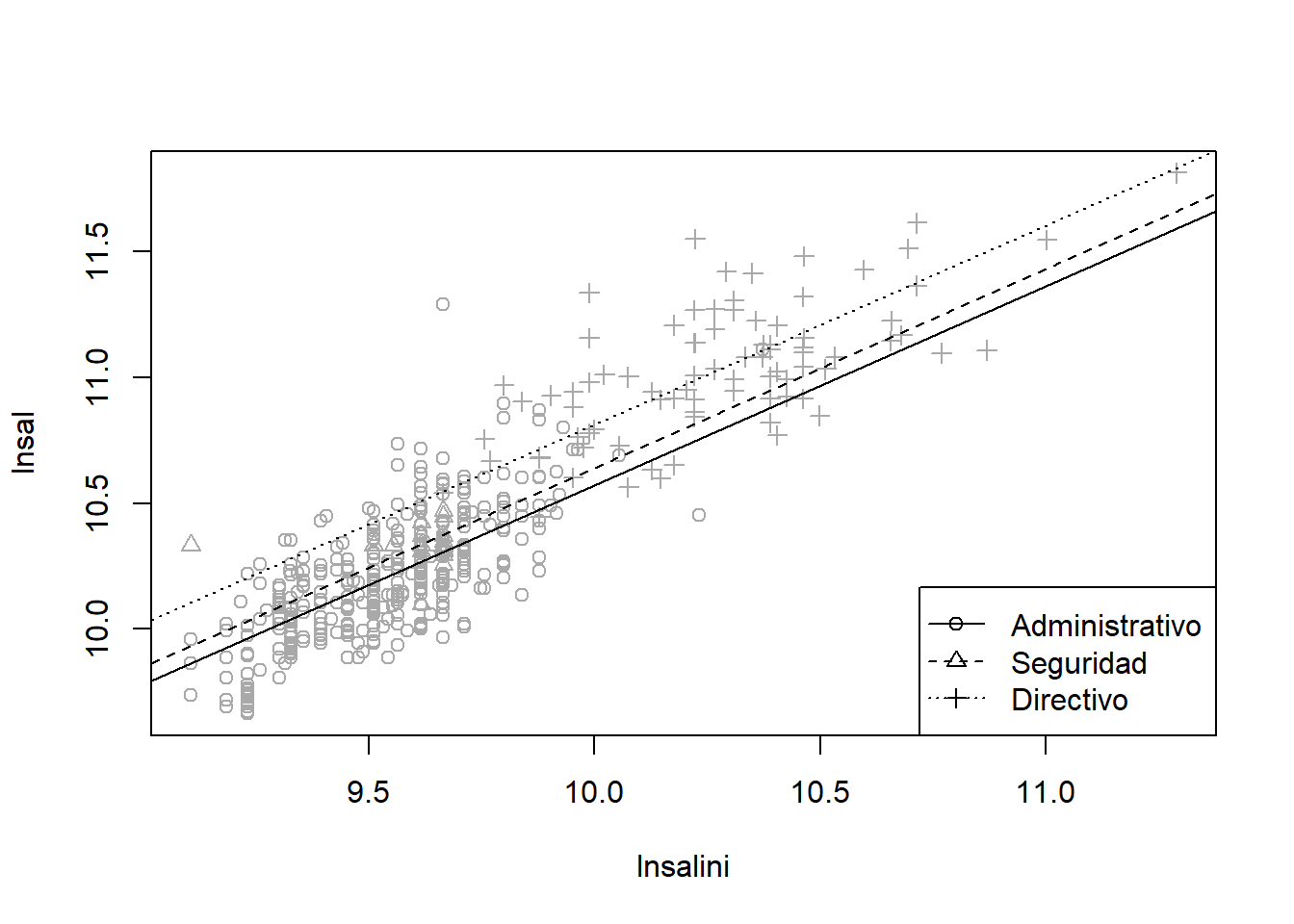

Para especificar que el efecto de una covariable depende de otra (interacción), se pueden emplear los operadores * ó :.

modelo2 <- lm(lnsal ~ lnsalini*catlab, datos)
summary(modelo2)

## 
## Call:
## lm(formula = lnsal ~ lnsalini * catlab, data = datos)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.37440 -0.11335 -0.00524  0.10459  0.97018 
## 
## Coefficients:
##                          Estimate Std. Error t value Pr(>|t|)    
## (Intercept)               1.66865    0.43820   3.808 0.000159 ***
## lnsalini                  0.89512    0.04595  19.479  < 2e-16 ***
## catlabSeguridad           8.31808    3.01827   2.756 0.006081 ** 
## catlabDirectivo           3.01268    0.79509   3.789 0.000171 ***
## lnsalini:catlabSeguridad -0.85864    0.31392  -2.735 0.006470 ** 
## lnsalini:catlabDirectivo -0.27713    0.07924  -3.497 0.000515 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1727 on 468 degrees of freedom
## Multiple R-squared:  0.8131, Adjusted R-squared:  0.8111 
## F-statistic: 407.3 on 5 and 468 DF,  p-value: < 2.2e-16

anova(modelo2)

## Analysis of Variance Table
## 
## Response: lnsal
##                  Df Sum Sq Mean Sq   F value    Pr(>F)    
## lnsalini          1 58.668  58.668 1967.6294 < 2.2e-16 ***
## catlab            2  1.509   0.755   25.3090 3.658e-11 ***
## lnsalini:catlab   2  0.543   0.272    9.1097 0.0001315 ***
## Residuals       468 13.954   0.030                        
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

En este caso las pendientes también varían dependiendo del nivel del factor:

plot(lnsal ~ lnsalini, data = datos, pch = as.numeric(catlab), col = 'darkgray')
parest <- coef(modelo2)
abline(a = parest[1], b = parest[2], lty = 1)
abline(a = parest[1] + parest[3], b = parest[2] + parest[5], lty = 2)
abline(a = parest[1] + parest[4], b = parest[2] + parest[6], lty = 3)
legend("bottomright", levels(datos$catlab), pch = 1:3, lty = 1:3)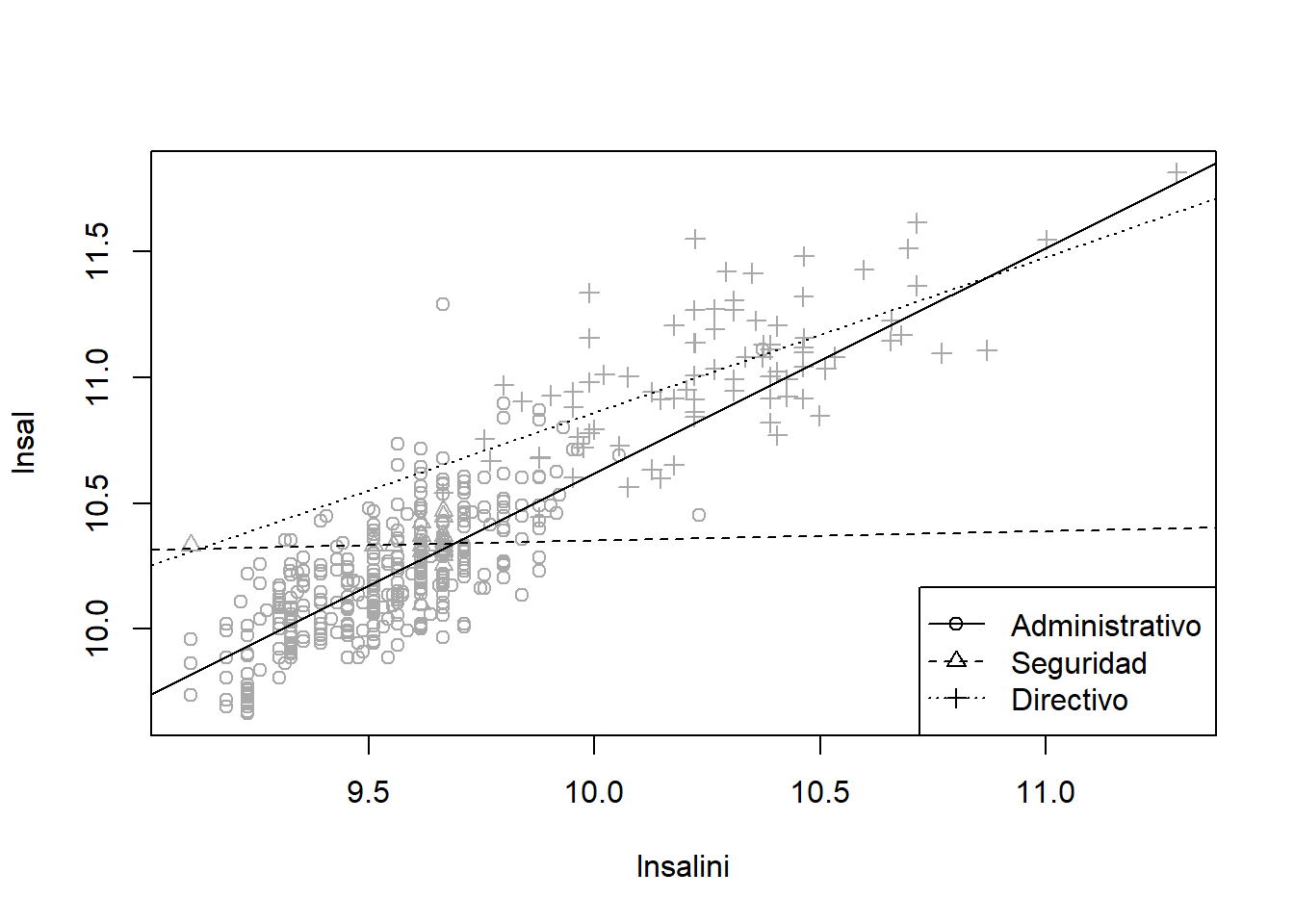

Por ejemplo, empleando la fórmula lnsal ~ lnsalini:catlab se considerarían distintas pendientes pero el mismo término independiente.