8.7 Diagnosis del modelo
Las conclusiones obtenidas con este método se basan en las hipótesis básicas del modelo:
Linealidad.
Normalidad (y homogeneidad).
Homocedasticidad.
Independencia.
Ninguna de las variables explicativas es combinación lineal de las demás.
Si alguna de estas hipótesis no es cierta, las conclusiones obtenidas pueden no ser fiables, o incluso totalmente erróneas. En el caso de regresión múltiple es de especial interés el fenómeno de la multicolinealidad (o colinearidad) relacionado con la última de estas hipótesis.
En esta sección consideraremos como ejemplo el modelo:
modelo <- lm(salario ~ salini + expprev, data = empleados)
summary(modelo) ##
## Call:
## lm(formula = salario ~ salini + expprev, data = empleados)
##
## Residuals:
## Min 1Q Median 3Q Max
## -32263 -4219 -1332 2673 48571
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3850.71760 900.63287 4.276 2.31e-05 ***
## salini 1.92291 0.04548 42.283 < 2e-16 ***
## expprev -22.44482 3.42240 -6.558 1.44e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 7777 on 471 degrees of freedom
## Multiple R-squared: 0.7935, Adjusted R-squared: 0.7926
## F-statistic: 904.8 on 2 and 471 DF, p-value: < 2.2e-168.7.1 Gráficas básicas de diagnóstico
Con la función plot se pueden generar gráficos de interés para la diagnosis del modelo:
oldpar <- par( mfrow=c(2,2))
plot(modelo)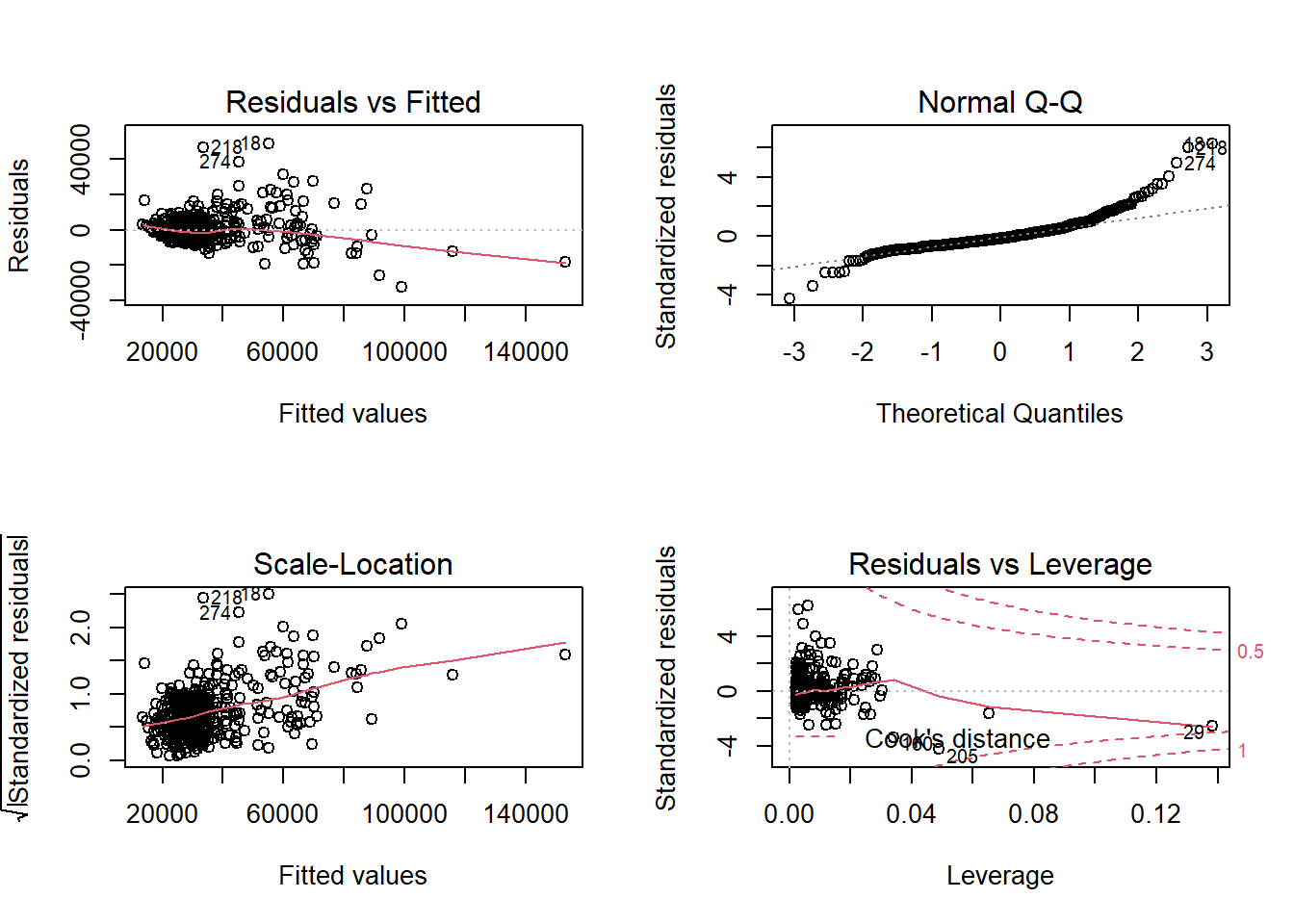
par(oldpar)Por defecto se muestran cuatro gráficos (ver help(plot.lm) para más detalles). El primero (residuos frente a predicciones) permite detectar falta de
linealidad o heterocedasticidad (o el efecto de un factor omitido: mala
especificación del modelo), lo ideal sería no observar ningún patrón.
El segundo gráfico (gráfico QQ), permite diagnosticar la normalidad, los puntos del deberían estar cerca de la diagonal.
El tercer gráfico de dispersión-nivel permite detectar heterocedasticidad y ayudar a seleccionar una transformación para corregirla (más adelante, en la sección Alternativas, se tratará este tema), la pendiente de los datos debería ser nula.
El último gráfico permite detectar valores atípicos o influyentes. Representa los residuos estandarizados en función del valor de influencia (a priori) o leverage (\(hii\) que depende de los valores de las variables explicativas, debería ser \(< 2(p+1)/2\)) y señala las observaciones atípicas (residuos fuera de [-2,2]) e influyentes a posteriori (estadístico de Cook >0.5 y >1).
Si las conclusiones obtenidas dependen en gran medida de una observación (normalmente atípica), esta se denomina influyente (a posteriori) y debe ser examinada con cuidado por el experimentador. Para recalcular el modelo sin una de las observaciones puede ser útil la función update:
# which.max(cooks.distance(modelo))
modelo2 <- update(modelo, data = empleados[-29, ])Si hay datos atípicos o influyentes, puede ser recomendable emplear regresión lineal robusta, por ejemplo mediante la función rlm del paquete MASS.
En el ejemplo anterior, se observa claramente heterogeneidad de varianzas y falta de normalidad. Aparentemente no hay observaciones influyentes (a posteriori) aunque si algún dato atípico.
8.7.2 Gráficos parciales de residuos
En regresión lineal múltiple, en lugar de generar gráficos de dispersión simple (p.e. gráficos de dispersión matriciales) para detectar problemas (falta de linealidad, …) y analizar los efectos de las variables explicativas, se pueden generar gráficos parciales de residuos, por ejemplo con el comando:
termplot(modelo, partial.resid = TRUE)Aunque puede ser preferible emplear las funciones crPlots ó avPlots del paquete car:
library(car)
crPlots(modelo)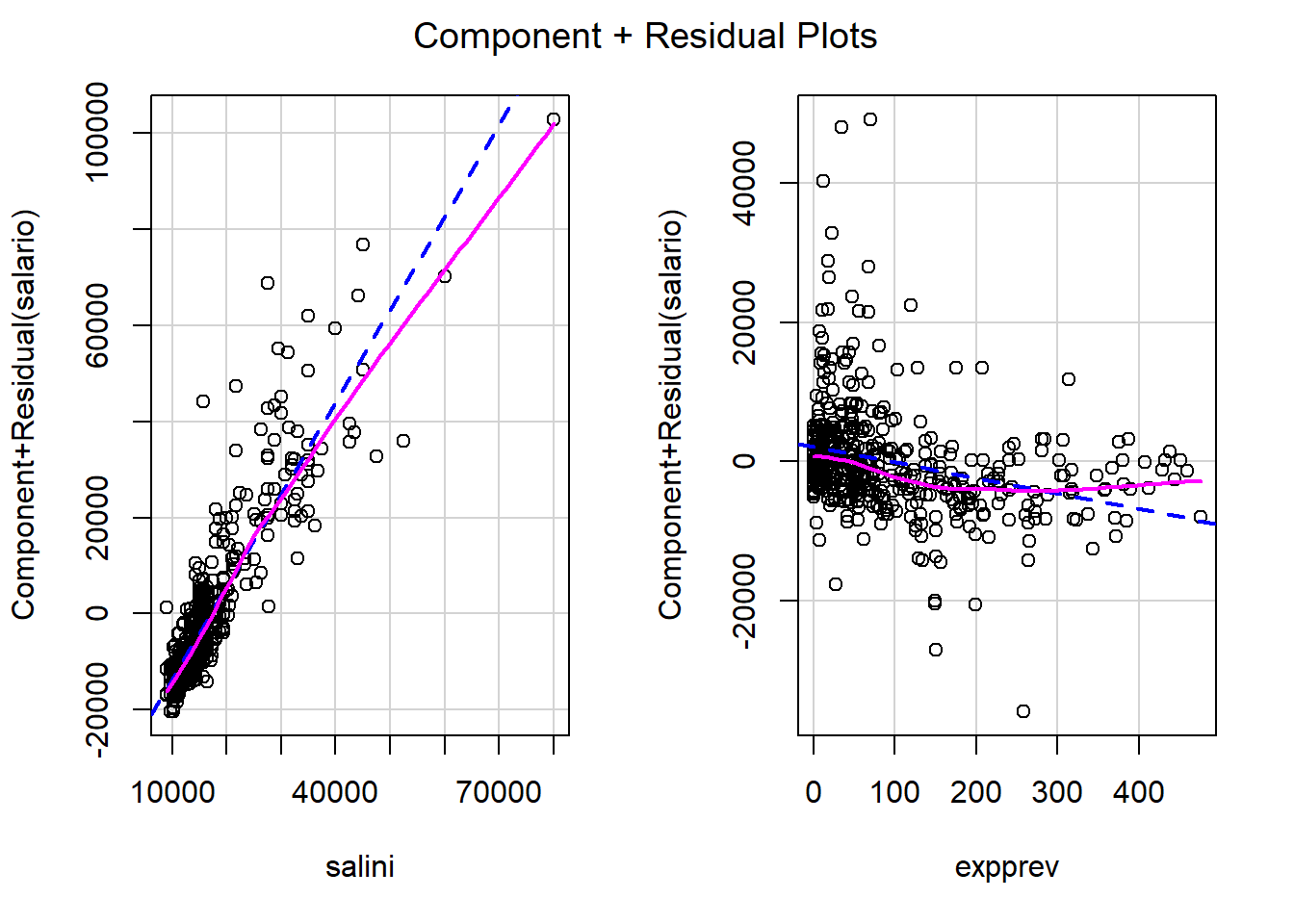
# avPlots(modelo)Estas funciones permitirían además detectar puntos atípicos o influyentes
(mediante los argumentos id.method e id.n).
8.7.3 Estadísticos
Para obtener medidas de diagnosis o resúmenes numéricos de interés se pueden emplear las siguientes funciones:
| Función | Descripción |
|---|---|
| rstandard | residuos estandarizados |
| rstudent | residuos estudentizados (eliminados) |
| cooks.distance | valores del estadístico de Cook |
| influence | valores de influencia, cambios en coeficientes y varianza residual al eliminar cada dato. |
Ejecutar help(influence.measures) para ver un listado de medidas de diagnóstico adicionales.
Hay muchas herramientas adicionales disponibles en otros paquetes.
Por ejemplo, para la detección de multicolinealidad, se puede emplear la función
vif del paquete car para calcular los factores de inflación de varianza para
las variables del modelo:
# library(car)
vif(modelo)## salini expprev
## 1.002041 1.002041Valores grandes, por ejemplo > 10, indican la posible presencia de multicolinealidad.
Nota: Las tolerancias (proporciones de variabilidad no explicada por las demás covariables) se pueden calcular con 1/vif(modelo).
8.7.4 Contrastes
8.7.4.1 Normalidad
Para realizar el contraste de normalidad de Shapiro-Wilk se puede emplear:
shapiro.test(residuals(modelo))##
## Shapiro-Wilk normality test
##
## data: residuals(modelo)
## W = 0.85533, p-value < 2.2e-16hist(residuals(modelo))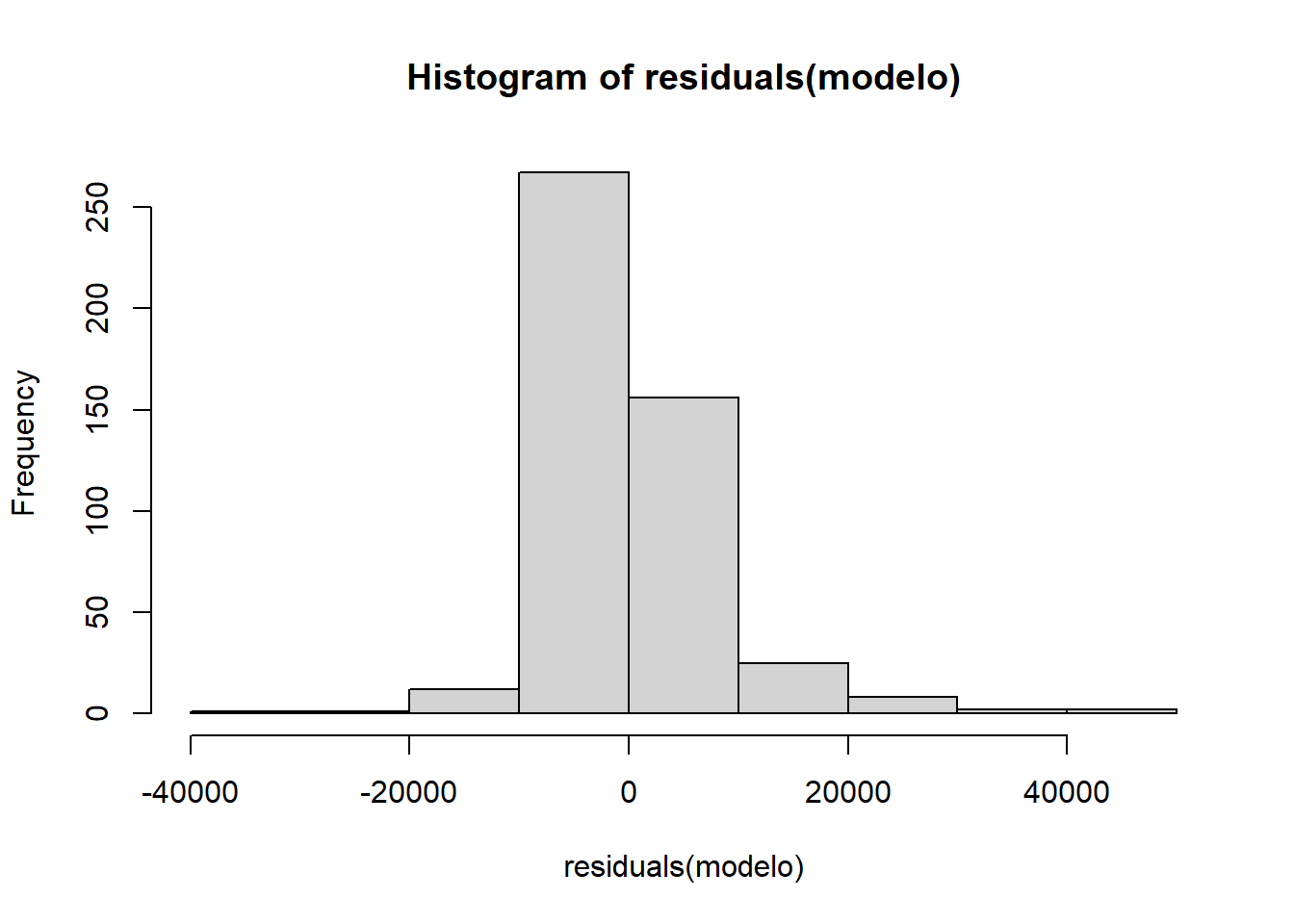
8.7.4.2 Homocedasticidad
La librería lmtest proporciona herramientas adicionales para la diagnosis de modelos lineales, por ejemplo el test de Breusch-Pagan para heterocedasticidad:
library(lmtest)
bptest(modelo, studentize = FALSE)##
## Breusch-Pagan test
##
## data: modelo
## BP = 290.37, df = 2, p-value < 2.2e-16Si el p-valor es grande aceptaríamos que hay igualdad de varianzas.
8.7.4.3 Autocorrelación
Contraste de Durbin-Watson para detectar si hay correlación serial entre los errores:
dwtest(modelo, alternative= "two.sided")##
## Durbin-Watson test
##
## data: modelo
## DW = 1.8331, p-value = 0.06702
## alternative hypothesis: true autocorrelation is not 0Si el p-valor es pequeño rechazaríamos la hipótesis de independencia.