11.1 Funciones

El lenguaje R permite al usuario definir sus propias funciones. El esquema de una función es el que sigue:

nombre <- function(arg1, arg2, ... ) {expresión}

En la expresión anterior arg1, arg2, ... son los argumentos de entrada (también llamados parámetros).
La expresión está compuesta de comandos que utilizan los argumentos de entrada para dar la salida deseada.
La salida de una función puese ser un número, un vector, una grafica, un mensaje, etc.

11.1.1 Ejemplo: progresión geométrica

Para introducirnos en las funciones, vamos a escribir una función que permita trabajar con las llamadas progresiones geométricas.

Una progresión geométrica es una sucesión de números \(a_1, a_2, a_3\ldots\) tales que cada uno de ellos (salvo el primero) es igual al anterior multiplicado por una constante llamada razón, que representaremos por \(r\). Ejemplos:

\(a_1=1\), \(r=2\):

1, 2, 4, 8, 16,…
\(a_1=-1\), \(r=-2\):

1, -2, 4, -8, 16,…

Según la definición anterior, se verifica que: \[a_2=a_1\cdot r; \quad a_3=a_2\cdot r=a_1\cdot r^2; \quad ...\] y generalizando este proceso se obtiene el llamado término general:

\[a_n=a_1\cdot r^{n-1}\]

También se puede comprobar que la suma de los \(n\) términos de la progresión es:

\[S_n=a_1+\ldots_+a_n=\frac{a_1(r^n-1)}{r-1}\]

La siguiente función, que llamaremos an calcula el término \(a_n\) de una progresión geométrica pasando como entrada el primer elemento a1, la razón r y el valor n:

an <- function(a1, r, n) {
        a1 * r^(n - 1)
      }

A continuación algún ejemplo para comprobar su funcionamiento:

an(a1 = 1, r = 2, n = 5)

## [1] 16

an(a1 = 4, r = -2, n = 6)

## [1] -128

an(a1 = -50, r = 4, n = 6)

## [1] -51200

Con la función anterior se pueden obtener, con una sola llamada, varios valores de la progresión:

an(a1 = 1, r = 2, n = 1:5)    # a1, ..., a5

## [1]  1  2  4  8 16

an(a1 = 1, r = 2, n = 10:15)  # a10, ..., a15

## [1]   512  1024  2048  4096  8192 16384

La función Sn calcula la suma de los primeros n elementos de la progresión:

Sn <- function(a1, r, n) {
        a1 * (r^n - 1) / (r - 1)
      }
  
Sn(a1 = 1, r = 2, n = 5)

## [1] 31

an(a1 = 1, r = 2, n = 1:5)    # Valores de la progresión

## [1]  1  2  4  8 16

Sn(a1 = 1, r = 2, n = 1:5)    # Suma de los valores

## [1]  1  3  7 15 31

# cumsum(an(a1 = 1, r = 2, n = 1:5))

11.1.2 Argumentos de entrada

Como ya hemos comentado, los argumentos son los valores de entrada de una función.

Por ejemplo, en la función anterior:
```
an <- function(a1, r, n) {a1 * r^(n - 1)}
```
los argumentos de entrada son a1, r y n.

Veamos alguna consideración sobre los argumentos:

No es necesario utilizar el nombre de los argumentos. En este caso es obligatorio mantener el orden de entrada. Por ejemplo, las siguientes llamadas son equivalentes:
```
an(1, 2, 5)
```
```
## [1] 16
```
```
an(a1 = 1, r = 2, n = 5)
```
```
## [1] 16
```

Si se nombran los argumentos, se pueden pasar en cualquier orden:

an(r = 2, n = 5, a1 = 1)

## [1] 16

an(n = 5, r = 2, a1 = 1)

## [1] 16

11.1.2.1 Argumentos por defecto

En muchas ocasiones resulta muy interesante que las funciones tengan argumentos por defecto.

Por ejemplo, si se quiere que en una función:

nombre <- function(arg1, arg2, arg3, arg4, ...) { expresión }

los argumento arg2 y arg3 tomen por defecto los valores a y b respectivamentebastaría con escribir:

nombre <- function(arg1, arg2 = a, arg3 = b, arg4, ...) { expresión }

Para comprender mejor esto considérese el siguiente ejemplo ilustrativo:

xy2 <- function(x = 2, y = 3) { x * y^2 }
xy2()

## [1] 18

xy2(x = 1, y = 4)

## [1] 16

xy2(y = 4)

## [1] 32

11.1.2.2 El argumento `...`

El argumento “...” permite pasar de manera “libre” argumentos adicionales para ser utilizados por otra “subfunción” dentro de la función principal.

Por ejemplo, en la función:

Density.Plot <- function(datos, ...) { plot(density(datos), ...) }

a partir del primer argumento, los argumentos se incluirán en ... y serán utilizados por la función plot.

data(cars)
Density.Plot(cars$speed)

Density.Plot(cars$speed, col = 'red', xlab = "velocidad", ylab = "distancia")

Los argumentos de entrada de una función se obtienen ejecutando args(funcion):

args(an)

## function (a1, r, n) 
## NULL

args(xy2)

## function (x = 2, y = 3) 
## NULL

str(args(Density.Plot))

## function (datos, ...)

Por otro lado, al escribir el nombre de una función se obtiene su contenido:

an

## function(a1, r, n) {
##         a1 * r^(n - 1)
##       }
## <bytecode: 0x000000001d0fcad0>

11.1.3 Salida

El valor que devolverá una función será:

el último objeto evaluado dentro de ella, o
lo indicado dentro de la sentencia return.

Como las funciones pueden devolver objetos de varios tipos es hatibual que la salida sea una lista.

an <- function(a1, r, n) { a1 * r^(n - 1) }
Sn <- function(a1, r, n) { a1 * (r^n - 1) / (r - 1) }
  
asn <- function(a1 = 1, r = 2, n = 5) {
  A <- an(a1, r, n)
  S <- Sn(a1, r, n)
  ii <- 1:n
  AA <- an(a1, r, ii)
  SS <- Sn(a1, r, ii)
  return(list(an = A, Sn = S, salida = data.frame(valores = AA, suma = SS)))
}

La función asn utiliza las funiones an y Sn programadas antes y devuelve como salida una lista con las siguientes componentes:

an: valor de \(a_n\)
Sn: valor de \(S_n\)
salida: data.frame con dos variables
- salida: vector con las \(n\) primeras componentes de la progresión
- suma: suma de las \(n\) primeras componentes

asn()

## $an
## [1] 16
## 
## $Sn
## [1] 31
## 
## $salida
##   valores suma
## 1       1    1
## 2       2    3
## 3       4    7
## 4       8   15
## 5      16   31

La salida de la función anterior es una lista y se puede acceder a los elementos de la misma:

res <- asn()
res$an

## [1] 16

res$Sn

## [1] 31

res$salida

##   valores suma
## 1       1    1
## 2       2    3
## 3       4    7
## 4       8   15
## 5      16   31

11.1.4 Otros ejemplos

11.1.4.1 Ejemplo: letra del DNI

A continuación se calculará la letra del DNI a partir de su correspondiente número. El método utilizado para obtener la letra del DNI consiste en dividir el número entre 23 y según el resto obtenido adjudicar la letra que figura en la siguiente tabla:

resto	letra	resto	letra	resto	letra
0	T	8	P	16	Q
1	R	9	D	17	V
2	W	10	X	18	H
3	A	11	B	19	L
4	G	12	N	20	C
5	M	13	J	21	K
6	Y	14	Z	22	E
7	F	15	S

La siguiente función permite obtener la letra del DNI:

DNI <- function(numero) {
  letras <- c("T", "R", "W", "A", "G", "M", "Y", "F", 
              "P", "D", "X", "B", "N", "J", "Z", "S", 
              "Q", "V", "H", "L", "C", "K", "E")
  return(letras[numero %% 23 + 1]) 
}

DNI(50247828)

## [1] "G"

11.1.4.2 Ejemplo: simulación del lanzamiento de un dado

La siguiente función simula \(n\) (por defecto \(n=100\)) lanzamientos de un dado. La función devuelve la tabla de frecuencias y realiza el correspondiente gráfico:

dado <- function(n = 100) {
  lanzamientos <- sample(1:6, n, rep = TRUE)
  frecuencias <- table(lanzamientos) / n
  barplot(frecuencias, main = paste("Número de lanzamientos=", n))
  abline(h = 1 / 6, col = 'red', lwd = 2)
  return(frecuencias)
}

A continuación se muestran los resultados obtenidos para varias simulaciones:

dado(100)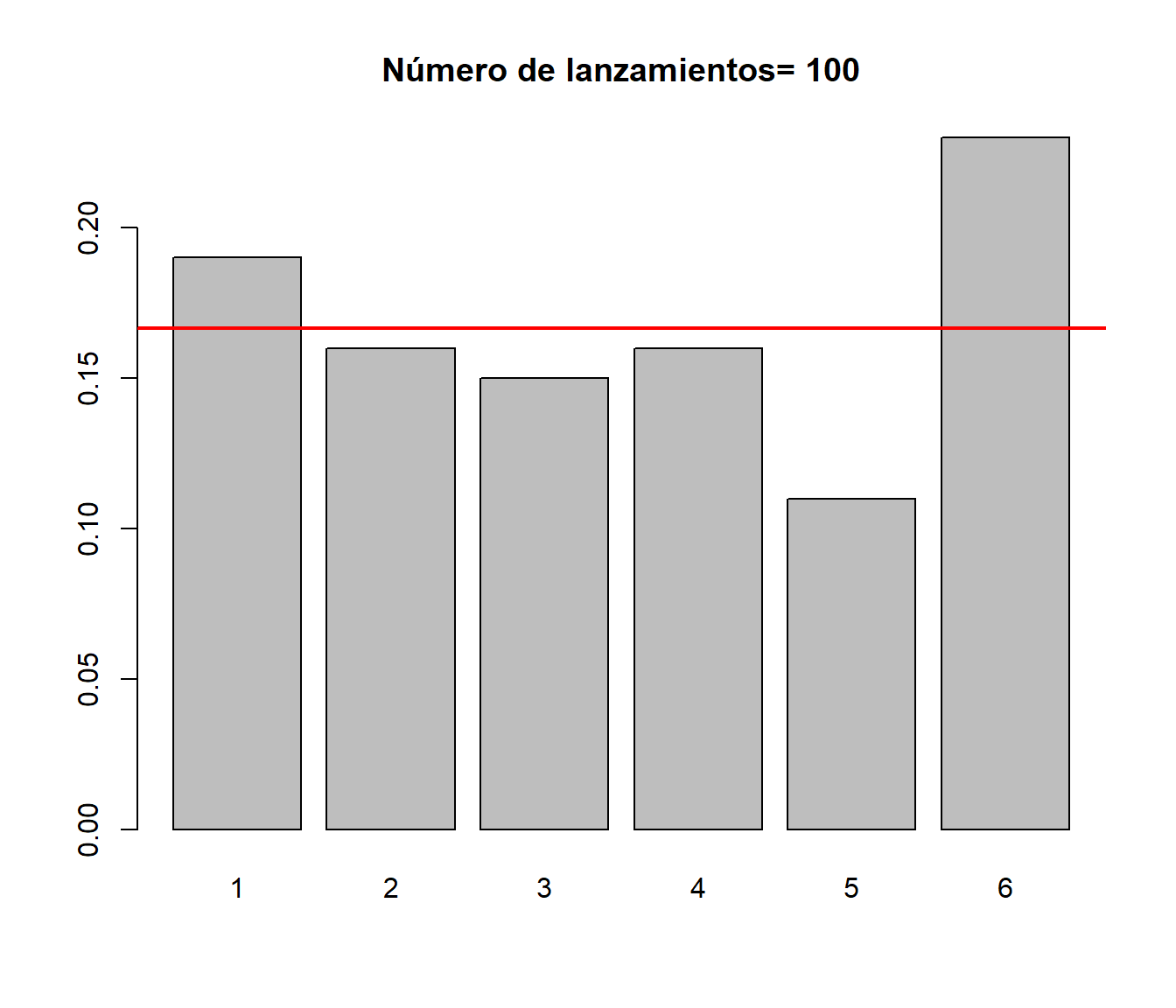

## lanzamientos
##    1    2    3    4    5    6 
## 0.19 0.16 0.15 0.16 0.11 0.23

dado(500)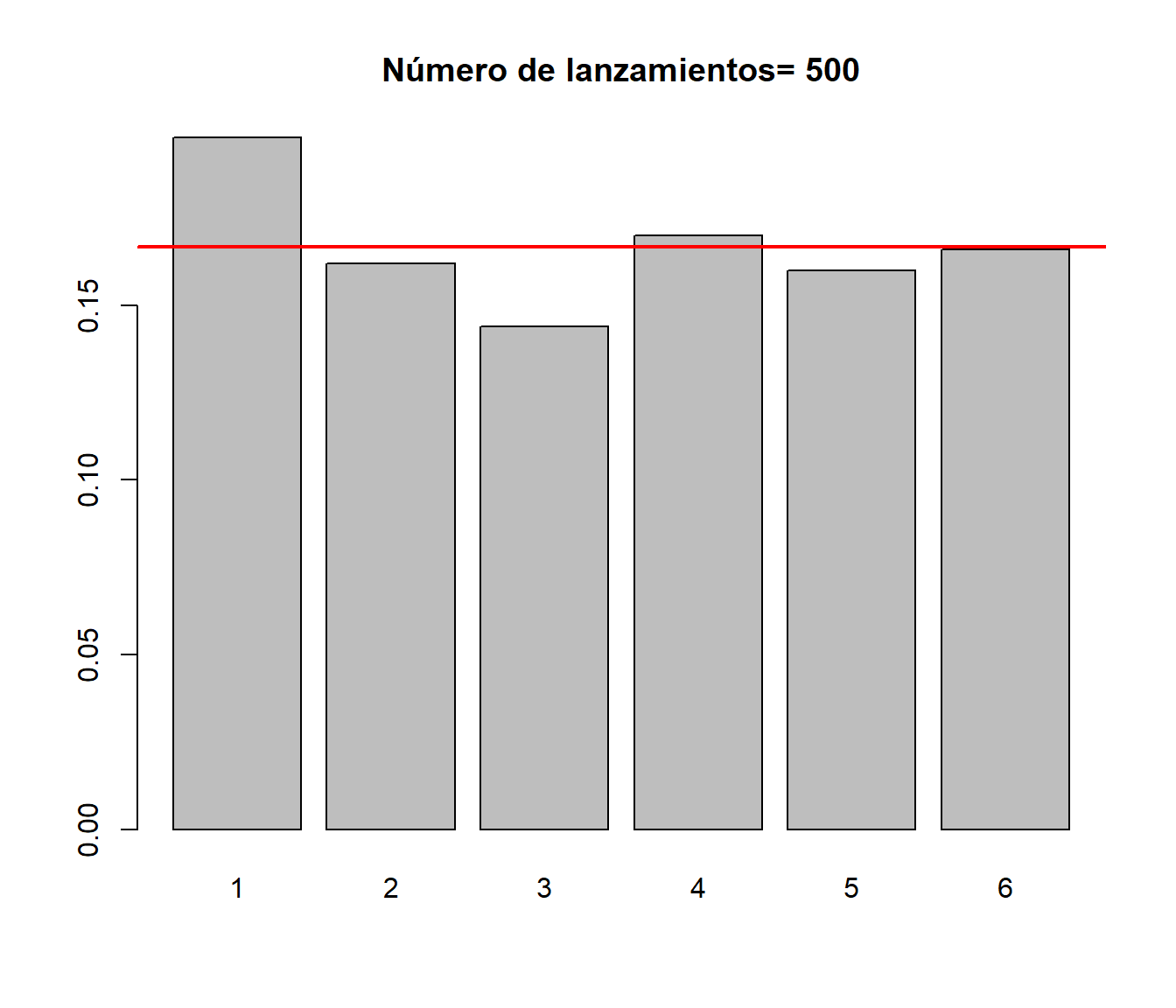

## lanzamientos
##     1     2     3     4     5     6 
## 0.198 0.162 0.144 0.170 0.160 0.166

dado(10000)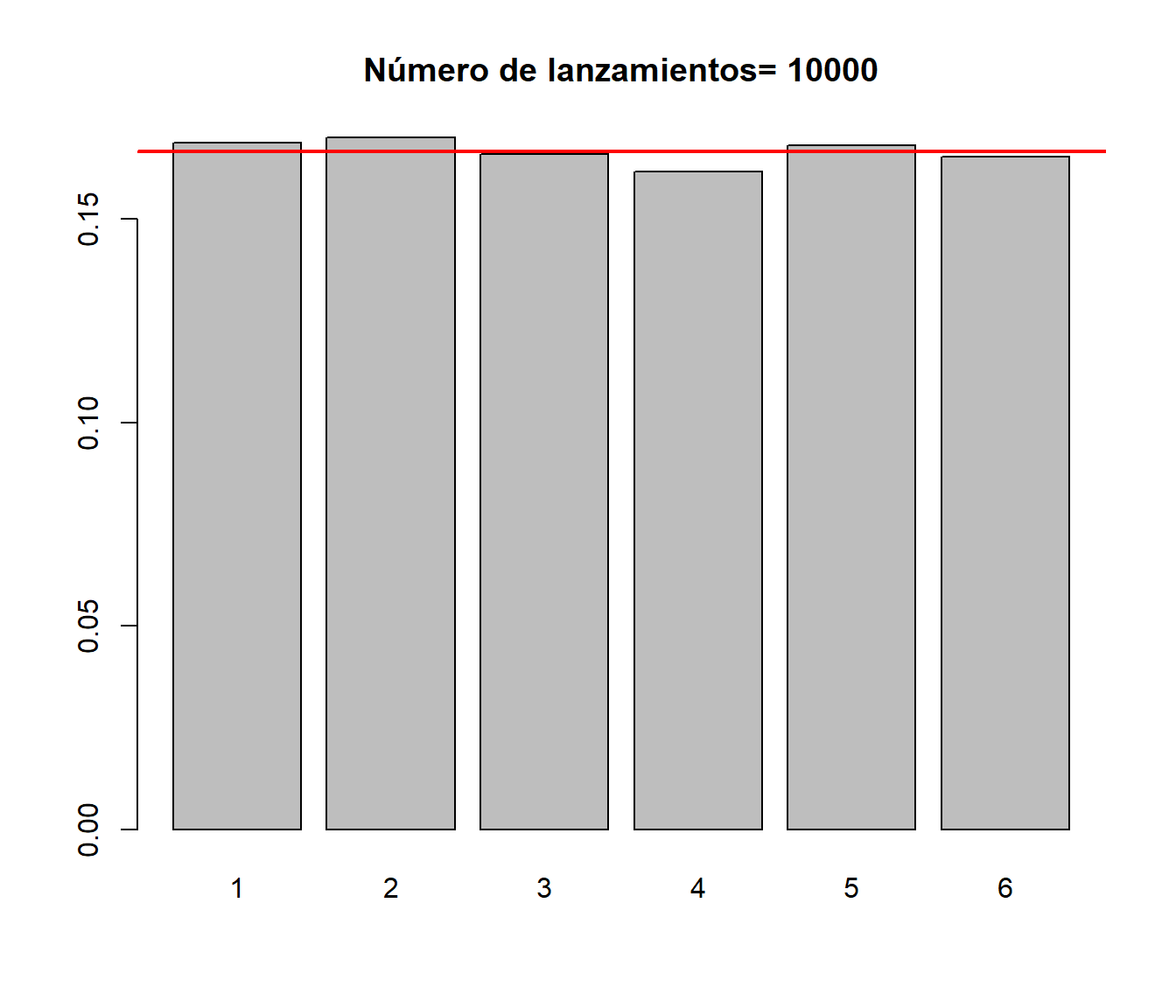

## lanzamientos
##      1      2      3      4      5      6 
## 0.1687 0.1701 0.1660 0.1616 0.1682 0.1654

Se puede comprobar que al aumentar el valor de \(n\) las frecuencias se aproximan al valor teórico \(1/6=0.1667\).

11.1.5 Variables locales y globales

En R no es necesario declarar las variables usadas dentro de una función. Se utiliza la regla llamada “ámbito lexicográfico” para decidir si un objeto es local a una función o global.

Para entender mejor esto se consideran los siguientes ejemplos:

fun <- function() print(x)
x <- 1
fun()

## [1] 1

La variable x no está definida dentro de fun, así que R busca x en el entorno en el que se llamó a la función e imprimirá su valor.

Si x es utilizado como el nombre de un objeto dentro de la función, el valor de x en el ambiente global (fuera de la función) no cambia.

x <- 1
fun2 <- function() {
    x <- 2
    print(x)
}

fun2()

## [1] 2

## [1] 1

Para que el valor “global” de una variable pueda ser cambidado dentro de una función se utiliza la doble asignación <<-.

x <- 1
y <- 3
fun2 <- function() {
    x <- 2
    y <<- 5
    print(x)
    print(y)
}

fun2()

## [1] 2
## [1] 5

x # No cambió su valor

## [1] 1

y # Cambió su valor

## [1] 5