8.8 Métodos de regularización

[[Pasar a selección de variables explicativas?]]

Estos métodos emplean también un modelo lineal: \[Y=\beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\cdots+\beta_{p}X_{p}+\varepsilon\]

En lugar de ajustarlo por mínimos cuadrados (estándar), minimizando: \[ RSS = \sum\limits_{i=1}^{n}\left( y_{i} - \beta_0 - \beta_1 x_{1i} - \cdots - \beta_p x_{pi} \right)^{2}\]

Se imponen restricciones adicionales a los parámetros que los “retraen” (shrink) hacia cero:

• Produce una reducción en la varianza de predicción (a costa del sesgo).

• En principio se consideran todas las variables explicativas.

Ridge regression

• Penalización cuadrática: \(RSS+\lambda\sum_{j=1}^{p}\beta_{j}^{2}\).

Lasso

• Penalización en valor absoluto: \(RSS+\lambda\sum_{j=1}^{p}|\beta_{j}|\).

• Normalmente asigna peso nulo a algunas variables (selección de variables).

El parámetro de penalización se selecciona por validación cruzada.

• Normalmente estandarizan las variables explicativas (coeficientes en la misma escala).

8.8.1 Datos

El fichero hatco.RData contiene observaciones de clientes de la compañía de distribución industrial (Compañía Hair, Anderson y Tatham). Las variables se pueden clasificar en tres grupos:

load('datos/hatco.RData')
as.data.frame(attr(hatco, "variable.labels"))

##          attr(hatco, "variable.labels")
## empresa                         Empresa
## tamano             Tamaño de la empresa
## adquisic      Estructura de adquisición
## tindustr              Tipo de industria
## tsitcomp    Tipo de situación de compra
## velocida           Velocidad de entrega
## precio                 Nivel de precios
## flexprec        Flexibilidad de precios
## imgfabri          Imagen del fabricante
## servconj              Servicio conjunto
## imgfvent     Imagen de fuerza de ventas
## calidadp            Calidad de producto
## fidelida   Porcentaje de compra a HATCO
## satisfac            Satisfacción global
## nfidelid        Nivel de compra a HATCO
## nsatisfa          Nivel de satisfacción

Consideraremos como respuesta la variable fidelida y como variables explicativas el resto de variables continuas menos satisfac.

library(glmnet)

El paquete glmnet no emplea formulación de modelos, hay que establecer la respuesta y y las variables explicativas x (se puede emplear la función model.matrix() para construir x, la matriz de diseño, a partir de una fórmula). En este caso, eliminamos también la última fila por tener datos faltantes:

x <- as.matrix(hatco[-100, 6:12])
y <- hatco$fidelida[-100]

8.8.2 Ridge Regression

Ajustamos un modelo de regresión ridge con la función glmnet con alpha=0 (ridge penalty).

fit.ridge <- glmnet(x, y, alpha = 0)
plot(fit.ridge, xvar = "lambda", label = TRUE)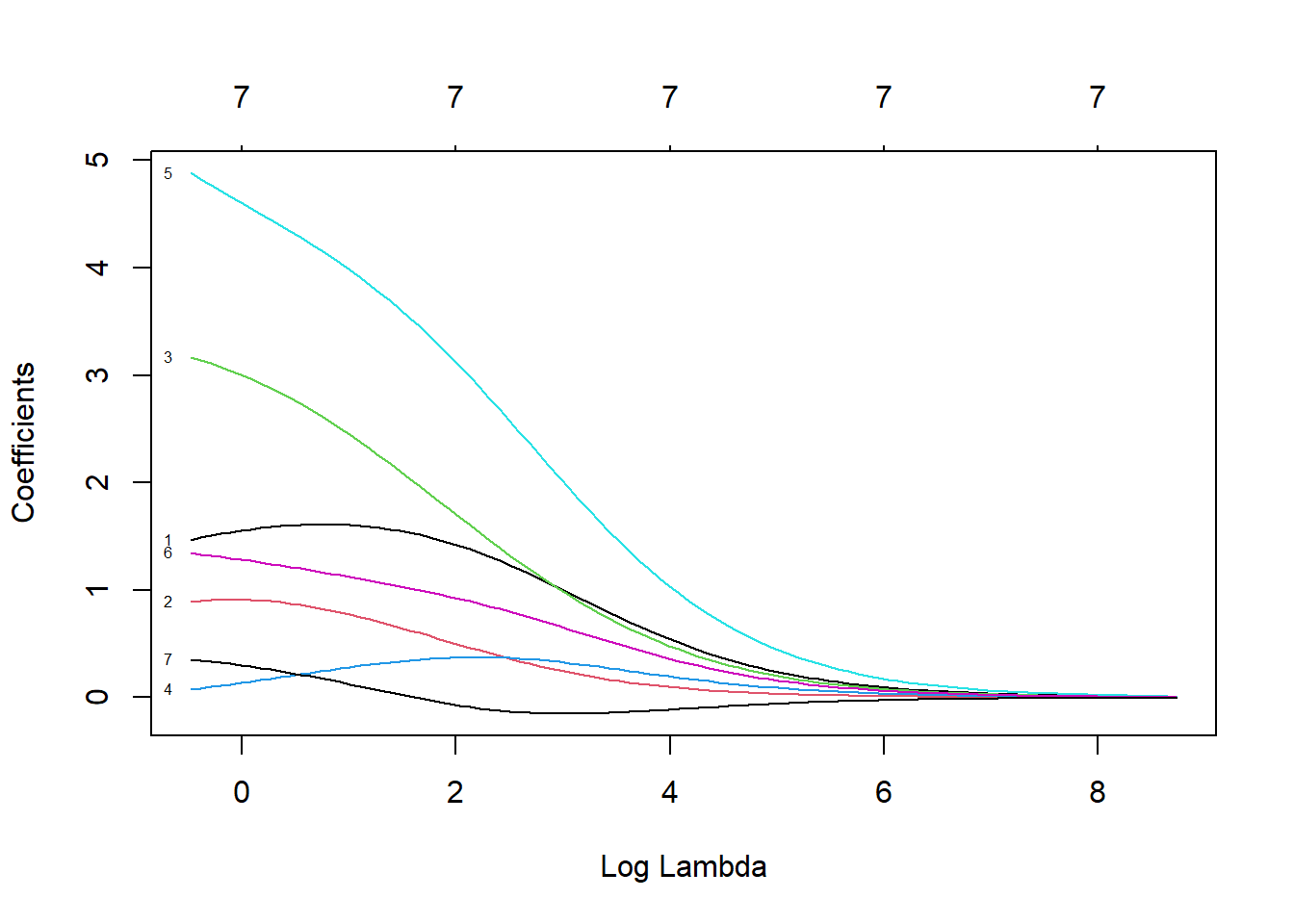

Para seleccionar el parámetro de penalización por validación cruzada se puede emplear la función cv.glmnet.

cv.ridge <- cv.glmnet(x, y, alpha = 0)
plot(cv.ridge)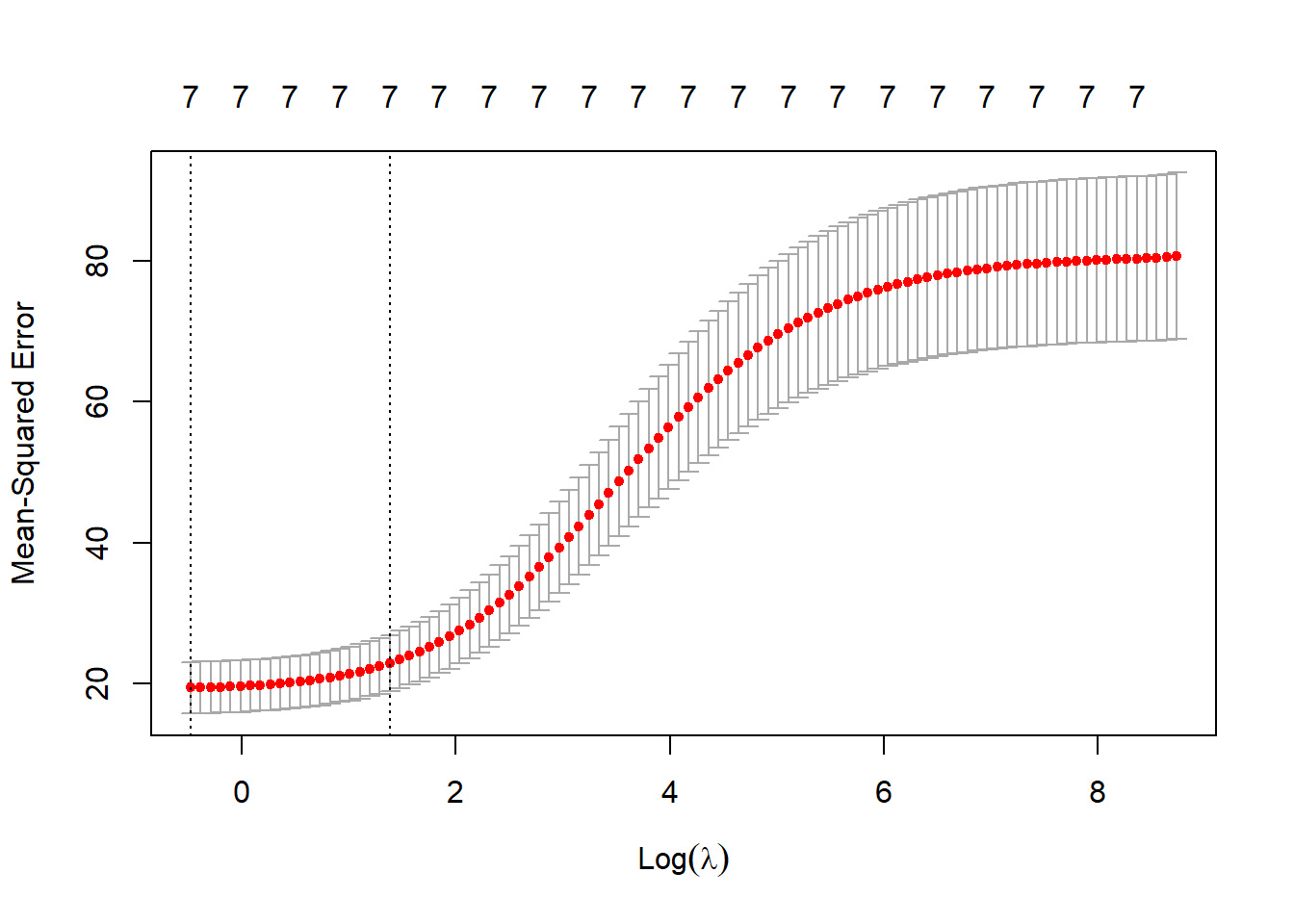

En este caso el parámetro sería:

cv.ridge$lambda.1se

## [1] 3.989587

y el modelo resultante contiene todas las variables explicativas:

coef(cv.ridge)

## 8 x 1 sparse Matrix of class "dgCMatrix"
##                     s1
## (Intercept) 6.25898621
## velocida    1.56785760
## precio      0.67897678
## flexprec    2.17894174
## imgfabri    0.32939271
## servconj    3.69427361
## imgfvent    1.05562044
## calidadp    0.04709431

8.8.3 Lasso

Ajustamos un modelo lasso también con la función glmnet (con la opción por defecto alpha=1, lasso penalty).

fit.lasso <- glmnet(x,y)
plot(fit.lasso, xvar = "lambda", label = TRUE)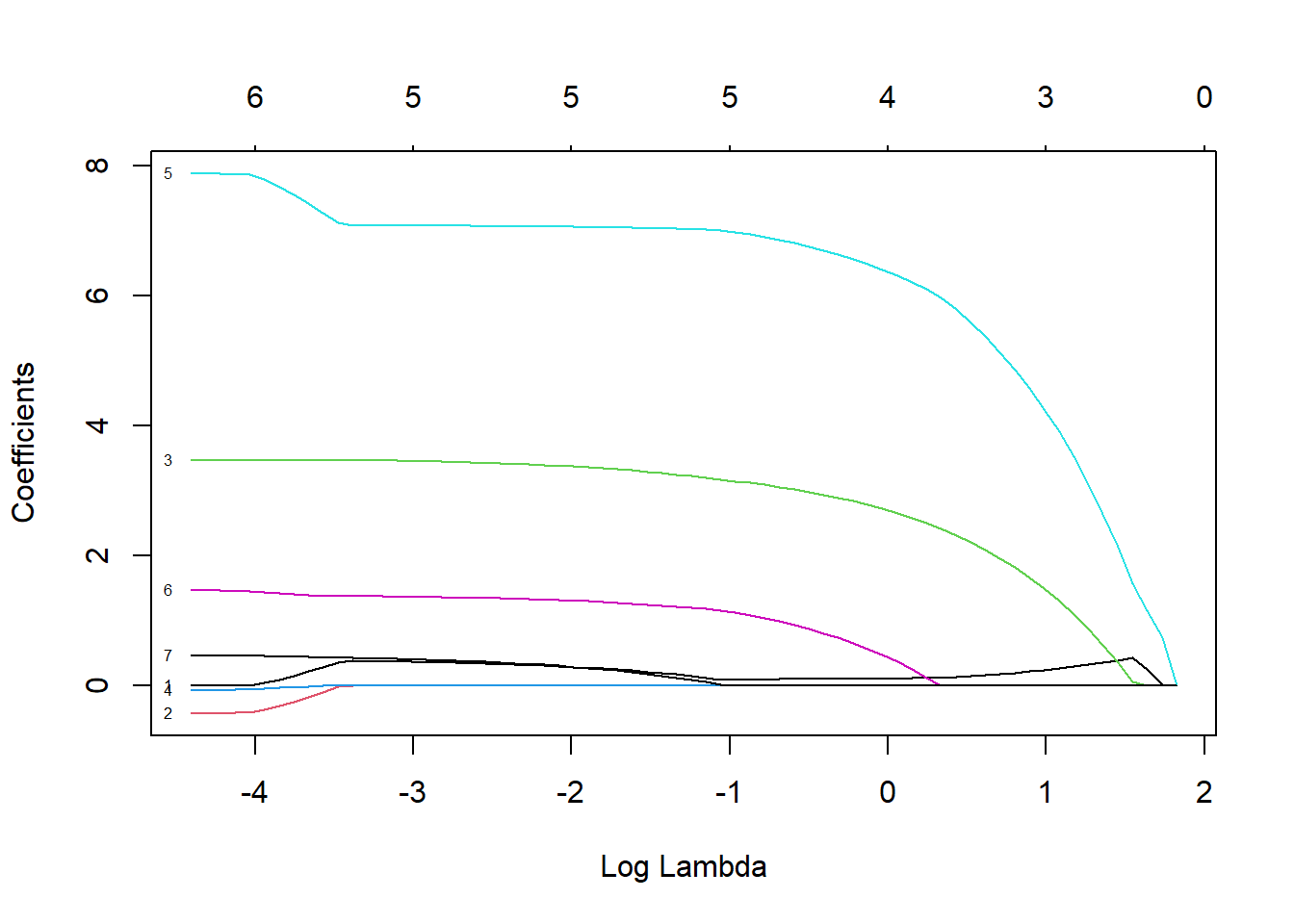

Seleccionamos el parámetro de penalización por validación cruzada.

cv.lasso <- cv.glmnet(x,y)
plot(cv.lasso)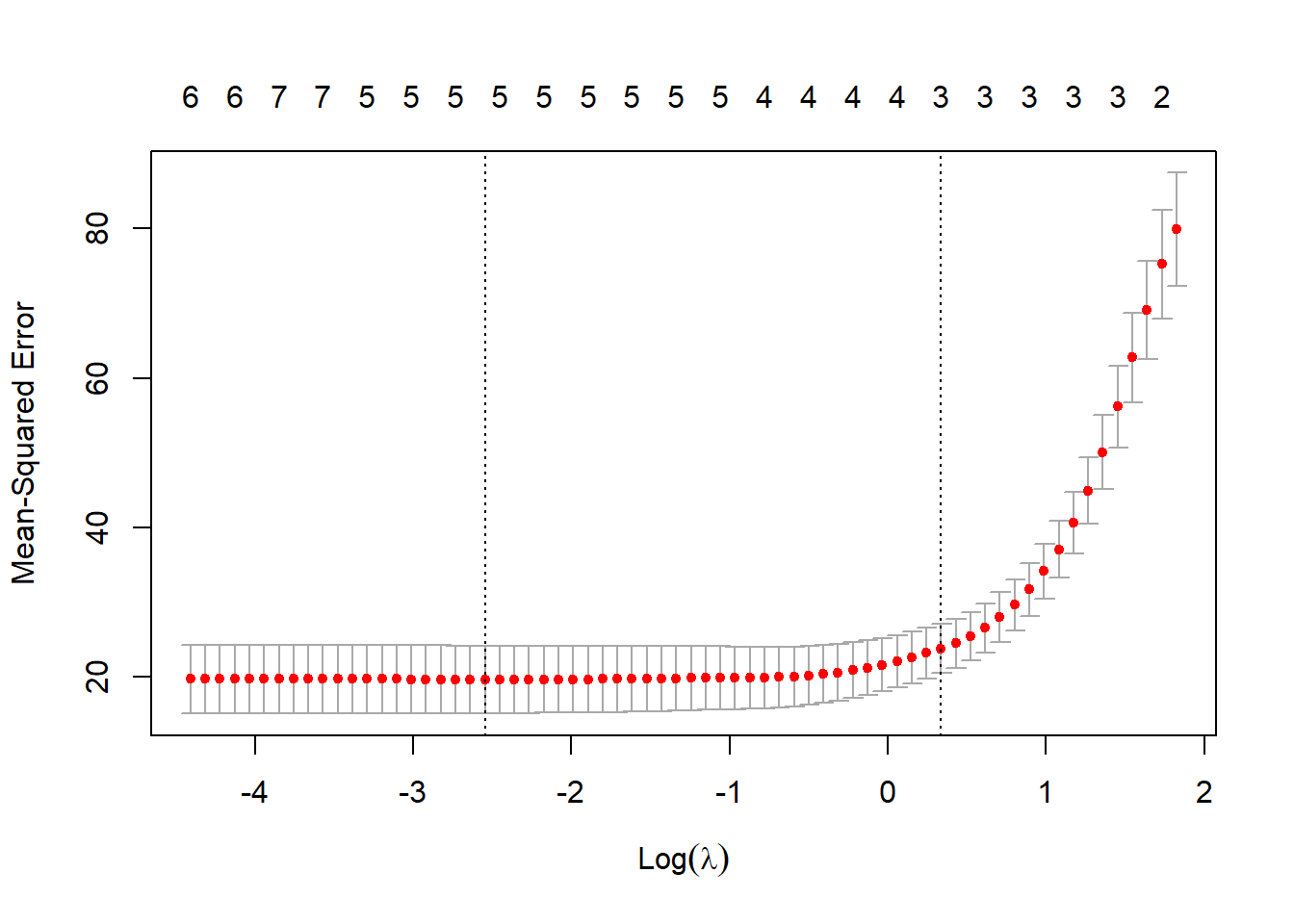

En este caso el modelo resultante solo contiene 4 variables explicativas:

coef(cv.lasso)

## 8 x 1 sparse Matrix of class "dgCMatrix"
##                    s1
## (Intercept) 9.4071399
## velocida    0.1139557
## precio      .        
## flexprec    2.4071248
## imgfabri    .        
## servconj    5.9709828
## imgfvent    .        
## calidadp    .