D.2 Análisis exploratorio

El primer paso es comenzar por un análisis exploratorio de los datos (Sección 2.5). Nos centraremos en el modelado de los datos, pero seguramente interesaría analizar si hay datos atípicos…

Estaríamos interesados en la simetría y normalidad de la respuesta (o del error). Podríamos empezar por realizar un análisis descriptivo unidimensional:

z <- aquifer_sf$head
summary(z)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   10.24   15.48   17.97   20.02   25.40   35.71

hist(z, xlab = "piezometric-head", main = "", freq = FALSE)
lines(density(z), col = 'blue')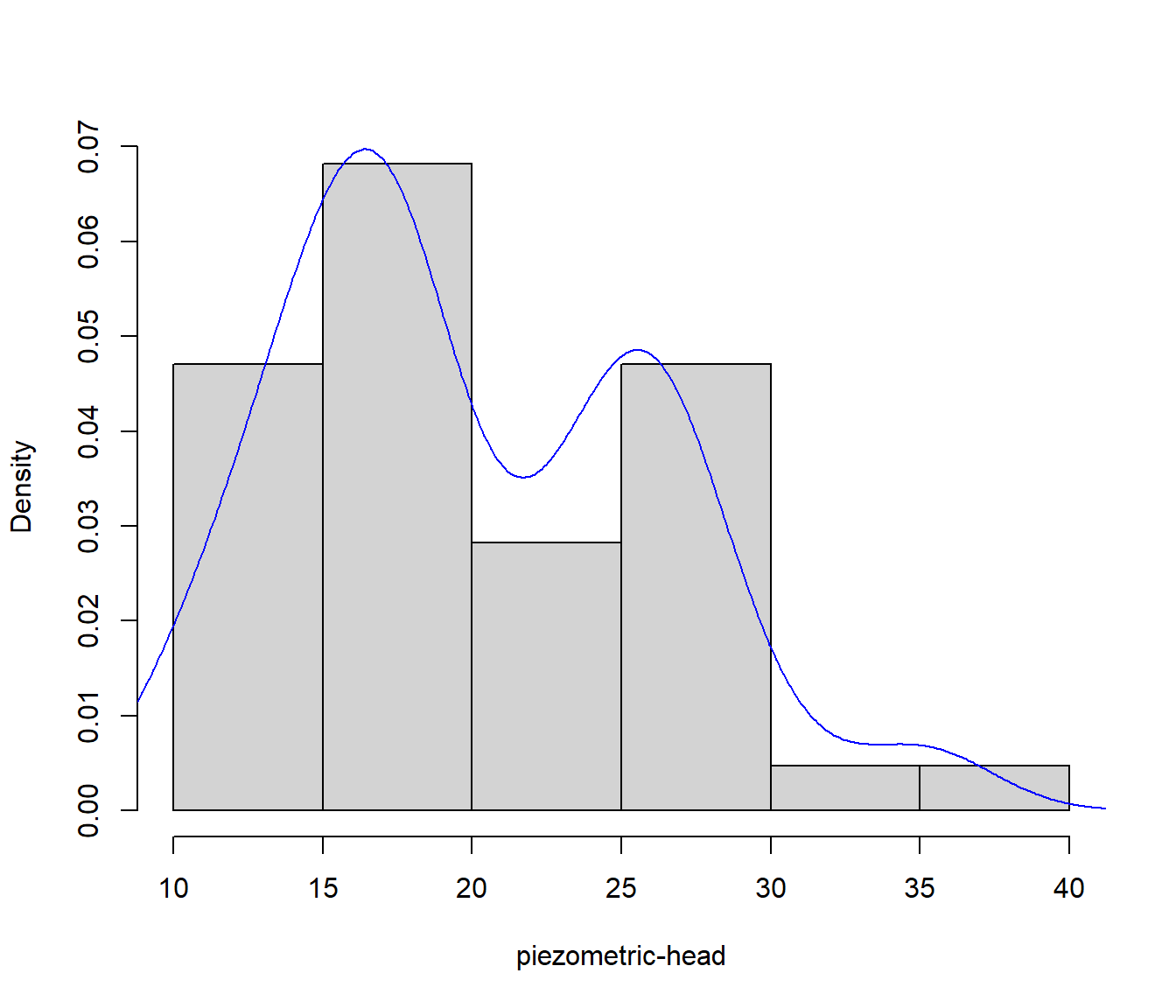

Nos interesaría estudiar si la media es constante o hay una tendencia espacial (analizar la variabilidad de gran escala). Podríamos analizar la distribución espacial de los datos:

plot(aquifer_sf["head"], pch = 20, cex = 2, breaks = "quantile", nbreaks = 4)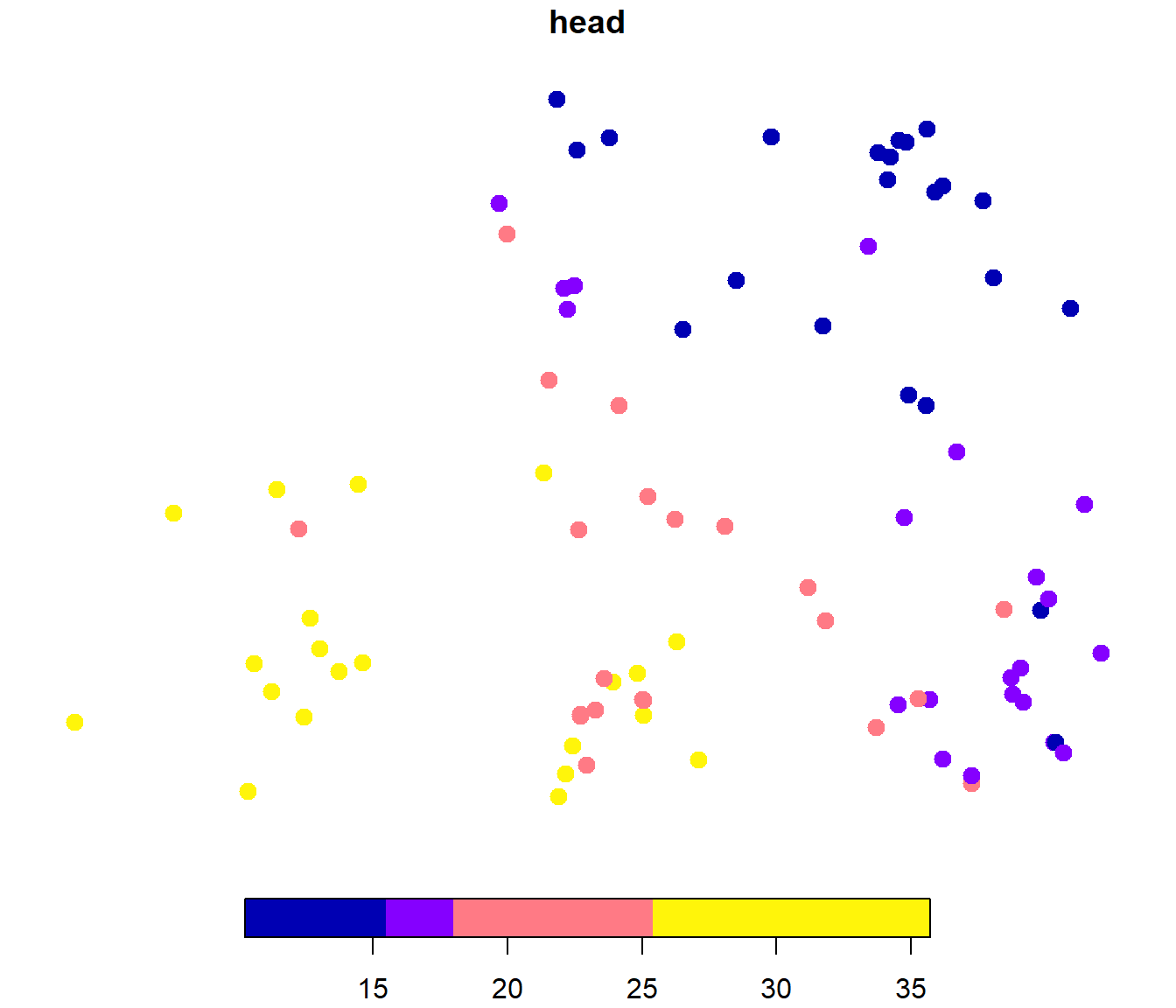

y generar gráficos de dispersión de la respuesta frente a coordenadas (o frente a otras posibles variables explicativas):

x <- aquifer_sf$lon
y <- aquifer_sf$lat
old.par <- par(mfrow = c(1, 2), omd = c(0.05, 0.95, 0.01, 0.95))
plot(x, z)
lines(lowess(x, z), lty = 2, lwd = 2, col = 'blue')
plot(y, z)
lines(lowess(y, z), lty = 2, lwd = 2, col = 'blue')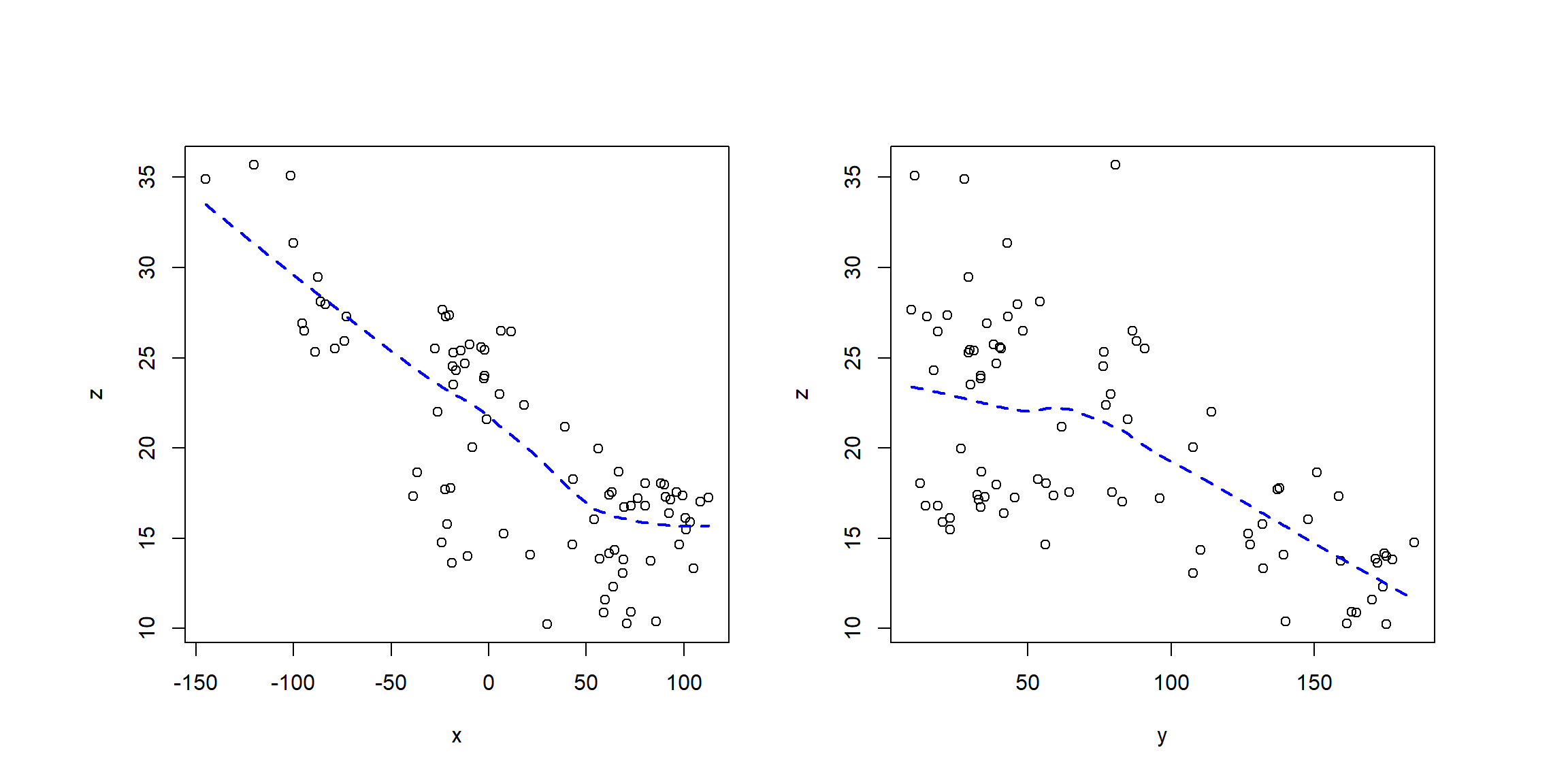

par(old.par)

Como resultado de este análisis se propondría un modelo inicial para la tendencia (incluyendo el caso de media constante, de la forma respuesta ~ 1, que se correspondería con el kriging ordinario). En este caso parece razonable considerar (como punto de partida) un modelo lineal head ~ lon + lat para la tendencia (modelo del kriging universal).

Podríamos empezar por ajustar el modelo por OLS (cuidado con los resultados de inferencia, ya que en principio no sería razonable asumir que las observaciones son independientes y por ejemplo la varianza estaría subestimada) y analizar los residuos…

trend.ols <- lm(head ~ lon + lat, data = aquifer_sf)
summary(trend.ols)

## 
## Call:
## lm(formula = head ~ lon + lat, data = aquifer_sf)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.6700 -1.6141 -0.3074  1.4823  6.5117 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 25.913266   0.389636   66.51   <2e-16 ***
## lon         -0.067519   0.003439  -19.64   <2e-16 ***
## lat         -0.059862   0.004066  -14.72   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.033 on 82 degrees of freedom
## Multiple R-squared:  0.892,  Adjusted R-squared:  0.8894 
## F-statistic: 338.8 on 2 and 82 DF,  p-value: < 2.2e-16

z <- residuals(trend.ols)
summary(z)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
## -3.6700 -1.6141 -0.3074  0.0000  1.4823  6.5117

hist(z, xlab = "ols residuals", main = "", freq = FALSE)
lines(density(z), col = 'blue')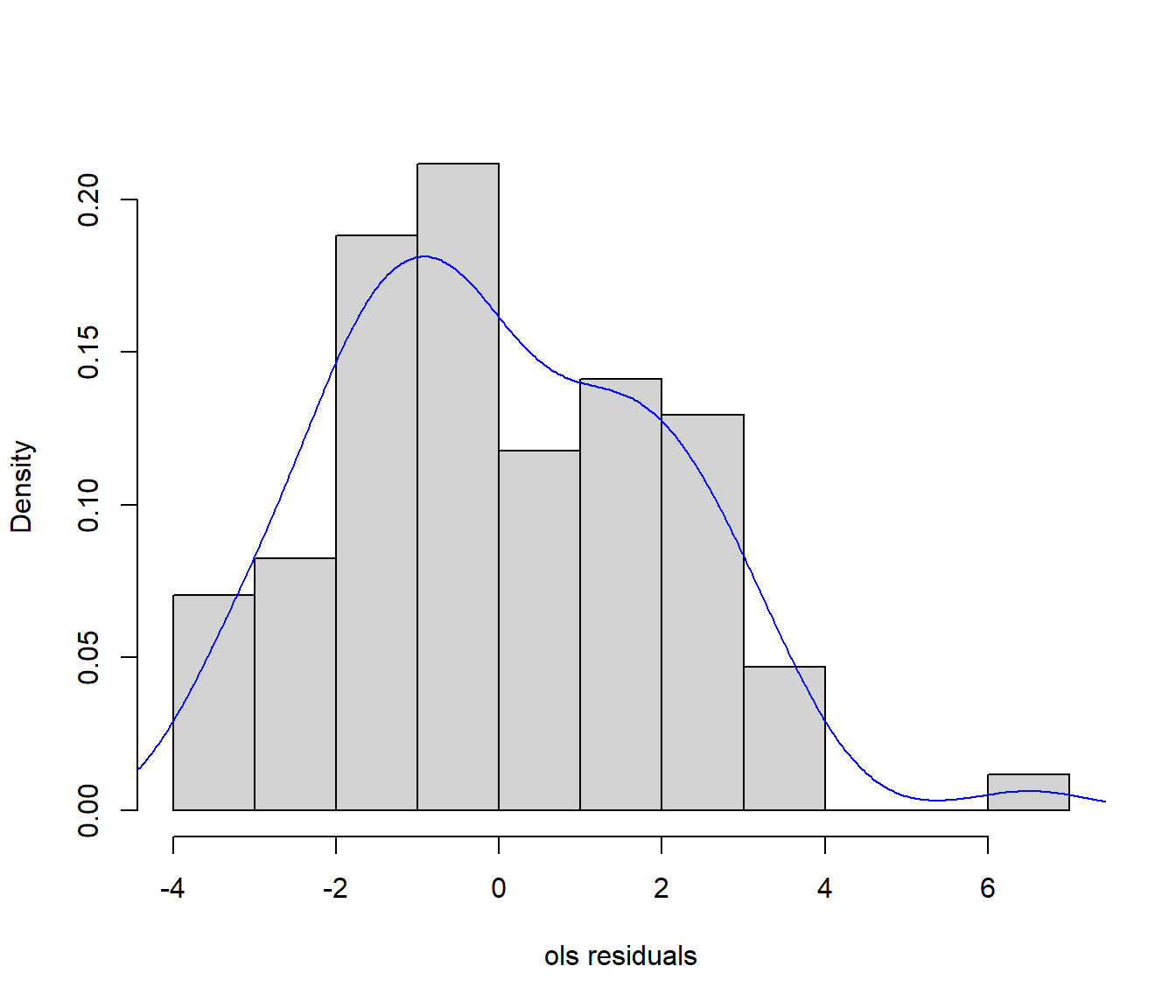

El análisis de la variabilidad de pequeña escala se realizaría a través de las semivarianzas (clásicas o robustas, Sección 3.1), pero solo consideraremos los estimadores muestrales, para el modelado de la dependencia espacial.