1.1 Procesos espaciales
Supongamos que \(Z(\mathbf{s})\) es un valor aleatorio en la posición espacial \(\mathbf{s} \in \mathbb{R}^{d}\). Entonces, si \(\mathbf{s}\) varía dentro del conjunto índice \(D\subset \mathbb{R}^{d}\) se obtiene el proceso espacial: \[\left\{ Z(\mathbf{s}) : \mathbf{s} \in D \subset \mathbb{R}^{d} \right\}\] (también se suele denominar función aleatoria, campo espacial aleatorio o variable regionalizada). Una realización del proceso espacial se denotará por \(\left\{ z(\mathbf{s}) : \mathbf{s} \in D \right\}\), pero normalmente solo se observará \(\{z(\mathbf{s}_1), z(\mathbf{s}_2), \ldots, z(\mathbf{s}_n)\}\), una realización parcial en \(n\) posiciones espaciales.
Se suele distinguir entre distintos tipos de procesos espaciales dependiendo de las suposiciones acerca del dominio \(D\):
Procesos geoestadísticos (índice espacial continuo): \(D\) es un subconjunto fijo que contiene un rectángulo \(d\)-dimensional de volumen positivo. El proceso puede ser observado de forma continua dentro del dominio. Un ejemplo claro sería la temperatura, aunque normalmente solo se dispone de datos en estaciones meteorológicas fijas, se podría observar en cualquier posición (y por tanto tiene sentido predecirla).
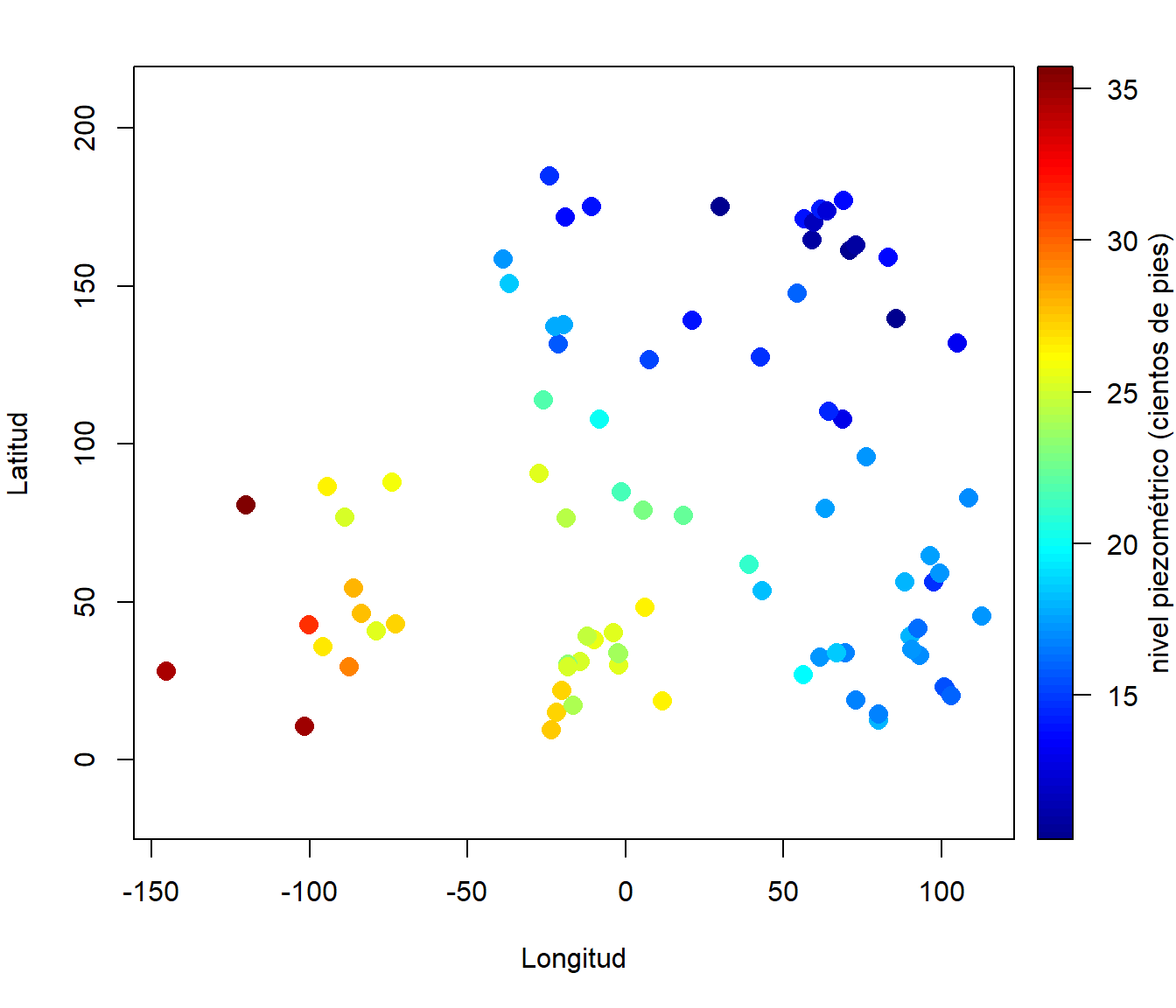
Figura 1.1: Nivel del agua subterránea en 85 localizaciones del acuífero Wolfcamp (obtenidas durante un estudio sobre el posible emplazamiento de un depósito de residuos nucleares).
Procesos reticulares/regionales (índice espacial discreto): \(D\) es un conjunto numerable de posiciones o regiones. El proceso solo puede ser observado en determinadas posiciones. Es habitual que los datos se correspondan con agregaciones (totales o valores medios) de una determinada zona (por ejemplo, países, provincias, ayuntamientos, zonas sanitarias…). Son muy comunes en econometría o epidemiología.
).](01-introduccion_files/figure-html/mortalidad-1.png)
Figura 1.2: Porcentaje de incremento de las defunciones en el año 2020 respecto al 2019 por CCAA (datos INE).
Procesos/patrones puntuales (índice espacial aleatorio): \(D\) es un proceso puntual en \(\mathbb{R}^{d}\). Las posiciones en las que se observa el proceso son aleatorias. En muchas casos interesa únicamente la posición donde se observa el evento de interés (por ejemplo la posición en la que creció un árbol de una determinada especie). En el caso general, además de la posición se podría observar alguna otra característica (una marca; por ejemplo la altura o el diámetro del árbol), es lo que se conoce como proceso puntual marcado. Este tipo de datos son habituales en biología, ecología, criminología, etc.
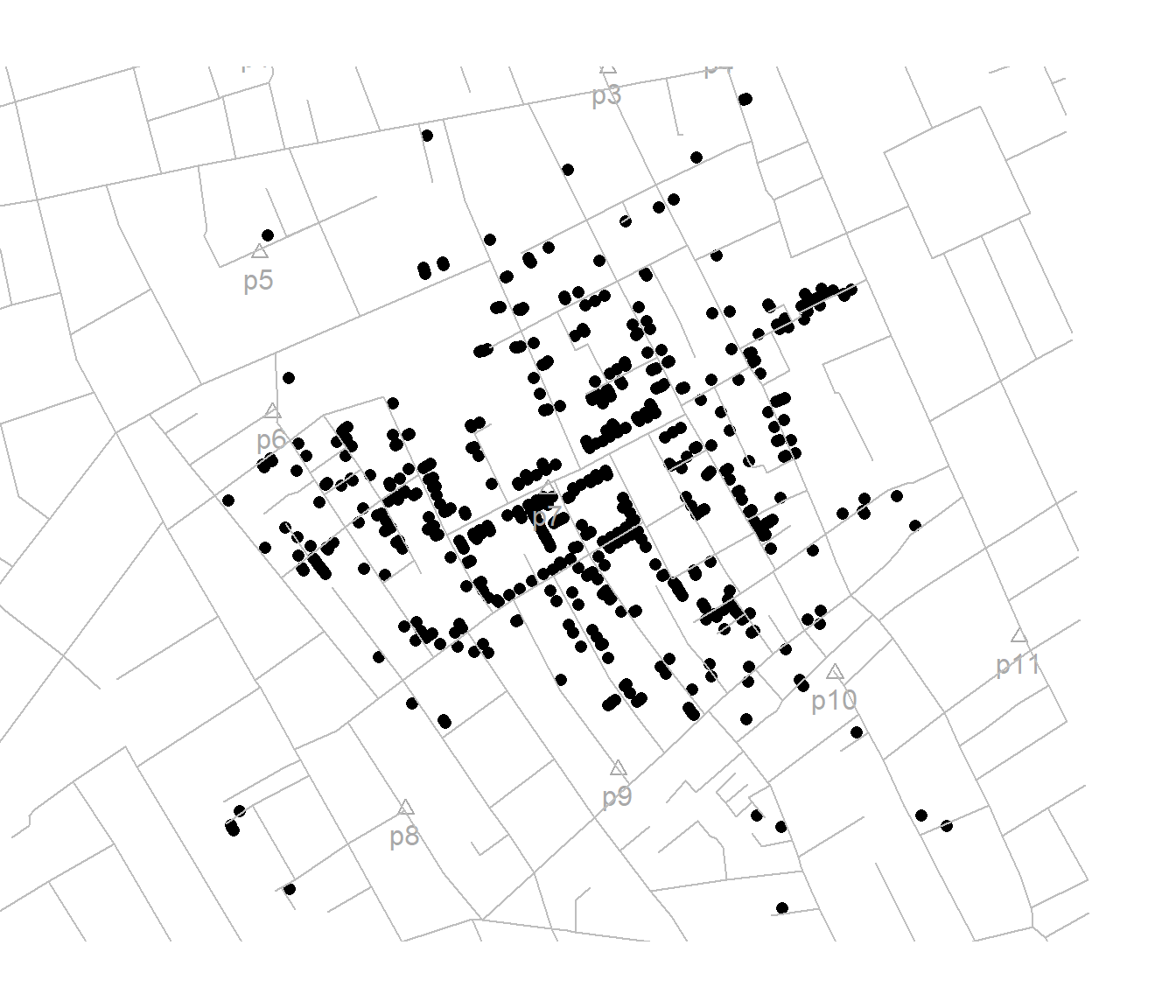
Figura 1.3: Mapa (de John Snow) del brote de cólera de 1854 en Londres.
Nos centraremos en el caso de procesos geoestadísticos (también denominados procesos espaciales continuos). El caso de posiciones espaciales discretas se considerará como resultado de la discretización de un proceso continuo. Esto sería válido también para el caso espacio-temporal, por ejemplo podríamos considerar posiciones de la forma \(\mathbf{s}=(s_{1} , \ldots,s_{d-1} ,t) \in \mathbb{R}^{d-1} \times \mathbb{R}^{+,0}\), donde \(\mathbb{R}^{+,0} = \left\{ t \in \mathbb{R} : t \geq 0 \right\}\). Por tanto, las definiciones y métodos para procesos espaciales son en principio aplicables también al caso espacio-temporal. Sin embargo, la componente temporal presenta diferencias respecto a la componente espacial…
1.1.1 Paquetes de R
En R hay disponibles una gran cantidad de paquetes para el análisis estadístico de datos espaciales (ver por ejemplo CRAN Task View: Analysis of Spatial Data). Entre ellos podríamos destacar:
Procesos geoestadísticos:
gstat,geoR,geoRglm,fields,spBayes,RandomFields,VR:spatial,sgeostat,vardiag,npsp…Procesos reticulares/regionales:
spdep,DCluster,spgwr,ade4…Procesos puntuales:
spatstat,VR:spatial,splancs…
Algunos de estos paquetes son la referencia para el análisis de este tipo de datos,
aunque también están disponibles otros, como por ejemplo maptools, geosphere, tmap, mapsf, leaflet, mapview, mapdeck, ggmap, rgrass7, RSAGA, RPyGeo, RQGIS o r-arcgis, que implementan herramientas adicionales y permiten, por ejemplo, generar gráficos interactivos o interactuar con sistemas externos de información geográfica (GIS).
En todos estos paquetes se trabajan con similares tipos de datos (espaciales y espacio-temporales) por lo que se han desarrollado paquetes que facilitan su manejo.
Entre ellos destacan el paquete sp Bivand et al. (2013) y el paquete sf E. Pebesma y Bivand (2021).
Otros paquetes para la manipulación de datos que pueden ser de interés son: raster, terra, starts, rgdal y rgeos, entre otros.
En la Sección 2.1 se incluye información adicional sobre estos paquetes.
En este libro emplearemos principalmente el paquete gstat para el análisis de datos geoestadísticos (siguiente sección; aunque se incluye una introducción al paquete geoR en el Apéndice B) y el paquete sf para la manipulación de datos espaciales (en el Apéndice A se incluye una breve introducción a las clases sp para datos espaciales).
1.1.2 El paquete gstat
El paquete gstat permite la modelización geoestadística (univariante, Capítulo 3, y multivariante, Capítulo 5), espacial y espacio-temporal (Capítulo 6), incluyendo predicción y simulación (Capítulo 4 y secciones 5.X y 6.X).
library(gstat)Este paquete implementa su propia estructura de datos (S3, basada en data.frame) pero también es compatible con los objetos Spatial* del paquete sp (Apéndice A) y los objetos de datos de los paquetes sf y stars (Capítulo 2).
Para más información se pueden consultar la referencia, las viñetas del paquete:
- The meuse data set: a tutorial for the gstat R package,
- Spatio-Temporal Geostatistics using gstat,
- Introduction to Spatio-Temporal Variography,
el blog r-spatial o las correspondientes publicaciones (Pebesma, 2004; Gräler, Pebesma y Heuvelink, 2016).
Este paquete de R es una evolución de un programa independiente anterior con el mismo nombre (Pebesma y Wesseling, 1998; basado en la librería GSLIB, Deutsch y Journel, 1992). Puede resultar de interés consultar el manual original para información adicional sobre los detalles computacionales.