4.4 Kriging con el paquete gstat
Los métodos kriging (KS, KO y KU) están implementados en la función krige() del paquete gstat.
Normalmente la sintaxis empleada es:
krige(formula, locations, newdata, model, ..., beta)formula: fórmula que define la tendencia como un modelo lineal de la respuesta en función de las variables explicativas (para KO será de la formaz ~ 1).locations: objetosfoSpatial*que contiene las observaciones espaciales (incluyendo las variables explicativas).newdata: objetosf,starsoSpatial*, que contiene las posiciones de predicción (incluyendo las variables explicativas).model: modelo de semivariograma (generado con la funciónvgm()ofit.variogram()).beta: vector con los coeficientes de tendencia (incluida la intersección) si se supone conocida (se empleará para KS, en lugar de las estimaciones GLS empleadas en KO y KU).
Esta función, además de kriging univariante puntual con vecindario global, también implementa kriging por bloques, cokriging (predicción multivariante), predicción local y simulación condicional. Para predicción (o simulación) local se pueden establecer los siguientes parámetros adicionales (ver Sección 4.5.3):
maxdist: solo se utilizarán las observaciones a una distancia de la posición de predicción menor de este valor.nmax,nmin(opcionales): número máximo y mínimo de observaciones más cercanas. Si el número de observaciones más cercanas dentro de la distanciamaxdistes menor quenmin, se generará un valor faltante.omax(opcional): número máximo de observaciones por octante (3D) o cuadrante (2D).
Los parámetros (opcionales) para simulación condicional (ver e.g. Fernández-Casal y Cao, 2020, Sección 7.5) son:
nsim: número de generaciones. Si se establece un valor distinto de cero, se emplea simulación condicional en lugar de predicción kriging.indicators: valor lógico que determina el método de simulación. Por defecto (FALSE) emplea simulación condicional gaussiana, en caso contrario (TRUE) simula una variable indicadora.
Como ejemplo consideraremos los datos del acuífero Wolfcamp con el modelo del kriging universal ajustado en la Sección 3.3.2 (en s100 se tiene un ejemplo adicional empleando KO).
load("datos/aquifer.RData")
library(sf)
aquifer$head <- aquifer$head/100 # en cientos de pies...
aquifer_sf <- st_as_sf(aquifer, coords = c("lon", "lat"), remove = FALSE, agr = "constant")
library(gstat)
vario <- variogram(head ~ lon + lat, aquifer_sf, cutoff = 150)
fit <- fit.variogram(vario, vgm(model = "Sph", nugget = NA), fit.method = 2)Como se mostró en el Ejemplo 2.1, para generar la rejilla de predicción podemos utilizar la función st_as_stars() del paquete stars considerando un buffer de radio 40 en torno a las posiciones espaciales:
buffer <- aquifer_sf %>% st_geometry() %>% st_buffer(40)
library(stars)
grid <- buffer %>% st_as_stars(nx = 50, ny = 50)Como suponemos un modelo (no constante) para la tendencia, es necesario añadir los valores de las variables explicativas a la rejilla de predicción:
coord <- st_coordinates(grid)
grid$lon <- coord$x
grid$lat <- coord$yAdemás, en este caso recortamos la rejilla para filtrar predicciones alejadas de las observaciones:
grid <- grid %>% st_crop(buffer)Obtenemos las predicciones mediante kriging universal (Sección 4.3):
pred <- krige(formula = head ~ lon + lat, locations = aquifer_sf, model = fit,
newdata = grid)## [using universal kriging]Aparentemente hay un ERROR en krige() y cambia las coordenadas del objeto stars:
summary(st_coordinates(grid))## x y
## Min. :-181.86 Min. :-28.03
## 1st Qu.:-100.73 1st Qu.: 33.25
## Median : -16.22 Median : 97.09
## Mean : -16.22 Mean : 97.09
## 3rd Qu.: 68.29 3rd Qu.:160.93
## Max. : 149.42 Max. :222.21summary(st_coordinates(pred))## x y
## Min. :-181.86 Min. : 53.83
## 1st Qu.:-100.73 1st Qu.:115.11
## Median : -16.22 Median :178.95
## Mean : -16.22 Mean :178.95
## 3rd Qu.: 68.29 3rd Qu.:242.79
## Max. : 149.42 Max. :304.08Para evitar este problema podemos añadir los resultado al objeto grid y emplearlo en lugar de pred:
grid$var1.pred <- pred$var1.pred
grid$var1.var <- pred$var1.varPodemos representar las predicciones y las varianzas kriging empleando plot.stars():
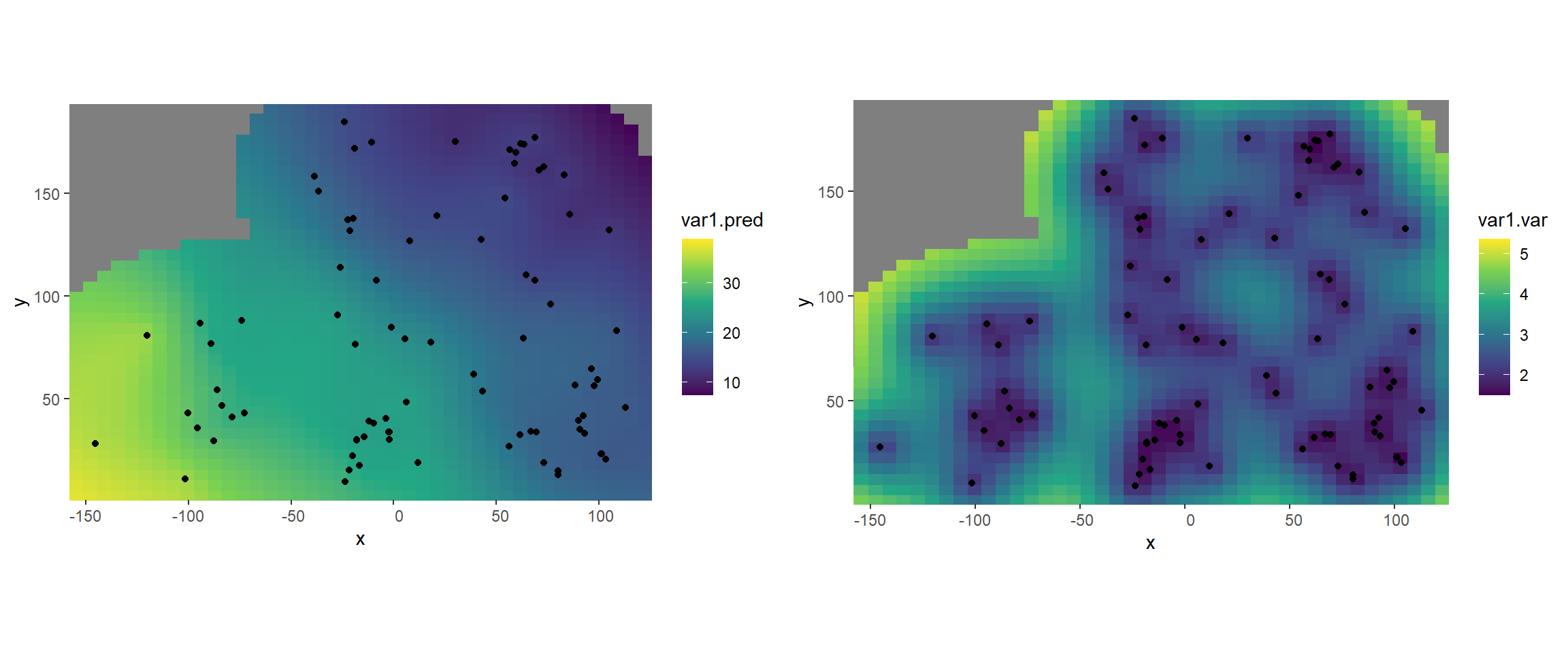
plot(grid["var1.pred"], breaks = "equal", col = sf.colors(64), key.pos = 4,
main = "Predicciones kriging")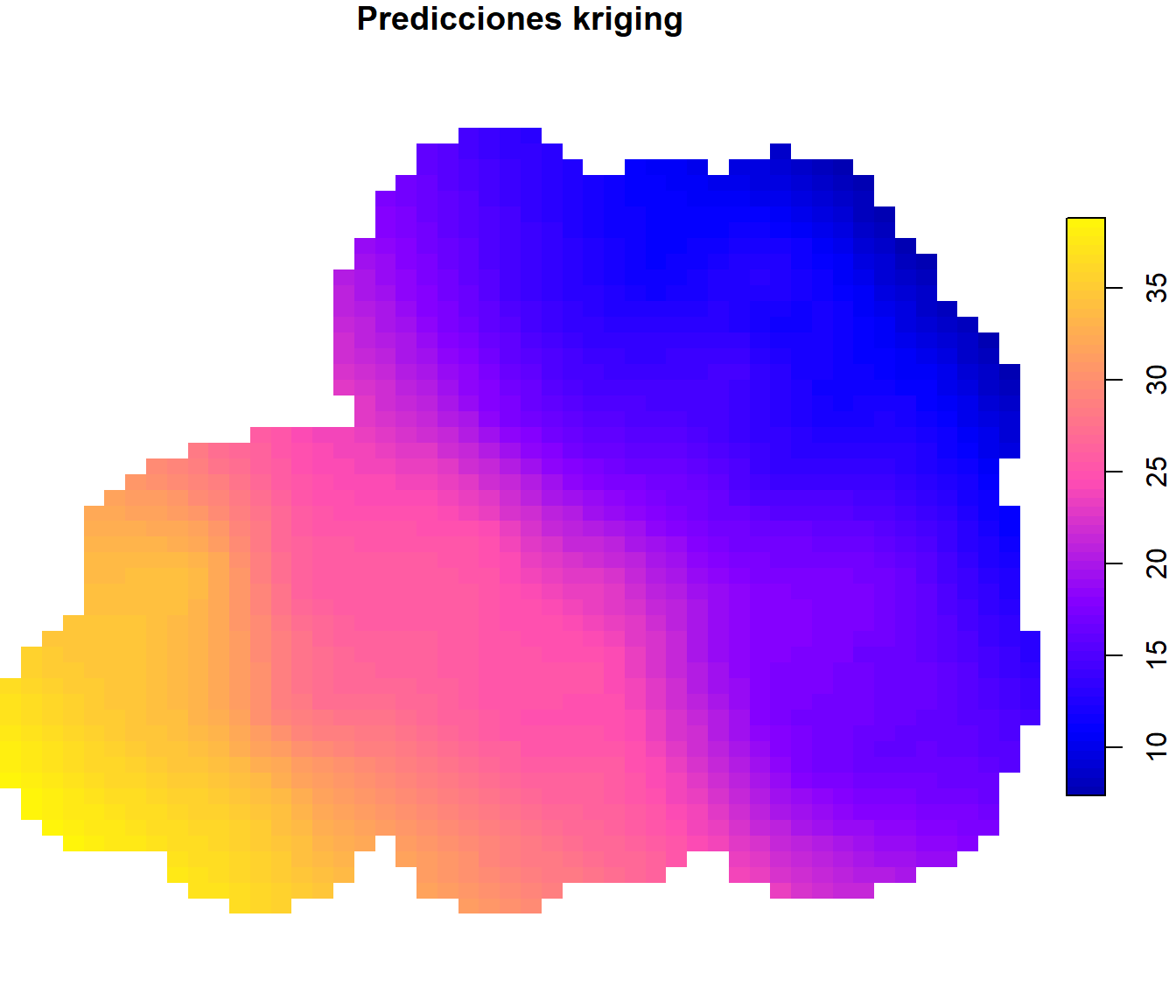
plot(grid["var1.var"], breaks = "equal", col = sf.colors(64), key.pos = 4,
main = "Varianzas kriging")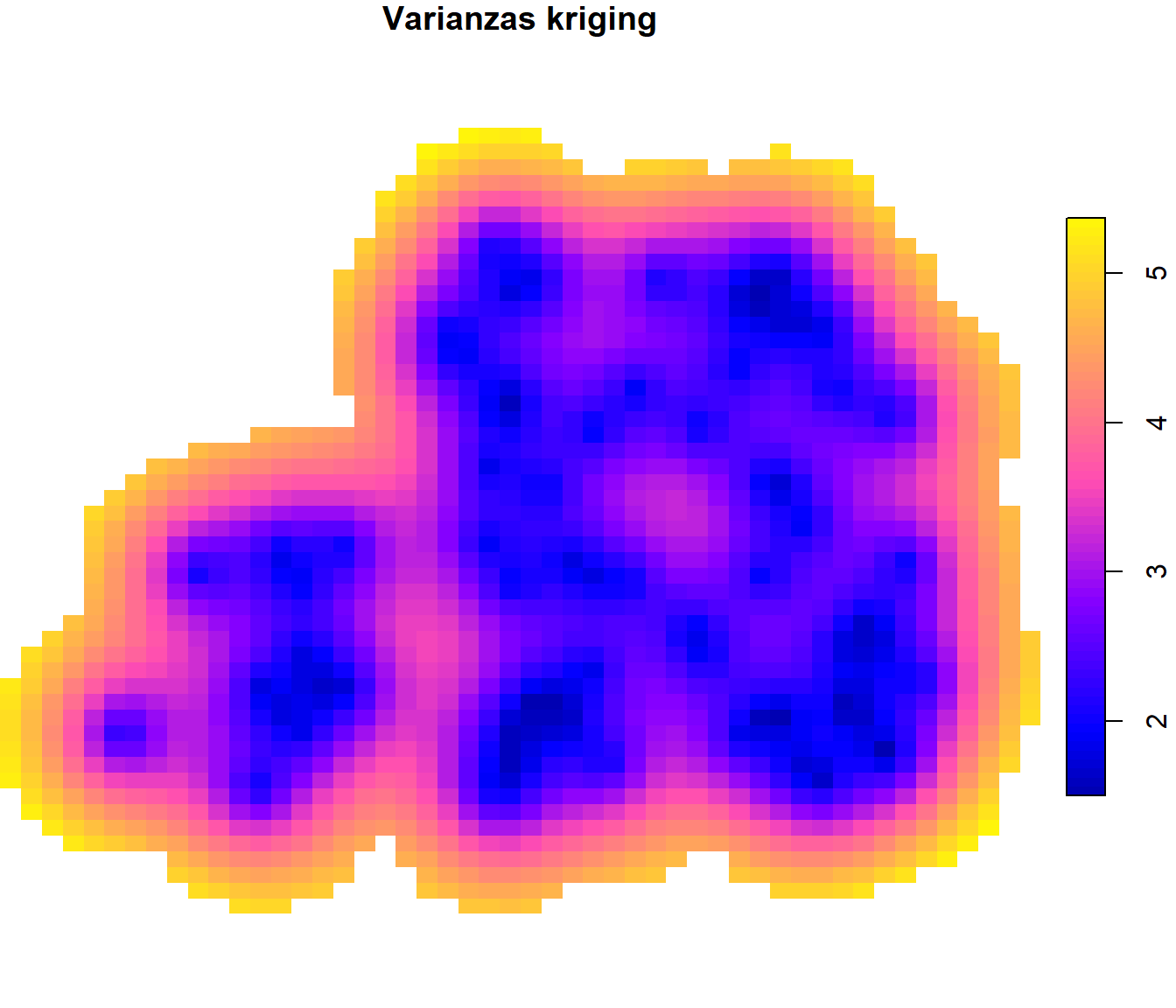
También podríamos emplear el paquete ggplot2:
library(ggplot2)
library(gridExtra)
p1 <- ggplot() + geom_stars(data = grid, aes(fill = var1.pred, x = x, y = y)) +
scale_fill_viridis_c() + geom_sf(data = aquifer_sf) +
coord_sf(lims_method = "geometry_bbox")
p2 <- ggplot() + geom_stars(data = grid, aes(fill = var1.var, x = x, y = y)) +
scale_fill_viridis_c() + geom_sf(data = aquifer_sf) +
coord_sf(lims_method = "geometry_bbox")
grid.arrange(p1, p2, ncol = 2)