2.5 Análisis exploratorio de datos espaciales

Como se comentó en la Sección 1.4, el primer paso para estimar las componentes del modelo, la tendencia \(\mu(\mathbf{s})\) y el semivariograma \(\gamma(\mathbf{h})\), es realizar un análisis exploratorio de los datos.

Normalmente comenzaremos por un análisis descriptivo de la respuesta. Sería deseable que su distribución fuese aproximadamente simétrica (de forma que los métodos basados en mínimos cuadrados sean adecuados). Si además la distribución es aproximadamente normal (después de eliminar la tendencia) tendría sentido emplear métodos basados en máxima verosimilitud (Sección 3.3.3) y los predictores kriging serían los más eficientes (Sección 4.5). Si su distribución es muy asimétrica se puede pensar en transformarla como punto de partida (aunque podría cambiarse posteriormente dependiendo del modelo final para la tendencia).

load("datos/aquifer.RData")
str(aquifer)
## 'data.frame':    85 obs. of  3 variables:
##  $ lon : num  42.78 -27.4 -1.16 -18.62 96.47 ...
##  $ lat : num  127.6 90.8 84.9 76.5 64.6 ...
##  $ head: num  1464 2553 2158 2455 1756 ...
library(sf)
aquifer_sf <- st_as_sf(aquifer, coords = c("lon", "lat"), agr = "constant")
z <- aquifer_sf$head/100
summary(z)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   10.24   15.48   17.97   20.02   25.40   35.71
hist(z, xlab = "piezometric-head", main = "", freq = FALSE)
lines(density(z), col = 'blue')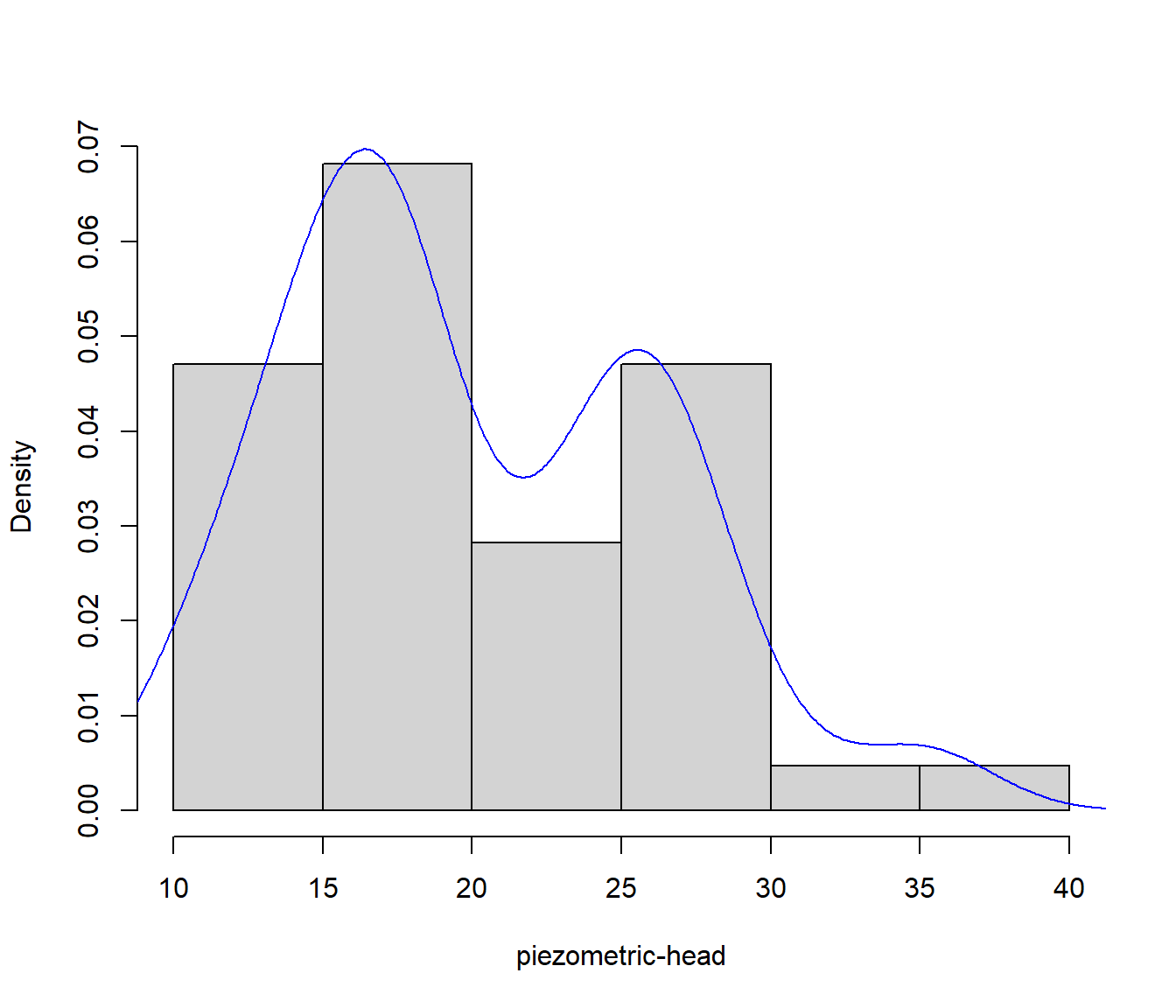
Distribución del nivel del agua subterránea en el acuífero Wolfcamp.

Figura 2.11: Distribución del nivel del agua subterránea en el acuífero Wolfcamp.

En un segundo paso se podría tener en cuenta las coordenadas espaciales. Por ejemplo, podríamos generar un gráfico de dispersión para ver si se observa algún patrón claro (lo que nos haría sospechar que la tendencia no es constante).

plot(aquifer_sf, pch = 20, cex = 3, breaks = "quantile", nbreaks = 4)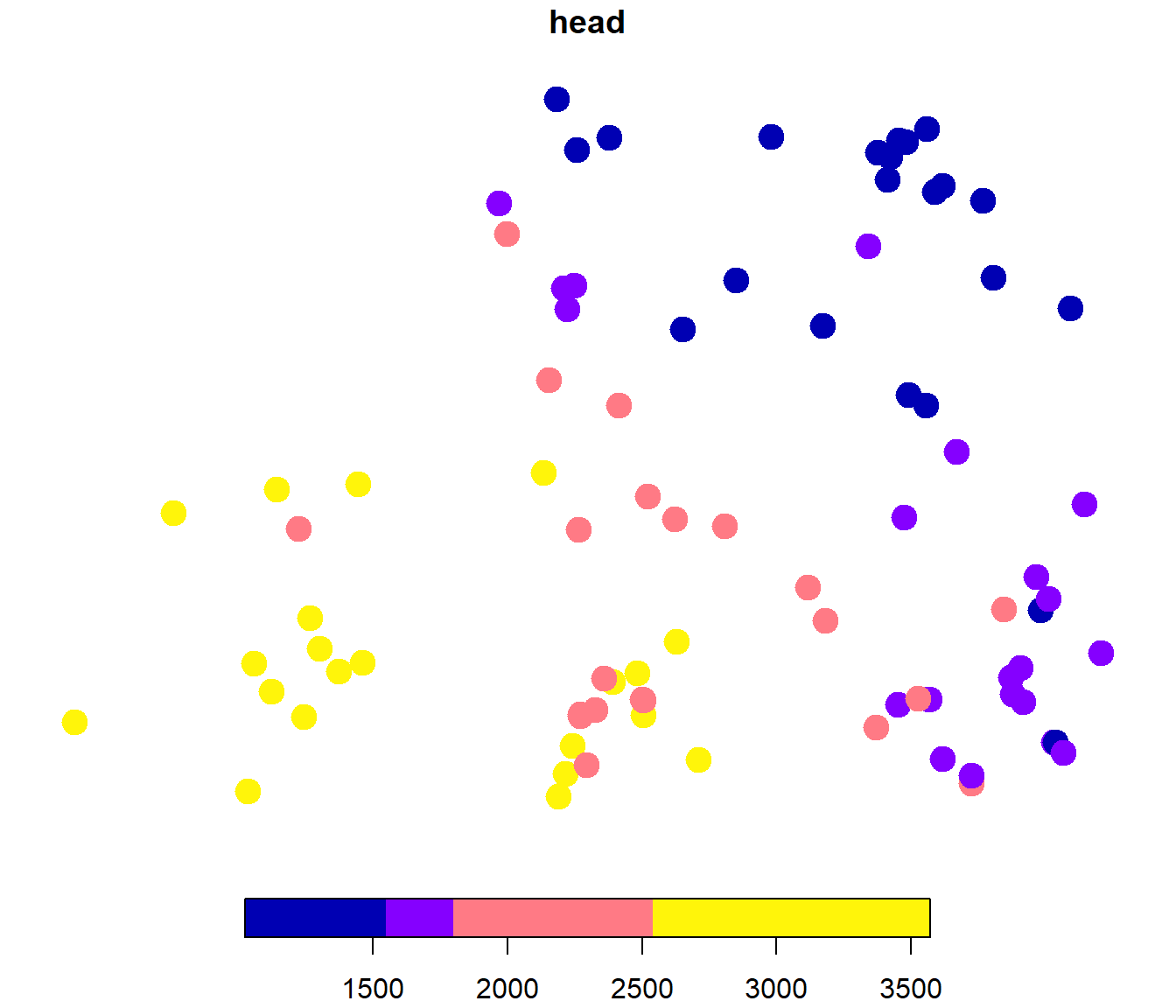
Distribución espacial de las observaciones del nivel del agua subterránea en el acuífero Wolfcamp.

Figura 2.12: Distribución espacial de las observaciones del nivel del agua subterránea en el acuífero Wolfcamp.

Gráficos de dispersión de la respuesta frente a las coordenadas nos pueden ayudar a determinar si hay una tendencia (al estilo de las funciones geoR::plot.geodata() o npsp::scattersplot()):

coord <- st_coordinates(aquifer_sf)
old.par <- par(mfrow = c(1, 2), omd = c(0.05, 0.95, 0.01, 0.95))
plot(coord[, 1], z, xlab = "x", ylab = "z")
lines(lowess(coord[, 1], z), lty = 2, lwd = 2, col = 'blue')
plot(coord[, 2], z, xlab = "y", ylab = "z")
lines(lowess(coord[, 2], z), lty = 2, lwd = 2, col = 'blue')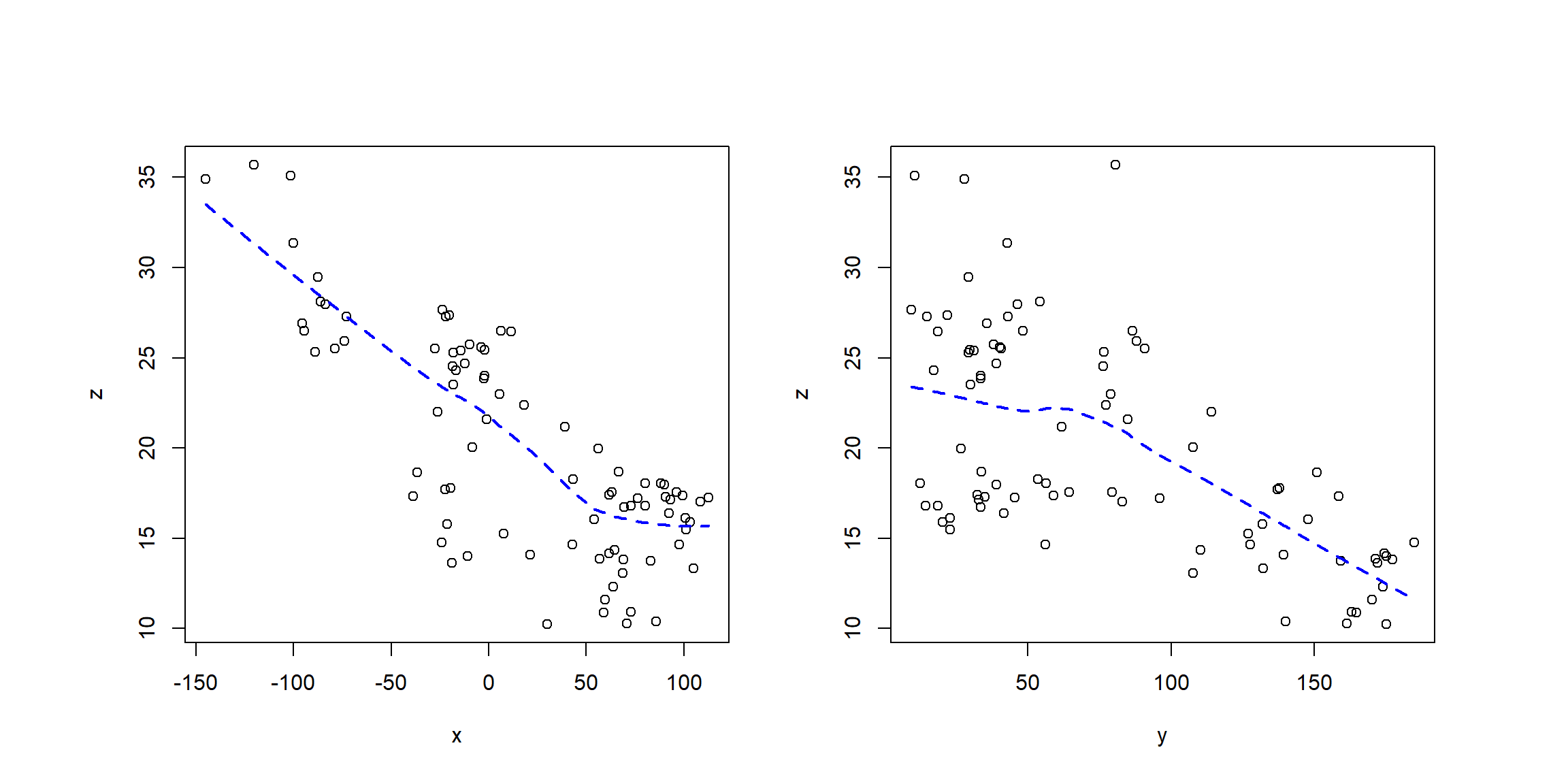
Gráficos de dispersión del nivel del agua subterránea frente a coordenadas (acuífero Wolfcamp).

Figura 2.13: Gráficos de dispersión del nivel del agua subterránea frente a coordenadas (acuífero Wolfcamp). 

par(old.par)

En este caso concreto parece que una tendencia lineal es adecuada.

Ejercicio 2.3 (Análisis exploratorio de la tendencia) Realizar un análisis exploratorio del conjunto de datos s100 del paquete geoR (que contiene una simulación de un proceso espacial estacionario, sin tendencia; ver Sección 3.1).

Ejercicio 2.4 (Análisis exploratorio con variables explicativas) Realizar un análisis exploratorio del conjunto de datos meuse_sf (almacenado en el archivo st_meuse.RData; ver Figura 2.1) considerando como respuesta la concentración de zinc y como variables explicativas, además de las coordenadas espaciales, las variables que comparte con la rejilla meuse_grid (y que se podrían emplear en la predicción kriging; Capítulo 4).

Realizar también un análisis exploratorio multivariante, considerando la respuesta y el resto de variables explicativas (que podrían considerarse realizaciones de otros procesos espaciales y emplearlas para predicción multivariante, cokriging; Capítulo 5).

Para el análisis exploratorio de la dependencia se suelen emplear las semivarianzas muestrales o los estimadores experimentales del variograma, como se describe en la Sección 3.1.