D.3 Modelado de la dependencia

D.3.1 Estimación experimental del variograma

Como se muestra en la Sección 3.1, las estimaciones empíricas del semivariograma se obtienen con la función variogram().

En el caso de tendencia no constante la estimación del variograma se haría a partir de los residuos, Sección 3.3.2, especificando la fórmula del modelo de tendencia como primer argumento de la función variogram() (si la tendencia es constante, la fórmula sería del tipo respuesta ~ 1, y la estimación del variograma se obtendría directamente de las observaciones).

library(gstat)
# maxlag <- 0.5*sqrt(sum(diff(matrix(st_bbox(aquifer_sf), nrow = 2, byrow = TRUE))^2))
maxlag <- 150
vario <- variogram(head ~ lon + lat, aquifer_sf, cutoff = maxlag)
# por defecto considera 15 saltos (width = cutoff/15)

Habría que determinar el número de saltos (por defecto 15, width = cutoff/15) y el salto máximo (por defecto 1/3 del máximo salto posible) para la estimación del variograma (nos interesaría que fuese lo mejor posible cerca del origen). Para seguir las recomendaciones de Journel y Huijbregts (1978), de considerar a lo sumo hasta la mitad del máximo salto posible (podría ser preferible menor) y saltos con aportaciones de al menos 30 pares de datos (se puede relajar cerca del origen), podemos representar las estimaciones junto con el número de aportaciones:

plot(vario, plot.numbers = TRUE)

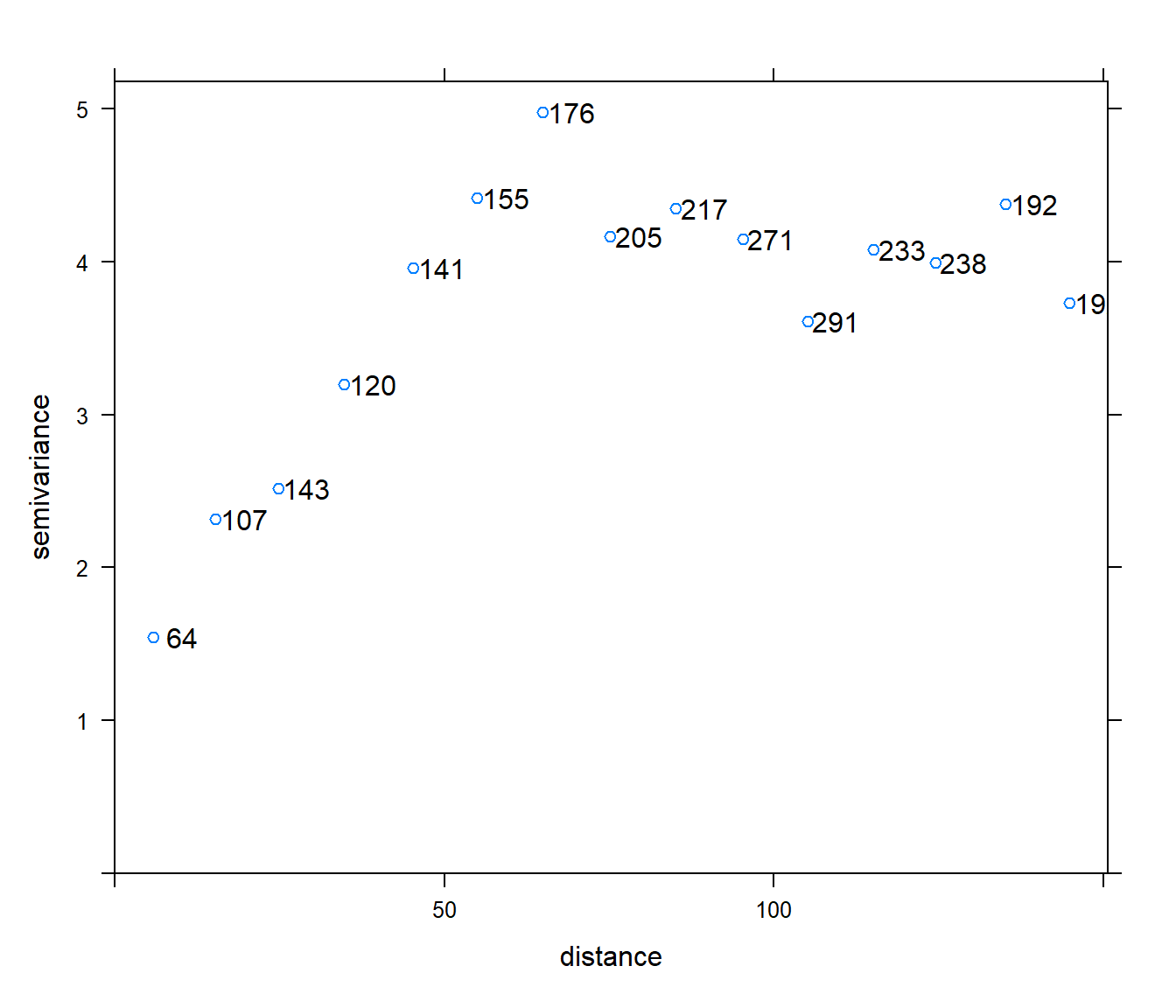
Si hay datos atípicos sería preferible emplear una versión robusta de este estimador. Además, estamos asumiendo isotropía, aunque lo ideal sería asegurarse de que es una hipótesis razonable (ver comentarios al final de la Sección 3.1 y Sección 3.2.2).

D.3.2 Ajuste de un modelo válido

El paso final en el modelado es el ajuste por WLS de un modelo válido (Sección 3.3.1; la recomendación es emplear pesos inversamente proporcionales a la varianza fit.method = 2). En este caso un modelo de variograma esférico parece razonable:

modelo <- vgm(model = "Sph", nugget = NA) # Valores iniciales por defecto
# modelo <- vgm(psill = 3, model = "Sph", range = 75, nugget = 0) # Valores iniciales
fit <- fit.variogram(vario, modelo, fit.method = 2)

NOTA: Si aparecen problemas de convergencia se puede probar a cambiar los valores iniciales de los parámetros.

Imprimiendo el resultado del ajuste obtenemos las estimaciones de los parámetros, que podríamos interpretar (ver Sección 1.3 y Sección 4.5.2):

fit

##   model    psill    range
## 1   Nug 1.095133  0.00000
## 2   Sph 3.044034 63.39438

nugget <- fit$psill[1]
sill <- nugget + fit$psill[2]
range <- fit$range[2]

NOTA: Cuidado, en el caso de un variograma exponencial, el parámetro que aparece como range es un parámetro de escala proporcional al verdadero rango práctico (tres veces ese valor).

Si quisiésemos comparar el ajuste de distintos modelos se podría considerar el valor mínimo de la función objetivo WLS, almacenado como un atributo del resultado (aunque la recomendación sería emplear validación cruzada):

attr(fit, "SSErr")

## [1] 8.424426

En cualquier caso la recomendación es analizar gráficamente el ajuste de los modelos. Para representar las estimaciones empíricas junto con un único ajuste, se podría emplear plot.gstatVariogram():

# Cuidado con plot.variogramModel() si se pretende añadir elementos
# plot(fit, cutoff = maxlag, ylim = c(0, 4.5))
# with(vario,  points(dist, gamma))
plot(vario, fit)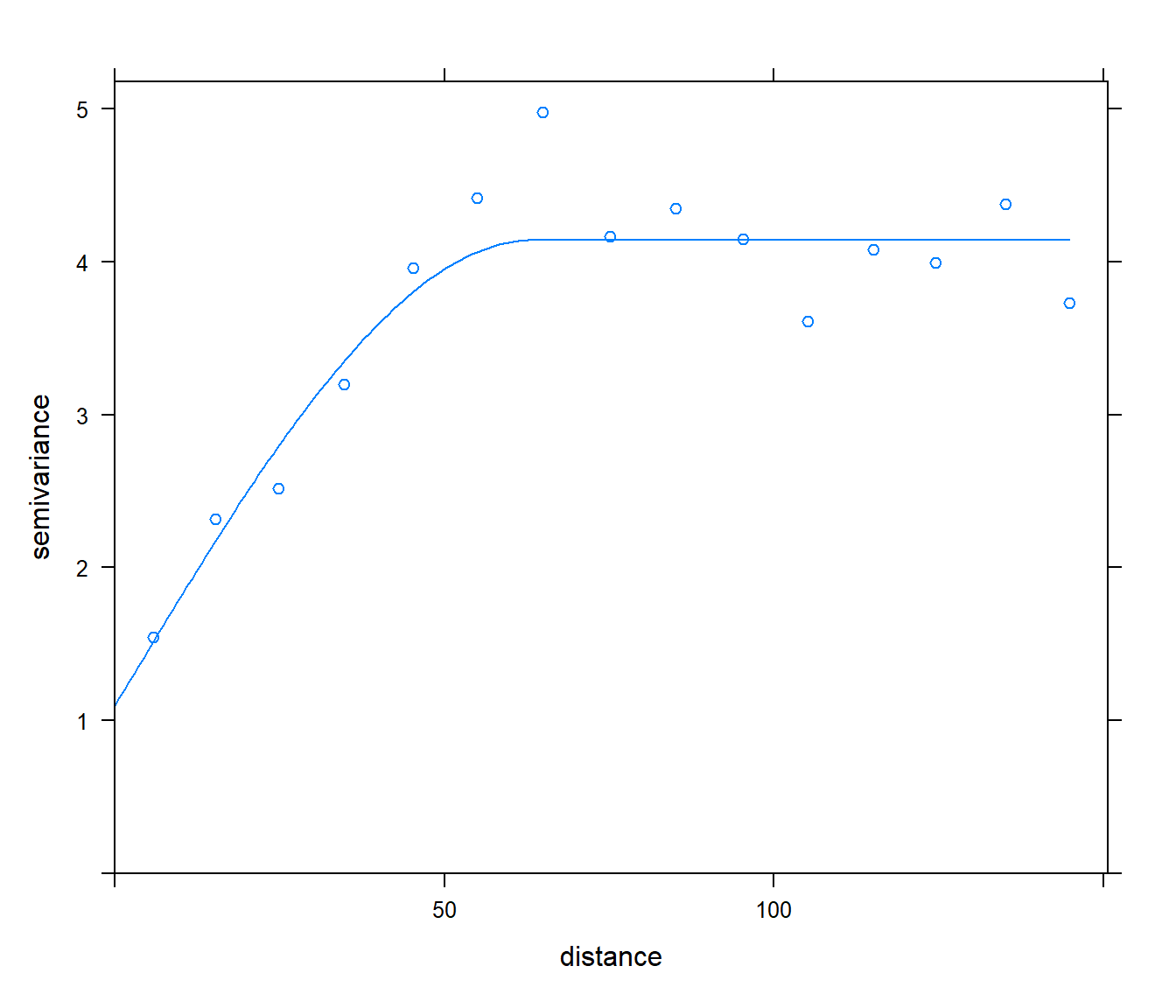

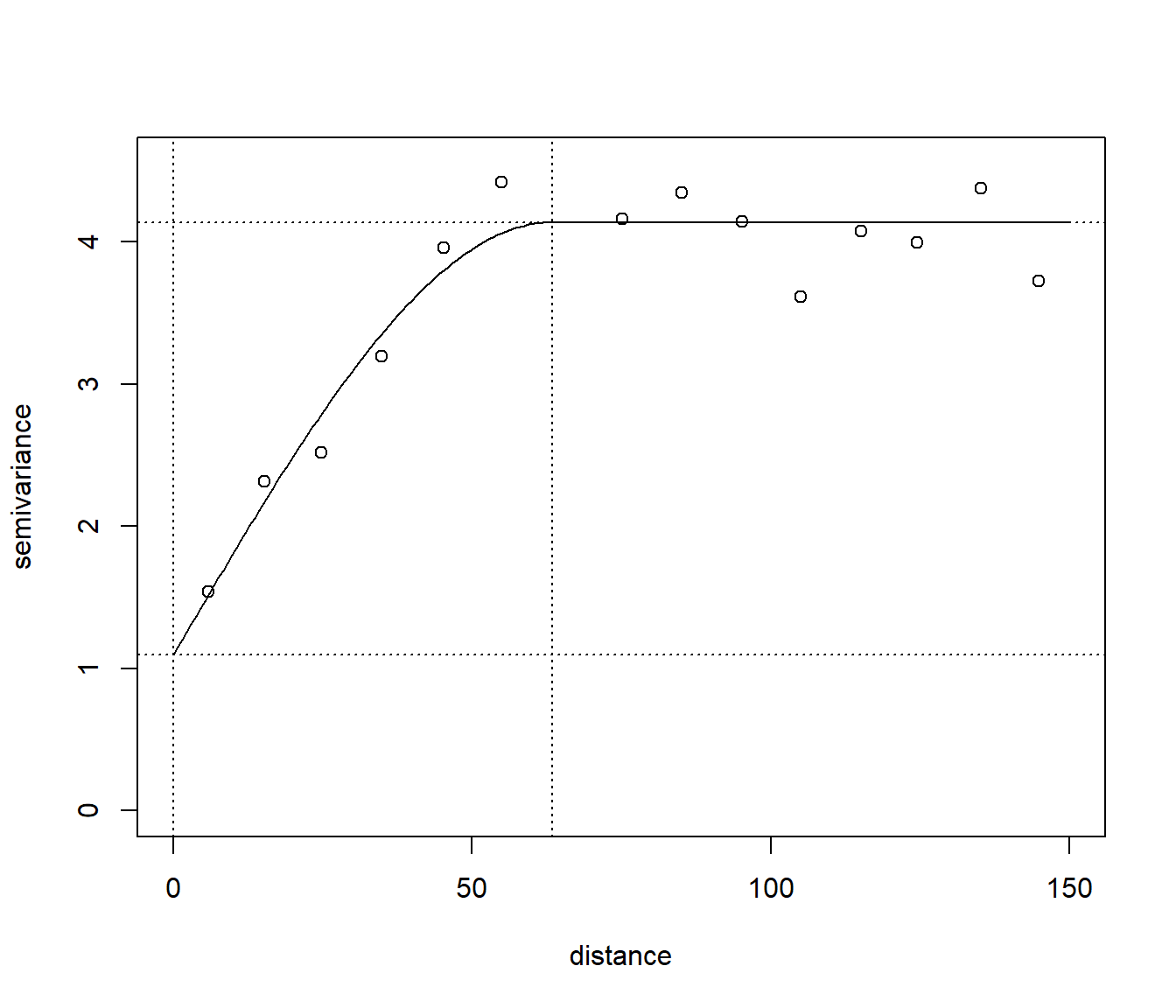
Para añadir más elementos mejor hacerlo “a mano”:

plot(vario$dist, vario$gamma, xlab = "distance", ylab =  "semivariance", 
     xlim = c(0, max(range*1.1, maxlag)), ylim = c(0, sill*1.1))
lines(variogramLine(fit, maxdist = max(range*1.1, maxlag)))
abline(v = 0, lty = 3)
abline(v = range, lty = 3)
abline(h = nugget, lty = 3)
abline(h = sill, lty = 3)