D.5 Validación cruzada
Para realizar una diagnosis del modelo de tendencia y variograma (y para seleccionar parámetros o comparar modelos) podemos emplear la técnica de validación cruzada Sección 4.6, mediante la función krige.cv().
Por defecto emplea LOOCV y puede requerir de mucho tiempo de computación (no está implementado eficientemente en gtsat):
system.time(cv <- krige.cv(formula = head ~ lon + lat, locations = aquifer_sf,
model = fit))## user system elapsed
## 0.56 0.02 0.58str(cv)## Classes 'sf' and 'data.frame': 85 obs. of 7 variables:
## $ var1.pred: num 15 23.5 22.9 24.6 17 ...
## $ var1.var : num 3.08 2.85 2.32 2.81 2.05 ...
## $ observed : num 14.6 25.5 21.6 24.6 17.6 ...
## $ residual : num -0.3357 1.9962 -1.3101 -0.0792 0.5478 ...
## $ zscore : num -0.1914 1.1821 -0.8608 -0.0472 0.3829 ...
## $ fold : int 1 2 3 4 5 6 7 8 9 10 ...
## $ geometry :sfc_POINT of length 85; first list element: 'XY' num 42.8 127.6
## - attr(*, "sf_column")= chr "geometry"
## - attr(*, "agr")= Factor w/ 3 levels "constant","aggregate",..: NA NA NA NA NA NA
## ..- attr(*, "names")= chr [1:6] "var1.pred" "var1.var" "observed" "residual" ...Si el número de observaciones es grande puede ser preferible emplear k-fold CV (y como la partición en grupos es aleatoria se recomendaría fijar previamente la semilla de aleatorización):
set.seed(1)
system.time(cv <- krige.cv(formula = head ~ lon + lat, locations = aquifer_sf,
model = fit, nfold = 10))## user system elapsed
## 0.14 0.02 0.16Para seleccionar modelos podemos considerar distintas medidas, implementadas en la siguiente función:
summary_cv <- function(cv.data, na.rm = FALSE,
tol = sqrt(.Machine$double.eps)) {
err <- cv.data$residual # Errores
obs <- cv.data$observed
z <- cv.data$zscore
w <- 1/pmax(cv.data$var1.var, tol) # Ponderación según varianza kriging
if(na.rm) {
is.a <- !is.na(err)
err <- err[is.a]
obs <- obs[is.a]
z <- z[is.a]
w <- w[is.a]
}
perr <- 100*err/pmax(obs, tol) # Errores porcentuales
return(c(
# Medidas de error tradicionales
me = mean(err), # Error medio
rmse = sqrt(mean(err^2)), # Raíz del error cuadrático medio
mae = mean(abs(err)), # Error absoluto medio
mpe = mean(perr), # Error porcentual medio
mape = mean(abs(perr)), # Error porcentual absoluto medio
r.squared = 1 - sum(err^2)/sum((obs - mean(obs))^2), # Pseudo R-cuadrado
# Medidas de error que tienen en cuenta la varianza kriging
dme = mean(z), # Error estandarizado medio
dmse = sqrt(mean(z^2)), # Error cuadrático medio adimensional
rwmse = sqrt(weighted.mean(err^2, w)) # Raíz del ECM ponderado
))
}
summary_cv(cv)## me rmse mae mpe mape r.squared
## 0.058039856 1.788446500 1.407874022 -0.615720059 7.852363328 0.913398424
## dme dmse rwmse
## 0.001337332 1.118978878 1.665958815Las tres últimas medidas tienen en cuenta la estimación de la varianza kriging. El valor del error cuadrático medio adimensional debería ser próximo a 1 si hay concordancia entre las varianzas kriging y las varianzas observadas.
Para detectar datos atípicos, o problemas con el modelo, podemos generar distintos gráficos. Por ejemplo, gráficos de dispersión de valores observados o residuos estándarizados frente a predicciones:
old_par <- par(mfrow = c(1, 2))
plot(observed ~ var1.pred, data = cv, xlab = "Predicción", ylab = "Observado")
abline(a = 0, b = 1, col = "blue")
plot(zscore ~ var1.pred, data = cv, xlab = "Predicción", ylab = "Residuo estandarizado")
abline(h = c(-3, -2, 0, 2, 3), lty = 3)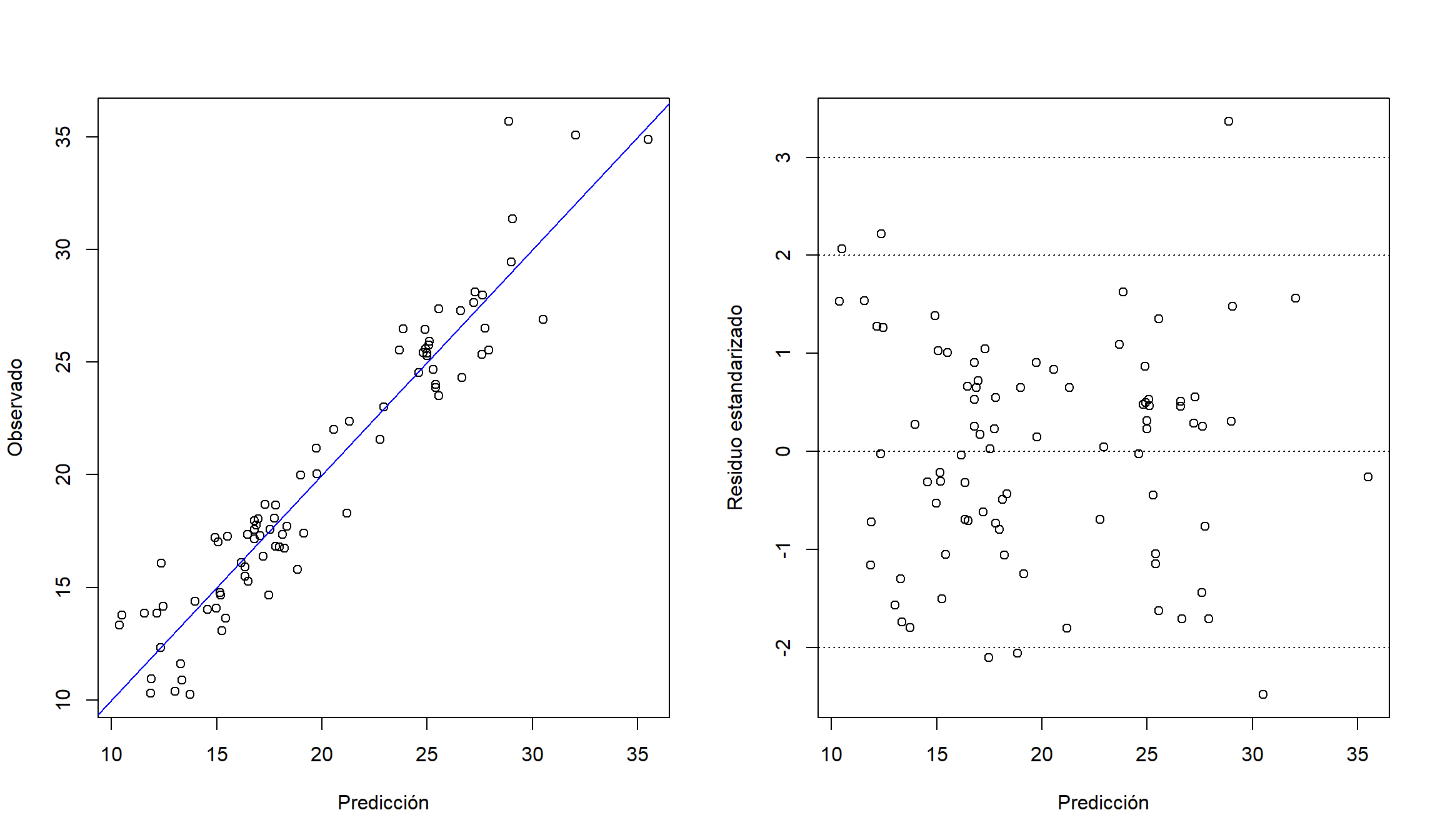
par(old_par)Gráficos con la distribución espacial de los residuos:
plot(cv["residual"], pch = 20, cex = 2, breaks = "quantile", nbreaks = 4)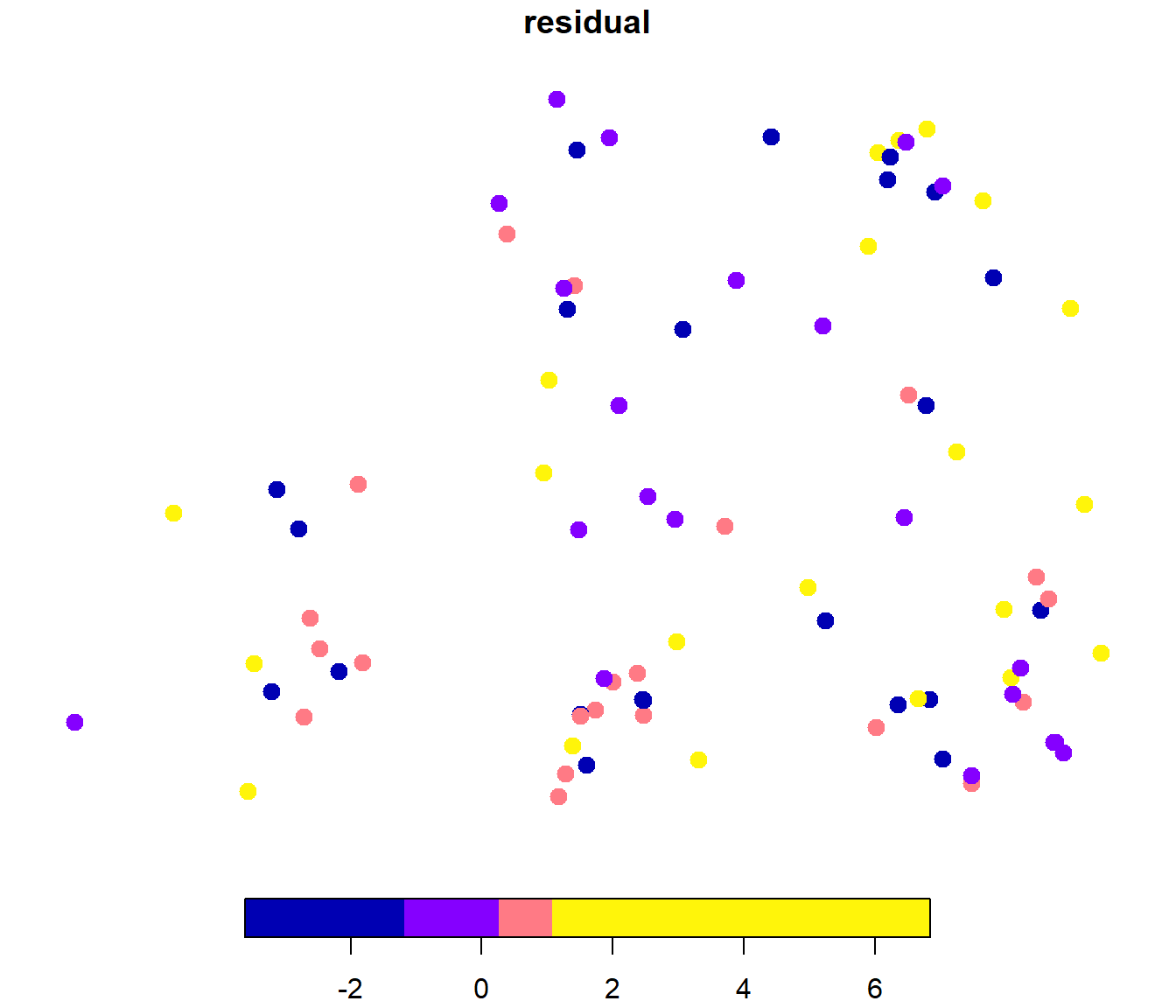
plot(cv["zscore"], pch = 20, cex = 2)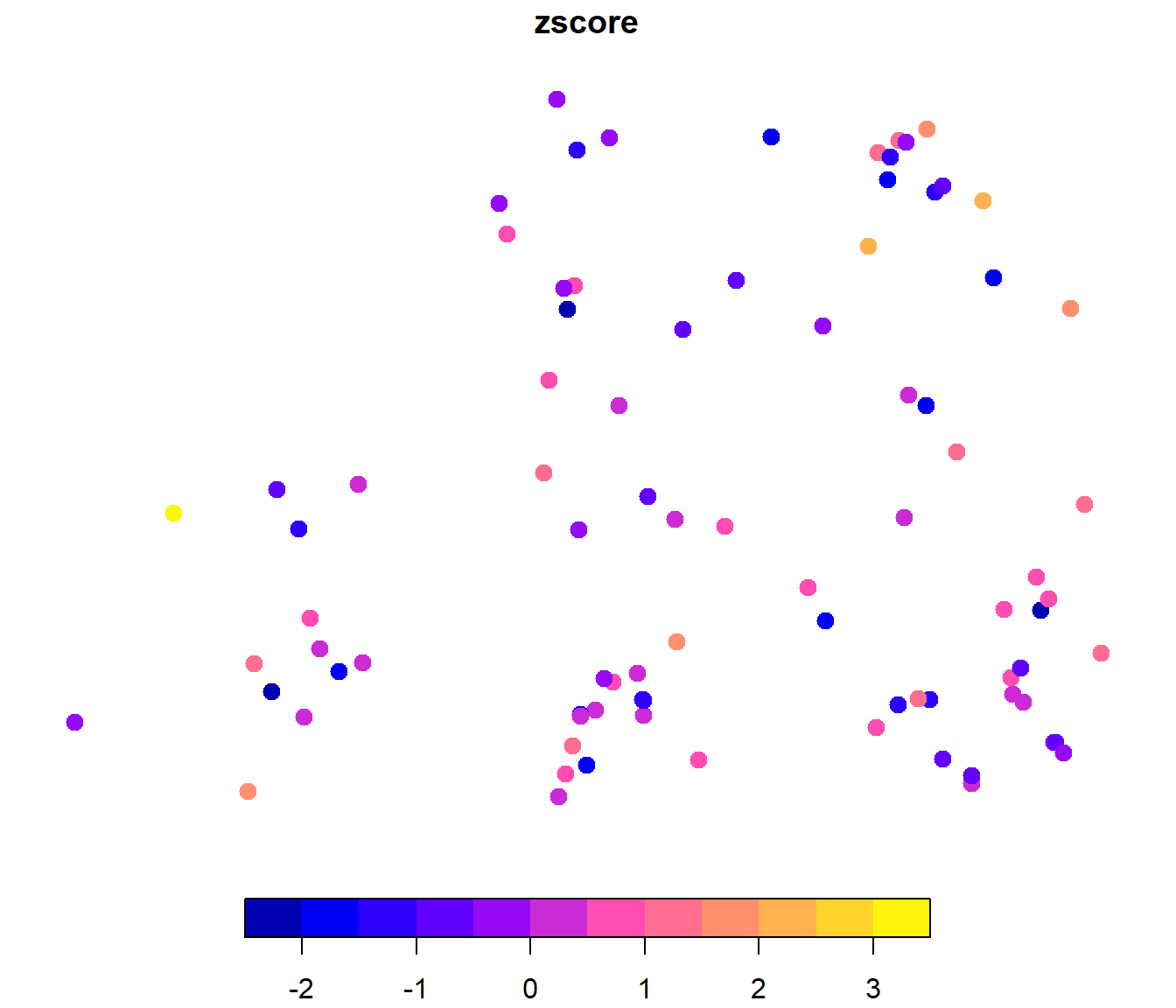
Además de los gráficos estándar para analizar la distribución de los residuos estandarizados o detectar atípicos:
# Histograma
old_par <- par(mfrow = c(1, 3))
hist(cv$zscore, freq = FALSE)
lines(density(cv$zscore), col = "blue")
# Gráfico de normalidad
qqnorm(cv$zscore)
qqline(cv$zscore, col = "blue")
# Boxplot
car::Boxplot(cv$zscore, ylab = "Residuos estandarizados")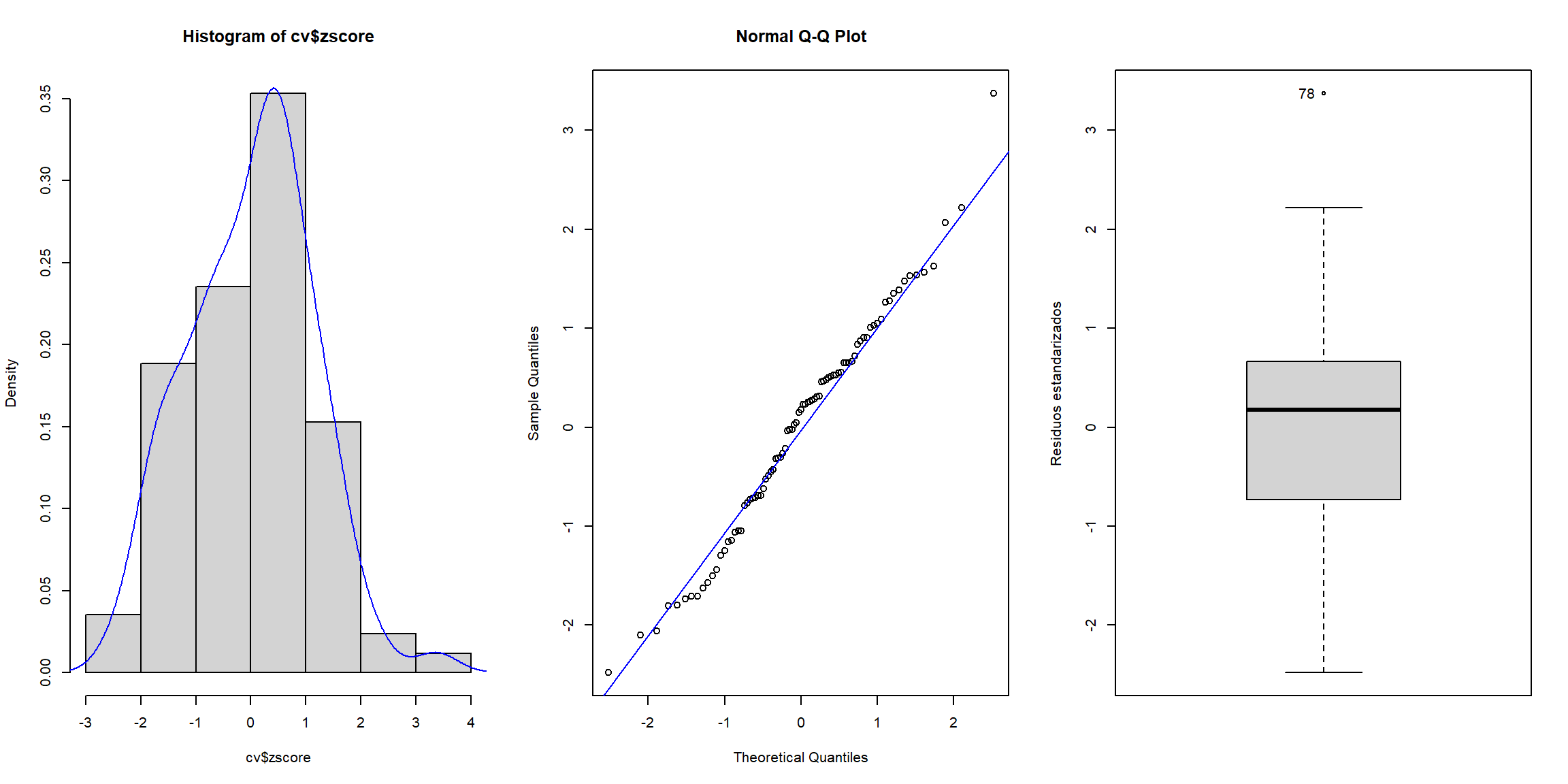
## [1] 78par(old_par)