2.2 Introducción al paquete sf
El modelo de geometrías de características simples (o rasgos simples) es un estándar (ISO 19125) desarrollado por el Open Geospatial Consortium (OGC) para formas geográficas vectoriales, que ha sido adoptado por gran cantidad de software geográfico (entre otros por GeoJSON, ArcGIS, QGIS, PostGIS, MySQL Spatial Extensions, Microsoft SQL Server…).
Como ya se comentó, este tipo de datos espaciales está implementado en R en el paquete sf.
Los objetos principales, del tipo sf, son extensiones de data.frame (o tibble) y como mínimo contienen una columna denominada simple feature geometry list column que contiene la geometría de cada observación (se trata de una columna tipo list).
Cada fila, incluyendo la geometría y otras posibles variables (denominados atributos de la geometría), se considera una característica simple (SF).
library(sf)
nc <- st_read(system.file("shape/nc.shp", package="sf"), quiet = TRUE)
nc <- nc[c(5, 9:15)]
nc## Simple feature collection with 100 features and 7 fields
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: -84.32385 ymin: 33.88199 xmax: -75.45698 ymax: 36.58965
## Geodetic CRS: NAD27
## First 10 features:
## NAME BIR74 SID74 NWBIR74 BIR79 SID79 NWBIR79
## 1 Ashe 1091 1 10 1364 0 19
## 2 Alleghany 487 0 10 542 3 12
## 3 Surry 3188 5 208 3616 6 260
## 4 Currituck 508 1 123 830 2 145
## 5 Northampton 1421 9 1066 1606 3 1197
## 6 Hertford 1452 7 954 1838 5 1237
## 7 Camden 286 0 115 350 2 139
## 8 Gates 420 0 254 594 2 371
## 9 Warren 968 4 748 1190 2 844
## 10 Stokes 1612 1 160 2038 5 176
## geometry
## 1 MULTIPOLYGON (((-81.47276 3...
## 2 MULTIPOLYGON (((-81.23989 3...
## 3 MULTIPOLYGON (((-80.45634 3...
## 4 MULTIPOLYGON (((-76.00897 3...
## 5 MULTIPOLYGON (((-77.21767 3...
## 6 MULTIPOLYGON (((-76.74506 3...
## 7 MULTIPOLYGON (((-76.00897 3...
## 8 MULTIPOLYGON (((-76.56251 3...
## 9 MULTIPOLYGON (((-78.30876 3...
## 10 MULTIPOLYGON (((-80.02567 3...str(nc)## Classes 'sf' and 'data.frame': 100 obs. of 8 variables:
## $ NAME : chr "Ashe" "Alleghany" "Surry" "Currituck" ...
## $ BIR74 : num 1091 487 3188 508 1421 ...
## $ SID74 : num 1 0 5 1 9 7 0 0 4 1 ...
## $ NWBIR74 : num 10 10 208 123 1066 ...
## $ BIR79 : num 1364 542 3616 830 1606 ...
## $ SID79 : num 0 3 6 2 3 5 2 2 2 5 ...
## $ NWBIR79 : num 19 12 260 145 1197 ...
## $ geometry:sfc_MULTIPOLYGON of length 100; first list element: List of 1
## ..$ :List of 1
## .. ..$ : num [1:27, 1:2] -81.5 -81.5 -81.6 -81.6 -81.7 ...
## ..- attr(*, "class")= chr [1:3] "XY" "MULTIPOLYGON" "sfg"
## - attr(*, "sf_column")= chr "geometry"
## - attr(*, "agr")= Factor w/ 3 levels "constant","aggregate",..: NA NA NA NA NA NA NA
## ..- attr(*, "names")= chr [1:7] "NAME" "BIR74" "SID74" "NWBIR74" ...El nombre de la columna de geometrías está almacenado en el atributo "sf_column" del objeto y se puede acceder a ella mediante la función st_geometry() (además de poder emplear los procedimientos habituales para acceder a los componentes de un data.frame).
Esta columna es un objeto de tipo sfc (simple feature geometry list column), descritos más adelante.
# geom_name <- attr(nc, "sf_column")
# nc[, geom_name]; nc[[geom_name]]
# nc$geometry
st_geometry(nc)## Geometry set for 100 features
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: -84.32385 ymin: 33.88199 xmax: -75.45698 ymax: 36.58965
## Geodetic CRS: NAD27
## First 5 geometries:## MULTIPOLYGON (((-81.47276 36.23436, -81.54084 3...## MULTIPOLYGON (((-81.23989 36.36536, -81.24069 3...## MULTIPOLYGON (((-80.45634 36.24256, -80.47639 3...## MULTIPOLYGON (((-76.00897 36.3196, -76.01735 36...## MULTIPOLYGON (((-77.21767 36.24098, -77.23461 3...En este paquete, todos los métodos y funciones que operan sobre datos espaciales comienzan por st_ (spatial type; siguiendo la implementación de PostGIS):
methods(class="sf")## [1] $<- [ [[<-
## [4] aggregate anti_join arrange
## [7] as.data.frame cbind coerce
## [10] dbDataType dbWriteTable distinct
## [13] dplyr_reconstruct filter full_join
## [16] gather group_by group_split
## [19] identify idw initialize
## [22] inner_join krige krige.cv
## [25] left_join merge mutate
## [28] nest pivot_longer plot
## [31] print rbind rename
## [34] right_join rowwise sample_frac
## [37] sample_n select semi_join
## [40] separate separate_rows show
## [43] slice slotsFromS3 spread
## [46] st_agr st_agr<- st_area
## [49] st_as_s2 st_as_sf st_as_stars
## [52] st_bbox st_boundary st_buffer
## [55] st_cast st_centroid st_collection_extract
## [58] st_convex_hull st_coordinates st_crop
## [61] st_crs st_crs<- st_difference
## [64] st_filter st_geometry st_geometry<-
## [67] st_inscribed_circle st_interpolate_aw st_intersection
## [70] st_intersects st_is st_is_valid
## [73] st_join st_line_merge st_m_range
## [76] st_make_valid st_nearest_points st_node
## [79] st_normalize st_point_on_surface st_polygonize
## [82] st_precision st_reverse st_sample
## [85] st_segmentize st_set_precision st_shift_longitude
## [88] st_simplify st_snap st_sym_difference
## [91] st_transform st_transform_proj st_triangulate
## [94] st_union st_voronoi st_wrap_dateline
## [97] st_write st_z_range st_zm
## [100] summarise transform transmute
## [103] ungroup unite unnest
## see '?methods' for accessing help and source codeLos objetos geométricos básicos son del tipo sfg (simple feature geometry) que contienen la geometría de una única característica definida a partir de puntos en dos (XY), tres (XYZ, XYM) o cuatro dimensiones (XYZM).
Admite los 17 tipos de geometrías simples del estándar, pero de forma completa los 7 tipos básicos:
| Tipo | Description | Creación |
|---|---|---|
POINT, MULTIPOINT |
Punto o conjunto de puntos | st_point(), st_multipoint() |
LINESTRING, MULTILINESTRING |
Línea o conjunto de líneas | st_linestring(), st_multilinestring() |
POLYGON, MULTIPOLYGON |
Polígono6 o conjunto de polígonos | st_polygon(), st_multipolygon() |
GEOMETRYCOLLECTION |
Conjunto de geometrías de los tipos anteriores | st_geometrycollection() |
Las geometrías se imprimen empleando la representación well-known text (WKT) del estándar (se exportan empleando la representación well-known binary, WKB).
nc$geometry[[1]]## MULTIPOLYGON (((-81.47276 36.23436, -81.54084 36.27251, -81.56198 36.27359, -81.63306 36.34069, -81.74107 36.39178, -81.69828 36.47178, -81.7028 36.51934, -81.67 36.58965, -81.3453 36.57286, -81.34754 36.53791, -81.32478 36.51368, -81.31332 36.4807, -81.26624 36.43721, -81.26284 36.40504, -81.24069 36.37942, -81.23989 36.36536, -81.26424 36.35241, -81.32899 36.3635, -81.36137 36.35316, -81.36569 36.33905, -81.35413 36.29972, -81.36745 36.2787, -81.40639 36.28505, -81.41233 36.26729, -81.43104 36.26072, -81.45289 36.23959, -81.47276 36.23436)))Los objetos básicos sfg (normalmente del mismo tipo) se pueden combinar en un objeto sfc (simple feature geometry list column) mediante la función st_sfg().
Estos objetos pueden incorporar un sistema de referencia de coordenadas (por defecto NA_crs_), descritos en la Sección 2.2.1.
Posteriormente se puede crear un objeto sf mediante la función st_sf().
p1 <- st_point(c(-8.395835, 43.37087))
p2 <- st_point(c(-7.555851, 43.01208))
p3 <- st_point(c(-7.864641, 42.34001))
p4 <- st_point(c(-8.648053, 42.43362))
sfc <- st_sfc(list(p1, p2, p3, p4))
cprov <- st_sf(names = c('Coruña (A)', 'Lugo', 'Ourense', 'Pontevedra'),
geom = sfc)
cprov## Simple feature collection with 4 features and 1 field
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: -8.648053 ymin: 42.34001 xmax: -7.555851 ymax: 43.37087
## CRS: NA
## names geom
## 1 Coruña (A) POINT (-8.395835 43.37087)
## 2 Lugo POINT (-7.555851 43.01208)
## 3 Ourense POINT (-7.864641 42.34001)
## 4 Pontevedra POINT (-8.648053 42.43362)Esta forma de proceder puede resultar de interés cuando se construyen geometrías tipo líneas o polígonos, pero en el caso de datos puntuales (las observaciones habituales en geoestadística), resulta mucho más cómodo emplear un data.frame que incluya las coordenadas en columnas y convertirlo a un objeto sf mediante la función st_as_sf().
Ejercicio 2.1 (Creación de una columna de geometrías) Crear una geometría (un objeto sfc) formada por: dos puntos en las posiciones
(1,5) y (5,5), una línea entre los puntos (1,1) y (5,1), y un polígono, con vértices
{(0,0), (6,0), (6,6), (0,6), (0,0)} y con un agujero con vértices {(2,2), (2,4),
(4,4), (4,2), (2,2)} (NOTA: consultar la ayuda ?st, puede resultar cómodo emplear
matrix(... , ncol = 2, byrow = TRUE)).
Como ejemplo consideraremos el conjunto de datos meuse del paquete sp que contiene concentraciones de metales pesados, junto con otras variables del terreno, en una zona de inundación del río Meuse (cerca de Stein, Holanda)7 (ver Figura 2.1).
data(meuse, package="sp")
str(meuse)## 'data.frame': 155 obs. of 14 variables:
## $ x : num 181072 181025 181165 181298 181307 ...
## $ y : num 333611 333558 333537 333484 333330 ...
## $ cadmium: num 11.7 8.6 6.5 2.6 2.8 3 3.2 2.8 2.4 1.6 ...
## $ copper : num 85 81 68 81 48 61 31 29 37 24 ...
## $ lead : num 299 277 199 116 117 137 132 150 133 80 ...
## $ zinc : num 1022 1141 640 257 269 ...
## $ elev : num 7.91 6.98 7.8 7.66 7.48 ...
## $ dist : num 0.00136 0.01222 0.10303 0.19009 0.27709 ...
## $ om : num 13.6 14 13 8 8.7 7.8 9.2 9.5 10.6 6.3 ...
## $ ffreq : Factor w/ 3 levels "1","2","3": 1 1 1 1 1 1 1 1 1 1 ...
## $ soil : Factor w/ 3 levels "1","2","3": 1 1 1 2 2 2 2 1 1 2 ...
## $ lime : Factor w/ 2 levels "0","1": 2 2 2 1 1 1 1 1 1 1 ...
## $ landuse: Factor w/ 15 levels "Aa","Ab","Ag",..: 4 4 4 11 4 11 4 2 2 15 ...
## $ dist.m : num 50 30 150 270 380 470 240 120 240 420 ...# ?meuse
# Sistema de coordenadas Rijksdriehoek (RDH) (Netherlands topographical)
# https://epsg.io/28992 # EPSG:28992
meuse_sf <- st_as_sf(meuse, coords = c("x", "y"), crs = 28992, agr = "constant")
# Rio Meuse
data(meuse.riv, package="sp")
str(meuse.riv)## num [1:176, 1:2] 182004 182137 182252 182315 182332 ...meuse_riv <- st_sfc(st_polygon(list(meuse.riv)), crs = 28992)
# Rejilla
data(meuse.grid, package="sp")
str(meuse.grid)## 'data.frame': 3103 obs. of 7 variables:
## $ x : num 181180 181140 181180 181220 181100 ...
## $ y : num 333740 333700 333700 333700 333660 ...
## $ part.a: num 1 1 1 1 1 1 1 1 1 1 ...
## $ part.b: num 0 0 0 0 0 0 0 0 0 0 ...
## $ dist : num 0 0 0.0122 0.0435 0 ...
## $ soil : Factor w/ 3 levels "1","2","3": 1 1 1 1 1 1 1 1 1 1 ...
## $ ffreq : Factor w/ 3 levels "1","2","3": 1 1 1 1 1 1 1 1 1 1 ...meuse_grid <- st_as_sf(meuse.grid, coords = c("x", "y"),
crs = 28992, agr = "constant")
# Almacenar
# save(meuse_sf, meuse_riv, meuse_grid, file = "datos/st_meuse.RData")
# Representar
plot(meuse_sf["zinc"], pch = 16, cex = 1.5, main = "",
breaks = "quantile", key.pos = 4, reset = FALSE)
plot(meuse_riv, col = "lightblue", add = TRUE)
plot(st_geometry(meuse_grid), pch = 3, cex = 0.2, col = "lightgray", add = TRUE)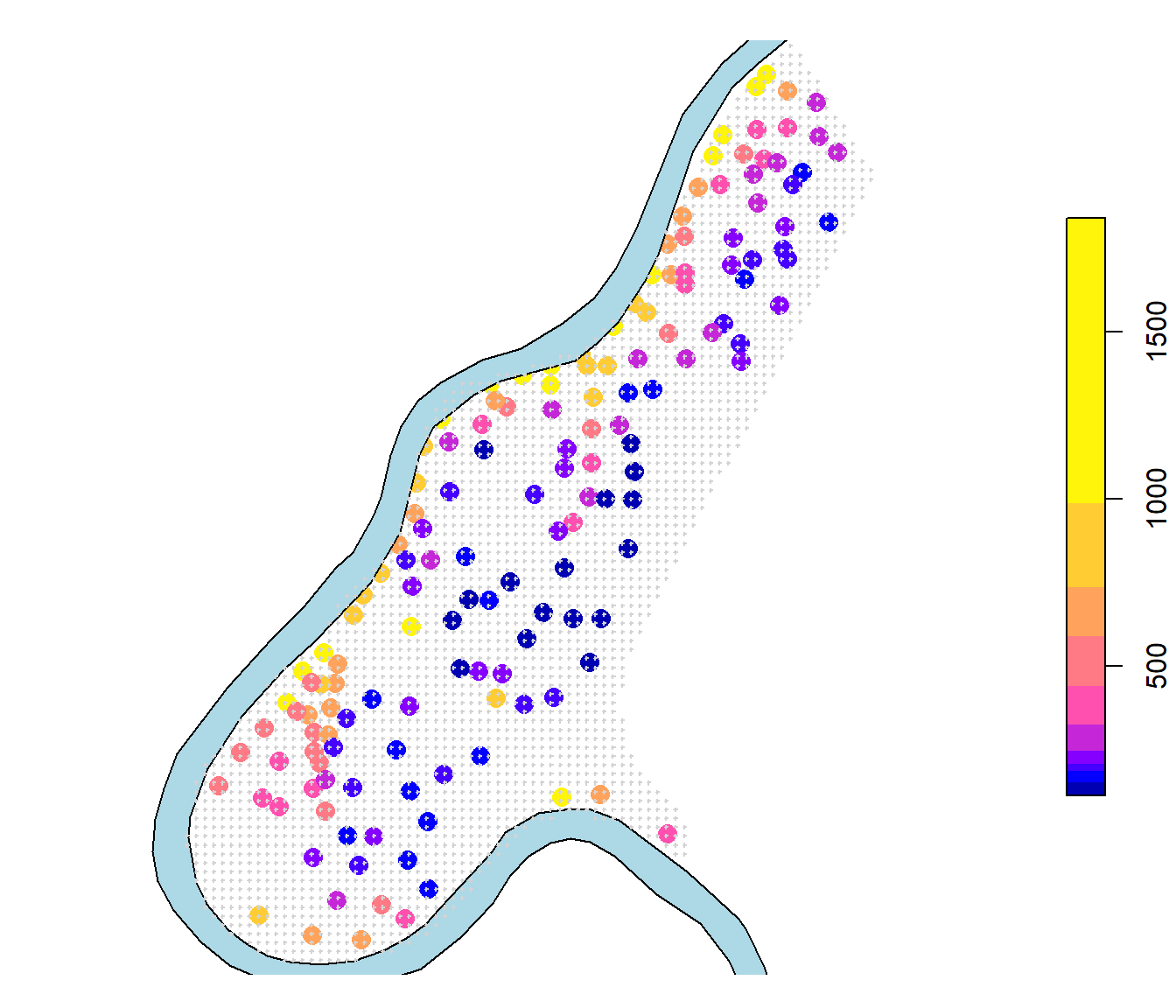
Figura 2.1: Concentración de zinc (ppm) en el entorno del río Meuse (datos sp::meuse).
Ejercicio 2.2 (Creación y representación de datos espaciales) Cargar los datos del acuífero Wolfcamp (aquifer.RData), generar el correspondiente
objeto sf y representarlo mostrando los ejes.
2.2.1 Sistemas de referencia de coordenadas
El sistema de referencia de coordenadas (CRS) especifica la correspondencia entre valores de las coordenadas y puntos concretos en la superficie de la Tierra (o del espacio), y resulta fundamental cuando se combinan datos espaciales. En general se consideran dos tipos de CRS:
Geodésico: las coordenadas en tres dimensiones (latitud, longitud y altura) se basan en un elipsoide de referencia (global o local) que sirve como aproximación del globo terrestre (se tiene en cuenta que no es una esfera perfecta e incluso que puede haber variaciones locales). Este elipsoide, junto con información adicional sobre como interpretar las coordenadas (incluyendo el orden y el origen), define el denominado datum. Normalmente se asume que las coordenadas son en la superficie terrestre y solo se consideran:
- latitud: ángulo entre el plano ecuatorial y la línea que une la posición con el centro de la Tierra. Varía desde -90 (polo sur) hasta 90 (polo norte). Un grado equivale aproximadamente a 110.6 km. Los paralelos son las líneas en la superficie terrestre correspondientes a la misma latitud (siendo el 0 el ecuador).
- longitud: ángulo (paralelo al plano ecuatorial) entre un meridiano de referencia (arco máximo que une los polos pasando por una determinado punto, normalmente el observatorio de Greenwich) y la línea que une la posición con el centro de la Tierra. Varía desde -180 (oeste) hasta 180 (este). Un grado en el ecuador equivale a aproximadamente a 111.3 km. Los meridianos son las líneas en la superficie terrestre correspondientes a la misma longitud (siendo el 0 el meridiano de Greenwich y -180 o 180 el correspondiente antimeridiano).
La rejilla correspondiente a un conjunto de paralelos y meridianos se denomina gratícula (ver
st_graticule()).Figura 2.2: Coordenadas geográficas en la superficie terrestre (Fuente Wikimedia Commons).
Uno de los CRS más empleados es el WGS84 (World Geodetic System 1984) en el que se basa el Sistema de Posicionamiento Global (GPS).
Proyectado (cartesiano): sistema (local) en dos dimensiones que facilita algún tipo de cálculo (normalmente distancias o áreas). Por ejemplo el UTM (Universal Transverse Mercator), que emplea coordenadas en metros respecto a una cuadrícula de referencia (se divide la tierra en 60 husos de longitud, numerados, y 20 bandas de latitud, etiquetadas con letras; por ejemplo Galicia se encuentra en la cuadricula 29T). Se define relacionando estas coordenadas cartesianas con coordenadas geodésicas con un determinado datum.
En sf se emplea la librería PRØJ para definir el CRS y convertir coordenadas en distintos sistemas8.
Para obtener o establecer el CRS se puede emplear la función st_crs().
Se puede especificar mediante una cadena de texto que admita GDAL (por ejemplo "WGS84", que se corresponde con el World Geodetic System 1984), que típicamente es de la forma ESTÁNDAR:CÓDIGO (también puede ser una cadena de texto PROJ.4).
El estándar más empleado es el EPSG (European Petroleum Survey Group), y es que que da por hecho el paquete sf cuando se especifica el CRS mediante un número.
También admite el estándar OGC WKT (Open Geospatial Consortium well-known text) que es el que emplea internamente, pero resulta complicado manejar en la práctica.
st_crs("WGS84")## Coordinate Reference System:
## User input: WGS84
## wkt:
## GEOGCRS["WGS 84",
## DATUM["World Geodetic System 1984",
## ELLIPSOID["WGS 84",6378137,298.257223563,
## LENGTHUNIT["metre",1]]],
## PRIMEM["Greenwich",0,
## ANGLEUNIT["degree",0.0174532925199433]],
## CS[ellipsoidal,2],
## AXIS["geodetic latitude (Lat)",north,
## ORDER[1],
## ANGLEUNIT["degree",0.0174532925199433]],
## AXIS["geodetic longitude (Lon)",east,
## ORDER[2],
## ANGLEUNIT["degree",0.0174532925199433]],
## ID["EPSG",4326]]all.equal(st_crs(4326), st_crs("EPSG:4326"), st_crs("WGS84"))## [1] TRUEst_crs(nc)## Coordinate Reference System:
## User input: NAD27
## wkt:
## GEOGCRS["NAD27",
## DATUM["North American Datum 1927",
## ELLIPSOID["Clarke 1866",6378206.4,294.978698213898,
## LENGTHUNIT["metre",1]]],
## PRIMEM["Greenwich",0,
## ANGLEUNIT["degree",0.0174532925199433]],
## CS[ellipsoidal,2],
## AXIS["latitude",north,
## ORDER[1],
## ANGLEUNIT["degree",0.0174532925199433]],
## AXIS["longitude",east,
## ORDER[2],
## ANGLEUNIT["degree",0.0174532925199433]],
## ID["EPSG",4267]]En spatialreference.org se puede obtener información detallada sobre una gran cantidad de proyecciones (y permite realizar búsquedas). También puede ser de utilidad epsg.io o este listado con detalles de los parámetros.
El CRS ideal dependerá del tipo de problema y de la zona cubierta por los datos (ver e.g Lovelace et al, 2021, Sección 6.3, para más información).
En general en estadística espacial nos interesará trabajar con coordenadas proyectadas, de forma que tenga sentido emplear la distancia euclídea (algo que puede ser poco o nada razonable si se trabaja con coordenadas geodésicas en una zona muy amplia del globo o cerca de los polos).
En el caso de coordenadas sin proyectar (latitud/longitud) puede ser preferible trabajar con distancias ortodrómicas (longitud del arco del círculo máximo que une los puntos, great circle distances)9.
Es importante destacar que cambiar el CRS no reproyecta los datos, hay que emplear st_transform() para hacerlo, como se describe en la Sección 2.4.
Finalmente hay que insistir también en que el campo de aplicación de la estadística espacial no se restringe al análisis de datos geográficos (por ejemplo nos puede interesar analizar el desgaste en la pared de un crisol empleado en fundición) y en estos casos los CRS geográficos carecen de sentido. De todos modos habrá que emplear un sistema de coordenadas que permita calcular algún tipo de salto o distancia entre puntos (aunque siempre se pueden considerar coordenadas espaciales tres dimensiones con la distancia euclídea).
2.2.2 Integración con el ecosistema tidyverse
El paquete sf es compatible con tidyverse y proporciona métodos para interactuar con los paquetes dplyr,
tidyr y ggplot2.
Algunos de los métodos de interés para manipular datos espaciales con el paquete dplyr son:
filter(),select(),mutate(),summarise(..., do_union = TRUE, is_coverage = FALSE),group_by(),ungroup(), etc.inner_join(),left_join(),right_join(),full_join(),semi_join(),anti_join(),st_join().st_drop_geometry(),st_set_crs().
Para detalles ver la referencia.
En el caso del paquete ggplot2 se puede consultar la referencia y el tutorial Drawing beautiful maps programmatically with R, sf and ggplot2:
- Part 1: Basics (General concepts illustrated with the world Map).
- Part 2: Layers (Adding additional layers: an example with points and polygons).
- Part 3: Layouts (Positioning and layout for complex maps).
Por ejemplo, se puede generar un gráfico similar al de la Figura 1.2 (porcentaje de incremento de las defunciones en el año 2020 respecto al 2019 en las CCAA españolas; datos INE), con el siguiente código:
library(dplyr)
library(tidyr)
library(sf)
library(mapSpain) # install.packages("mapSpain")
load("datos/mortalidad.RData")
mort_sf <- mortalidad %>%
filter(!ccaa.code %in% c("00", "99"), periodo %in% c("2019", "2020"), sexo == "Total") %>%
select(-sexo, -ccaa.name) %>%
pivot_wider(names_from = periodo, values_from = value, names_prefix = "mort.") %>%
mutate(incremento = 100*(mort.2020 - mort.2019)/mort.2019)
# CUIDADO: el primer elemento de xxx_join debe ser un objeto sf
# para que lo procese el paquete sf
mort_sf <- esp_get_ccaa() %>%
left_join(mort_sf, by = c("codauto" = "ccaa.code"))
library(ggplot2)
ggplot(mort_sf) +
geom_sf(aes(fill = incremento), color = "grey70") +
scale_fill_gradientn(colors = hcl.colors(10, "Blues", rev = TRUE)) +
geom_sf_label(aes(label = paste0(round(incremento, 1), "%")), alpha = 0.5) +
geom_sf(data = esp_get_can_box(), color = "grey70") +
theme_void()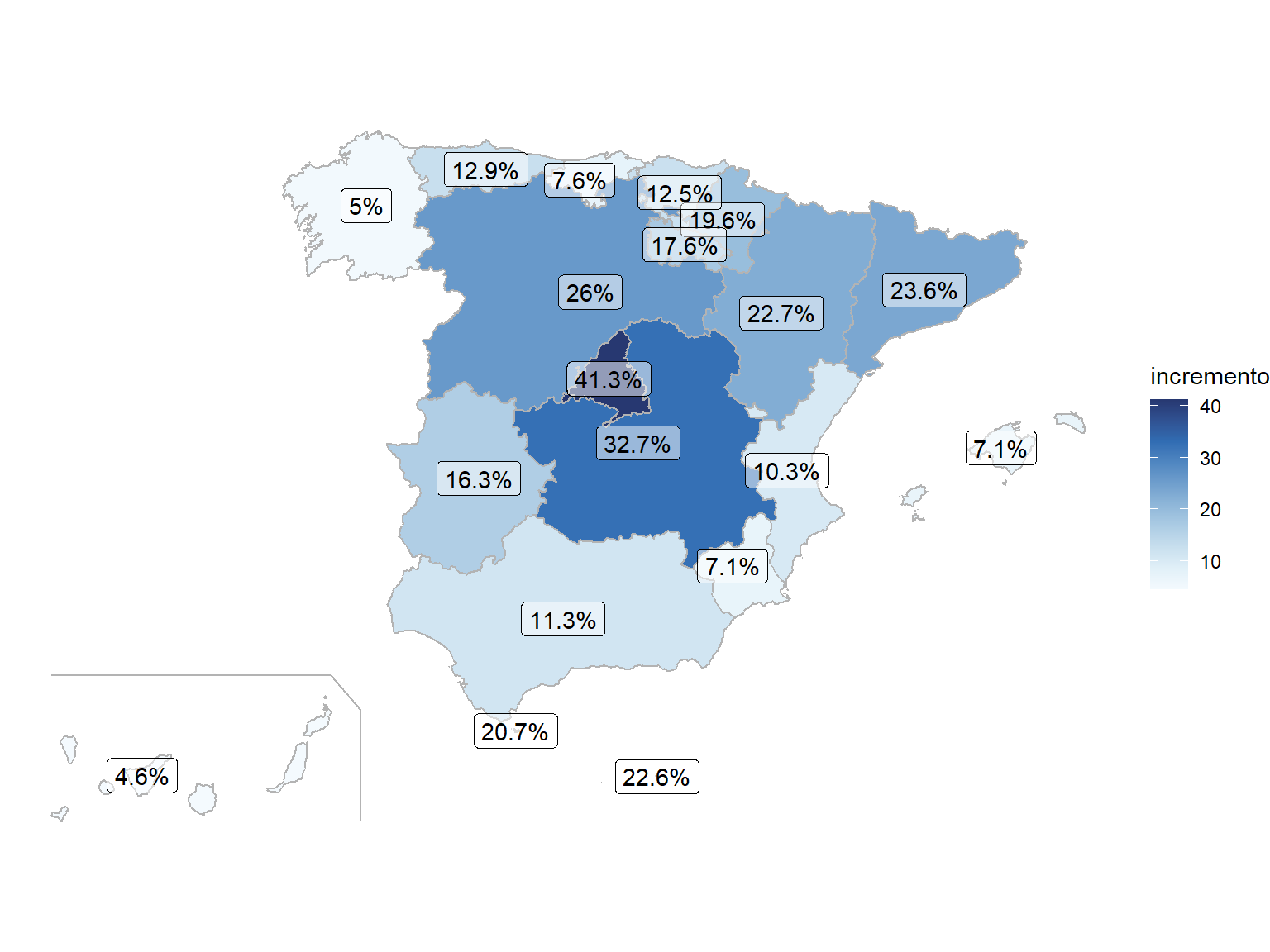
Figura 2.3: Ejemplo de gráfico generado empleando los paquetes dplyr y ggplot2.
Sin embargo, en este libro se supone que no se está familiarizado con estas herramientas y se evitará su uso (aunque pueden resultar más cómodas después de su aprendizaje).
Para una introducción a dplyr, ver por ejemplo la viñeta Introduction to dplyr,
el Capítulo 5 del libro R for Data Science o el Capítulo 4 de los apuntes Prácticas de Tecnologías de Gestión y Manipulación de Datos.
No obstante, en ciertas ocasiones emplearemos el operador pipe %>% (tubería, redirección) por comodidad.
Este operador permite canalizar la salida de una función a la entrada de otra.
Por ejemplo segundo(primero(datos)) se traduce en datos %>% primero %>% segundo
(facilitando la lectura de expresiones de izquierda a derecha).
Secuencia de puntos que forma un anillo cerrado, que no se interseca; el primero anillo definen el anillo exterior, anillos posteriores definen agujeros. Según la norma, los puntos del anillo exterior deben especificarse en sentido contrario a las agujas del reloj y los de los agujeros en sentido de las agujas del reloj.↩︎
Empleado en la viñeta del paquete
gstatcon el paquetesp.↩︎El paquete
sfadmite las últimas versiones PROJ 5 y 6, incluyendo el formato WKT-2 de 2019, mientras que el paquetespestá diseñado para cadenas de texto PROJ.4 que se recomiendan abandonar (las últimas versiones permiten añadir una cadena WKT2 comocomment).↩︎Algo que ya hace de forma automática el paquete
gstat.↩︎