1.3 Procesos espaciales estacionarios

Supongamos que $\left\{ Z(\mathbf{s}) : \mathbf{s} \in D \subset \mathbb{R}^{d} \right\}$ es un proceso geoestadístico. Este proceso aleatorio se puede caracterizar a través de las funciones de distribución finito-dimensionales: \[F_{\mathbf{s}_1, \ldots, \mathbf{s}_m}(z_1, \ldots, z_m) = P\left(Z(\mathbf{s}_1)\leq z_1 , \ldots,Z(\mathbf{s}_m)\leq z_m \right)\] (o de las funciones de densidad correspondientes $f_{\mathbf{s}_1, \ldots, \mathbf{s}_m}(z_1, \ldots, z_m)$. Por ejemplo, el proceso se dice normal (o gaussiano) si para cada posible conjunto de $m \in \mathbb{N}$ posiciones espaciales, $\{\mathbf{s}_1, \ldots, \mathbf{s}_m\}$, su función de distribución $F_{\mathbf{s}_1, \ldots, \mathbf{s}_m}$ es normal (gaussiana).

Como ya se comentó en la Sección 1.1, en general no se puede disponer de una realización completa del proceso $Z(\cdot)$ y solamente se observan valores en unas posiciones espaciales conocidas $\left\{ \mathbf{s}_1, \ldots, \mathbf{s}_{n} \right\}$ (que por lo general van a ser irregulares). Por tanto es necesario hacer algunas suposiciones acerca del proceso de forma que sea posible la inferencia sobre el mismo. Lo habitual es asumir algún tipo de estacionariedad del proceso (o del proceso de error, suponiendo que el proceso no tiene media constante y sigue el modelo general (1.1)).

El proceso $Z(\cdot)$ se dice estrictamente estacionario si al trasladar (en cualquier dirección) una configuración cualquiera de posiciones espaciales la distribución conjunta no varia: \[F_{\mathbf{s}_1 +\mathbf{h}, \ldots,\mathbf{s}_m +\mathbf{h}}(z_1, \ldots, z_m) = F_{\mathbf{s}_1, \ldots, \mathbf{s}_m}(z_1, \ldots, z_m),\ \forall \mathbf{h}\in D,\ \forall m\geq 1.\]

El proceso $Z(\cdot)$ se dice estacionario de segundo orden (también proceso estacionario homogéneo o débilmente estacionario) si tiene media constante y la covarianza entre dos posiciones depende únicamente del salto entre ellas:

$E(Z(\mathbf{s}))=\mu,\ \forall \mathbf{s}\in D$.
$Cov(Z(\mathbf{s}_1), Z(\mathbf{s}_2)) = C(\mathbf{s}_1 -\mathbf{s}_2),\ \forall \mathbf{s}_1 ,\mathbf{s}_2 \in D$.

La función $C(\cdot)$ se denomina covariograma (también autocovariograma o función de covarianzas). Si además $C(\mathbf{h}) \equiv C(\left\| \mathbf{h}\right\|)$ (sólo depende de la magnitud y no de la dirección del salto) se dice que el covariograma es isotrópico (en caso contrario se dice que es anisotrópico; Sección 3.2.2).

Si un proceso es estrictamente estacionario y $Var(Z(\mathbf{s}))$ es finita, entonces es estacionario de segundo orden. Además, como es bien conocido, en el caso de procesos normales ambas propiedades son equivalentes (ya que están caracterizados por su media y covarianza).

En algunos casos en lugar del covariograma se utiliza el correlograma: \[\rho (\mathbf{h}) = \dfrac{C(\mathbf{h})}{C(\mathbf{0})} \in \left[-1,+1\right],\] suponiendo que $C(\mathbf{0}) = Var(Z(\mathbf{s})) >0$. Sin embargo lo habitual es modelar la dependencia espacial a través del variograma (principalmente por sus ventajas en la estimación; Sección 3.1), definido a continuación.

Se dice que el proceso es intrínsecamente estacionario (también proceso espacial de incrementos estacionarios u homogéneos) si:

$E(Z(\mathbf{s}))=\mu,\ \forall \mathbf{s}\in D$.
$Var(Z(\mathbf{s}_1)-Z(\mathbf{s}_2)) = 2\gamma (\mathbf{s}_1 - \mathbf{s}_2),\ \forall \mathbf{s}_1 ,\mathbf{s}_2 \in D$.

La función $2\gamma (\cdot)$ se denomina variograma y $\gamma (\cdot)$ semivariograma. Al igual que en el caso anterior, si además $\gamma(\mathbf{h}) \equiv \gamma(\left\| \mathbf{h}\right\|)$ (sólo depende de la distancia) se dice que el variograma es isotrópico.

La clase de procesos intrínsecamente estacionarios es más general que la clase de procesos estacionarios de segundo orden. Si un proceso estacionario de segundo orden tiene covariograma $C(\cdot)$, como: \[\begin{aligned} Var(Z(\mathbf{s}_1)-Z(\mathbf{s}_2)) &= Var(Z(\mathbf{s}_1)) + Var(Z(\mathbf{s}_2))-2Cov(Z(\mathbf{s}_1),Z(\mathbf{s}_2)) \\ &=2\left(C(\mathbf{0})-C(\mathbf{s}_1 -\mathbf{s}_2)\right), \end{aligned}\] entonces su semivariograma viene dado por: \[\gamma (\mathbf{h}) = C(\mathbf{0})-C(\mathbf{h}),\] y por tanto es un proceso intrínsecamente estacionario. El reciproco en general no es cierto (por ejemplo el caso de un movimiento browniano), aunque sí se verifica en muchos casos. Normalmente cuando no se verifica es debido a que el proceso no tiene media constante y puede ser modelado como una función de tendencia más un error estacionario de segundo orden (o cuando se consideran los errores del modelo general, la tendencia no está especificada correctamente; ver Sección 3.3.2).

Si el variograma está acotado y: \[\lim \limits_{\left\| \mathbf{h}\right\| \rightarrow \infty }\gamma(\mathbf{h})=\sigma^2,\] entonces³ podemos obtener el covariograma correspondiente como: \[C(\mathbf{h})=\sigma^2-\gamma (\mathbf{h}).\] A $\sigma^{2} = C(\mathbf{0})$ se le denomina umbral (o meseta) del semivariograma. La relación entre el semivariograma y el covariograma se ilustra en la Figura 1.4.

1.3.1 Características del variograma

Además del umbral (si existe, ya que el variograma podría no estar acotado; ver sección anterior), hay otras características geométricas del variograma (o del covariograma) de especial importancia⁴, entre ellas destacarían el efecto pepita (o nugget) y el rango (o alcance). La Figura 1.4 ilustra las distintas características del semivariograma.

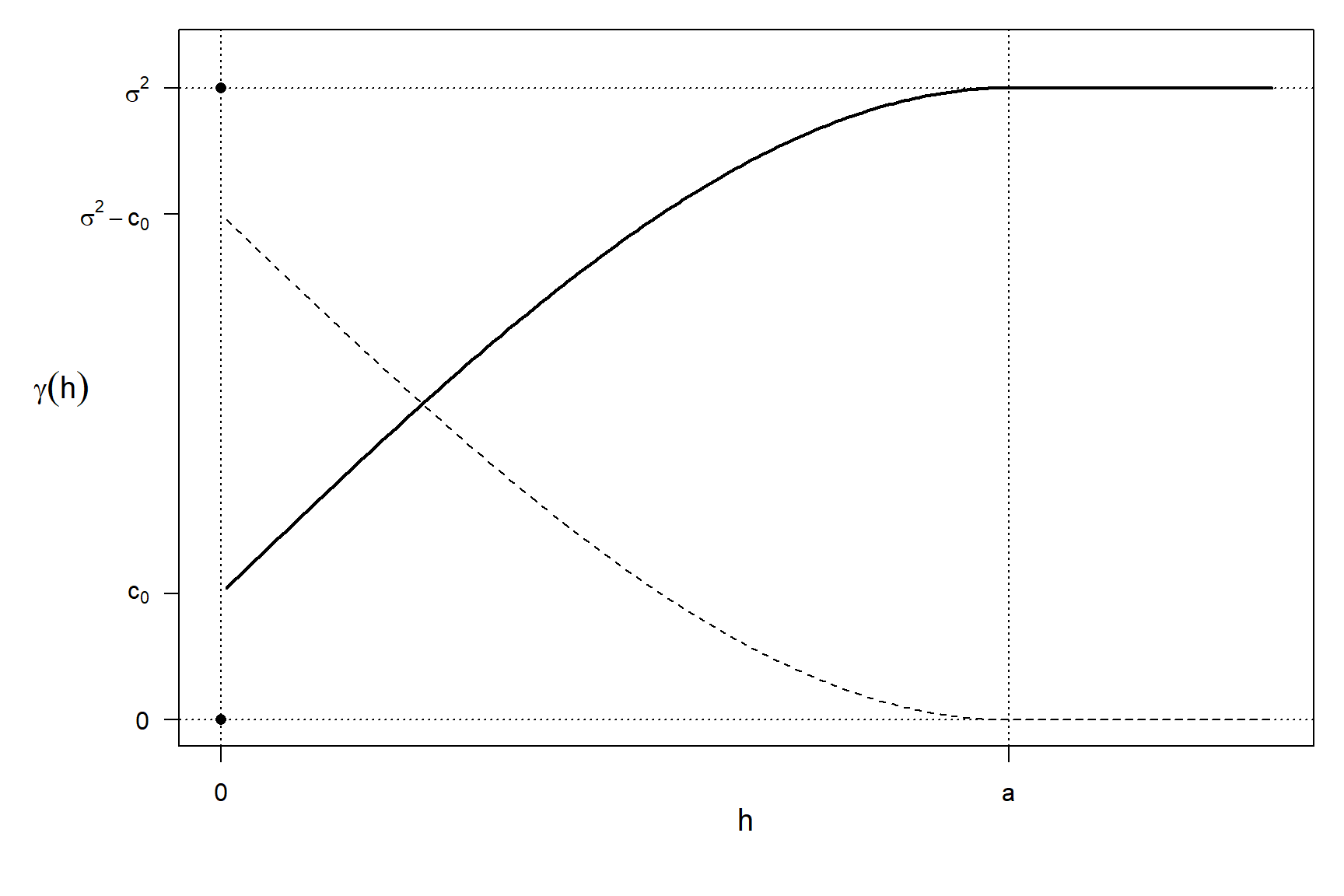
$Relación entre el covariograma (línea discontinua) y el variograma (línea continua) en el caso unidimensional (o isotrópico), y principales características: nugget ($c_0$), umbral ($\sigma^2$; umbral parcial $\sigma^2 - c_0$) y rango ($a$).$

Figura 1.4: Relación entre el covariograma (línea discontinua) y el variograma (línea continua) en el caso unidimensional (o isotrópico), y principales características: nugget ($c_0$), umbral ($\sigma^2$; umbral parcial $\sigma^2 - c_0$) y rango ($a$).

Siempre se verifica que $\gamma (\mathbf{0})=0$, sin embargo puede ser que: \[\lim \limits_{\mathbf{h}\rightarrow \mathbf{0}} \gamma(\mathbf{h}) = c_0 > 0.\] entonces $c_0$ se denomina efecto pepita (o nugget)⁵. Además, si $\sigma^{2}$ es el umbral del semivariograma (suponiendo que existe), a $\sigma ^{2} -c_0$ se le denomina umbral parcial.

Las propiedades de continuidad (y derivabilidad) del variograma (o el covariograma) en el origen están relacionadas con las propiedades de continuidad (y diferenciabilidad) en media cuadrática del proceso $Z(\cdot)$ (ver e.g. Chilès y Delfiner, 1999, Sección 2.3.1). Por ejemplo, el proceso es continuo en media cuadrática si y sólo si su variograma (covariograma) es continuo en el origen. Entonces la presencia de efecto nugget indica que (en teoría) el proceso no es continuo y por tanto altamente irregular.

La proporción del efecto nugget en el umbral total $c_0 /\sigma^{2}$ proporciona mucha información acerca del grado de dependencia espacial presente en los datos. Por ejemplo, en el caso en que toda la variabilidad es efecto nugget (i.e. $\gamma (\mathbf{h})=c_0$, $\forall \mathbf{h}\neq \mathbf{0}$) entonces $Z(\mathbf{s}_1)$ y $Z(\mathbf{s}_2)$ son incorrelados $\forall \mathbf{s}_1 ,\mathbf{s}_2 \in D$ independientemente de lo cerca que estén (el proceso $Z(\cdot)$ es ruido blanco). Por tanto podemos pensar en $c_0 /\sigma^{2}$ como la proporción de “variabilidad independiente”, aunque en la práctica típicamente no se dispone de información sobre el variograma a distancias menores de $\min \left\{ \left\| \mathbf{s}_{i} -\mathbf{s}_{j} \right\| :1\leq i<j\leq n\right\}$ (la estimación de $c_0$ se obtiene normalmente extrapolando un variograma experimental cerca del origen).

Si $\sigma ^{2}$ es el umbral del semivariograma (suponiendo que existe), se define el rango (o alcance) del semivariograma en la dirección $\mathbf{e}_0 \in \mathbb{R}^{d}$ con $\left\| \mathbf{e}_0 \right\| = 1$, como el mínimo salto en esa dirección en el que se alcanza el umbral: \[a_0 =\min \left\{ a:\gamma (a\left( 1+\varepsilon \right) \mathbf{e}_0 )=\sigma ^{2} , \forall \varepsilon >0\right\}.\] El rango en la dirección $\mathbf{e}_0$ puede interpretarse como el salto $h$ a partir del cual no hay correlación entre $Z(\mathbf{s})$ y $Z(\mathbf{s}\pm h\mathbf{e}_0)$, por tanto está íntimamente ligado a la noción de “zona de influencia” (y tiene un papel importante en la determinación de criterios de vecindad). En los casos en los que el semivariograma alcanza el umbral asintóticamente (rango infinito), se suele considerar el rango práctico, definido como el mínimo salto en el que se alcanza el 95% del umbral parcial.

El variograma y el covariograma son las funciones habitualmente consideradas en geoestadística para el modelado de la dependencia espacial (o espacio-temporal), y son consideradas como un parámetro (de especial interés) del proceso. En la práctica normalmente se suele utilizar el variograma, no sólo porque es más general (puede existir en casos en que el covariograma no), sino por las ventajas en su estimación (Sección 3.1; Cressie, 1993, Sección 2.4.1). No obstante, en muchos casos los modelos de variograma se obtienen a partir de modelos de covariograma.

1.3.2 Propiedades elementales del covariograma y del variograma

El variograma y el covariograma deben verificar ciertas propiedades que sus estimadores no siempre verifican, a continuación se detallan algunas de ellas.

Si $Z(\cdot)$ es un proceso estacionario de segundo orden con covariograma $C(\cdot)$, entonces se verifica que $C(\mathbf{0}) = Var( Z(\mathbf{s}) ) \geq 0$, es una función par $C(\mathbf{h})=C(-\mathbf{h})$, y por la desigualdad de Cauchy-Schwarz $\left| C(\mathbf{h})\right| \leq C(\mathbf{0})$. Además, el covariograma debe ser semidefinido positivo, es decir: \[\sum\limits_{i=1}^{m} \sum\limits_{j=1}^{m} a_i a_j C(\mathbf{s}_i-\mathbf{s}_j) \geq 0 \\ \forall m\geq 1,\ \forall \mathbf{s}_i \in D,\ \forall a_i \in \mathbb{R};\ i=1, \ldots,m,\] ya que: \[\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{m}a_i a_j C(\mathbf{s}_i -\mathbf{s}_j) = Var\left\{\sum\limits_{i=1}^{m}a_i Z(\mathbf{s}_i) \right\}\] La condición es necesaria y suficiente para que exista un proceso estacionario de segundo orden con covariograma $C(\cdot)$ (se puede construir un proceso normal multivariante con covarianzas definidas por $C(\cdot)$). Por tanto la clase de covariogramas válidos en $\mathbb{R}^d$ es equivalente a la clase de funciones semidefinidas positivas en $\mathbb{R}^d$.

Algunas propiedades adicionales que verifican los covariogramas son las siguientes:

Si $C(\cdot)$ es un covariograma válido en $\mathbb{R}^d$, entonces $aC(\cdot)$, $\forall a\geq 0$, es también un covariograma válido en $\mathbb{R}^d$.
Si $C_1 (\cdot)$ y $C_2 (\cdot)$ son covariogramas válidos en $\mathbb{R}^d$, entonces $C_1 (\cdot) + C_2 (\cdot)$ es un covariograma válido en $\mathbb{R}^d$. Lo que equivale a suponer que el proceso $Z(\cdot)$ se obtiene como suma de dos procesos estacionarios de segundo orden independientes: $Z(\mathbf{s})=Z_1 (\mathbf{s}) + Z_2 (\mathbf{s})$, con covariogramas $C_1 (\cdot)$ y $C_2 (\cdot)$ respectivamente.
Si $C_1 (\cdot)$ y $C_2 (\cdot)$ son covariogramas válidos en $\mathbb{R}^d$, entonces $C(\cdot) = C_1 (\cdot)C_2 (\cdot)$ es un covariograma válido en $\mathbb{R}^d$. Lo que equivale a suponer que el proceso se obtiene como producto de dos procesos estacionarios de segundo orden independientes.
Un covariograma isotrópico válido en $\mathbb{R}^d$ es también un covariograma isotrópico válido en $\mathbb{R}^m$, $\forall m\leq d$ (el recíproco no es en general cierto, ver e.g. Cressie, 1993, p. 84).

Si $\gamma (\cdot)$ es el semivariograma de un proceso intrínsecamente estacionario $Z(\cdot)$, entonces se verifica que $\gamma (\mathbf{0})=0$, $\gamma (\mathbf{h})\geq 0$ y $\gamma (\mathbf{h})=\gamma (-\mathbf{h})$. El semivariograma debe ser además condicionalmente semidefinido negativo, es decir: \[\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{m}a_i a_j \gamma(\mathbf{s}_i -\mathbf{s}_j) \leq 0 \\ \forall m\geq 1,\forall \mathbf{s}_i \in D,\forall a_i \in \mathbb{R};i=1, \ldots,m,\text{tales que } \sum\limits_{i=1}^{m}a_i = 0.\] Esta condición es necesaria pero no suficiente (aunque pocas condiciones adicionales son necesarias para que el recíproco sea cierto; ver Cressie, 1993, Sección 3.5.2).

Algunas propiedades adicionales que verifica un variograma son las siguientes:

Si $\gamma (\cdot)$ es un semivariograma válido en $\mathbb{R}^d$, entonces $a\gamma (\cdot)$, $\forall a\geq 0$, es también un semivariograma válido en $\mathbb{R}^d$.
Si $\gamma_1 (\cdot)$ y $\gamma_2 (\cdot)$ son semivariogramas válidos en $\mathbb{R}^d$, entonces $\gamma_1 (\cdot)+\gamma_2 (\cdot)$, es también un semivariograma válido en $\mathbb{R}^d$. Lo que equivale a suponer que el proceso $Z(\cdot)$ se obtiene como suma de dos procesos intrínsecamente estacionarios independientes: $Z(\mathbf{s})=Z_1 (\mathbf{s})+Z_2 (\mathbf{s})$, con semivariogramas $\gamma_1 (\cdot)$ y $\gamma_2 (\cdot)$ respectivamente.
Un variograma isotrópico válido en $\mathbb{R}^d$ es también un variograma isotrópico válido en $\mathbb{R}^m$, $\forall m\leq d$.

Se suelen emplear estas propiedades para la obtención de modelos de variograma válidos, como por ejemplo en el caso de la anisotropía zonal (Sección 3.2.2) o del modelo lineal de (co)regionalización (secciones 3.2.3 y 5.X).

1.3.3 Procesos agregados

En algunos casos los datos pueden ser agregaciones espaciales en lugar de observaciones puntuales (e incluso observaciones sobre distintos soportes) o, por ejemplo, puede ser de interés la estimación de medias espaciales a partir de datos puntuales. Estas agregaciones pueden ser modeladas como el promedio de un proceso puntual, lo que permite deducir fácilmente las relaciones entre covariogramas y variogramas vinculados a diferentes soportes.

Supongamos que el proceso espacial $Z(\cdot)$ definido sobre $D\subset \mathbb{R} ^{d}$ es integrable en media cuadrática. Entonces, si $B\subset D$ es un subconjunto acotado e integrable con $\left| B\right| =\int_B d\mathbf{s} > 0$, se puede definir el proceso espacial agregado (también se denomina regularizado) como: \[Z(B)\equiv \dfrac{1}{\left| B\right| } \int_{B}Z(\mathbf{s})d\mathbf{s}.\]

Si por ejemplo el proceso puntual es intrínsecamente estacionario con semivariograma $\gamma (\cdot)$, entonces a partir del variograma puntual podemos obtener el variograma del proceso agregado:

\[\begin{aligned} Var\left( Z(B_1)-Z(B_2)\right) = & -\dfrac{1}{\left| B_1 \right| ^{2} } \int_{B_1 }\int_{B_1 }\gamma(\mathbf{s}-\mathbf{u})d\mathbf{s}d\mathbf{u} \\ & -\dfrac{1}{\left| B_2 \right|^{2} } \int_{B_2}\int_{B_2}\gamma(\mathbf{s}-\mathbf{u})d\mathbf{s}d\mathbf{u} \\ & +\dfrac{1}{\left| B_1 \right| \left| B_2 \right| } \int_{B_1 }\int_{B_2} 2\gamma(\mathbf{s}-\mathbf{u})d\mathbf{s}d\mathbf{u}. \end{aligned}\]

Aunque nos centraremos principalmente en el caso de soporte puntual, los métodos descritos en este libro pueden ser extendidos para el caso de distintos soportes (por ejemplo el block kriging descrito en la Sección 4.7.1). Sin embargo, en la práctica pueden aparecer dificultades, especialmente al combinar observaciones en distintos soportes (esto es lo que se conoce como el problema de cambio de soporte, o el modifiable areal unit problem, MAUP). Para más detalles ver por ejemplo Cressie (1993, Sección 5.2) ó Chilès y Delfiner (1999, Sección 2.4).

Suponiendo que $\lim \limits_{\left\| \mathbf{h}\right\| \rightarrow \infty } C(\mathbf{h})=0$.↩︎
Además de poder interpretar su influencia en la predicción espacial (Sección 4.5.2), son utilizadas en la parametrización de la mayoría de los modelos de variogramas o covariogramas (Sección 3.2.1).↩︎
El origen de esta denominación esta relacionado con la terminología minera. En algunos yacimientos de metal, como por ejemplo en el caso del oro, el mineral suele obtenerse como pepitas de material puro y estas pepitas normalmente son más pequeñas que el tamaño de la unidad de muestreo (lo que produce una variabilidad adicional en la muestra).↩︎