1.3 Cálculo de la distribución Bootstrap: exacta y aproximada
1.3.1 Distribución bootstrap exacta
En principio siempre es posible calcular la distribución en el remuestreo del estadístico bootstrap de forma exacta. Al menos para el bootstrap uniforme, que es el más habitual. El motivo es que la distribución de probabilidad de la que se remuestrea en el universo bootstrap es discreta y con un número finito de valores: \(X_1,\ldots ,X_n\). Así pues, cada observación bootstrap, \(X_i^{\ast}\), ha de tomar necesariamente alguno de esos \(n\) valores y, por tanto, el número de posibles remuestras, \(\mathbf{X}^{\ast}=\left( X_1^{\ast },\ldots ,X_n^{\ast} \right)\), obtenibles mediante el bootstrap uniforme es finito, concretamente \(n^{n}\). Aún siendo finito, este número es gigantescamente grande incluso para tamaños muestrales pequeños (salvo casos extremos del tipo \(n=2,\ldots ,9\)). Por ejemplo, para \(n=10\), tenemos \(10^{10}\) (diez mil millones de) posibles remuestras bootstrap y para \(n=20\), tendríamos \(20^{20}\simeq 10.4857\cdot 10^{25}\) (algo más de cien cuatrillones). Incluso para estos tamaños muestrales el problema de cálculo de la distribución bootstrap exacta de \(\mathbf{X}^{\ast}\) es inabordable.
1.3.2 Vectores de remuestreo
Una forma alternativa de representar las posibles remuestras bootstrap es mediante los llamados vectores de remuestreo. Son utilizables en el caso de que el estadístico de interés sea funcional, es decir, cuando \(R\) depende de la muestra sólo a través de la distribución empírica o, lo que es lo mismo, el valor de \(R\) no cambia cuando realizamos una permutación arbitraria sobre los elementos de la muestra (los cambiamos de orden). Consideremos la remuestra bootstrap \(\mathbf{X}^{\ast} =\left( X_1^{\ast},\ldots ,X_n^{\ast} \right)\) y denotemos por \[N_j=\#\left\{ i\in \left\{ 1,\ldots ,n\right\} : X_i^{\ast}=X_j\right\}.\] Obviamente, si el orden en el que se han obtenido los elementos de la muestra no es importante, entonces el vector \(\mathbf{N}=\left( N_1,\ldots ,N_n \right)\) contiene la misma información que la remuestra bootstrap \(\mathbf{X}^{\ast}\). Esencialmente lo que hace el vector \(\mathbf{N}\) es contabilizar cuantas veces se repite cada elemento de la muestra original en la remuestra bootstrap. Con esta notación, el vector de remuestreo bootstrap, \(\mathbf{P}^{\ast}=\left( P_1^{\ast},\ldots ,P_n^{\ast} \right)\), se define como \(P_i^{\ast}=\frac{N_i}{n}\), \(i=1,\ldots ,n\).
La distribución en el remuestreo de \(\mathbf{N}\), bajo el bootstrap uniforme, es multinomial: \(\mathbf{N}\sim \mathcal{M}_n\left( n,\left( \frac{1}{n},\ldots ,\frac{1}{n} \right) \right)\). Así que su masa de probabilidad, y por tanto la de \(\mathbf{P}^{\ast}\), es fácilmente calculable: \[\begin{aligned} P\left( N_1=m_1,\ldots ,N_n=m_n \right) &= \frac{n!}{m_1!\cdots m_n!}\left( \frac{1}{n} \right)^{m_1}\cdots \left( \frac{1}{n} \right) ^{m_n} \\ &= \frac{n!}{m_1!\cdots m_n!n^{n}}\text{, } \\ \end{aligned}\] para \(m_1,\ldots ,m_n\) enteros con \(\sum_{i=1}^{n}m_i = n\), donde el número de átomos de probabilidad de \(\mathbf{N}\) es ahora \(\binom{n+n-1}{n}=\binom{2n-1}{n}\).
En general \(\binom{2n-1}{n}<n^{n}\), pues el hecho de que no importe el orden de las componentes de las remuestras bootstrap provoca un menor número de átomos de probabilidad. Aún así dicho cardinal es prohibitivamente grande incluso para tamaños muestrales pequeños: para \(n=10\), resultaría abordable pues \(\binom{19}{10}= 92\,378\), pero para \(n=20\) tendríamos \(\binom{39}{20}= 68\, 923\,264\,410\). De toda esa enorme cantidad de átomos, el de más grande probabilidad resulta tener una probabilidad de \(\frac{n!}{n^{n}}\), que es insignificantemente pequeña para tamaños pequeños como \(n=20\), con \(\frac{20!}{20^{20}}\sim 2.\, 320\,2\times 10^{-8}\). De todas formas, existen raras ocasiones en las que el número de átomos de probabilidad de \(R^{\ast}\) resulta ser mucho menor que el de \(\mathbf{P}^{\ast}\).
Para tamaños muestrales realmente pequeños es posible encontrar todos los átomos de probabilidad de la distribución bootstrap. Un ejemplo es la media muestral con, por ejemplo, \(n=3\).
Ejemplo 1.4 (Media muestral para una muestra de tamaño 3)
Consideremos una muestra aleatoria simple de tamaño \(n=3\) de una población con distribución \(F\) y tomemos como parámetro de interés la media poblacional \(\theta \left( F \right) =\mu =\int xdF\left( x \right)\). Tomemos como estadístico de interés \(R=R\left( \mathbf{X},F \right) =\bar{X}\). El análogo bootstrap de esta estadístico es \(R^{\ast}=R\left( \mathbf{X}^{\ast},F_n \right) =\bar{X}^{\ast}\), cuya distribución en el remuestreo se puede calcular de forma exacta debido al reducido número de átomos de probabilidad que tiene. Esta es una distribución discreta con 10 posibles valores, cuyo valor más probable es precisamente \(\bar{X}\) que tiene una probabilidad bootstrap de \(\frac{2}{9}\), como puede verse en la siguiente tabla.
| \(\mathbf{X}^{\ast}\) (salvo permutaciones) | \(\mathbf{N}\) = \(\left( m_1,m_2,m_3 \right)\) | \(\mathbf{P}^{\ast}\) = \(\left(p_1,p_2,p_3 \right)\) | \(\frac{3!}{m_1!m_2!m_3!3^{3}}\) | \(\bar{X}^{\ast}\) |
|---|---|---|---|---|
| \(\left( X_1,X_1,X_1 \right)\) | \(\left( 3,0,0 \right)\) | \(\left(1,0,0 \right)\) | \(\frac{1}{27}\) | \(X_1\) |
| \(\left( X_2,X_2,X_2 \right)\) | \(\left( 0,3,0 \right)\) | \(\left(0,1,0 \right)\) | \(\frac{1}{27}\) | \(X_2\) |
| \(\left( X_3,X_3,X_3 \right)\) | \(\left( 0,0,3 \right)\) | \(\left(0,0,1 \right)\) | \(\frac{1}{27}\) | \(X_3\) |
| \(\left( X_1,X_1,X_2 \right)\) | \(\left( 2,1,0 \right)\) | \(\left( \frac{2}{3},\frac{1}{3},0 \right)\) | \(\frac{1}{9}\) | \(\frac{2X_1+X_2}{3}\) |
| \(\left( X_1,X_1,X_3 \right)\) | \(\left( 2,0,1 \right)\) | \(\left( \frac{2}{3},0,\frac{1}{3} \right)\) | \(\frac{1}{9}\) | \(\frac{2X_1+X_3}{3}\) |
| \(\left( X_1,X_2,X_2 \right)\) | \(\left( 1,2,0 \right)\) | \(\left( \frac{1}{3},\frac{2}{3},0 \right)\) | \(\frac{1}{9}\) | \(\frac{X_1+2X_2}{3}\) |
| \(\left( X_2,X_2,X_3 \right)\) | \(\left( 0,2,1 \right)\) | \(\left( 0,\frac{2}{3},\frac{1}{3} \right)\) | \(\frac{1}{9}\) | \(\frac{2X_2+X_3}{3}\) |
| \(\left( X_1,X_3,X_3 \right)\) | \(\left( 1,0,2 \right)\) | \(\left( \frac{1}{3},0,\frac{2}{3} \right)\) | \(\frac{1}{9}\) | \(\frac{X_1+2X_3}{3}\) |
| \(\left( X_2,X_3,X_3 \right)\) | \(\left( 0,1,2 \right)\) | \(\left( 0,\frac{1}{3},\frac{2}{3} \right)\) | \(\frac{1}{9}\) | \(\frac{X_2+2X_3}{3}\) |
| \(\left( X_1,X_2,X_3 \right)\) | \(\left( 1,1,1 \right)\) | \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3} \right)\) | \(\frac{2}{9}\) | \(\frac{X_1+X_2+X_3}{3}\) |
En algunas ocasiones es factible encontrar expresiones cerradas para la distribución de \(R^{\ast}\), más allá de las obvias que consisten en enumerar el ingente número de átomos de probabilidad de \(\mathbf{P}^{\ast}\): \[P^{\ast}\left( R^{\ast}=R\left( \left( m_1,\ldots ,m_n \right) ,F_n \right) \right)\] Veamos un ejemplo.
1.3.3 Inferencia sobre la mediana
En el caso de la mediana, consideremos, por simplicidad el caso de tamaño muestral impar, \(n=2m-1\). Supongamos también que no hay empates en los valores de la muestra (si los hubiese las expresiones serían más farragosas pero también calculables). La versión bootstrap del estadístico sobre el cual pivota la inferencia es \(R^{\ast}=X_{\left( m \right)}^{\ast}-X_{(m)}\). Su distribución bootstrap podría calcularse si se obtuviese la de \(X_{(m)}^{\ast}\). Pero ésta es factible de calcular por los pocos posibles valores que puede tomar el estadístico \(X_{(m)}^{\ast}\) (tan sólo los valores de la muestra original) y por la sencillez del bootstrap uniforme. Veámoslo: \[P^{\ast}\left( X_{(m)}^{\ast}>X_{(j)} \right) =P^{\ast}\left( \#\left\{ X_i^{\ast}\leq X_{(j)}\right\} \leq m-1 \right),\] pero \[\#\left\{ X_i^{\ast}\leq X_{(j)}\right\} \sim \mathcal{B}\left( n,\frac{j}{n} \right),\] con lo cual \[P^{\ast}\left( X_{(m)}^{\ast}>X_{(j)} \right) =\sum_{k=0}^{m-1}\binom{n}{k}\left( \frac{j}{n} \right)^{k} \left( \frac{n-j}{n} \right)^{n-k}\] y, por lo tanto, si \(j\geq 2\), \[\begin{aligned} P^{\ast}\left( X_{(m)}^{\ast}=X_{(j)} \right) =&\ P^{\ast}\left( X_{(m)}^{\ast}>X_{\left( j-1 \right)} \right) -P^{\ast}\left( X_{(m)}^{\ast}>X_{(j)} \right) \\ =&\ \sum_{k=0}^{m-1}\binom{n}{k}\left( \frac{j-1}{n} \right)^{k}\left( \frac{ n-j+1}{n} \right)^{n-k} \\ &-\sum_{k=0}^{m-1}\binom{n}{k}\left( \frac{j}{n} \right)^{k}\left( \frac{n-j}{ n} \right)^{n-k} \\ =&\ \sum_{k=0}^{m-1}\binom{n}{k}\left[ \left( \frac{j-1}{n} \right)^{k}\left( \frac{n-j+1}{n} \right)^{n-k}-\left( \frac{j}{n} \right)^{k}\left( \frac{n-j }{n} \right)^{n-k}\right] . \end{aligned}\]
Cuando \(j=1\), entonces \[\begin{aligned} P^{\ast}\left( X_{(m)}^{\ast} = X_{(1)} \right) &= 1-P^{\ast}\left( X_{(m)}^{\ast}>X_{(1)} \right) \\ &= 1-\sum_{k=0}^{m-1}\binom{n}{k}\left( \frac{1}{n} \right)^{k} \left( \frac{n-1}{n} \right)^{n-k}. \end{aligned}\]
1.3.4 Distribución Bootstrap aproximada por Monte Carlo
Como ya se comentó anteriormente, al conocer el mecanismo que genera los datos en el bootstrap, siempre se podrá simular dicho mecanismo mediante el método de Monte Carlo. Por lo que el algoritmo general para la aproximación de Monte Carlo del bootstrap uniforme es:
Para cada \(i=1,\ldots ,n\) arrojar \(X_i^{\ast}\) a partir de \(F_n\)
Obtener \(\mathbf{X}^{\ast}=\left( X_1^{\ast},\ldots ,X_n^{\ast} \right)\)
Calcular \(R^{\ast}=R\left( \mathbf{X}^{\ast},F_n \right)\)
Repetir \(B\) veces los pasos 1-3 para obtener las réplicas bootstrap \(R^{\ast (1)}\), \(\ldots\), \(R^{\ast (B)}\)
Utilizar esas réplicas bootstrap para aproximar la distribución en el muestreo de \(R\)
Como se mostró en la Sección 1.1.3, el paso 1 se puede llevar a cabo simulando una distribución uniforme discreta mediante el método de la transformación cuantil:
- Para cada \(i=1,\ldots ,n\) arrojar \(U_i\sim \mathcal{U}\left( 0,1 \right)\) y hacer \(X_i^{\ast}=X_{\left\lfloor nU_i\right\rfloor +1}\)
Aunque en R se recomienda emplear la función sample.
Ejemplo 1.5 (Inferencia sobre la media con varianza desconocida)
Tenemos pues \(\mathbf{X}=\left( X_1,\ldots ,X_n \right) \sim F\,\), con \(\mu\) y \(\sigma\) desconocidas
El parámetro de interés es \[\theta \left( F \right) =\mu =\int x~dF\left( x \right)\] que se estima mediante \[\theta \left( F_n \right) =\int x~dF_n\left( x \right) =\bar{X}.\] Así pues, el estadístico en el que basar la inferencia es \[R=R\left( \mathbf{X},F \right) =\sqrt{n}\frac{\bar{X}-\mu }{S_{n-1}},\] donde \(S_{n-1}^2\) es la cuasivarianza muestral: \[S_{n-1}^2=\frac{1}{n-1}\sum_{j=1}^{n}\left( X_j-\bar{X} \right)^2.\]
Bajo normalidad \(\left( X\sim \mathcal{N}\left( \mu ,\sigma^2 \right) \right)\), se sabe que \(R\sim t_{n-1}\) y, en particular, \(R\overset{d}{\rightarrow } \mathcal{N}\left( 0,1 \right)\) cuando \(n\rightarrow \infty\). Si \(F\) no es normal entonces la distribución de \(R\) ya no es una \(t_{n-1}\), pero también es cierto que, bajo ciertas condiciones, \(R\overset{d}{\rightarrow}\mathcal{N}\left(0,1 \right)\).
En el contexto bootstrap elegimos \(\hat{F}=F_n\,\), con lo cual se trata de un bootstrap naïve o uniforme. El análogo bootstrap del estadístico \(R\) será \[R^{\ast}=R\left( \mathbf{X}^{\ast},F_n \right) =\sqrt{n}\frac{ \bar{X}^{\ast}-\bar{X}}{S_{n-1}^{\ast}},\] siendo \[\begin{aligned} \bar{X}^{\ast} &= \frac{1}{n}\sum_{i=1}^{n}X_i^{\ast}, \\ S_{n-1}^{\ast 2} &= \frac{1}{n-1}\sum_{i=1}^{n}\left( X_i^{\ast}- \bar{X}^{\ast} \right)^2. \end{aligned}\]
El algoritmo bootstrap (aproximado por Monte Carlo) procedería así:
Para cada \(i=1,\ldots ,n\) arrojar \(U_i\sim \mathcal{U}\left( 0,1 \right)\) y hacer \(X_i^{\ast}=X_{\left\lfloor nU_i\right\rfloor +1}\)
Obtener \(\bar{X}^{\ast}\) y \(S_{n-1}^{\ast 2}\)
Calcular \(R^{\ast}=\sqrt{n}\frac{\bar{X}^{\ast}-\bar{X}}{ S_{n-1}^{\ast}}\)
Repetir \(B\) veces los pasos 1-3 para obtener las réplicas bootstrap \(R^{\ast (1)}, \ldots, R^{\ast (B)}\)
Aproximar la distribución en el muestreo de \(R\) mediante la distribución empírica de \(R^{\ast (1)}, \ldots, R^{\ast (B)}\)
El código para implementar este método es similar al del caso de varianza conocida del Ejemplo 1.1:
muestra <- c(0.143, 0.182, 0.256, 0.26, 0.27, 0.437, 0.509,
0.611, 0.712, 1.04, 1.09, 1.15, 1.46, 1.88, 2.08)
n <- length(muestra)
alfa <- 0.05
x_barra <- mean(muestra)
cuasi_dt <- sd(muestra)
# Remuestreo
set.seed(1)
B <- 1000
remuestra <- numeric(n)
estadistico_boot <- numeric(B)
for (k in 1:B) {
remuestra <- sample(muestra, n, replace = TRUE)
x_barra_boot <- mean(remuestra)
cuasi_dt_boot <- sd(remuestra)
estadistico_boot[k] <- sqrt(n) * (x_barra_boot - x_barra)/cuasi_dt_boot
}
# Aproximación bootstrap de los ptos críticos
pto_crit <- quantile(estadistico_boot, c(alfa/2, 1 - alfa/2))
# Construcción del IC
ic_inf_boot <- x_barra - pto_crit[2] * cuasi_dt/sqrt(n)
ic_sup_boot <- x_barra - pto_crit[1] * cuasi_dt/sqrt(n)
IC_boot <- c(ic_inf_boot, ic_sup_boot)
names(IC_boot) <- paste0(100*c(alfa/2, 1-alfa/2), "%")
IC_boot## 2.5% 97.5%
## 0.5030131 1.2888063Este procedimiento para la construcción de intervalos de confianza se denomina método percentil-t y se tratará en la Sección 4.3.
Como ejemplo adicional podemos comparar la aproximación de la distribución bootstrap del estadístico con la aproximación \(t_{n-1}\) basada en normalidad.
hist(estadistico_boot, freq = FALSE, ylim = c(0, 0.4))
abline(v = pto_crit)
curve(dt(x, n-1), add=TRUE, lty = 2)
pto_crit_t <- qt(1 - alfa/2, n-1)
abline(v = c(-pto_crit_t, pto_crit_t), lty = 2)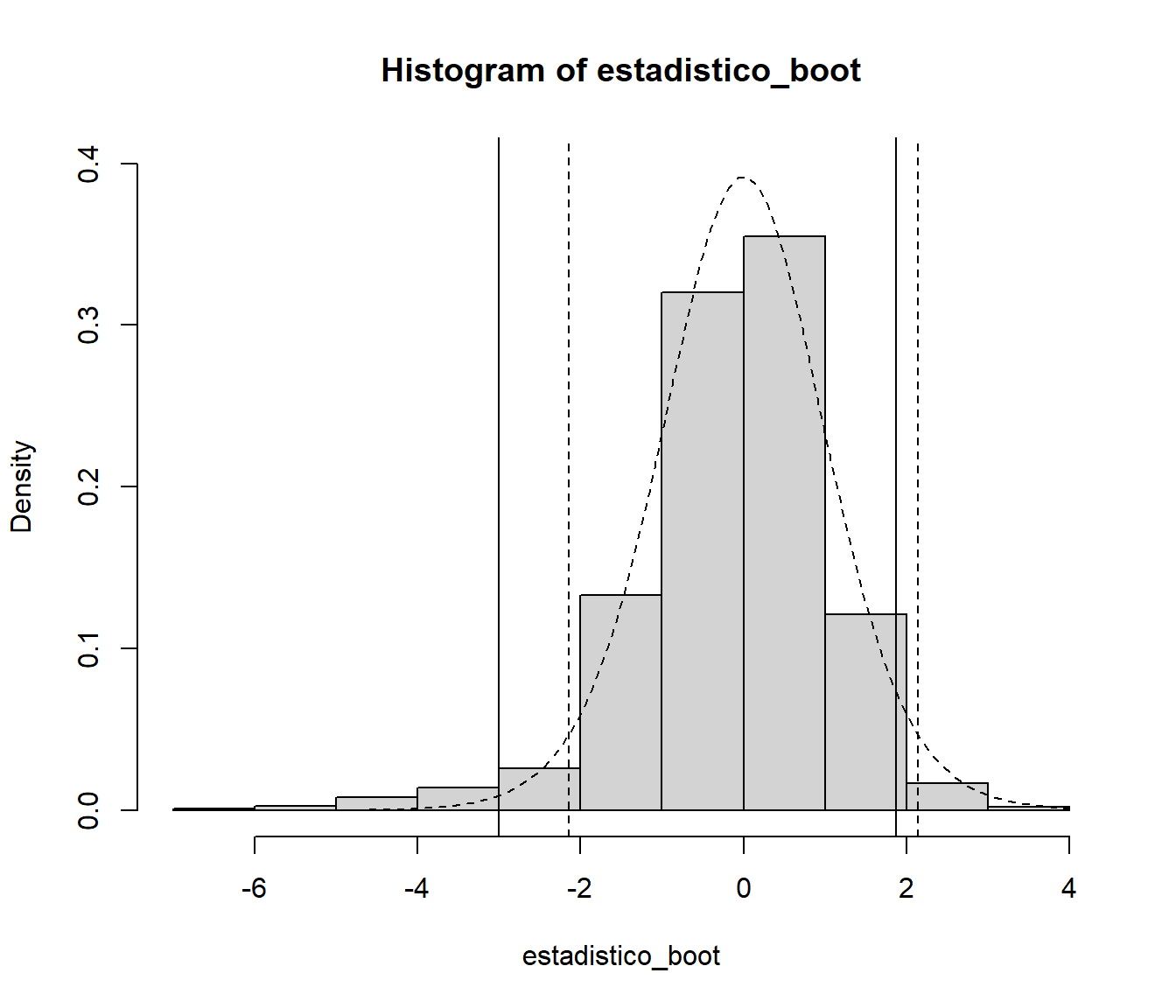
En este caso la distribución bootstrap del estadístico es más asimétrica, lo que se traducirá en diferencias entre las estimaciones por intervalos de confianza.
Por ejemplo, podemos obtener la estimación basada en normalidad mediante la función t.test():
t.test(muestra)$conf.int## [1] 0.4599374 1.1507292
## attr(,"conf.level")
## [1] 0.951.3.5 Elección del número de réplicas Monte Carlo
Normalmente el valor de \(B\) se toma del orden de varias centenas o incluso millares. En los casos en los que el bootstrap se utiliza para estimar el sesgo o la varianza de un estimador, bastará tomar un número, \(B\), de réplicas bootstrap del orden de \(B = 100, 200, 500\). Sin embargo, cuando se trata de utilizar el bootstrap para realizar contrastes de hipótesis o construir intervalos de confianza son necesarios valores mayores, del tipo \(B = 500, 1000, 2000, 5000\).
Evidentemente, la función de distribución del estadístico de interés, \(\psi \left( u \right) =P\left( R\leq u \right)\), se estimaría mediante la distribución empírica de las \(B\) realizaciones de la aproximación de Monte Carlo, \[\hat{\psi}_{B}\left( u \right) = \frac{1}{B}\sum_{i=1}^{B}\mathbf{1}\left\{ R^{\ast (i)}\leq u\right\},\] de la verdadera distribución bootstrap exacta: \(\hat{\psi}\left(u \right) =P^{\ast}\left( R^{\ast}\leq u \right)\). El error de MonteCarlo de \(\hat{\psi}_{B}\left( u \right)\) con respecto a \(\hat{\psi}\left( u \right)\) viene dado por su varianza Monte Carlo, pues su sesgo Monte Carlo es cero:
\[\begin{aligned} E^{MC}\left( \hat{\psi}_{B}\left( u \right) \right) &= \frac{1}{B} \sum_{i=1}^{B}E^{MC}\left( \mathbf{1}\left\{ R^{\ast (i)}\leq u\right\} \right) =\frac{1}{B}\sum_{i=1}^{B}P^{\ast}\left( R^{\ast \left( i \right)}\leq u \right) \\ &= \frac{1}{B}\sum_{i=1}^{B}\hat{\psi}\left( u \right) =\hat{\psi}\left( u \right), \\ Var^{MC}\left( \hat{\psi}_{B}\left( u \right) \right) &= \frac{1}{B^2} \sum_{i=1}^{B}Var^{MC}\left( \mathbf{1}\left\{ R^{\ast (i)}\leq u\right\} \right) \\ &= \frac{1}{B^2}\sum_{i=1}^{B}P^{\ast}\left( R^{\ast (i) }\leq u \right) \left[ 1-P^{\ast}\left( R^{\ast (i)}\leq u \right) \right] = \\ &= \frac{1}{B^2}\sum_{i=1}^{B}\hat{\psi}\left( u \right) \left( 1-\hat{\psi} \left( u \right) \right) =\frac{1}{B}\hat{\psi}\left( u \right) \left( 1-\hat{ \psi}\left( u \right) \right) \leq \frac{1}{4B} \end{aligned}\]
Así, el error de la aproximación de Monte Carlo al bootstrap exacto (raíz cuadrada de la varianza del Monte Carlo), puede acotarse por \(\frac{1}{2\sqrt{B}}\) (para más detalles sobre la convergencia de una aproximación Monte Carlo ver p.e. el Capítulo 4 de Fernández-Casal y Cao, 2020).