5.3 Contrastes de permutaciones

Supongamos que a partir de una muestra $\left\{ \left( \mathbf{X}_i, Y_i\right): i=1,\ldots, n \right\}$ estamos interesados en contrastar la hipótesis nula de independencia entre $\mathbf{X}$ e $Y$: \[H_0: F_{Y \mid \mathbf{X}} = F_Y\] o equivalentemente que $\mathbf{X}$ no influye en la distribución de $Y$.

En este caso los valores de la respuesta serían intercambiables bajo la hipótesis nula, por lo que podríamos obtener las remuestras manteniendo fijos los valores⁶ $\mathbf{X}_i$ y permutando los $Y_i$. Es decir:

Generar $Y^{\ast}_i$, con $i=1,\ldots, n$, mediante muestreo sin reemplazamiento de $\left\{ Y_i: i=1,\ldots, n \right\}$.
Considerar la remuestra bootstrap $\left\{ \left( \mathbf{X}_i, Y^{\ast}_i\right): i=1,\ldots, n \right\}$.

Se pueden realizar contrastes de este tipo con el paquete boot estableciendo el parámetro sim = "permutation" al llamar a la función boot() (el argumento i de la función statistic contendrá permutaciones del vector de índices). Puede ser también de interés el paquete coin, que implementa muchos contrastes de este tipo.

5.3.1 Ejemplo: Inferencia sobre el coeficiente de correlación lineal

En esta sección consideraremos como ejemplo el conjunto de datos dogs del paquete boot, que contiene observaciones sobre el consumo de oxígeno cardíaco (mvo) y la presión ventricular izquierda (lvp) de 7 perros domésticos.

library(boot)
data('dogs', package = "boot")
# plot(dogs)

Supongamos que estamos interesados en estudiar la correlación lineal entre las variables mvo ($X$) y lvp ($Y$). Para ello podemos considerar el coeficiente de correlación lineal de Pearson: \[\rho =\frac{ Cov \left( X, Y \right) } { \sigma \left( X \right) \sigma \left( Y \right) }\] Su estimador es el coeficiente de correlación muestral: \[r=\frac{\sum_{i=1}^{n}(x_i-\overline{x})(y_i-\overline{y})} {\sqrt{ \sum_{i=1}^{n}(x_i-\overline{x})^{2}} \sqrt{\sum_{i=1}^{n}(y_i-\overline{y})^{2}}},\] que podemos calcular en R empleando la función cor():

cor(dogs$mvo, dogs$lvp)

## [1] 0.8536946

# with(dogs, cor(mvo, lvp))

Para realizar inferencias sobre $\rho$ podemos emplear la función cor.test():

cor.test(dogs$mvo, dogs$lvp)

## 
##  Pearson's product-moment correlation
## 
## data:  dogs$mvo and dogs$lvp
## t = 3.6655, df = 5, p-value = 0.01451
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.2818014 0.9780088
## sample estimates:
##       cor 
## 0.8536946

# with(dogs, cor.test(mvo, lvp))

Esta función realiza el contraste $H_0: \rho = 0$ empleando el estadístico: \[\frac{r\sqrt{n - 2}}{\sqrt{1 - r^2}} \underset{aprox}{\sim } t_{n-2},\] bajo la hipótesis nula de que la verdadera correlación es cero. Alternativemente se pueden realizar contrastes unilaterales estableciendo el parámetro alternative igual a "less" o "greater". Por ejemplo, para contrastar $H_0: \rho \leq 0$ podríamos emplear:

cor.test(dogs$mvo, dogs$lvp, alternative = "greater")

## 
##  Pearson's product-moment correlation
## 
## data:  dogs$mvo and dogs$lvp
## t = 3.6655, df = 5, p-value = 0.007255
## alternative hypothesis: true correlation is greater than 0
## 95 percent confidence interval:
##  0.4195889 1.0000000
## sample estimates:
##       cor 
## 0.8536946

Para realizar el contraste con la función boot podríamos emplear el siguiente código:

library(boot)

statistic <- function(data, i) cor(data$mvo, data$lvp[i])

set.seed(1)
res.boot <- boot(dogs, statistic, R = 1000, sim = "permutation")
# res.boot

Posteriormente emplearíamos las réplicas (almacenadas en res.boot$t) y el valor observado del estadístico del contraste (almacenado en res.boot$t0) para aproximar el $p$-valor:

hist(res.boot$t, freq = FALSE)
abline(v = res.boot$t0, lty = 2)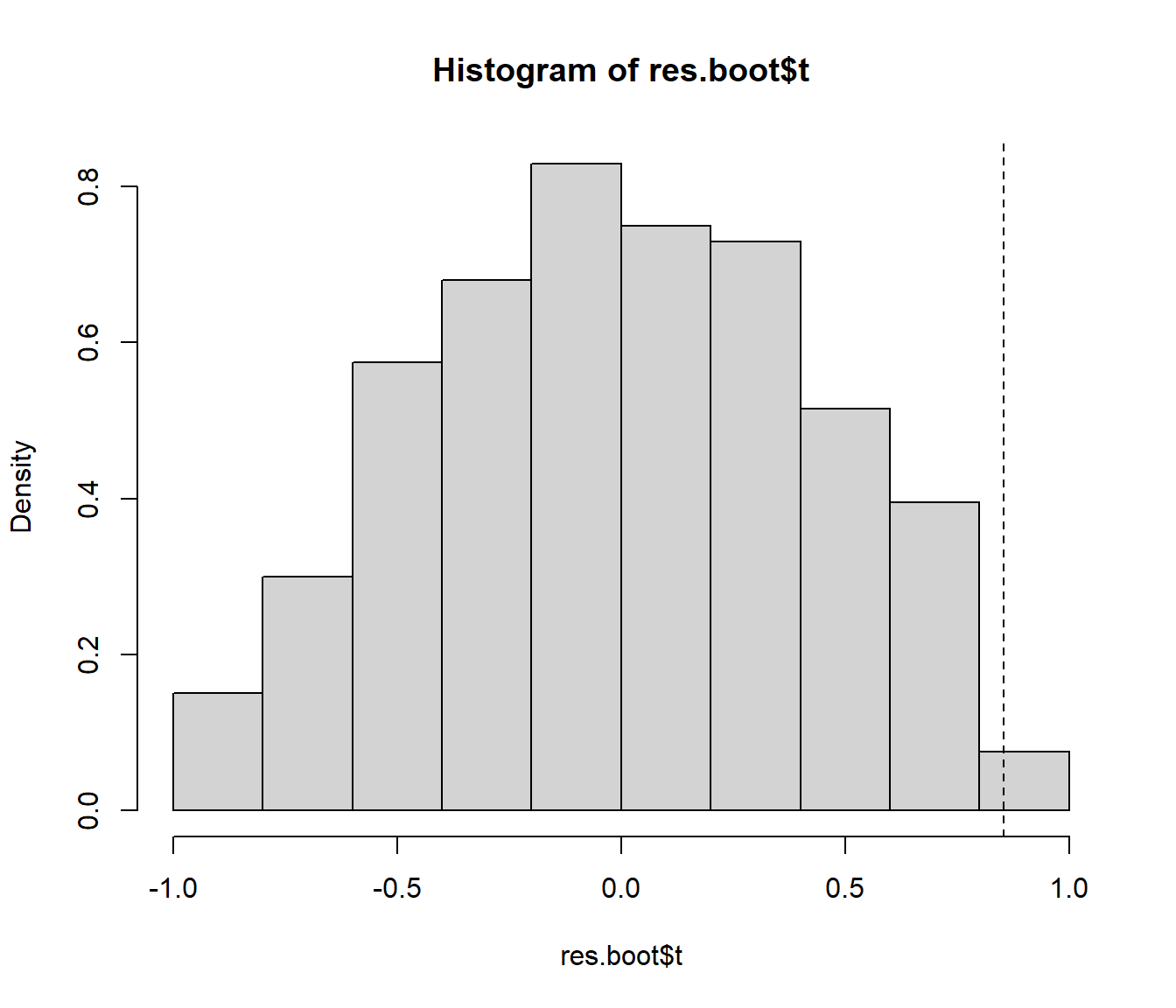

Por ejemplo, para el contraste unilateral $H_0: \rho \leq 0$ (alternative = "greater"), obtendríamos:

pval.greater <- mean(res.boot$t >= res.boot$t0)
pval.greater

## [1] 0.009

Mientras que para realizar el contraste bilateral $H_0: \rho = 0$ (alternative = "two.sided"), sin asumir que la distribución del estadístico de contraste es simétrica:

pval.less <- mean(res.boot$t <= res.boot$t0)
pval <- 2*min(pval.less, pval.greater)
pval

## [1] 0.018

Nótese que no se hace ninguna suposición sobre el tipo de covariables, podrían ser categóricas, numéricas o una combinación de ambas.↩︎