1.1 Introducción

El bootstrap es un procedimiento estadístico que sirve para aproximar la distribución en el muestreo (normalmente) de un estadístico. Para ello procede mediante remuestreo, es decir, obteniendo muestras mediante algún procedimiento aleatorio que utilice la muestra original.

Su ventaja principal es que no requiere hipótesis sobre el mecanismo generador de los datos. Sí las requiere, aunque suelen ser más relajadas, para obtener propiedades asintóticas del mismo. Por otra parte, su implementación en ordenador suele ser sencilla, en comparación con otros métodos. Su principal inconveniente es la necesidad de computación intensiva, debido a la fuerza bruta del método de Monte Carlo. Con la capacidad computacional actual, esta mayor carga computacional del bootstrap no suele ser un problema hoy en día. En raras ocasiones el bootstrap no necesita del uso de técnicas de Monte Carlo.

1.1.1 Breve nota histórica

Precursores teóricos remotos:

  • Laplace (1810). Teoría límite de primer orden.

  • Chebychev (final siglo XIX). Teoría límite de segundo orden.

Primeras contribuciones:

  • Hubback (1878-1968). Esquemas de muestreo espacial para ensayos agrícolas.

  • Mahalanobis (años 1930 y segunda guerra mundial). Precursor del bootstrap por bloques.

Otras contribuciones:

  • Gurney, McCarthy, Hartigan (años 1960, 1970). Métodos de half-sampling para estimación de varianzas (U.S. Bureau of the Census).

  • Maritz, Jarret, Simon (años 1970, 1980). Métodos de permutaciones relacionados con el bootstrap.

En la actualidad:

  • Bradley Efron (Stanford University, 1979). Creador oficial del método. Acuñó su nombre. Fusionó la potencia de Monte Carlo con la resolución de problemas planteados de forma muy general.

  • Peter Hall (1951-2016). Fue uno de los estadísticos contemporáneos más prolíficos. Dedicó al bootstrap gran parte de su producción a partir de los años 1980.

1.1.2 Paradigma inferencial y análogo bootstrap

Paradigma inferencial

Suponemos que \(\mathbf{X}=\left( X_1,\ldots ,X_n \right)\) es una m.a.s. de una población con distribución \(F\) y que estamos interesados en hacer inferencia sobre \(\theta =\theta \left(F \right)\). Para ello nos gustaría conocer la distribución en el muestreo de \(R\left( \mathbf{X},F \right)\), cierto estadístico función de la muestra y de la distribución poblacional. Por ejemplo: \[R=R\left( \mathbf{X},F \right) =\theta \left( F_n \right) -\theta \left( F \right) = \hat \theta - \theta,\] siendo \(F_n\) la función de distribución empírica.

A veces podemos calcular directamente la distribución de \(R\left( \mathbf{X},F \right)\), aunque suele depender de cantidades poblacionales, no conocidas en la práctica. Por ejemplo, bajo normalidad \(X_i \overset{i.i.d.}{\sim} \mathcal{N}\left( \mu ,\sigma^2 \right)\), si estamos interesados en \[\theta \left( F \right) =\mu =\int x~dF\left( x \right) =\int xf\left( x \right) ~dx\] como \(\theta \left( F_n \right) = \int x~dF_n\left( x \right) = \sum \frac{1}{n}X_i = \bar{X}\), podríamos considerar el estadístico: \[R=R\left( \mathbf{X},F \right) = \bar{X} - \mu \sim \mathcal{N}\left( 0 ,\frac{\sigma^2}{n} \right).\] Aunque en la práctica la varianza no es normalmente conocida y habría que aproximarla (sería preferible considerar como estadístico la media estudentizada).

Otras veces sólo podemos llegar a aproximar la distribución de \(R\left( \mathbf{X},F \right)\) cuando \(n \rightarrow \infty\). Por ejemplo, cuando estamos interesados en la media pero desconocemos la distribución de los datos.

Análogo bootstrap

El primer paso es reemplazar la distribución poblacional (desconocida) \(F\) por una estimación, \(\hat{F}\), de la misma. Por ejemplo, podríamos considerar la distribución empírica \(\hat{F}=F_n\) (bootstrap uniforme; Sección 1.2), o una aproximación paramétrica \(\hat{F}=F_{\hat \theta}\) (bootstrap paramétrico; Sección 3.1).

Como ejemplo ilustrativo consideramos los datos simulados :

set.seed(1)
muestra <- rnorm(100)
hist(muestra, freq = FALSE, xlim = c(-3, 3),
     main = '', xlab = 'x', ylab = 'densidad')
curve(dnorm, lty = 2, add = TRUE)
Distribución de la muestra simulada.

Figura 1.1: Distribución de la muestra simulada.

Como aproximación de la distribución poblacional, desconocida en la práctica, siempre podemos considerar la distribución empírica (o una versión suavizada: bootstrap suavizado; Sección 3.3). Alternativamente podríamos asumir un modelo paramétrico y estimar los parámetros a partir de la muestra .

# Distribución bootstrap uniforme
curve(ecdf(muestra)(x), xlim = c(-3, 3), ylab = "F(x)", type = "s")
# Distribución bootstrap paramétrico (asumiendo normalidad)
curve(pnorm(x, mean(muestra), sd(muestra)), lty = 2, add = TRUE)
# Distribución teórica
curve(pnorm, lty = 3, add = TRUE)
legend("bottomright", legend = c("Empírica", "Aprox. paramétrica", "Teórica"), lty = 1:3)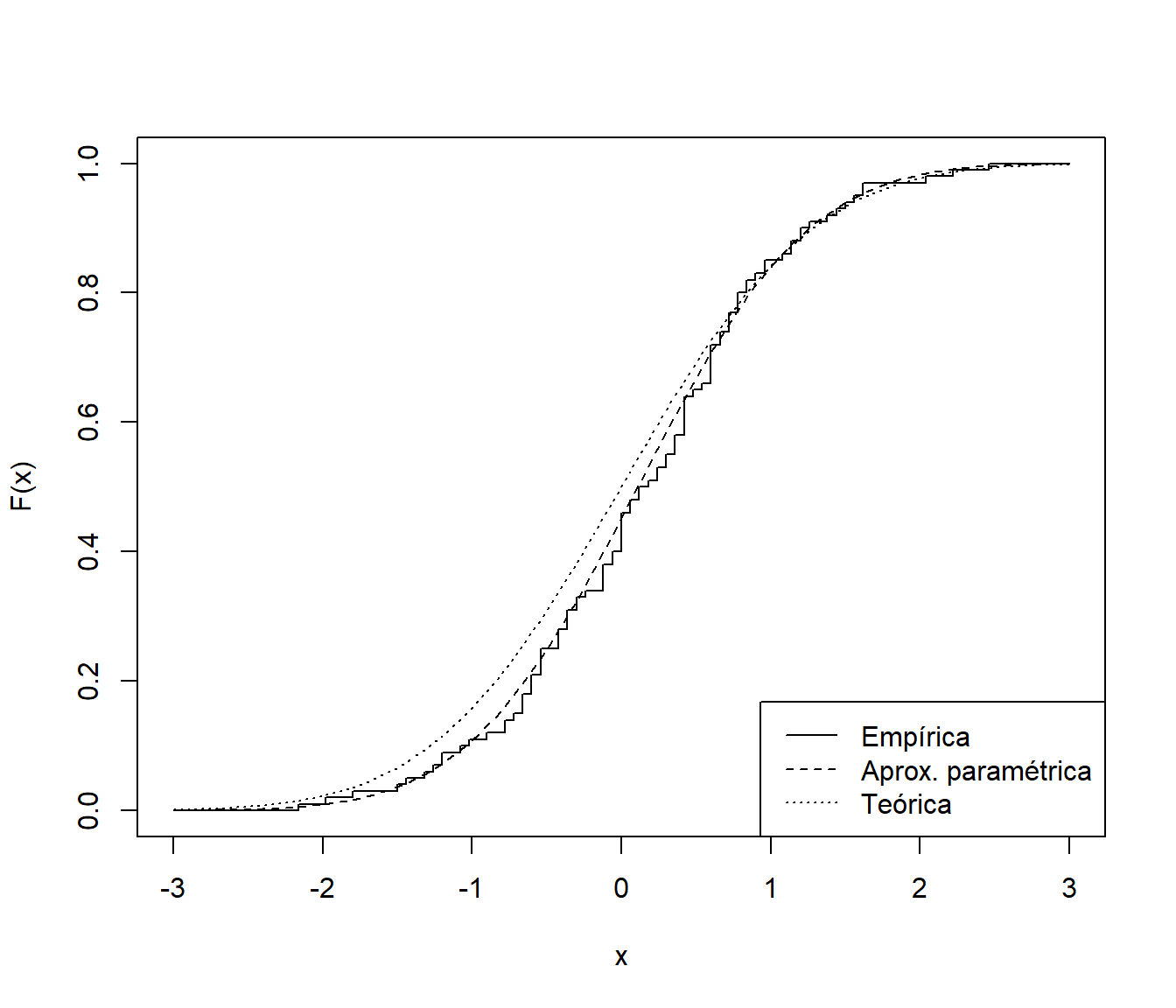
Distribución teórica de la muestra simulada y distintas aproximaciones.

Figura 1.2: Distribución teórica de la muestra simulada y distintas aproximaciones.

A partir de la aproximación \(\hat{F}\) podríamos generar, condicionalmente a la muestra observada, remuestras \[\mathbf{X}^{\ast}=\left( X_1^{\ast},\ldots ,X_n^{\ast} \right)\] con distribución \(X_i^{\ast} \sim \hat{F}\), que demoninaremos remuestras bootstrap. Por lo que podemos hablar de la distribución en el remuestreo de \[R^{\ast}=R\left( \mathbf{X}^{\ast},\hat{F} \right),\] llamada distribución bootstrap.

La idea original (Efron, 1979) es que la distribución de \(\hat{\theta}_{b}^{\ast }\) en torno a \(\hat{\theta}\) aproxima la distribución de \(\hat{\theta}\) en torno a \(\theta\). Por tanto se pretende aproximar la distribución en el muestreo de \(R\) por la distribución bootstrap de \(R^{\ast}\).

En raras ocasiones la distribución bootstrap de \(R^{\ast}\) es calculable directamente, pero siempre suele poder aproximarse por Monte Carlo.

1.1.3 Implementación en la práctica

En el caso i.i.d., si empleamos como aproximación la distribución empírica \(\hat{F}=F_n\), la generación de las muestras bootstrap puede hacerse mediante remuestreo (manteniendo el tamaño muestral). Habría que simular una muestra de tamaño \(n\) de una variable aleatoria discreta que toma los valores \(X_1,\ldots ,X_n\) todos ellos con probabilidad \(\frac{1}{n}\):

  • Para cada \(i=1,\ldots, n\), \(P^{\ast}\left( X_i^{\ast}=X_j \right) = \frac{1}{n}\), \(j=1,\ldots ,n\).

Existen multitud de algoritmos para simular variables discretas, pero en este caso de equiprobabilidad hay un procedimiento muy eficiente (método de la transformación cuantil con búsqueda directa) que se reduce a simular un número aleatorio \(U\), con distribución \(\mathcal{U}\left( 0,1 \right)\), y hacer \(X^{\ast}=X_{\left\lfloor nU\right\rfloor +1}\), donde \(\left\lfloor x\right\rfloor\) representa la parte entera de \(x\), es decir, el mayor número entero que sea menor o igual que \(x\). Empleando ese método, el procedimiento para generar la muestra bootstrap sería:

  • Para cada \(i=1,\ldots ,n\) generar \(U_i\sim \mathcal{U}\left( 0,1 \right)\) y hacer \(X_i^{\ast}=X_{\left\lfloor nU_i\right\rfloor +1}\).
set.seed(1)
n <- length(muestra)
u <- runif(n)
muestra_boot <- muestra[floor(n*u) + 1]
head(muestra_boot)
## [1] -0.1557955 -0.0593134 -1.0441346 -0.5425200  0.9189774  0.2670988

En R es recomendable1 emplear la función sample para generar muestras aleatorias con reemplazamiento del conjunto de datos original:

muestra_boot <- sample(muestra, replace = TRUE)
head(muestra_boot)
## [1] -1.4707524  0.7685329  0.3876716 -0.6887557  0.9189774  1.3586796

En el caso multidimensional, cuando trabajamos con un conjunto de datos con múltiples variables, podríamos emplear un procedimiento análogo, a partir de remuestras del vector de índices. Por ejemplo:

data(iris)
str(iris)
## 'data.frame':    150 obs. of  5 variables:
##  $ Sepal.Length: num  5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
##  $ Sepal.Width : num  3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
##  $ Petal.Length: num  1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
##  $ Petal.Width : num  0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
##  $ Species     : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
n <- nrow(iris)
# i_boot <- floor(n*runif(n)) + 1
# i_boot <- sample.int(n, replace = TRUE)
i_boot <- sample(n, replace = TRUE)
data_boot <- iris[i_boot, ]
str(data_boot)
## 'data.frame':    150 obs. of  5 variables:
##  $ Sepal.Length: num  6.9 7.2 4.3 6.4 5.7 5.8 7.2 5.6 5.8 5.4 ...
##  $ Sepal.Width : num  3.1 3.2 3 3.2 4.4 4 3 2.9 2.7 3.9 ...
##  $ Petal.Length: num  5.4 6 1.1 5.3 1.5 1.2 5.8 3.6 5.1 1.3 ...
##  $ Petal.Width : num  2.1 1.8 0.1 2.3 0.4 0.2 1.6 1.3 1.9 0.4 ...
##  $ Species     : Factor w/ 3 levels "setosa","versicolor",..: 3 3 1 3 1 1 3 2 3 1 ...

Esta forma de proceder es la que emplea por defecto el paquete boot que describiremos más adelante (Sección 1.4.1).

Ejemplo 1.1 (Inferencia sobre la media con varianza conocida)

Hemos observado 15 tiempos de vida de microorganismos: 0.143, 0.182, 0.256, 0.260, 0.270, 0.437, 0.509, 0.611, 0.712, 1.04, 1.09, 1.15, 1.46, 1.88, 2.08. A partir de los cuales queremos obtener una estimación por intervalo de confianza de su vida media, suponiendo que la desviación típica es conocida e igual a 0.6 (en el Capítulo 4 se tratará con más detalle la construcción de intervalos de confianza). 
muestra <- c(0.143, 0.182, 0.256, 0.26, 0.27, 0.437, 0.509, 
    0.611, 0.712, 1.04, 1.09, 1.15, 1.46, 1.88, 2.08)
sigma <- 0.6
summary(muestra)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  0.1430  0.2650  0.6110  0.8053  1.1200  2.0800
sd(muestra)
## [1] 0.6237042
hist(muestra)
rug(muestra)
Distribución del tiempo de vida de microorganismos.

Figura 1.3: Distribución del tiempo de vida de microorganismos.

Contexto clásico

Suponemos que los datos \(\mathbf{X}=\left( X_1,\ldots ,X_n \right)\) son una m.a.s. de una población con distribución \(F\), con \(\mu\) desconocida y \(\sigma\) conocida, y que estamos interesados en hacer inferencia sobre: \[\theta \left( F \right) =\mu =\int x~dF\left( x \right)\] Para ello, un estadístico adecuado para este caso es: \[R=R\left( \mathbf{X},F \right) =\sqrt{n}\frac{\bar{X}-\mu }{\sigma},\] con \(\theta \left( F_n \right) =\int x~dF_n\left( x \right) = \bar{X}\).

Bajo normalidad \(\left( X\sim \mathcal{N}\left( \mu ,\sigma^2 \right) \right)\), \(R\sim N\left( 0,1 \right)\). Si \(F\) no es normal, tan sólo sabemos que, bajo ciertas condiciones, \(R\overset{d}{\rightarrow }\mathcal{N}\left( 0, 1 \right)\).

A partir de esta última aproximación, se obtiene el intervalo de confianza asintótico (de nivel \(1-\alpha\)) para la media \(\mu\): \[\hat{IC}_{1-\alpha}\left( \mu\right) = \left( \overline{X}-z_{1-\alpha/2}\dfrac{\sigma}{\sqrt{n}},\ \overline{X} + z_{1-\alpha/2}\dfrac{\sigma}{\sqrt{n}} \right).\]

alfa <- 0.05
x_barra <- mean(muestra)
z <- qnorm(1 - alfa/2)
n <- length(muestra)
ic_inf <- x_barra - z*sigma/sqrt(n)
ic_sup <- x_barra + z*sigma/sqrt(n)
IC <- c(ic_inf, ic_sup)
IC
## [1] 0.501697 1.108970

Contexto bootstrap

Consideramos la función de distribución empírica \(\hat{F}=F_n\) como aproximación de la distribución poblacional (bootstrap uniforme). Para aproximar la distribución bootstrap del estadístico por Monte Carlo, se generan \(B=1000\) muestras bootstrap \(\mathbf{X}^{\ast (b)}=\left( X_1^{\ast (b)},\ldots ,X_n^{\ast (b)} \right)\) de forma que \(P^{\ast (b)}\left( X_i^{\ast}=X_j \right) = \frac{1}{n}\), \(j=1,\ldots ,n\), para \(i=1,\ldots, n\) y \(b=1,\ldots, B\). A partir de las cuales se obtienen las \(B\) réplicas bootstrap del estadístico: \[R^{\ast (b)}=R\left( \mathbf{X}^{\ast (b)},\hat{F} \right) =\sqrt{n}\frac{ \bar{X}^{\ast (b)}-\bar{X}}{\sigma }, \ b=1,\ldots, B, \] con \(\bar{X}^{\ast (b)} = \frac{1}{n}\sum X_i^{\ast (b)}\).

set.seed(1)
B <- 1000
estadistico_boot <- numeric(B)
for (k in 1:B) {
    remuestra <- sample(muestra, n, replace = TRUE)
    x_barra_boot <- mean(remuestra)
    estadistico_boot[k] <- sqrt(n) * (x_barra_boot - x_barra)/sigma
}

Las características de interés de la distribución en el muestreo de \(R\) se aproximan por las correspondientes de la distribución bootstrap de \(R^{\ast}\). En este caso nos interesa aproximar los puntos críticos \(x_{\alpha /2}\) y \(x_{1-\alpha /2}\), tales que: \[P\left( x_{\alpha /2} < R < x_{1-\alpha /2} \right) = 1-\alpha.\] Para lo que podemos emplear los cuantiles muestrales2:

# Empleando la distribución empírica del estadístico bootstrap: 
estadistico_boot_ordenado <- sort(estadistico_boot)
indice_inf <- floor(B * alfa/2)
indice_sup <- floor(B * (1 - alfa/2))
pto_crit <- estadistico_boot_ordenado[c(indice_inf, indice_sup)]
# Empleando la función `quantile`:
# pto_crit <- quantile(estadistico_boot, c(alfa/2, 1 - alfa/2), type = 1)
pto_crit <- quantile(estadistico_boot, c(alfa/2, 1 - alfa/2))
pto_crit
##      2.5%     97.5% 
## -1.918622  2.075984

A partir de los cuales obtenemos la correspondiente estimación por IC boostrap: \[\hat{IC}^{boot}_{1-\alpha}\left( \mu\right) = \left( \overline{X}-x_{1-\alpha/2}\dfrac{\sigma}{\sqrt{n}},\ \overline{X} - x_{\alpha/2}\dfrac{\sigma}{\sqrt{n}} \right).\]

# Construcción del IC
ic_inf_boot <- x_barra - pto_crit[2] * sigma/sqrt(n)
ic_sup_boot <- x_barra - pto_crit[1] * sigma/sqrt(n)
IC_boot <- c(ic_inf_boot, ic_sup_boot)
names(IC_boot) <- paste0(100*c(alfa/2, 1-alfa/2), "%") # rev(names(IC_boot))
IC_boot
##      2.5%     97.5% 
## 0.4837233 1.1025650

Nótese que este intervalo de confianza no está centrado en la media, al contrario que el obtenido con la aproximación tradicional. Aunque en este caso no se observan grandes diferencias ya que la distribución bootstrap obtenida es muy similar a la aproximación normal (ver Figura 1.4).

hist(estadistico_boot, freq = FALSE)
lines(density(estadistico_boot))
abline(v = pto_crit)
curve(dnorm, lty = 2, add = TRUE)
abline(v = c(-z, z), lty = 2)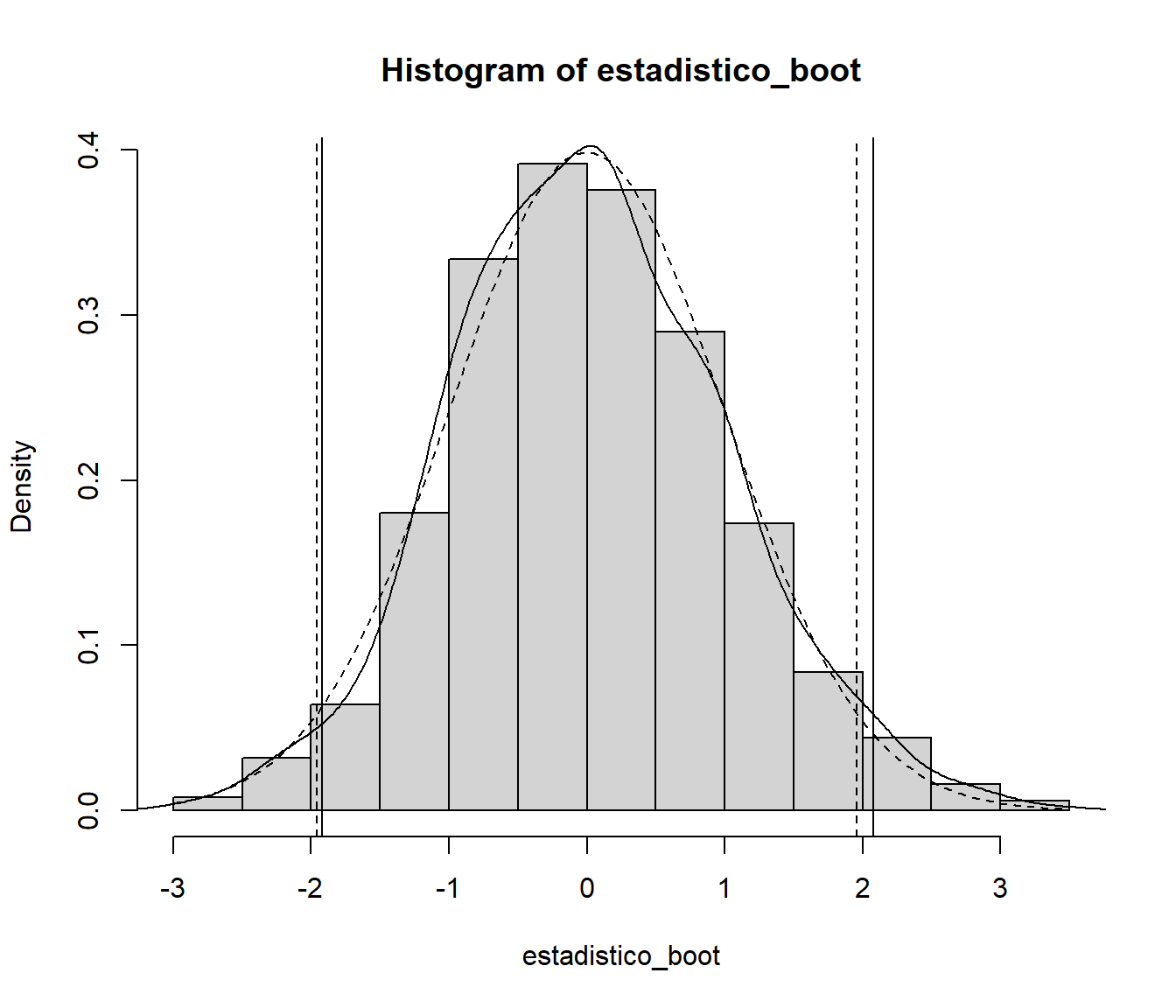
Distribución del estadístico boostrap y aproximaciones de los cuantiles. Con línea discontinua se muestra la distribución normal asintótica.

Figura 1.4: Distribución del estadístico boostrap y aproximaciones de los cuantiles. Con línea discontinua se muestra la distribución normal asintótica.

  1. De esta forma se evitan posibles problemas numéricos al emplear el método de la transformación cuantil cuando \(n\) es extremadamente grande (e.g. https://stat.ethz.ch/pipermail/r-devel/2018-September/076817.html).↩︎

  2. Se podrían considerar distintos estimadores del cuantil \(x_{\alpha}\) (ver p.e. la ayuda de la función quantile()). Si empleamos directamente la distribución empírica, el cuantil se correspondería con la observación ordenada en la posición \(B \alpha\) (se suele hacer una interpolación lineal si este valor no es entero), lo que equivale a emplear la función quantile() de R con el parámetro type = 1. Esta función considera por defecto la posición \(1 + (B - 1) \alpha\) (type = 7). En el libro de Davison y Hinkley (1997), y en el paquete boot, se emplea \((B + 1) \alpha\) (equivalente a type = 6; lo que justifica que consideren habitualmente 99, 199 ó 999 réplicas bootstrap).↩︎