7.4 Ejemplos

En esta sección nos centraremos en el bootstrap en la estimación tipo núcleo de la función de regresión, para la aproximación de la precisión y el sesgo, y también para el cálculo de intervalos de confianza y de predicción.

7.4.1 Bootstrap residual

El modelo ajustado de regresión se puede emplear para estimar la respuesta media \(m(x_0)\) cuando la variable explicativa toma un valor concreto \(x_0\). En este caso también podemos emplear el bootstrap residual (Sección 3.7.2) para realizar inferencias acerca de la media. La idea sería aproximar la distribución del error de estimación \(\hat{m}_h(x_0) - m(x_0)\) por la distribución bootstrap de \(\hat{m}^{\ast}_h(x_0) - \hat{m}_g(x_0)\).

Para reproducir adecuadamente el sesgo del estimador, la ventana \(g\) debería ser asintóticamente mayor que \(h\) (de orden \(n^{-1/5}\)). Análogamente al caso de la densidad, la recomendación sería emplear la ventana óptima para la estimación de \(m^{\prime \prime }\left( x_0 \right)\), de orden \(n^{-1/9}\) (Sección 7.2.1). Sin embargo, en la práctica es habitual emplear \(g=h\) para evitar la selección de esta ventana (lo que además facilita emplear herramientas como el paquete boot). Otra alternativa podría ser asumir que \(g \simeq n^{1/5}h/n^{1/9}\) como se hace a continuación.

n <- length(x)
g <- h * n^(4/45) # h*n^(-1/9)/n^(-1/5)
# g <- h
fitg <- locpoly(x, y, bandwidth = g) # puntos de estimación/predicción
# fitg$y <- predict(fitg, newdata = fitg$x) 
estg <- approx(fitg, xout = x)$y # puntos observaciones
# estg <- predict(fitg)
# resid2 <- y - estg # resid2 <- residuals(fitg)

# Remuestreo
set.seed(1)
B <- 2000
stat_fit_boot <- matrix(nrow = length(fit$x), ncol = B)
resid0 <- resid - mean(resid)
for (k in 1:B) {
    y_boot <- estg + sample(resid0, replace = TRUE)
    fit_boot <- locpoly(x, y_boot, bandwidth = h)$y
    stat_fit_boot[ , k] <- fit_boot - fitg$y
}

# Calculo del sesgo y error estándar 
bias <- apply(stat_fit_boot, 1, mean)
std.err <- apply(stat_fit_boot, 1, sd)

# Representar estimación y corrección de sesgo bootstrap
plot(x, y)
lines(fit, lwd = 2)
lines(fit$x, fit$y - bias)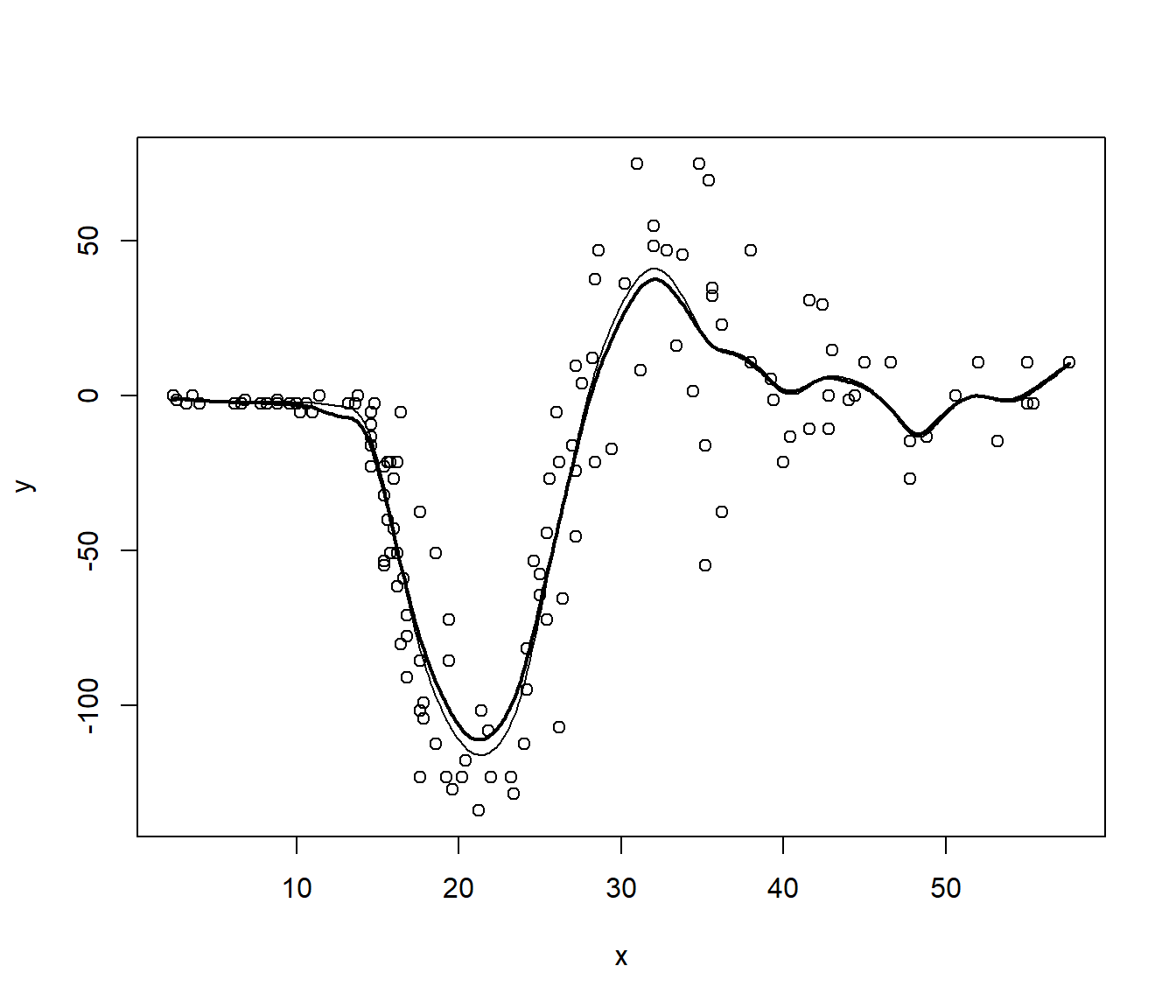

NOTA: De forma análoga al caso lineal (Sección 3.7.2), se podrían reescalar los residuos a partir de la matriz de suavizado (empleando los paquetes sm o npsp).

7.4.2 Intervalos de confianza y predicción

De forma análoga al caso de la estimación de la densidad mostrado en la Sección 6.6.2, podemos calcular estimaciones por intervalo de confianza (puntuales) por el método percentil (básico):

alfa <- 0.05
pto_crit <- apply(stat_fit_boot, 1, quantile, probs = c(alfa/2, 1 - alfa/2))
ic_inf_boot <- fit$y - pto_crit[2, ]
ic_sup_boot <- fit$y - pto_crit[1, ]

plot(x, y)
lines(fit, lwd = 2)
lines(fit$x, fit$y - bias)
lines(fit$x, ic_inf_boot, lty = 2)
lines(fit$x, ic_sup_boot, lty = 2)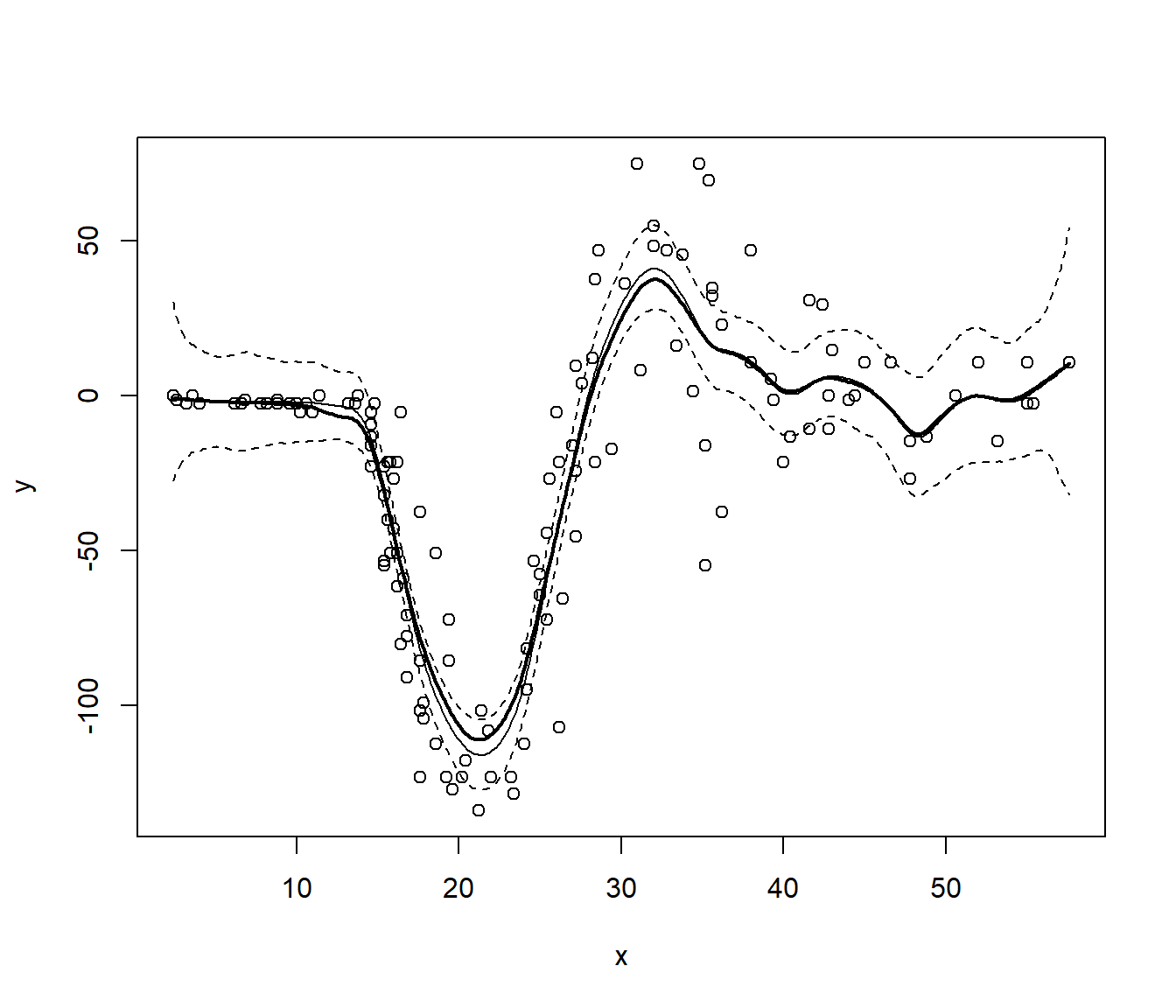

El modelo ajustado también es empleado para predecir una nueva respuesta individual \(Y(x_0)\) para un valor concreto \(x_0\) de la variable explicativa.
En el caso de errores independientes \(\hat{Y}(x_0) = \hat{m}_h(x_0)\), pero si estamos interesados en realizar inferencias sobre el error de predicción \(r(x_0) = Y(x_0) - \hat{Y}(x_0)\), a la variabilidad de \(\hat{m}_h(x_0)\) debida a la muestra, se añade la variabilidad del error \(\varepsilon(x_0)\).

La idea sería aproximar la distribución del error de predicción: \[r(x_0) = Y(x_0) - \hat{Y}(x_0) = m(x_0) + \varepsilon(x_0) - \hat{m}_h(x_0)\] por la distribución bootstrap de: \[r^{\ast}(x_0) = Y^{\ast}(x_0) - \hat{Y}^{\ast}(x_0) = \hat{m}_g(x_0) + \varepsilon^{\ast}(x_0) - \hat{m}^{\ast}_h(x_0)\]

# Remuestreo
set.seed(1)
n_pre <- length(fit$x)
stat_pred_boot <- matrix(nrow = n_pre, ncol = B)
for (k in 1:B) {
    y_boot <- estg + sample(resid0, replace = TRUE)
    fit_boot <- locpoly(x, y_boot, bandwidth = h)$y
    pred_boot <- fitg$y + sample(resid0, n_pre, replace = TRUE)
    stat_pred_boot[ , k] <- pred_boot - fit_boot
}

# Cálculo de intervalos de predicción
# por el método percentil (básico)
alfa <- 0.05
pto_crit_pred <- apply(stat_pred_boot, 1, quantile, probs = c(alfa/2, 1 - alfa/2))
ip_inf_boot <- fit$y + pto_crit_pred[1, ]
ip_sup_boot <- fit$y + pto_crit_pred[2, ]

plot(x, y, ylim = c(-150, 75))
lines(fit, lwd = 2)
lines(fit$x, fit$y - bias)
lines(fit$x, ic_inf_boot, lty = 2)
lines(fit$x, ic_sup_boot, lty = 2)
lines(fit$x, ip_inf_boot, lty = 3)
lines(fit$x, ip_sup_boot, lty = 3)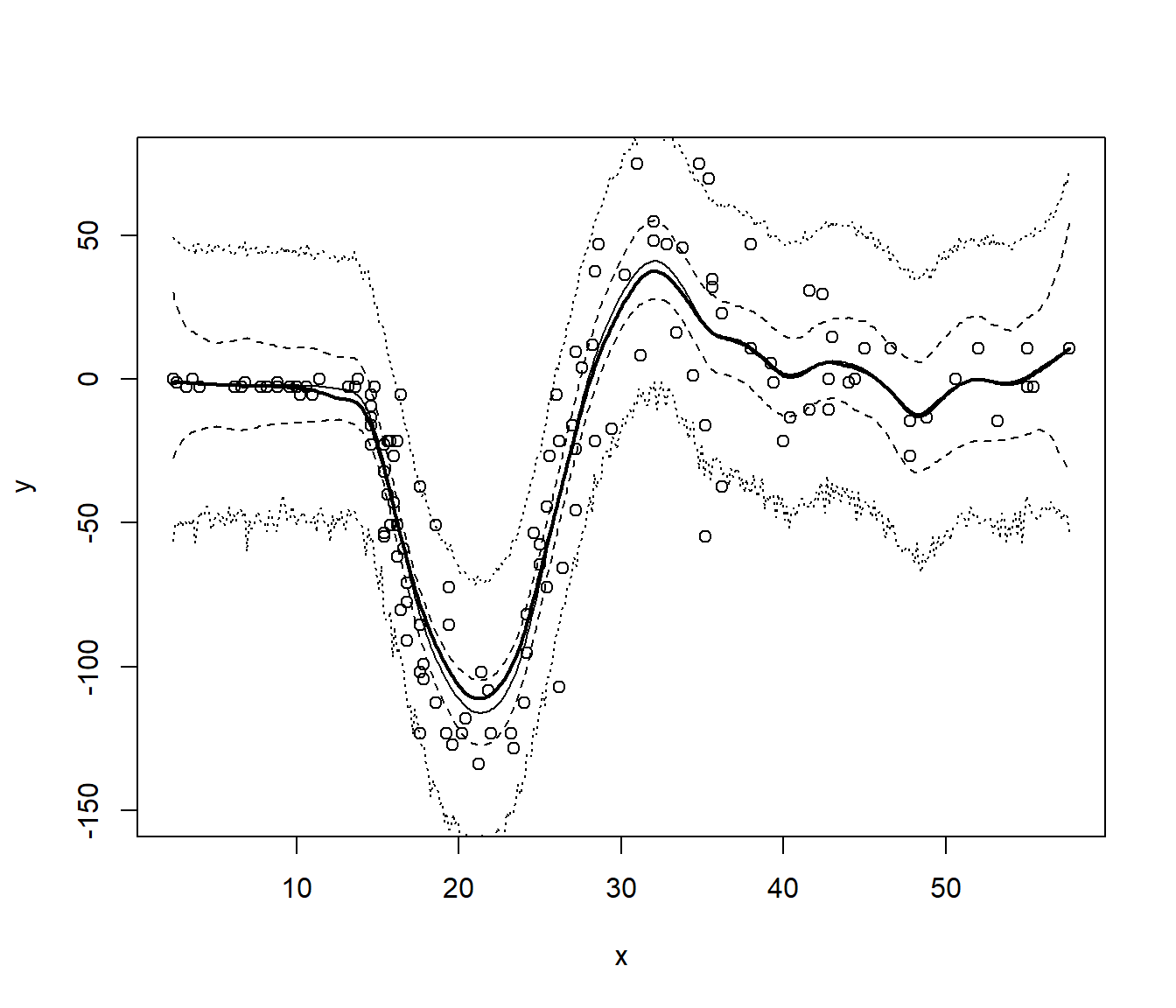

En este caso puede no ser recomendable considerar errores i.i.d., sería de esperar heterocedásticidad (e incluso dependencia temporal). El bootstrap residual se puede extender al caso heterocedástico y/o dependencia (e.g. Castillo-Páez et al., 2019, 2020).

7.4.3 Wild bootstrap

Como se describe en la Sección 7.2.1 en el caso heterocedástico se puede emplear wild bootstrap.

# Remuestreo
set.seed(1)
B <- 1000
fit_boot <- matrix(nrow = n_pre, ncol = B)
for (k in 1:B) {
        rwild <- sample(c((1 - sqrt(5))/2, (1 + sqrt(5))/2), n, replace = TRUE, 
                        prob = c((5 + sqrt(5))/10, 1 - (5 + sqrt(5))/10))
    y_boot <- estg + resid*rwild
    fit_boot[ , k] <- locpoly(x, y_boot, bandwidth = h)$y
    # OJO: bootstrap percetil directo
}
        

# Calculo del sesgo y error estándar
bias <- apply(fit_boot, 1, mean, na.rm = TRUE) - fitg$y
std.err <- apply(fit_boot, 1, sd, na.rm = TRUE)

# Representar estimación y corrección de sesgo bootstrap
plot(x, y)
lines(fit, lwd = 2)
lines(fit$x, fit$y - bias)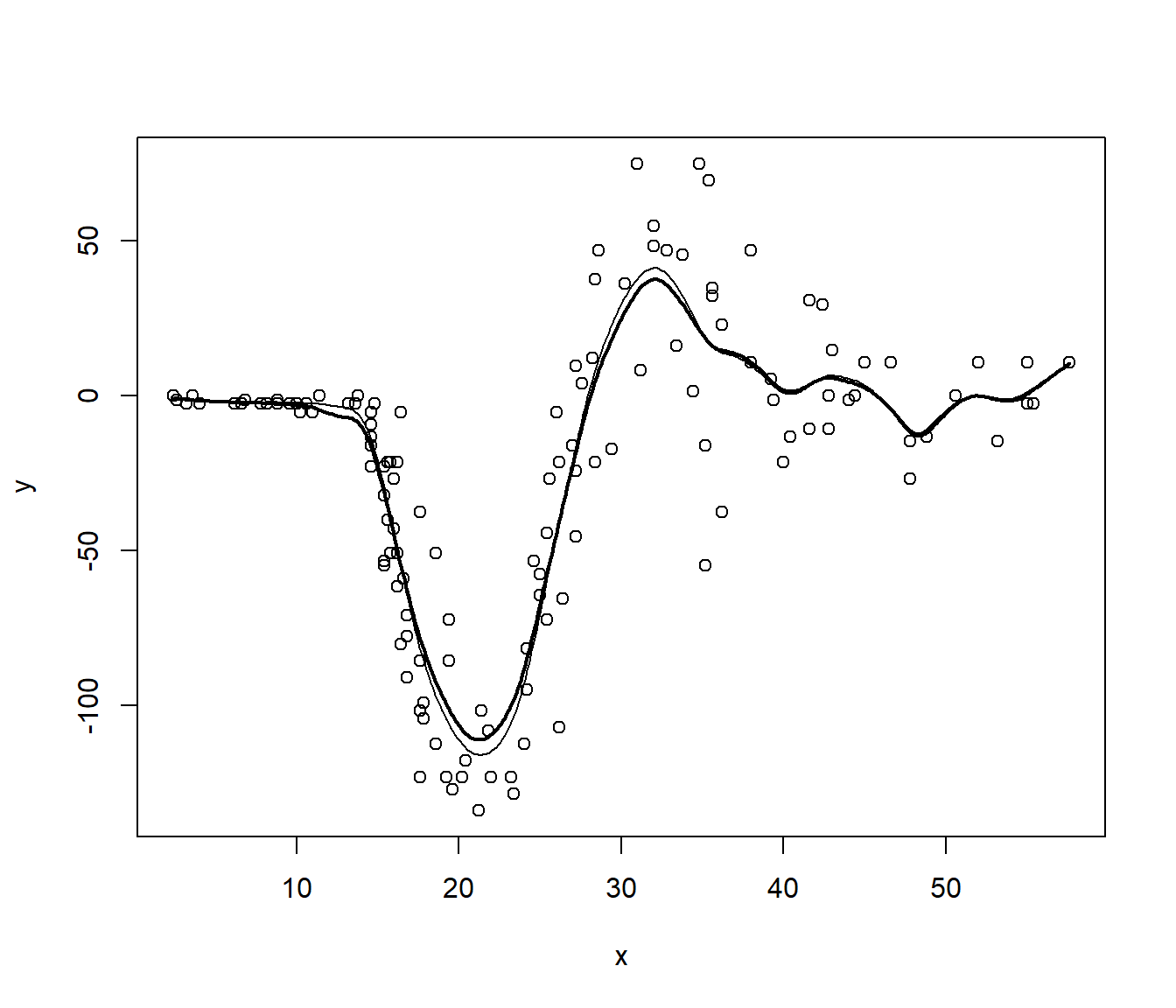

7.4.4 Ejercicio

Siguiendo con el conjunto de datos MASS::mcycle, emplear wild bootstrap para obtener estimaciones por intervalo de confianza de la función de regresión de accel a partir de times mediante bootstrap percentil básico. Comparar los resultados con los obtenidos mediante bootstrap residual (comentar las diferencias y cuál de las aproximaciones sería más adecuada para este caso).