3.3 Bootstrap suavizado

Cuando la distribución poblacional, \(F\), es continua es lógico incorporar dicha información al bootstrap. Eso significa que la función de distribución tiene una función de densidad asociada, relacionadas mediante la expresión: \(f\left( x \right) =F^{\prime}\left( x \right)\). Para ello, debemos utilizar un método bootstrap que remuestree de un universo bootstrap continuo. En otras palabras debemos utilizar un estimador de la función de densidad y remuestrear de él.

Pasamos a considerar brevemente el problema de estimar, no paramétricamente, la función de densidad, \(f\), de una población, a partir de una muestra, \(\left( X_1,X_2,\ldots ,X_n \right)\), procedente de la misma. En ese contexto es bien conocido el método histograma (basado en el cual sería posible idear un método bootstrap) aunque es más recomendable utilizar el estimador tipo núcleo propuesto por Parzen (1962) y Rosenblatt (1956), que viene dado por

\[\hat{f}_{h}\left( x \right) =\frac{1}{nh}\sum_{i=1}^{n}K\left( \frac{x-X_i}{ h} \right) =\frac{1}{n}\sum_{i=1}^{n}K_{h}\left( x-X_i \right),\]

donde \[K_{h}\left( u \right) =\frac{1}{h}K\left( \frac{u}{h} \right),\] \(K\) es una función núcleo (normalmente una densidad simétrica en torno al cero) y \(h>0\) es una parámetro de suavizado, llamado ventana, que regula el tamaño del entorno que se usa para llevar a cabo la estimación. Este estimador generaliza el bien conocido histograma y, más concretamente, su versión histograma móvil. Así, eligiendo como función \(K\) la densidad de una \(\mathcal{U}\left( -1,1 \right)\), el estimador de Parzen-Rosenblatt resulta: \[\begin{aligned} \frac{1}{nh}\sum_{i=1}^{n}\frac{1}{2}\mathbf{1}\left\{ \frac{x-X_i}{h}\in \left( -1,1 \right) \right\} &= \frac{1}{2nh}\sum_{i=1}^{n}\mathbf{1}\left\{ X_i\in \left( x-h,x+h \right) \right\} \\ &= \frac{\#\left\{ X_i\in \left( x-h,x+h \right) \right\} }{2nh}, \end{aligned}\] que no es más que la frecuencia relativa de datos \(X_i\) en el intervalo \(\left( x-h,x+h \right)\) dividida entre la longitud del intervalo en cuestión (\(2h\)).

Es habitual exigir que la función núcleo \(K\) sea no negativa y su integral sea uno: \[K\left( u \right) \geq 0,~\forall u,~\int_{-\infty }^{\infty }K\left(u \right) du=1.\] Además también es frecuente exigir que \(K\) sea una función simétrica (\(K\left( -u \right) =K\left( u \right)\)).

Aunque la elección de la función \(K\) no tiene gran impacto en las propiedades del estimador (salvo sus condiciones de regularidad: continuidad, diferenciabilidad, etc.) la elección del parámetro de suavizado sí es muy importante para una correcta estimación. En otras palabras, el tamaño del entorno usado para la estimación no paramétrica debe ser adecuado (ni demasiado grande ni demasiado pequeño).

En R podemos emplear la función density() del paquete base para obtener una estimación tipo núcleo de la densidad (con la ventana determinada por el parámetro bw), aunque podríamos emplear implementaciones de otros paquetes (en la Sección 6.5 se incluyen más detalles). Por ejemplo, considerando el conjunto de datos precip (que contiene el promedio de precipitación, en pulgadas de lluvia, de 70 ciudades de Estados Unidos), podríamos utilizar el siguiente código :

x <- precip
npden <- density(x)
# npden <- density(x, bw = "SJ")

# plot(npden)
bandwidth <- npden$bw
hist(x, freq = FALSE, main = "Kernel density estimation", 
     xlab = paste("Bandwidth =", formatC(bandwidth)), lty = 2, 
     border = "darkgray", xlim = c(0, 80), ylim = c(0, 0.08))
lines(npden, lwd = 2)
rug(x, col = "darkgray")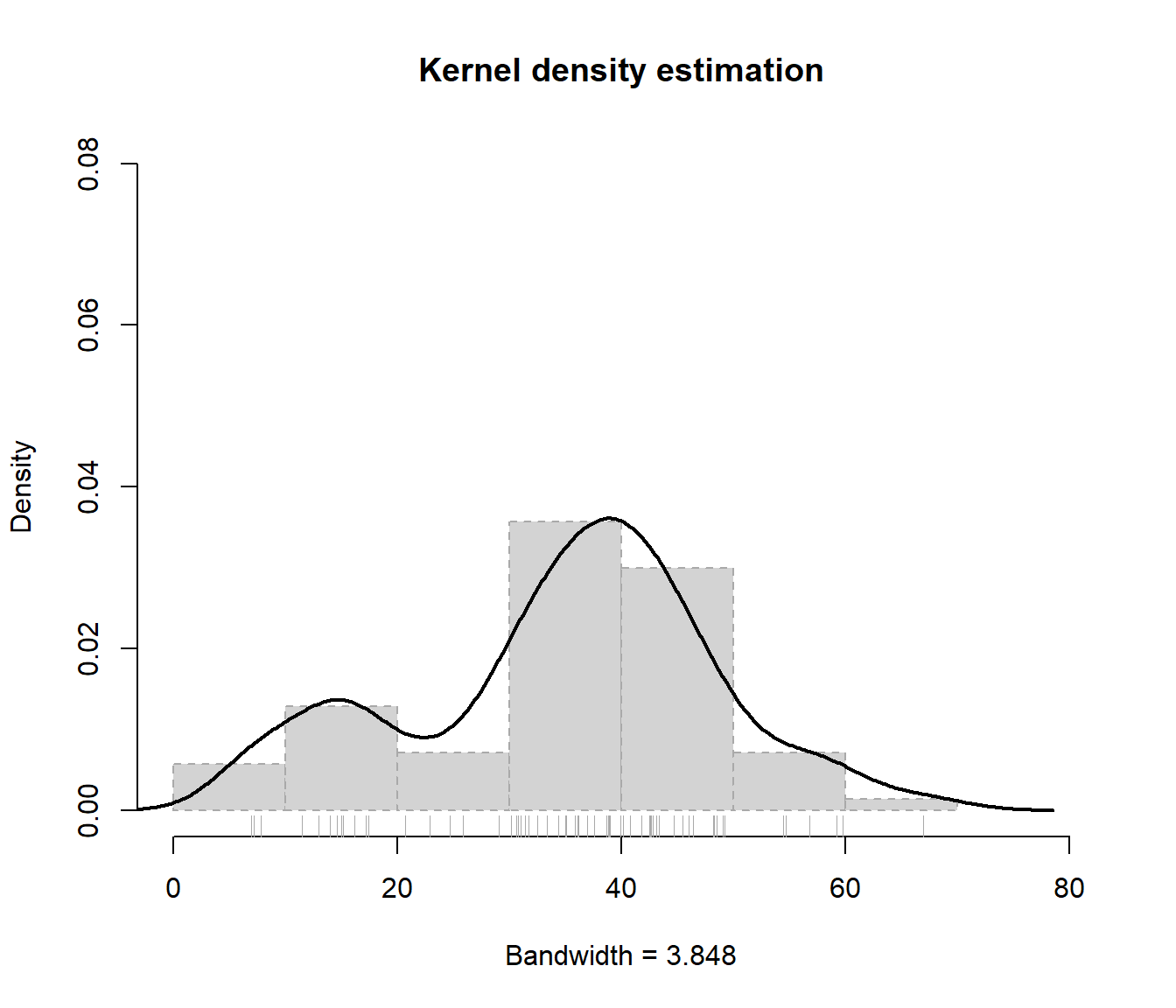
Estimación tipo núcleo de la densidad de `precip`.

Figura 3.2: Estimación tipo núcleo de la densidad de precip.

La sensibilidad del estimador tipo núcleo al parámetro de suavizado puede observarse ejecutando el siguiente código (ver Figura 3.3, bandwidth-movie.gif):

bws <- 2^seq(log2(bandwidth * 0.01), log2(bandwidth * 20), len = 50)
bws <- c(bws, rev(bws))
for (bw in bws)
  plot(density(x, bw = bw) , main = "Kernel density estimation", 
         xlab = paste("Bandwidth =", formatC(bw)), 
         xlim = c(0, 80), ylim = c(0, 0.08))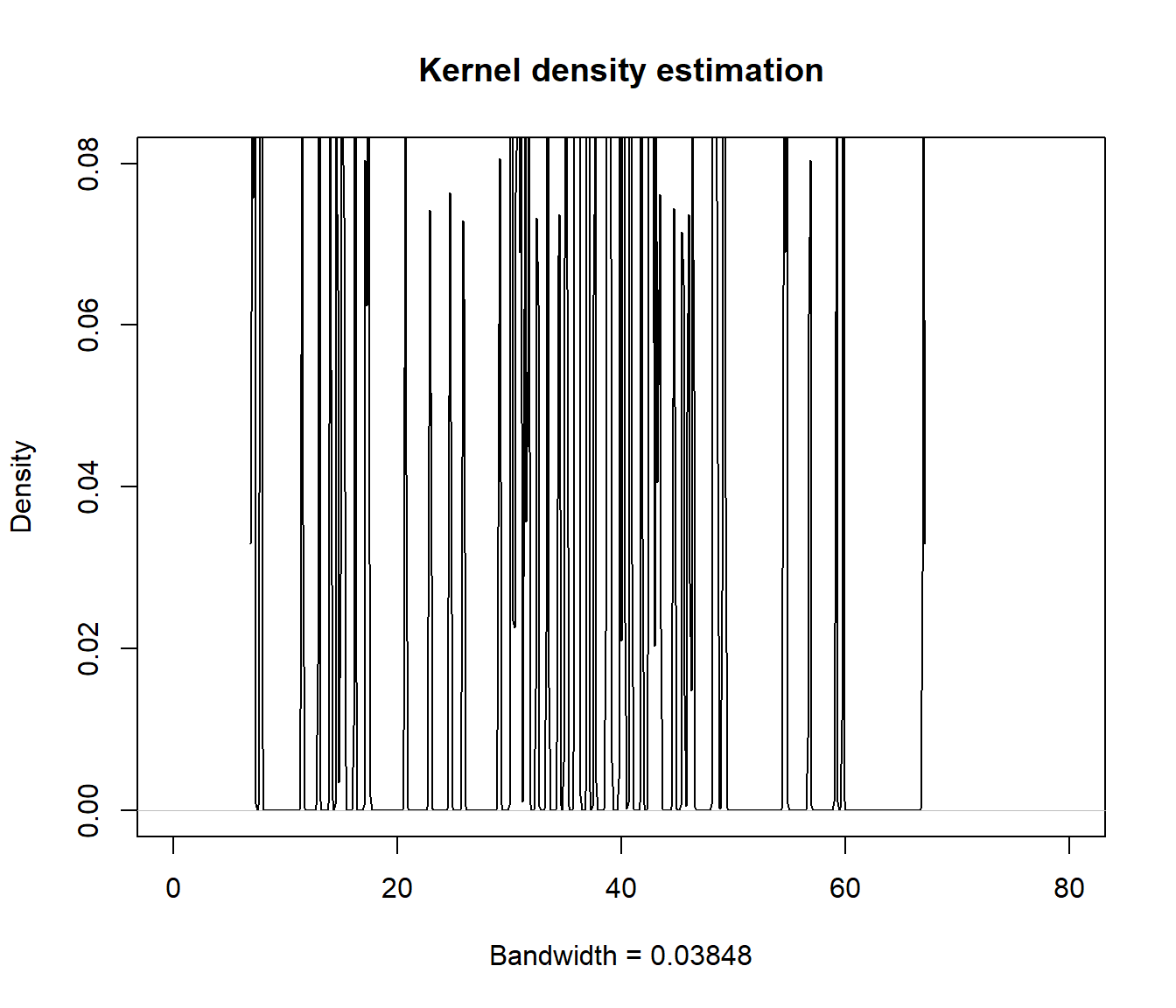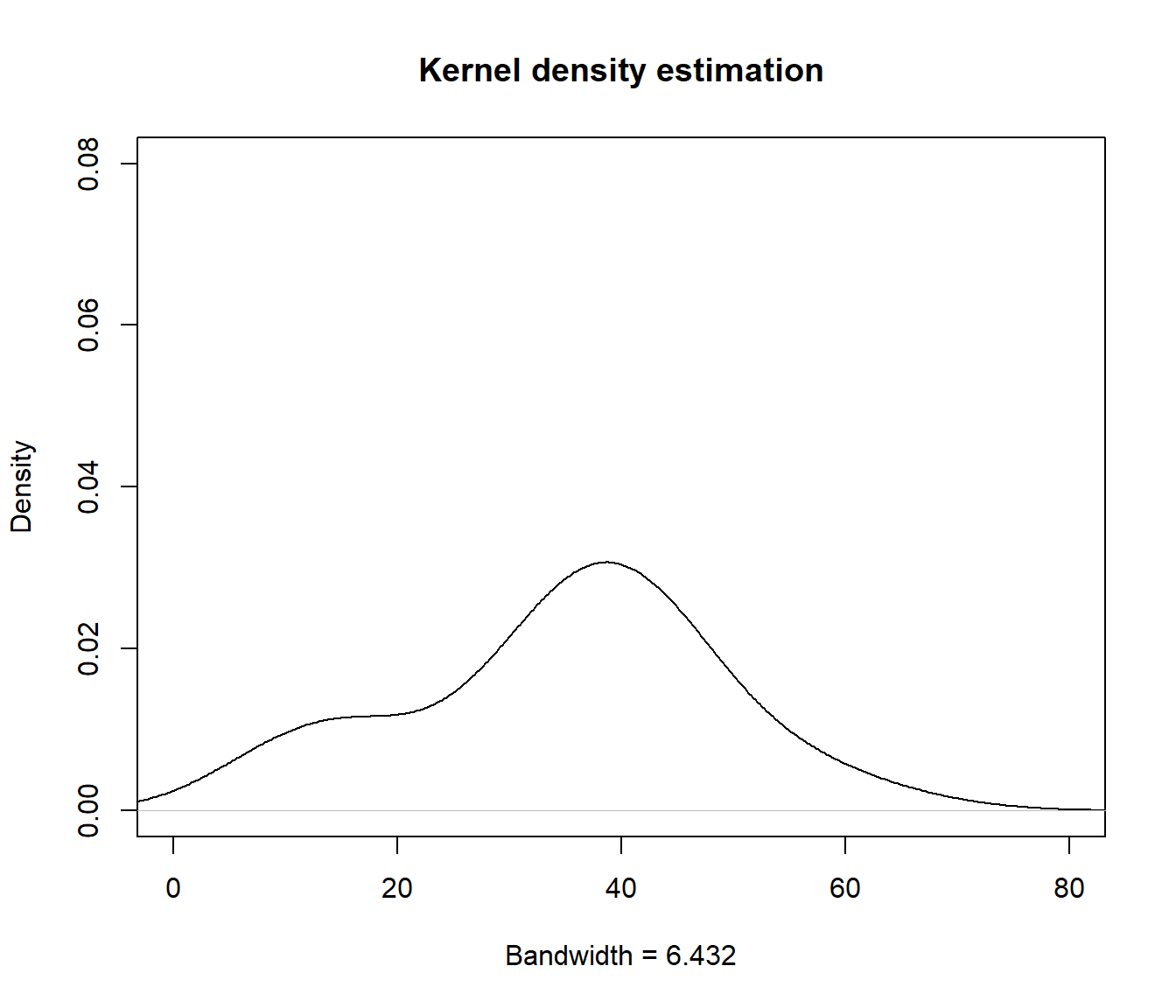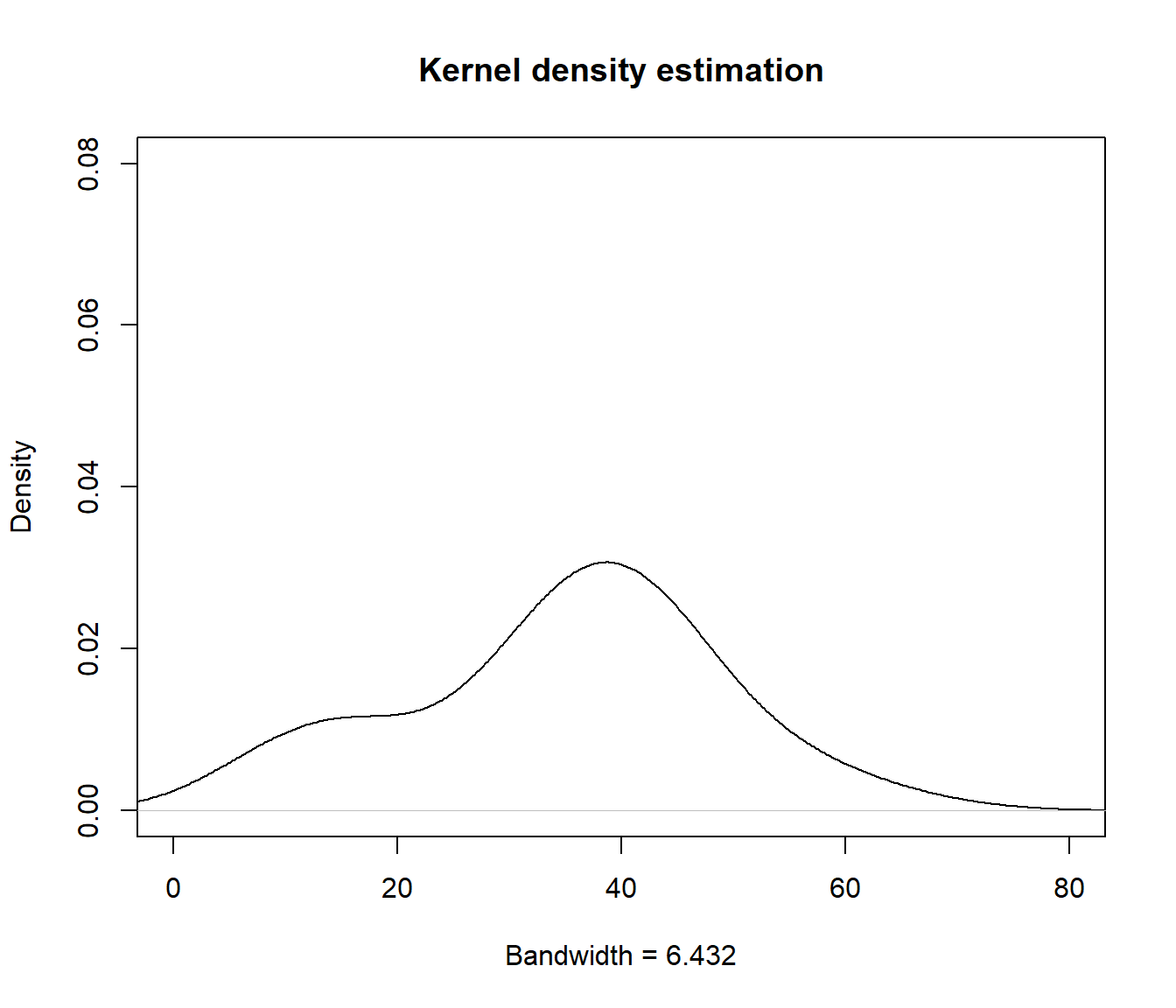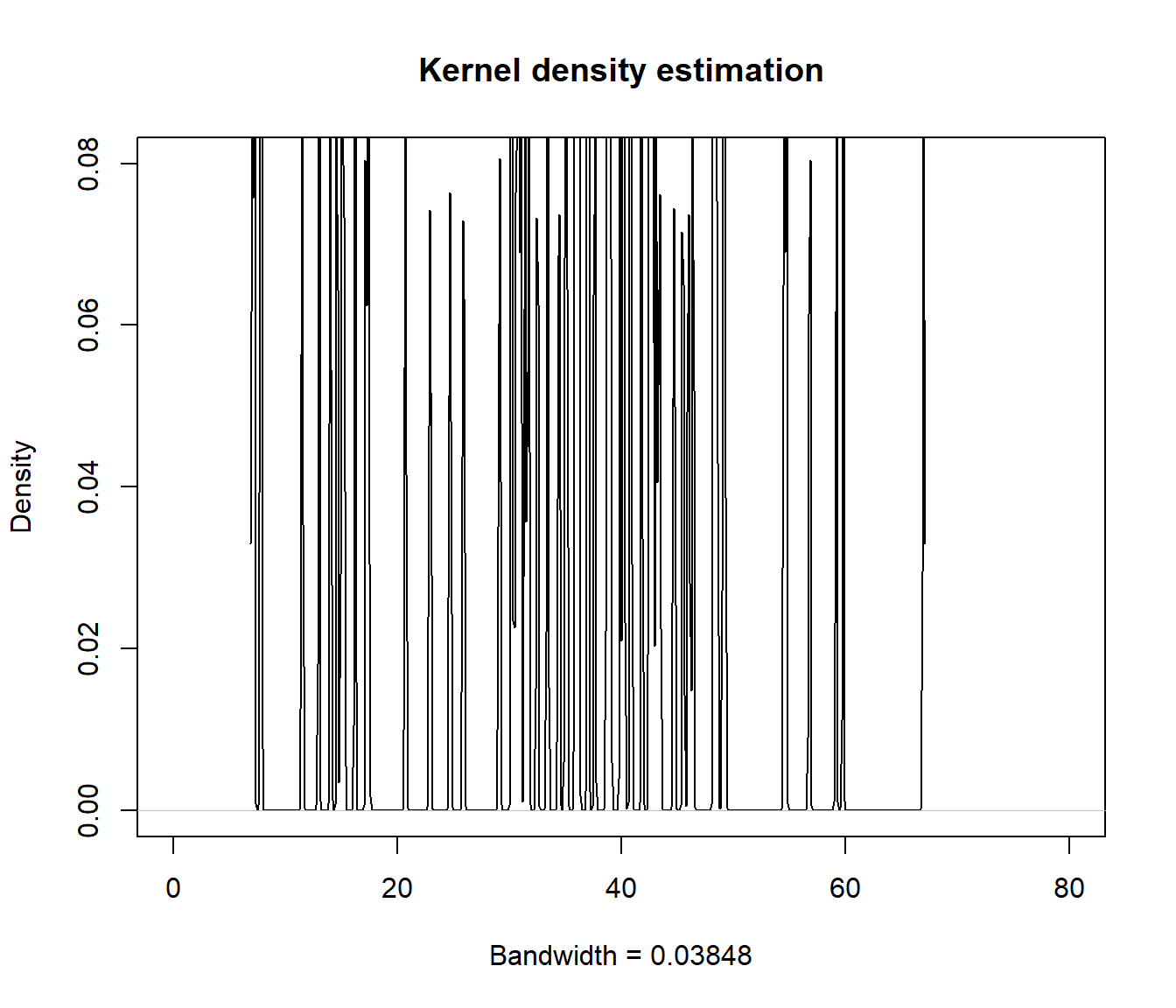
Efecto de cambio en la ventana en la estimación tipo núcleo de la densidad.

Figura 3.3: Efecto de cambio en la ventana en la estimación tipo núcleo de la densidad.

La función de distribución asociada al estimador tipo núcleo de la función de densidad viene dada por \[\begin{aligned} \hat{F}_{h}\left( x \right) &= \int_{-\infty }^{x}\hat{f}_{h}\left( y \right) dy =\int_{-\infty }^{x}\frac{1}{n}\sum_{i=1}^{n}\frac{1}{h} K\left( \frac{y-X_i}{h} \right) dy \\ &= \frac{1}{nh}\sum_{i=1}^{n}\int_{-\infty }^{x} K\left( \frac{y-X_i}{h} \right) dy \\ &= \frac{1}{n}\sum_{i=1}^{n}\int_{-\infty }^{\frac{x-X_i}{h}}K\left( u \right) du =\frac{1}{n}\sum_{i=1}^{n}\mathbb{K}\left( \frac{x-X_i}{h} \right) \end{aligned}\] donde \(\mathbb{K}\) es la función de distribución asociada al núcleo \(K\), es decir \[\mathbb{K}\left( t \right) =\int_{-\infty }^{t}K\left( u \right) du.\]

Por ejemplo, en el caso de del conjunto de datos de precipitaciones, el siguiente código compara la estimación tipo núcleo de la distribución con la empírica :

Fn <- ecdf(precip)
curve(Fn, xlim = c(0, 75), ylab = "F(x)", type = "s")
Fnp <- function(x) sapply(x, function(y) mean(pnorm(y, precip, bandwidth)))
curve(Fnp, lty = 2, add = TRUE) 
legend("bottomright", legend = c("Empírica", "Tipo núcleo"), lty = 1:2)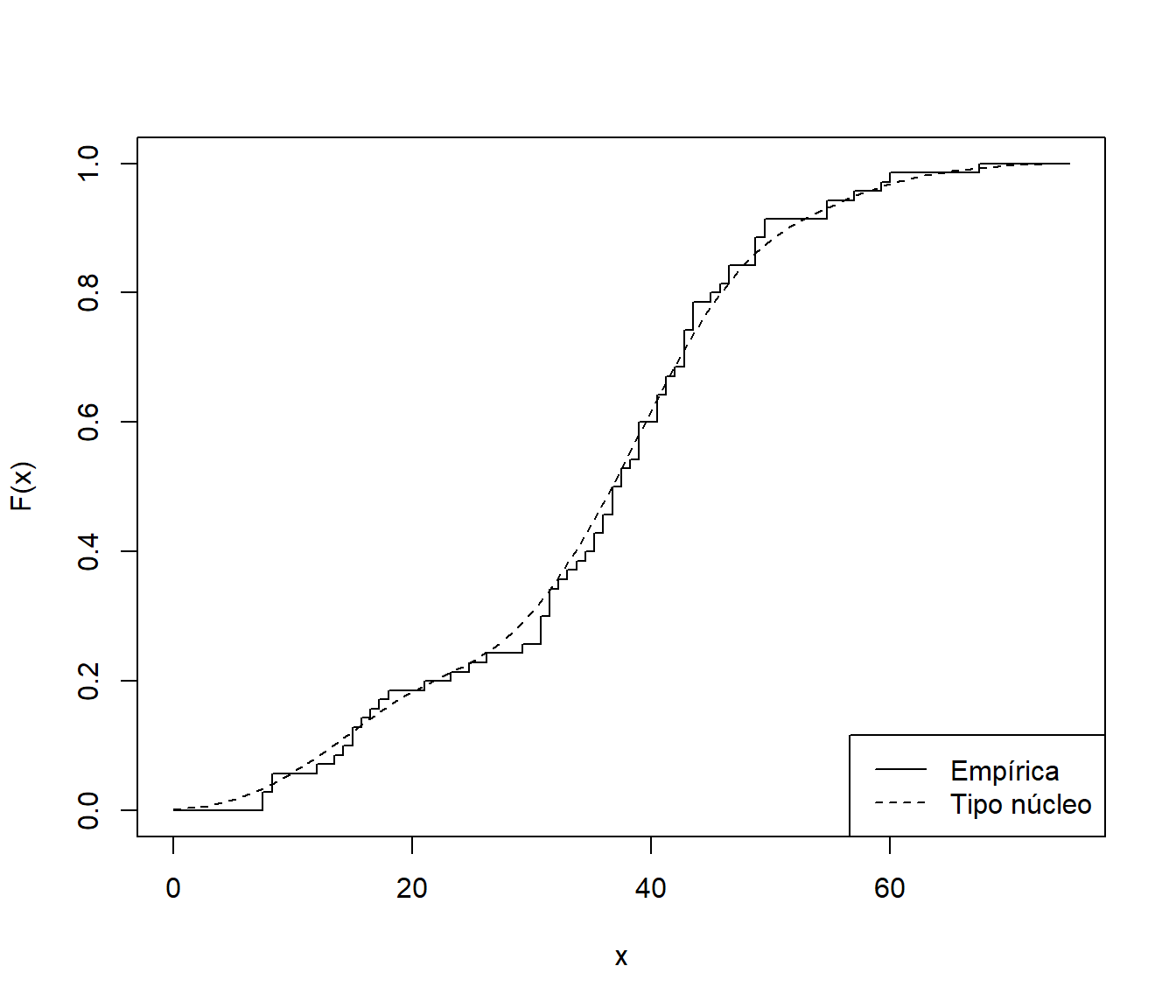
Estimación empírica y tipo núcleo de la función de distribución de `precip`.

Figura 3.4: Estimación empírica y tipo núcleo de la función de distribución de precip.

El método bootstrap suavizado procede de la siguiente forma:

  1. A partir de la muestra \(\left( X_1,X_2,\ldots ,X_n \right)\) y utilizando un valor \(h>0\) como parámetro de suavizado, se calcula el estimador de Parzen-Rosenblatt \(\hat{f}_{h}\)

  2. Se arrojan remuestras bootstrap \(\mathbf{X}^{\ast}=\left( X_1^{\ast},X_2^{\ast},\ldots ,X_n^{\ast} \right)\) a partir de la densidad \(\hat{f}_{h}\)

  3. Calcular \(R^{\ast}=R\left( \mathbf{X}^{\ast},\hat{F}_{h} \right)\)

  4. Repetir \(B\) veces los pasos 2-3 para obtener las réplicas bootstrap \(R^{\ast (1)}\), \(\ldots\), \(R^{\ast (B)}\)

Para llevar a cabo un bootstrap que remuestree a partir del estimador \(\hat{f}_{h}\left( x \right)\) es útil pensar en dicho estimador como una combinación lineal convexa de funciones de densidad, \(K_{h}\left( x-X_i \right)\), cada una con coeficiente \(\frac{1}{n}\) en dicha combinación lineal. Gracias a esa representación podemos simular valores, \(X^{\ast}\), procedentes de \(\hat{f}_{h}\left( x \right)\) en dos pasos (empleando el denominado método de composición; ver p.e. Fernández-Casal y Cao, 2020, Sección 5.4).

En un primer paso elegiremos (aleatoriamente y con equiprobabilidad) cuál de los índices \(i\in \left\{ 1,\ldots ,n\right\}\) vamos a considerar y en un segundo paso simularemos \(X^{\ast}\) a partir de la densidad \(K_{h}\left( \cdot -X_i \right)\). Esta última fase puede relacionarse fácilmente con la simulación de un valor, \(V\), con densidad \(K\), sin más que hacer \(X_i+hV\). Así, el paso 2 del algoritmo previo puede llevarse a cabo mediante el siguiente procedimiento:

  1. Para cada \(i=1,\ldots ,n\) arrojar \(U_i\sim \mathcal{U}\left( 0,1 \right)\) y \(V_i\) con densidad \(K\) y hacer \(X_i^{\ast}=X_{\left\lfloor nU_i\right\rfloor +1}+hV_i\)

La equivalencia de ambas presentaciones del paso 2 viene dada por el siguiente razonamiento. Denotando \(U\sim \mathcal{U}\left( 0,1 \right)\), \(I=\left\lfloor nU\right\rfloor +1\) y \(V\sim K\), independiente de \(U\), se tiene:

\[\begin{aligned} P^{\ast}\left( X^{\ast}\leq x \right) &= \sum_{i=1}^{n}P^{\ast}\left( \left. X^{\ast}\leq x\right\vert _{I=i} \right) P^{\ast}\left( I=i \right) \\ &= \sum_{i=1}^{n}P^{\ast}\left( \left. X_i+hV\leq x\right\vert _{I=i} \right) P^{\ast}\left( I=i \right) \\ &= \sum_{i=1}^{n}P^{\ast}\left( \left. V\leq \frac{x-X_i}{h} \right\vert _{X_i} \right) \frac{1}{n}=\frac{1}{n}\sum_{i=1}^{n}\mathbb{K} \left( \frac{x-X_i}{h} \right), \end{aligned}\]

cuya función de densidad es, como ya sabemos, \(\hat{f}_{h}\left( x \right)\). Esto justifica la presentación alternativa del paso 2, de forma que el bootstrap suavizado puede pensarse, a partir del bootstrap uniforme (\(X_i^{\ast}=X_{\left\lfloor nU_i\right\rfloor +1}\)) añadiendo al mismo una perturbación (\(hV_i\)) cuya magnitud viene dada por el parámetro de suavizado (\(h\)) y cuya forma imita a la de una variable aleatoria (\(V_i\)) con densidad \(K\).

Por ejemplo, la función density() emplea por defecto un núcleo gaussiano, y como se muestra en la ayuda de esta función, podemos emplear un código como el siguiente para obtener nsim simulaciones (ver Figura 3.5):

## simulation from a density() fit:
# a kernel density fit is an equally-weighted mixture.
nsim <- 1e6
set.seed(1)
# x_boot <- sample(x, nsim, replace = TRUE)
# x_boot <- x_boot + bandwidth * rnorm(nsim)
x_boot <- rnorm(nsim, sample(x, nsim, replace = TRUE), bandwidth)

plot(npden, main = "")
lines(density(x_boot), col = "blue", lwd = 2, lty = 2)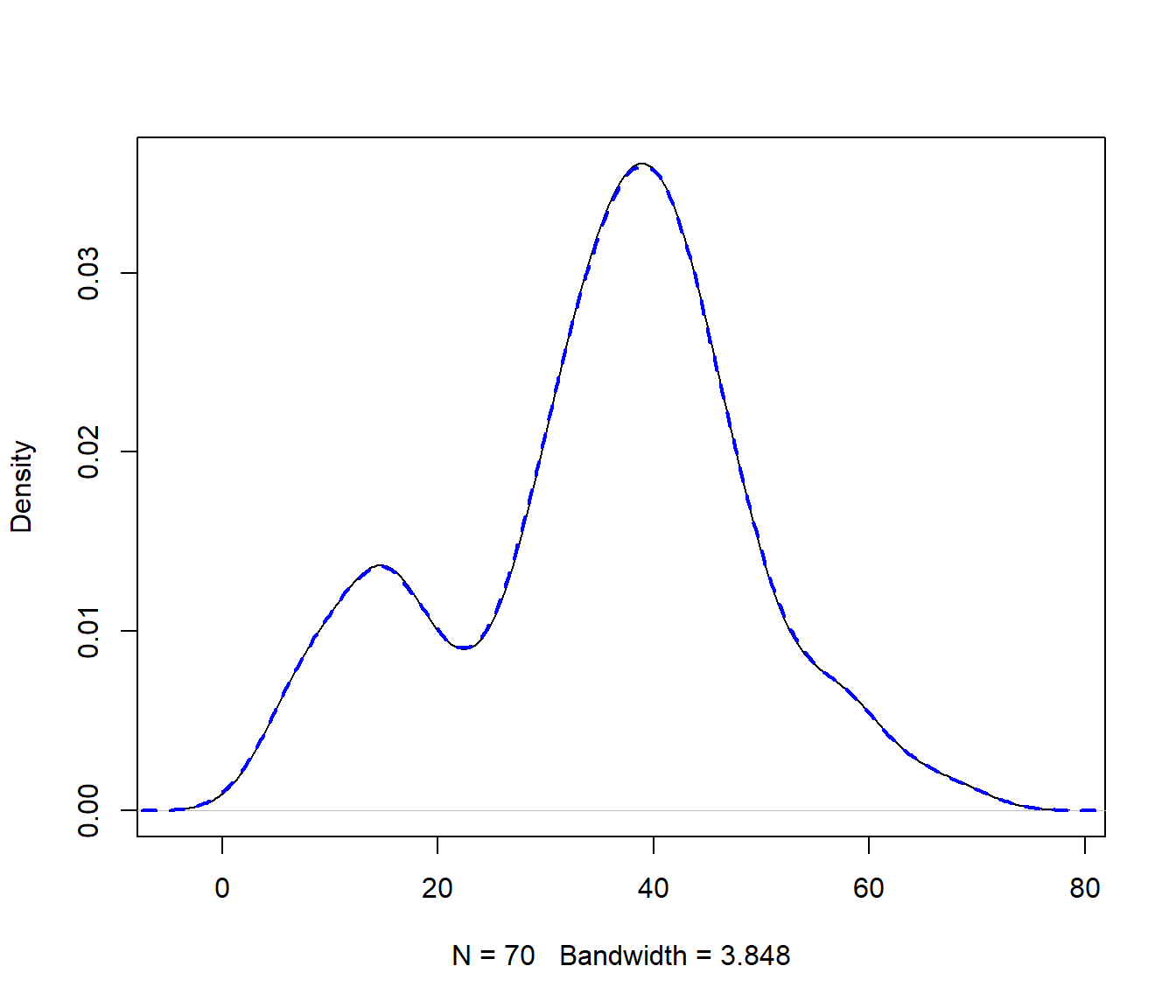
Estimaciónes tipo núcleo de las densidades de `precip` y de una simulación.

Figura 3.5: Estimaciónes tipo núcleo de las densidades de precip y de una simulación.

Es fácil percatarse de que los posibles valores que puede tomar una observación \(X_i^{\ast}\) de cada remuestra bootstrap son infinitos, pues la variable \(V\) puede tomar infinitos posibles valores, según la densidad de probabilidad \(K\). Esto significa que la distribución en el remuestreo de la remuestra bootstrap, \(\mathbf{X}^{\ast}\), es mucho más complicada que para el bootstrap uniforme. En particular no es discreta y por tanto no puede caracterizarse a partir de vectores de remuestreo sobre la muestra original. Un problema importante es la elección del parámetro de suavizado, \(h\), en este procedimiento de remuestreo. En la práctica es razonable elegir \(h\) como un valor bastante pequeño, en relación con la desviación típica de la muestra. Es fácil observar que en el caso extremo \(h=0\) este método de remuestreo se reduce al bootstrap uniforme.

Ejemplo 3.2 (Inferencia sobre la media con varianza conocida, continuación) Continuando con el ejemplo de tiempo de vida de microorganismos, podemos modificar fácilmente el código mostrado en el Ejemplo 1.1, para implementar bootstrap suavizado con función núcleo gaussiana, para calcular un intervalo de confianza para la media poblacional con desviación típica conocida:

muestra <- c(0.143, 0.182, 0.256, 0.26, 0.27, 0.437, 0.509, 
             0.611, 0.712, 1.04, 1.09, 1.15, 1.46, 1.88, 2.08)
n <- length(muestra)
sigma <- 0.6

alfa <- 0.05
x_barra <- mean(muestra)

# Remuestreo
set.seed(1)
B <- 1000
# h <- 1e-08
h <- bw.SJ(muestra)/2
estadistico_boot <- numeric(B)
for (k in 1:B) {
    # remuestra <- sample(muestra, n, replace = TRUE)
    # remuestrasu <- remuestra + h * rnorm(n, 0, 1)
    remuestrasu <- rnorm(n, sample(muestra, n, replace = TRUE), h)
    x_barra_boot <- mean(remuestrasu)
    estadistico_boot[k] <- sqrt(n) * (x_barra_boot - x_barra)/sigma
}

# Aproximación bootstrap de los ptos críticos
pto_crit <- quantile(estadistico_boot, c(alfa/2, 1 - alfa/2))

# Construcción del IC
ic_inf_boot <- x_barra - pto_crit[2] * sigma/sqrt(n)
ic_sup_boot <- x_barra - pto_crit[1] * sigma/sqrt(n)
IC_boot <- c(ic_inf_boot, ic_sup_boot)
names(IC_boot) <- paste0(100*c(alfa/2, 1-alfa/2), "%")
IC_boot
##      2.5%     97.5% 
## 0.4668897 1.0798549

Con el paquete boot, la recomendación es implementarlo como un bootstrap paramétrico:

library(boot)
ran.gen.smooth <- function(data, mle) {
    # Función para generar muestras aleatorias mediante 
    # bootstrap suavizado con función núcleo gaussiana,
    # mle contendrá la ventana.
    n <- length(data)
    h <- mle
    out <- rnorm(n, sample(data, n, replace = TRUE), h)
    out
}

statistic <- function(data){
    c(mean(data), sigma^2/length(data))
}

set.seed(1)
res.boot <- boot(muestra, statistic, R = B, sim = "parametric",
                 ran.gen = ran.gen.smooth, mle = h)

boot.ci(res.boot, type = "stud")
## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = res.boot, type = "stud")
## 
## Intervals : 
## Level    Studentized     
## 95%   ( 0.4664,  1.0830 )  
## Calculations and Intervals on Original Scale