8.1 Introducción a los datos censurados
Considérese una variable de interés, \(X\), no negativa que no siempre es posible observar (por ejemplo un tiempo de vida) pues, en ocasiones, ocurre otro fenómeno previo, cuyo tiempo hasta su ocurrencia, \(C\), puede ser anterior a la variable de interés (es decir, \(C<X\)). Cuando \(X\) es un tiempo de vida ante una enfermedad mortal, la variable \(C\) suele representar el tiempo hasta el fin del estudio, el tiempo hasta que el individuo fallezca por otra causa o el tiempo hasta que se produce una pérdida de seguimiento. Es habitual definir el indicador de no censura \(\delta =\mathbf{1}_{\left\{ X\leq C\right\} }\). Si \(C<X\) diremos que la observación es censurada y sólo seremos capaces de observar \(C\) junto con el valor de \(\delta\). Cuando \(X\leq C\) entonces somos capaces de observar la variable de interés y además el valor de \(\delta\).
En resumen, en lugar de observar la muestra \(\left( X_1, X_2, \ldots, X_n \right)\), sólo podemos observar \[\left( \left( T_1, \delta _1 \right), \left( T_2, \delta _2 \right), \ldots ,\left( T_n, \delta_n \right) \right),\] siendo \(T_i=\min \left\{ X_i,C_i\right\}\) los tiempos de vida observados y \[\delta _i=\mathbf{1}_{\left\{ X_i\leq C_i\right\} }=\mathbf{1}_{\left\{ T_i=X_i\right\} }\] los indicadores de censura, para \(i=1,2,\ldots ,n\). En el modelo de censura aleatoria por la derecha, que es el más habitual, se supone que \(X_i\) y \(C_i\) (\(i=1,2,\ldots ,n\)) son independientes. Además \(\left( X_1, X_2, \ldots ,X_n \right)\) son mutuamente independientes, como también lo son \(\left( C_1, C_2,\ldots ,C_n \right)\).
Denotando por \(F\) (respectivamente \(G\) y \(H\)) la función de distribución de la variable aleatoria \(X\) (respectivamente \(C\) y \(T\)), la condición de independencia implica que \[1-H\left( t \right) =\left( 1-F\left( t \right) \right) \left( 1-G\left( t \right) \right).\]
8.1.1 Estimador de Kaplan-Meier
Puede verse fácilmente que, bajo censura aleatoria por la derecha, la distribución empírica \(F_n\left( t \right) =\frac{1}{n} \sum_{i=1}^{n}\mathbf{1}_{\left\{ T_i\leq t\right\} }\) deja de ser consistente. En este contexto el estimador no paramétrico de máxima verosimilitud de la función de distribución es el estimador límite-producto, propuesto por Kaplan y Meier (1958), obtenido a partir de la función de supervivencia (\(S\left( t \right) = 1-F\left( t \right)\)): \[\hat{S}\left( t \right) = 1-\hat{F}\left( t \right) = \prod_{T_{(i)}\leq t}\left( \frac{n-i}{n-i+1} \right)^{\delta _{(i)}},\] siendo \(\left( T_{(1)},T_{\left( 2 \right)},\ldots ,T_{\left( n \right)} \right)\) la muestra de estadísticos ordenados de los tiempos de vida observados y \(\left( \delta _{(1)},\delta _{\left(2 \right)}, \ldots ,\delta _{(n)} \right)\) los correspondientes concomitantes.
Ejemplo 8.1 (Estimación de Kaplan-Meier)
Se observan los datos censurados: \(\left( 2.1,0 \right)\), \(\left(3.2,1 \right)\), \(\left( 1.2,1 \right)\), \(\left( 4.3,0 \right)\), \(\left( 1.8,1 \right)\), \(\left( 3.9,1 \right)\), \(\left( 2.7,0 \right)\), \(\left( 2.5,1 \right)\). El estimador resulta:
\[\hat{F}\left( t \right) =\left\{ \begin{array}{ll} 0& \text{si } t<1.2 \\ 0.125& \text{si } 1.2\leq t<1.8 \\ 0.25& \text{si } 1.8\leq t<2.5 \\ 0.4& \text{si } 2.5\leq t<3.2 \\ 0.6& \text{si } 3.2\leq t<3.9 \\ 0.8& \text{si } 3.9\leq t \end{array} \right.\]
En R se recomienda emplear el paquete survival para el análisis de
datos censurados. Podemos utilizar la función survfit() para obtener
la estimación Kaplan-Meier de la función de supervivencia
(y a partir de ella la de la distribución).
En este caso podríamos utilizar el siguiente código :
datcen <- data.frame(t = c(2.1, 3.2, 1.2, 4.3, 1.8, 3.9, 2.7, 2.5),
cen = c(0, 1, 1, 0, 1, 1, 0, 1))
library(survival)
fit <- survfit(Surv(t, cen)~1, data = datcen)
summary(fit)## Call: survfit(formula = Surv(t, cen) ~ 1, data = datcen)
##
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 1.2 8 1 0.875 0.117 0.6734 1
## 1.8 7 1 0.750 0.153 0.5027 1
## 2.5 5 1 0.600 0.182 0.3315 1
## 3.2 3 1 0.400 0.203 0.1477 1
## 3.9 2 1 0.200 0.174 0.0363 1old.par <- par(mfrow = c(1, 2))
plot(fit, main = "Método plot de un objeto 'survfit'")
legend("bottomleft", c("supervivencia", "conf.int"), lty = 1:2)
with(fit, {
plot(c(0, time), c(1, surv), type = "s", lty = 2,
main = "Estimaciones funciones supervicencia y distribución",
xlab = "t", ylab = "", ylim = c(0, 1))
lines(c(0, time), 1 - c(1, surv), type = "s")
legend("bottomright", c("supervivencia", "distribución"), lty = 2:1)
})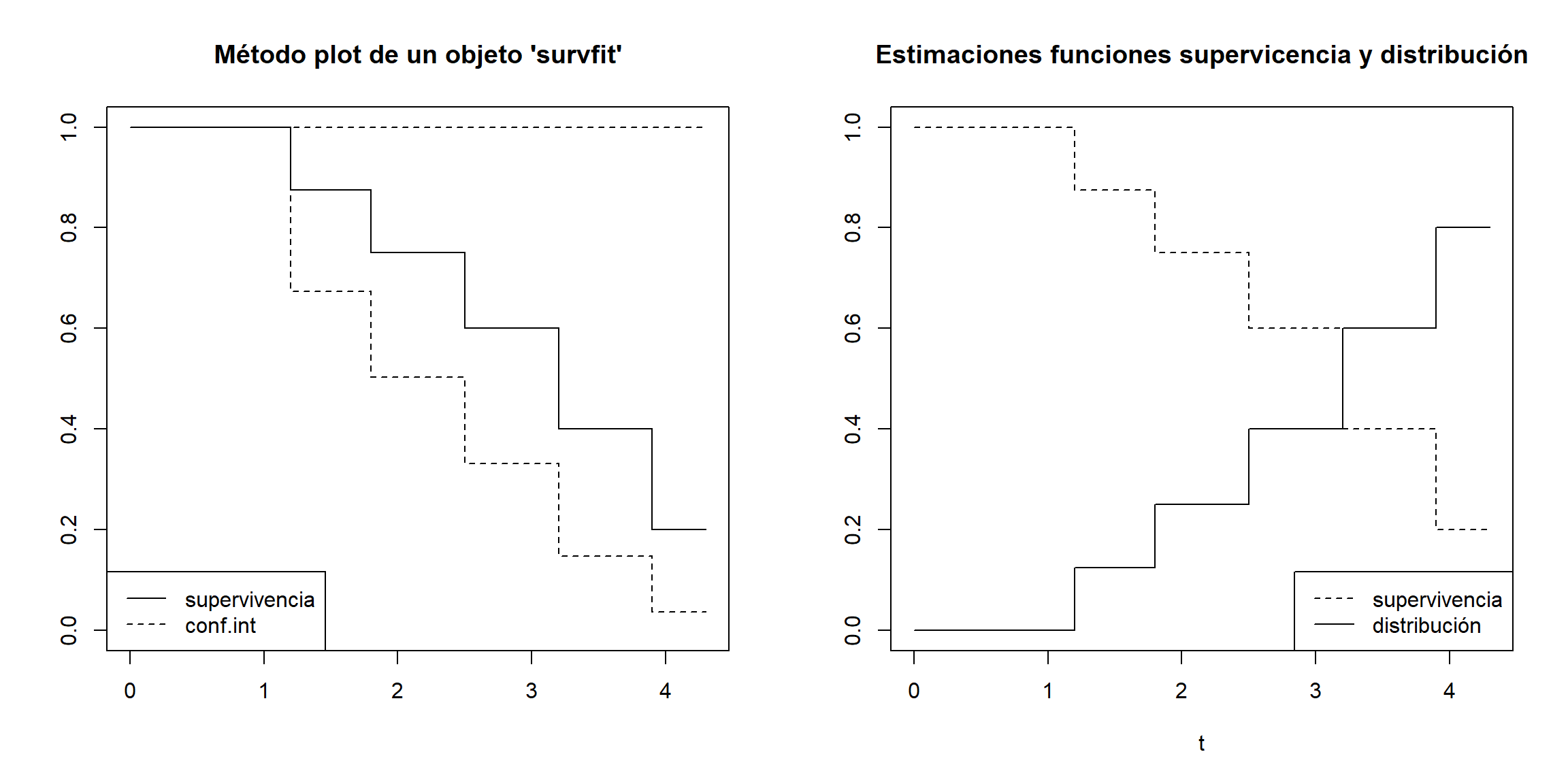
Figura 8.1: Estimaciones Kaplan-Meier de la función de supervivencia y de la función de distribución.
par(old.par)8.1.2 Distribución asintótica del estimador de Kaplan-Meier
El estimador de Kaplan-Meier sólo otorga pesos positivos a los datos no censurados, aunque la forma de distribuirse los datos censurados en medio de los no censurados afecta a los pesos de estos últimos. Por otra parte, en ausencia de censura (es decir \(\delta _i=1\), \(i=1,2,\ldots ,n\)), el estimador de Kaplan-Meier coincide con la distribución empírica.
La obtención de la propiedades de sesgo y varianza asintóticos y distribución límite del estimador de Kaplan-Meier es mucho más laboriosa que en el caso de la distribución empírica, en un contexto sin censura. Esto es así porque el estimador de Kaplan-Meier deja de ser una suma de variables iid, como sí ocurre con la empírica.
Breslow y Crowley (1974) obtienen el siguiente resultado para la distribución límite para el estimador de Kaplan-Meier: \[\sqrt{n}\left( \hat{F}\left( t \right) -F\left( t \right) \right) \overset{d}{\longrightarrow} \mathcal{N}\left( 0,\sigma^2\left( t \right) \right),\] siendo \[\begin{aligned} \sigma^2\left( t \right) &= \left( 1-F\left( t \right) \right) ^2\int_{0}^{t}\frac{dH_1\left( u \right)}{\left( 1-H\left( u \right) \right)^2}\text{, }t\leq H^{-1}(1) , \\ H_1\left( u \right) &= P\left( X\leq u,X\leq C \right) =P\left( T\leq u,\delta =1 \right). \end{aligned}\] También existen resultados de convergencia en distribución del proceso estocástico \[\left\{ \sqrt{n}\left( \hat{F}\left( t \right) - F\left( t \right) \right) : t \in \left[ 0,H^{-1}(1) \right] \right\}\] a un proceso gaussiano límite.