8.4 Implementación en R (con los paquetes boot y survival)

La función censboot() del paquete boot implementa distintos métodos de remuestreo para datos censurados. Por defecto utiliza el bootstrap simple (sim = "ordinary") y su uso es prácticamente igual al del bootstrap uniforme con la función boot() (descrita en la Sección 1.4.1), la única diferencia es que la función statistic solo tiene los datos como único parámetro (aunque en este caso podríamos emplear también la función boot()).

8.4.1 Bootstrap simple

Como ejemplo utilizaremos el conjunto de datos channing del paquete boot, que contiene la edad de entrada y de partida o muerte de las personas que pasaron por el centro de retiro ‘Channing House’ (Palo Alto, California), desde su apertura en 1964 hasta el 1 de julio de 1975 (ver Sección 3.5 y ‘Practical 3.2,’ de Davison y Hinkley, 1997). En primer lugar consideraremos únicamente la muestra de hombres:

# Datos
library(boot)
data(channing)
# Calcular edad (de partida o muerte) en años
channing$age <- (channing$entry + channing$time)/12
# Seleccionar hombres (y de paso hacer que `index = c(1, 2)` para `censboot()`)
chan <- subset(channing, sex=="Male", c(age, cens))

# Estimación supervivencia
library(survival)
chan.F <- survfit(Surv(age, cens)~1, data = chan)
chan.F

## Call: survfit(formula = Surv(age, cens) ~ 1, data = chan)
## 
##       n  events  median 0.95LCL 0.95UCL 
##    97.0    46.0    87.0    85.8    90.4

# plot(chan.F)
# Estimaciones de interés
with(chan.F, 
    c(s75 = max(surv[time > 75]), s85 = max(surv[time > 85]),
      p75 = min(time[surv <= 0.75]), p50 = min(time[surv <= 0.5])) 
)

##        s75        s85        p75        p50 
##  0.9160745  0.6347541 82.4166667 87.0000000

# Bootstrap
# library(boot)
chan.stat <- function(data) {
    s <- survfit(Surv(age, cens)~1, data = data)
    with(s, c(s75 = max(surv[time > 75]), s85 = max(surv[time > 85]),
            p75 = min(time[surv <= 0.75]), p50 = min(time[surv <= 0.5])))
}
set.seed(1)
chan.boot <- censboot(chan, chan.stat, R = 199) # sim = "ordinary"
chan.boot

## 
## CASE RESAMPLING BOOTSTRAP FOR CENSORED DATA
## 
## 
## Call:
## censboot(data = chan, statistic = chan.stat, R = 199)
## 
## 
## Bootstrap Statistics :
##       original       bias    std. error
## t1*  0.9160745 -0.006995081  0.03133656
## t2*  0.6347541 -0.003538939  0.05595748
## t3* 82.4166667 -0.040619765  1.22517032
## t4* 87.0000000  0.195142379  1.07267425

8.4.2 Otros métodos de remuestreo

La función censboot() implementa otros dos métodos de remuestreo, sim = c("cond", "weird"), aunque en ambos casos hay que establecer en el parámetro F.surv la estimación de Kaplan-Meier de la supervivencia y, si sim = "cond", la correspondiente a la variable censurante en G.surv. Se recomienda estimarlas con la función survfit() del paquete survival (ver Figura 8.2):

# Estimación supervivencia variable censurante
chan.G <- survfit(Surv(age, 1-cens)~1, data = chan)
# Representación
old.par <- par(mfrow = c(1, 2))
plot(chan.F, main = "Supervivencia (edad)", mark.time = TRUE, 
    xlim = c(60, 100))
plot(chan.G, main = "Supervivencia variable censurante (partida)", 
     mark.time = TRUE, xlim = c(60, 100))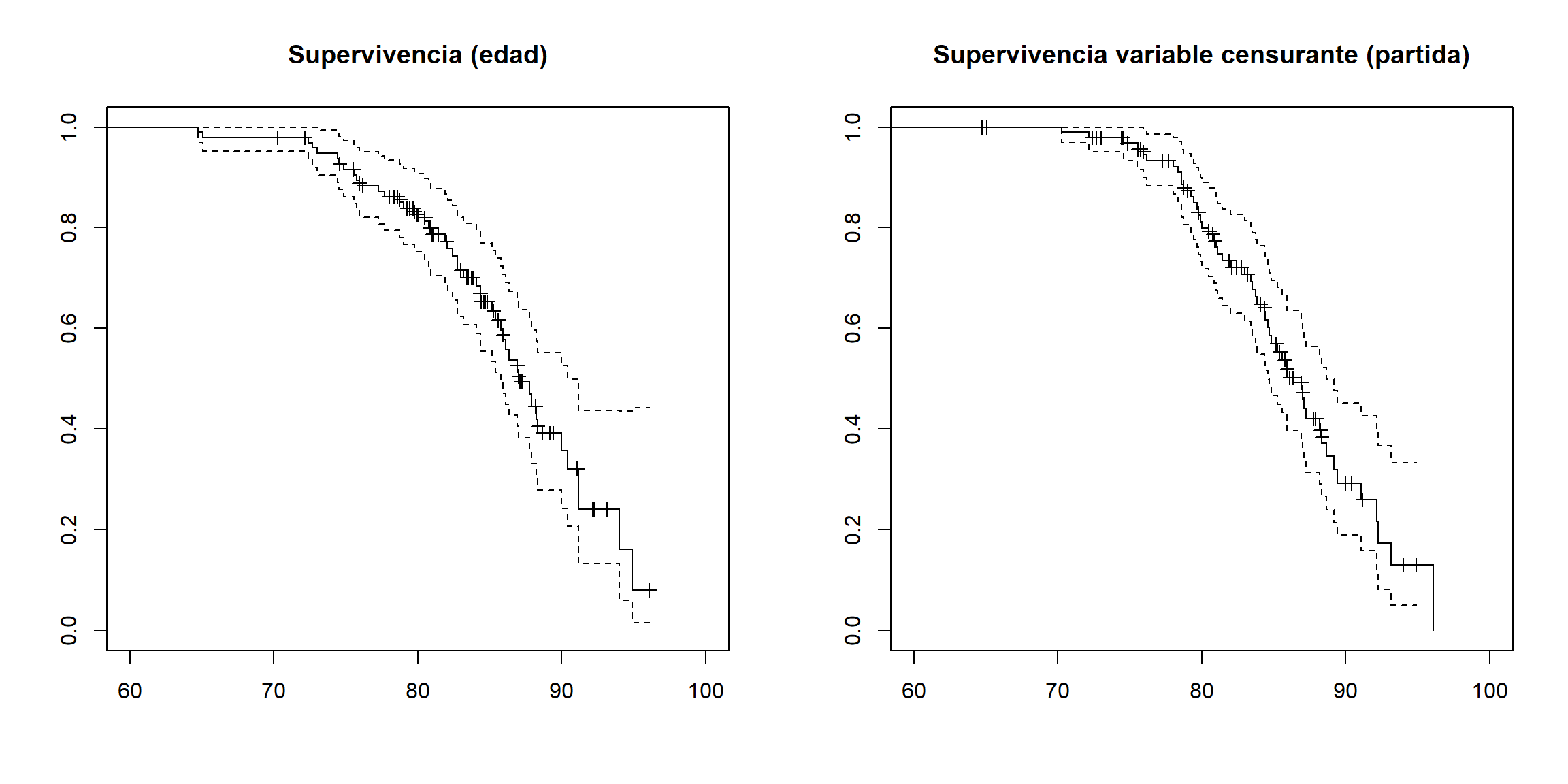

Figura 8.2: Estimaciones de la supervivencia (izquierda; indicando los tiempos de las observaciones censuradas) y de la variable censurante (derecha; indicando los de las no censuradas).

par(old.par)

En el boostrap condicional (sim = "cond") se condiciona el muestreo al patrón de censura observado (en lugar de fijarlo a \(\mathbf{1}\) como en el bootstrap de Reid; Sección 8.3.2). El mecanismo es similar al del bootstrap obvio (Sección 8.2.2):

1. Construir los estimadores de Kaplan-Meier de las distribuciones de la variable de interés, \(\hat{F}\left( t \right)\), y de la variable censurante, \(\hat{G}\left( t \right)\).

2. Para cada índice \(i=1,2,\ldots ,n\), generar \(X_i^{\ast}\) independientes con distribución \(\hat{F}\).

3. Si la \(i\)-ésima observación está censurada (\(\delta_i=0\)) se toma \(C_i^{\ast}=T_i\) y si no (\(\delta_i=1\)) se genera un valor de la estimación de la distribución de la variable censurante condicionada a \(C > T_i\): \[\hat G \left(\left. t \ \right\vert_{\ t > T_i} \right) = \frac{\hat G(t) - \hat G(T_i)}{1- \hat G(T_i)}.\]

4. Definir \(T_i^{\ast}=\min \left\{ X_i^{\ast},C_i^{\ast}\right\}\) y \(\delta_i^{\ast}=\mathbf{1}_{\left\{ X_i^{\ast}\leq C_i^{\ast}\right\}}\), para \(i = 1, 2, \ldots, n\), y considerar la remuestra bootstrap \(\left( \mathbf{T}^{\ast},\boldsymbol{\delta}^{\ast}\right)\), con \(\mathbf{T}^{\ast}=\left( T_1^{\ast},T_2^{\ast}, \ldots, T_n^{\ast} \right)\) y \(\boldsymbol{\delta}^{\ast} = \left( \delta_1^{\ast}, \delta_2^{\ast},\ldots ,\delta_n^{\ast} \right)\).

El otro método (sim = "weird") es el denominado weird bootstrap (Andersen et al., 1993) que emplea la estimación de Nelson-Aalen de la función de riesgo acumulada para generar los valores (e.g. Sección 3.5.2 de Davison y Hinkley, 1997).

El siguiente código muestra un ejemplo de la aplicación de ambos métodos:

chan.boot2 <- censboot(chan, chan.stat, R = 199, F.surv = chan.F, 
                  G.surv = chan.G, sim = "cond")
chan.boot2

## 
## CONDITIONAL BOOTSTRAP FOR CENSORED DATA
## 
## 
## Call:
## censboot(data = chan, statistic = chan.stat, R = 199, F.surv = chan.F, 
##     G.surv = chan.G, sim = "cond")
## 
## 
## Bootstrap Statistics :
##       original       bias    std. error
## t1*  0.9160745  0.002340590  0.02796666
## t2*  0.6347541 -0.001057025  0.05382609
## t3* 82.4166667  0.019681742  1.21793756
## t4* 87.0000000  0.286013400  0.95041994

chan.boot3 <- censboot(chan, chan.stat, R = 199, F.surv = chan.F, 
                  sim = "weird")
chan.boot3

## 
## WEIRD BOOTSTRAP FOR CENSORED DATA
## 
## 
## Call:
## censboot(data = chan, statistic = chan.stat, R = 199, F.surv = chan.F, 
##     sim = "weird")
## 
## 
## Bootstrap Statistics :
##       original        bias    std. error
## t1*  0.9160745 -4.082326e-05  0.02825475
## t2*  0.6347541  1.639197e-03  0.05086460
## t3* 82.4166667  2.303183e-02  1.14079354
## t4* 87.0000000  2.458124e-01  0.96511648