1.4 Herramientas disponibles en R sobre bootstrap

En R hay una gran cantidad de paquetes que implementan métodos bootstrap. Por ejemplo, al ejecutar el comando ??bootstrap (o help.search('bootstrap')) se mostrarán las funciones de los paquetes instalados que incluyen este término en su documentación (se puede realizar la búsqueda en todos los paquetes disponibles de R a través de https://www.rdocumentation.org).

De entre todos estas herramientas destacan dos librerías como las más empleadas:

  • bootstrap: contiene las rutinas (bootstrap, cross-validation, jackknife) y los datos del libro “An Introduction to the Bootstrap” de B. Efron y R. Tibshirani, 1993, Chapman and Hall. La librería fue desarrollada originalmente en S por Rob Tibshirani y exportada a R por Friedrich Leisch. Es útil para desarrollar los ejemplos que se citan en ese libro.

  • boot: incluye las funciones y conjuntos de datos utilizados en el libro “Bootstrap Methods and Their Applications” de A. C. Davison y D. V. Hinkley, 1997, Cambridge University Press. Esta librería fue desarrollada originalmente en S por Angelo J. Canty y posteriormente exportada a R (ver Canty, 2002). Este paquete es mucho más completo que el paquete bootstrap, forma parte de la distribución estándar de R y es el que emplearemos como referencia en este libro (ver Sección 1.4.1).

Por otra parte existen numerosas rutinas (scripts) realizadas en R por diversos autores, que están disponibles en Internet (por ejemplo, puede ser interesante realizar una búsqueda en https://rseek.org).

El bootstrap uniforme se puede implementar fácilmente. Por ejemplo, una rutina general para el caso univariante sería la siguiente:

#' @param x vector que contiene la muestra.
#' @param B número de réplicas bootstrap.
#' @param statistic función que calcula el estadístico.
boot.strap0 <- function(x, B=1000, statistic=mean){
  ndat <- length(x)
  x.boot <- sample(x, ndat*B, replace=TRUE)
  x.boot <- matrix(x.boot, ncol=B, nrow=ndat)
  stat.boot <- apply(x.boot, 2, statistic)
}

Podríamos aplicar esta función a la muestra de tiempos de vida de microorganismos con el siguiente código:

fstatistic <- function(x){
  #  mean(x)
  #  mean(x, trim=0.2)
  median(x)
  #  max(x)
}

B <- 1000
set.seed(1)
stat.dat <- fstatistic(muestra)
stat.boot <- boot.strap0(muestra, B, fstatistic)

res.boot <- c(stat.dat, mean(stat.boot)-stat.dat, sd(stat.boot))
names(res.boot) <- c("Estadístico", "Sesgo", "Error Std.")
res.boot
## Estadístico       Sesgo  Error Std. 
##   0.6110000   0.0609260   0.2481362

La función boot.strap0() anterior no es adecuada para el caso multivariante (por ejemplo cuando estamos interesados en regresión). Como se mostró en la Sección 1.1.3 sería preferible emplear remuestras del vector de índices. Por ejemplo:

#' @param datos vector, matriz o data.frame que contiene los datos.
#' @param B número de réplicas bootstrap.
#' @param statistic función con al menos dos parámetros, 
#' los datos y el vector de índices de remuestreo, 
#' y que devuelve el vector de estadísticos.
#' @param ... parámetros adicionales de la función statistic.
boot.strap <- function(datos, B=1000, statistic, ...) {
  ndat <- NROW(datos)
  i.boot <- sample(ndat, ndat*B, replace=TRUE)
  i.boot <- matrix(i.boot, ncol=B, nrow=ndat)
  stat.boot <- drop(apply(i.boot, 2, function(i) statistic(datos, i, ...)))
}

El paquete boot, descrito a continuación, emplea una implementación similar.

1.4.1 El paquete boot

La función principal de este paquete es la función boot() que implementa distintos métodos de remuestreo para datos i.i.d.. En su forma más simple permite realizar bootstrap uniforme (que en la práctica también se denomina habitualmente bootstrap noparamétrico):

boot(data, statistic, R)

donde data es un vector, matriz o data.frame que contiene los datos, R es el número de réplicas bootstrap, y statistic es una función con al menos dos parámetros (con las opciones por defecto), los datos y el vector de índices de remuestreo, y que devuelve el vector de estadísticos.

Por ejemplo, para hacer inferencia sobre la mediana del tiempo de microorganismos, podríamos emplear el siguiente código:

library(boot)
muestra <- c(0.143, 0.182, 0.256, 0.26, 0.27, 0.437, 0.509, 
             0.611, 0.712, 1.04, 1.09, 1.15, 1.46, 1.88, 2.08)

statistic <- function(data, i){
  # remuestra <- data[i]; median(remuestra)
  median(data[i])
}

set.seed(1)
res.boot <- boot(muestra, statistic, R = 1000)

El resultado que devuelve esta función es un objeto de clase boot, una lista con los siguientes componentes:

names(res.boot)
##  [1] "t0"        "t"         "R"         "data"      "seed"      "statistic"
##  [7] "sim"       "call"      "stype"     "strata"    "weights"

Además de los parámetros de entrada (incluyendo los valores por defecto), contiene tres componentes adicionales:

  • tO: el valor observado del estadístico (su evaluación en los datos originales).

  • t: la matriz de réplicas bootstrap del estadístico (cada fila se corresponde con una remuestra).

  • seed: el valor inicial de la semilla (.Random.seed) empleada para la generación de las réplicas.

Este tipo de objetos dispone de dos métodos principales: el método print() que muestra un resumen de los resultados (incluyendo aproximaciones bootstrap del sesgo y del error estándar de los estadísticos; ver Capítulo 2):

res.boot
## 
## ORDINARY NONPARAMETRIC BOOTSTRAP
## 
## 
## Call:
## boot(data = muestra, statistic = statistic, R = 1000)
## 
## 
## Bootstrap Statistics :
##     original   bias    std. error
## t1*    0.611 0.058523   0.2526519

y el método plot() que genera gráficas básicas de diagnosis de los resultados (correspondientes al estadístico determinado por el parámetro index, por defecto = 1):

plot(res.boot)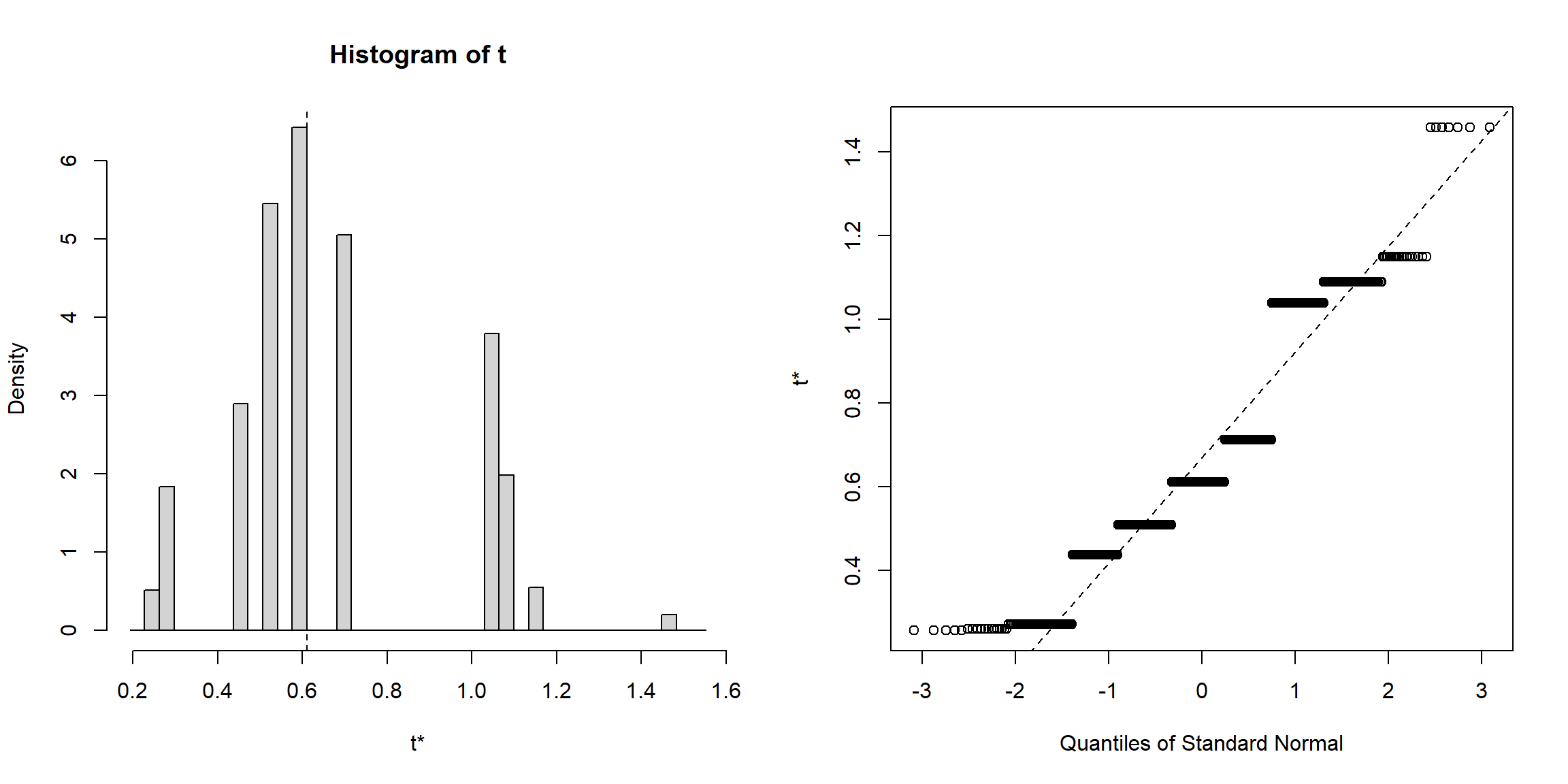
Gráficos de diagnóstico de los resultados bootstrap de la mediana de los tiempos de vida de microorganismos.

Figura 1.5: Gráficos de diagnóstico de los resultados bootstrap de la mediana de los tiempos de vida de microorganismos.

Es recomendable examinar la distribución bootstrap del estimador (o estadístico) para detectar posibles problemas. Como en este caso puede ocurrir que el estadístico bootstrap tome pocos valores distintos, lo que indicaría que el número de réplicas bootstrap es insuficiente o que hay algún problema con método de remuestreo empleado (en este caso la distribución objetivo es continua). Se darán más detalles sobre los posibles problemas del bootstrap uniforme en la Sección 3.5.

Además de estos métodos, las principales funciones de interés serían:

  • jack.after.boot(): genera un gráfico para diagnósticar la inluencia de las observaciones individuales en los resultados bootstrap (se representan los cuantiles frente a las diferencias en el estadístico al eliminar una observación; este gráfico también se puede obtener estableciendo jack = TRUE en plot.boot()).

  • boot.array(): genera la matriz de índices a partir de la que se obtuvieron las remuestras (permite reconstruir las remuestras bootstrap).

  • boot.ci(): construye distintos tipos de intervalos de confianza (se tratarán en el Capítulo 4) dependiendo del parámetro type:

    • "norm": utiliza la distribución asintótica normal considerando las aproximaciones bootstrap del sesgo y de la varianza.

    • "basic": emplea el estadístico \(R = \hat \theta - \theta\) para la construcción del intervalo de confianza.

    • "stud": calcula el intervalo a partir del estadístico estudentizado \(R = \left( \hat \theta - \theta \right) / \sqrt{Var(\hat \theta)}\).

    • "perc": utiliza directamente la distribución bootstrap del estadístico (\(R = \hat \theta\)).

    • "bca": emplea el método \(BCa\) (“bias-corrected and accelerated”) propuesto por Efron (1987) (ver Sección 5.3.2 de Davison y Hinkley, 1997).

    • "all": calcula los cinco tipos de intervalos anteriores.

Como ya se comentó, la función boot() admite estadísticos multivariantes (haciendo que la función statistic devuelva un vector en lugar de un escalar), pero por defecto las funciones anteriores consideran el primer componente como el estadístico principal. Para obtener resultados de otros componentes del vector de estadísticos habrá que establecer el parámetro index igual al índice deseado. Además, en algunos casos (por ejemplo para la obtención de intevalos de confianza estudentizados con la función boot.ci()) se supone, por defecto, que el segundo componente del vector de estadísticos contiene estimaciones de la varianza del estadístico para cada réplica boostrap.

Ejemplo 1.6 (Inferencia sobre la media con varianza desconocida, continuación)

Continuando con el Ejemplo 1.5 de inferencia sobre la media con varianza desconocida. Para obtener la estimación por intervalo de confianza del tiempo de vida medio de los microorganismos con el paquete boot, podríamos emplear el siguiente código: 
library(boot)
muestra <- c(0.143, 0.182, 0.256, 0.26, 0.27, 0.437, 0.509, 
             0.611, 0.712, 1.04, 1.09, 1.15, 1.46, 1.88, 2.08)

statistic <- function(data, i){
  remuestra <- data[i]
  c(mean(remuestra), var(remuestra)/length(remuestra))
}

set.seed(1)
res.boot <- boot(muestra, statistic, R = 1000)
res.boot
## 
## ORDINARY NONPARAMETRIC BOOTSTRAP
## 
## 
## Call:
## boot(data = muestra, statistic = statistic, R = 1000)
## 
## 
## Bootstrap Statistics :
##      original       bias    std. error
## t1* 0.8053333  0.003173267 0.158330646
## t2* 0.0259338 -0.002155755 0.007594682
boot.ci(res.boot)
## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = res.boot)
## 
## Intervals : 
## Level      Normal              Basic             Studentized     
## 95%   ( 0.4918,  1.1125 )   ( 0.4825,  1.0980 )   ( 0.4715,  1.2320 )  
## 
## Level     Percentile            BCa          
## 95%   ( 0.5127,  1.1282 )   ( 0.5384,  1.1543 )  
## Calculations and Intervals on Original Scale

El intervalo marcado como Studentized se obtuvo empleando el mismo estadístico del Ejemplo 1.5.

Modificaciones del bootstrap uniforme

Establecenciendo parámetros adicionales de la función boot se pueden llevar a cabo modificaciones del bootstrap uniforme. Algunos de estos parámetros son los siguientes:

  • strata: permite realizar remuestreo estratificado estableciendo este parámetro como un vector numérico o factor que defina los grupos.

  • sim = c("ordinary" , "parametric", "balanced", "permutation", "antithetic"): permite establecer distintos tipos de remuestreo. Por defecto es igual a "ordinary" que se corresponde con el bootstrap uniforme, descrito anteriormente. Entre el resto de opciones destacaríamos sim = "permutation", que permite realizar contrastes de permutaciones (remuestreo sin reemplazamiento), y sim = "parametric", que permite realizar bootstrap paramétrico (Sección 3.1). En este último caso también habrá que establecer los parámetros ran.gen y mle, y la función statistics no empleará el segundo parámetro de índices.

  • ran.gen: función que genera los datos. El primer argumento será el conjunto de datos original y el segundo un vector de parámetros adicionales (normalmente los valores de los parámetros de la distribución).

  • mle: parámetros de la distribución (típicamente estimados por máxima verosimilitud) o parámetros adicionales para ran.gen ó statistics.

Además hay otros parámetros para el procesamiento en paralelo: parallel = c("no", "multicore", "snow"), ncpus, cl. En el Apéndice B se incluye una pequeña introducción al procesamiento en paralelo y se muestran algunos ejemplos sobre el uso de estos parámetros. También se puede consultar la ayuda de la función boot() (?boot).

El paquete boot también incluye otras funciones que implementan métodos boostrap para otros tipos de datos, como la función censboot() para datos censurados (Capítulo 8) o la función tsboot() para series de tiempo (Capítulo 9).

Finalmente destacar que hay numerosas extensiones implementadas en otros paquetes utilizando el paquete boot (ver Reverse dependencies en la web de CRAN). Por ejemplo en la Sección 3.7 se ilustrará el uso de la función Boot() del paquete car para hacer inferencia sobre modelos de regresión.

1.4.2 Ejemplo: Bootstrap uniforme multidimensional

Como ya se mostró en las Secciones 1.1.3 y 1.4 podemos implementar el bootstrap uniforme en el caso multidimensional (denominado también remuestreo de casos o bootstrap de las observaciones) de modo análogo al unidimensional.

Consideraremos como ejemplo el conjunto de datos Prestige del paquete carData, y supongamos que queremos realizar inferencias sobre el coeficiente de correlación entre prestige (puntuación de ocupaciones obtenidas a partir de una encuesta) eincome (media de ingresos en la ocupación).

data(Prestige, package = "carData")
str(Prestige)
## 'data.frame':    102 obs. of  6 variables:
##  $ education: num  13.1 12.3 12.8 11.4 14.6 ...
##  $ income   : int  12351 25879 9271 8865 8403 11030 8258 14163 11377 11023 ...
##  $ women    : num  11.16 4.02 15.7 9.11 11.68 ...
##  $ prestige : num  68.8 69.1 63.4 56.8 73.5 77.6 72.6 78.1 73.1 68.8 ...
##  $ census   : int  1113 1130 1171 1175 2111 2113 2133 2141 2143 2153 ...
##  $ type     : Factor w/ 3 levels "bc","prof","wc": 2 2 2 2 2 2 2 2 2 2 ...
# with(Prestige, cor(income, prestige))
cor(Prestige$income, Prestige$prestige)
## [1] 0.7149057

En el siguiente código se emplea el paquete boot para realizar bootstrap uniforme multidimensional sobre este estadístico:

library(boot)

statistic <- function(data, i){
  remuestra <- data[i, ]
  cor(remuestra$income, remuestra$prestige)
}

set.seed(1)
B <- 1000
res.boot <- boot(Prestige, statistic, R = B)
res.boot
## 
## ORDINARY NONPARAMETRIC BOOTSTRAP
## 
## 
## Call:
## boot(data = Prestige, statistic = statistic, R = B)
## 
## 
## Bootstrap Statistics :
##      original      bias    std. error
## t1* 0.7149057 0.006306905  0.04406473
plot(res.boot)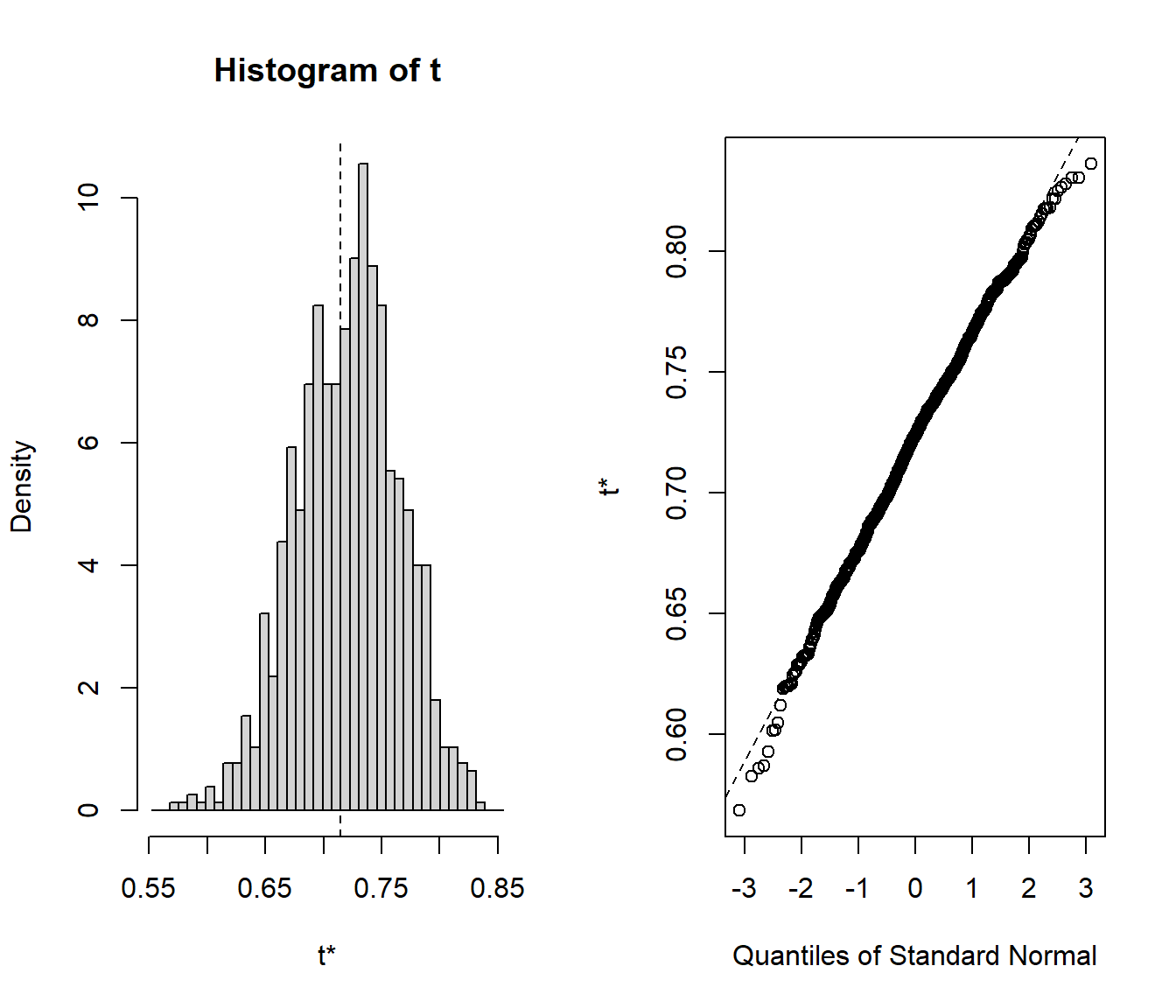

En este caso podemos observar que la distribución bootstrap del estimador es asimétrica, por lo que asumir que su distribución es normal podría no ser adecuado (por ejemplo para la construcción de intervalos de confianza, que se tratarán en la Sección 4.6.3).

Como comentario final, nótese que en principio el paquete boot está diseñado para obtener réplicas bootstrap de un estimador, por lo que si lo que nos interesa es emplear otro estadístico habría que construirlo a partir de ellas (como hacen otras funciones secundarias como boot.ci()). Por ejemplo, si queremos emplear el estadístico \(R = \hat \theta - \theta\) (bootstrap percentil básico o natural), podemos obtener la correspondiente distribución bootstrap (aproximada por Monte Carlo) con el siguiente código:

estadistico_boot <- res.boot$t - res.boot$t0 
hist(estadistico_boot)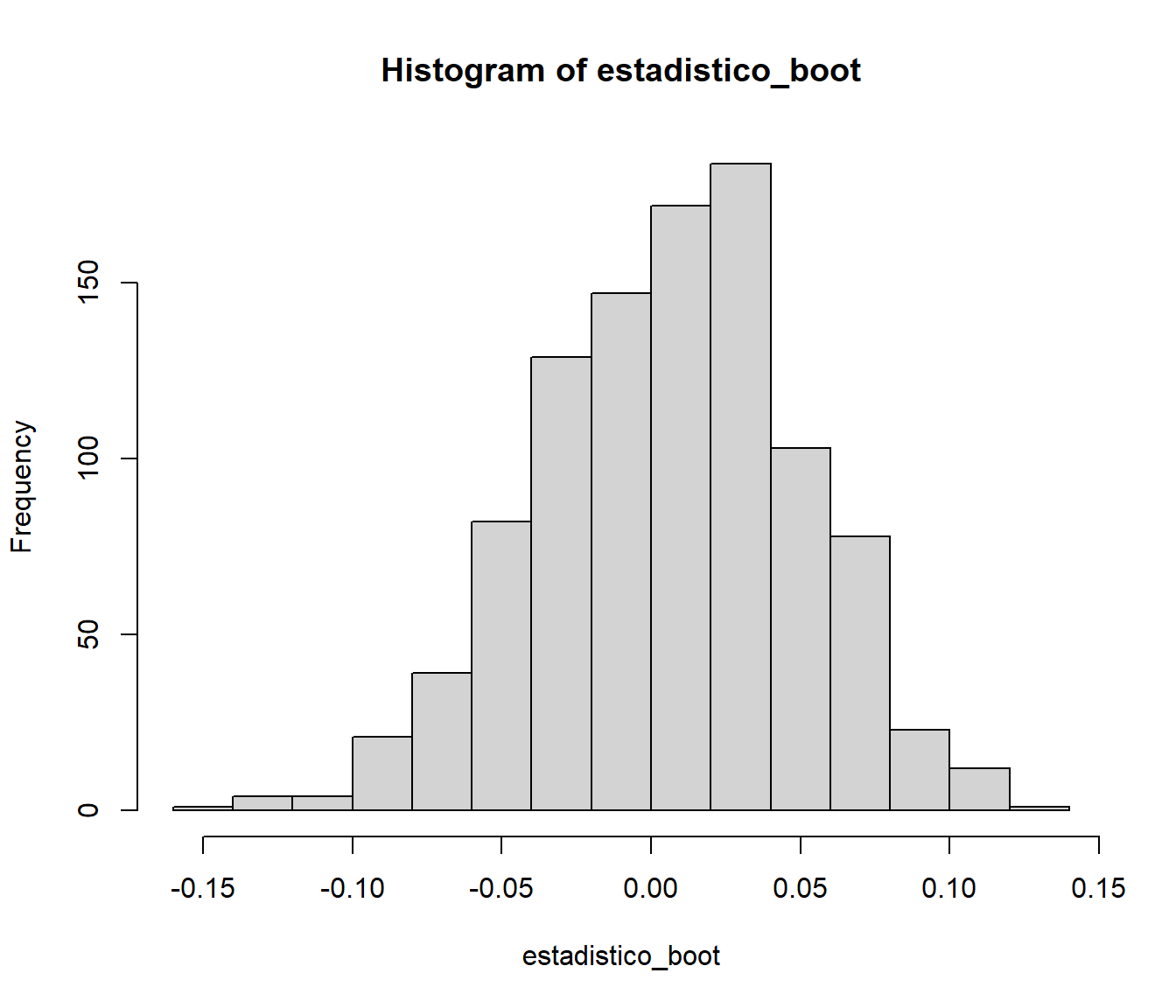

A partir de la distribución empírica del estadístico bootstrap \(R^{\ast} = \hat \theta^{\ast} - \hat \theta\) aproximaríamos la característica de interés de la distribución en el muestreo de \(R = \hat \theta - \theta\). Por ejemplo, para aproximar \(\psi \left( u \right) =P\left( R\leq u \right)\) emplearíamos la frecuencia relativa: \[\hat{\psi}_{B}\left( u \right) = \frac{1}{B}\sum_{i=1}^{B}\mathbf{1}\left\{ R^{\ast (i)}\leq u\right\}.\]

u <- 0
sum(estadistico_boot <= u)/B
## [1] 0.427
# Equivalentemente:
mean(estadistico_boot <= u)
## [1] 0.427