5.3 Método de Alias

Se basa en representar la distribución de \(X\) como una mixtura (uniforme) de variables dicotómicas (Walker, 1977): \[Q^{(i)}=\left\{ \begin{array}{ll} x_{i} & \text{con prob. } q_{i} \\ x_{a_{i}} & \text{con prob. } 1-q_{i} \end{array} \ \right.\]

Hay varias formas de construir las tablas de probabilidades \(q_i\) y de alias \(a_i\). Se suele emplear el denominado algoritmo “Robin Hood” de inicialización (Kronmal y Peterson, 1979). La idea es “tomar prestada” parte de la probabilidad de los valores más probables (ricos) para asignársela a los valores menos probables (pobres), recordando el valor de donde procede (almacenando el índice en \(a_i\)).

Algoritmo 5.4 ("Robin Hood" de inicialización; Kronmal y Peterson, 1979)

  1. Desde \(i=1\) hasta \(n\) hacer \(q_{i}=np_{i}\).

  2. Establecer \(L=\left\{ l:q_{l}<1\right\}\) y \(H=\left\{ h:q_{h}\geq 1\right\}\).

  3. Si \(L\) ó \(H\) vacios terminar.

  4. Seleccionar \(l\in L\) y \(h\in H\).

  5. Hacer \(a_{l}=h\).

  6. Eliminar \(l\) de \(L\).

  7. Hacer \(q_{h}=q_{h}-\left( 1-q_{l}\right)\).

  8. Si \(q_{h}<1\) mover \(h\) de \(H\) a \(L\).

  9. Ir al paso 3.

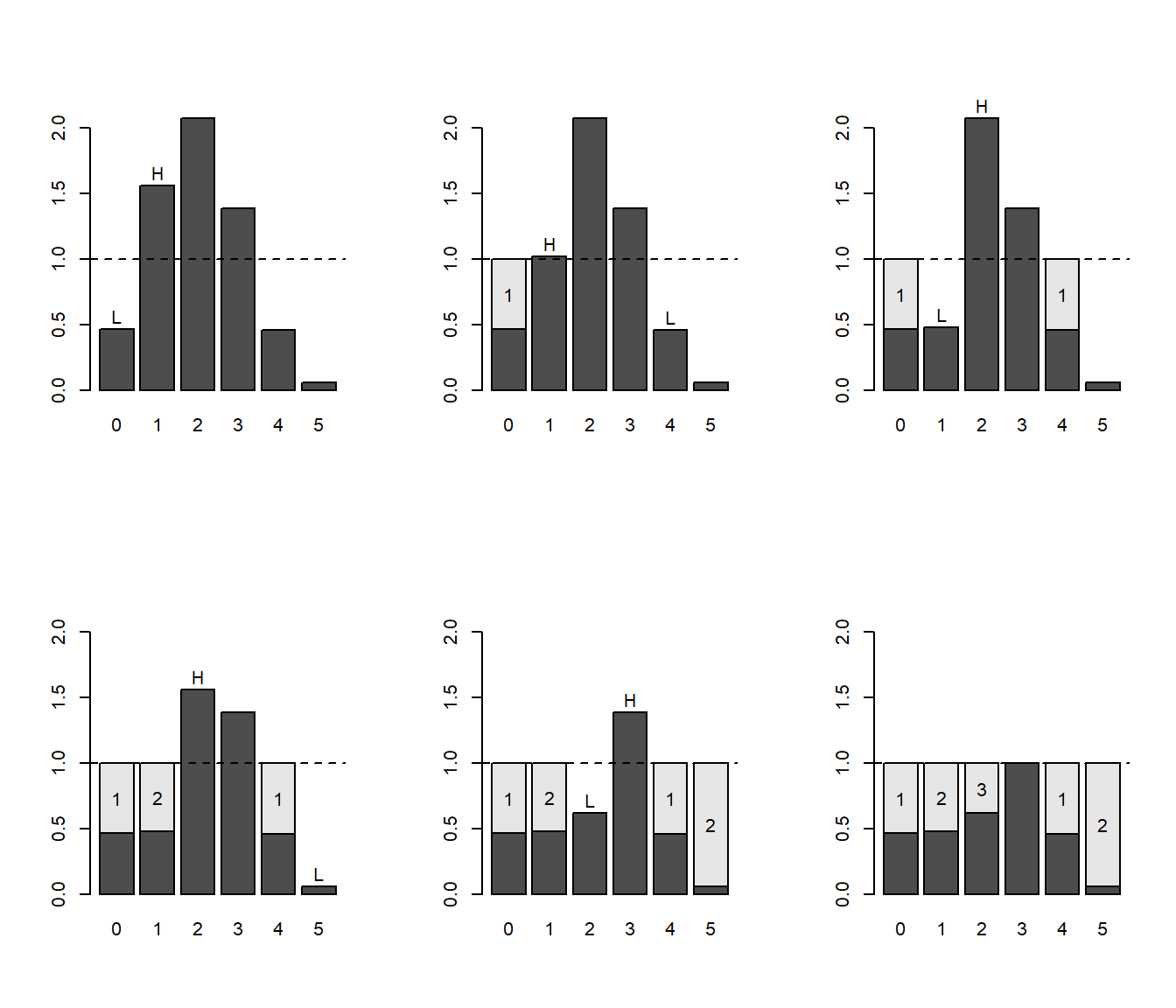
Pasos del algoritmo de inicialización del método Alias.

Figura 5.5: Pasos del algoritmo de inicialización del método Alias.

El algoritmo para generar las simulaciones es el estándar del método de composición:

Algoritmo 5.5 (método alias de simulación; Walker, 1977)

  1. Generar \(U,V\sim \mathcal{U}\left( 0,1\right)\).

  2. Hacer \(i=\left\lfloor nU\right\rfloor +1\).

  3. Si \(V<q_{i}\) devolver \(X=x_{i}\).

  4. En caso contrario devolver \(X=x_{a_{i}}\).

Este algoritmo es muy eficiente y es el empleado en la función sample() de R18.

Este método también está implementado en la función simres::rpmf.alias() (fichero rpmf.R), empleando código R menos eficiente:

rpmf.alias
## function(x, prob = 1/length(x), n = 1000, as.factor = FALSE) {
##   # Inicializar tablas
##   a <- numeric(length(x))
##   q <- prob*length(x)
##   low <- q < 1
##   high <- which(!low)
##   low <- which(low)
##   while (length(high) && length(low)) {
##     l <- low[1]
##     h <- high[1]
##     a[l] <- h
##     q[h] <- q[h] - (1 - q[l])
##     if (q[h] < 1) {
##       high <- high[-1]
##       low[1] <- h
##     } else low <- low[-1]
##   } # while
##   # Generar valores
##   V <- runif(n)
##   i <- floor(runif(n)*length(x)) + 1
##   X <- x[ ifelse( V < q[i], i, a[i]) ]
##   if(as.factor) X <- factor(X, levels = x)
##   return(X)
## }
## <bytecode: 0x00000000389e75f0>
## <environment: namespace:simres>

Ejemplo 5.4 (Simulación de una binomial mediante en método de Alias)

Repetimos la simulación del Ejemplo 5.1 anterior empleando esta rutina.

set.seed(1)
system.time( rx <- rpmf.alias(x, pmf, nsim) )
##    user  system elapsed 
##    0.02    0.00    0.02

Análisis de los resultados:

res <- table(rx)/nsim
plot(res, ylab = "frecuencia relativa", xlab = "valores")
points(x, pmf, pch = 4, col = "blue")  # Comparación teórica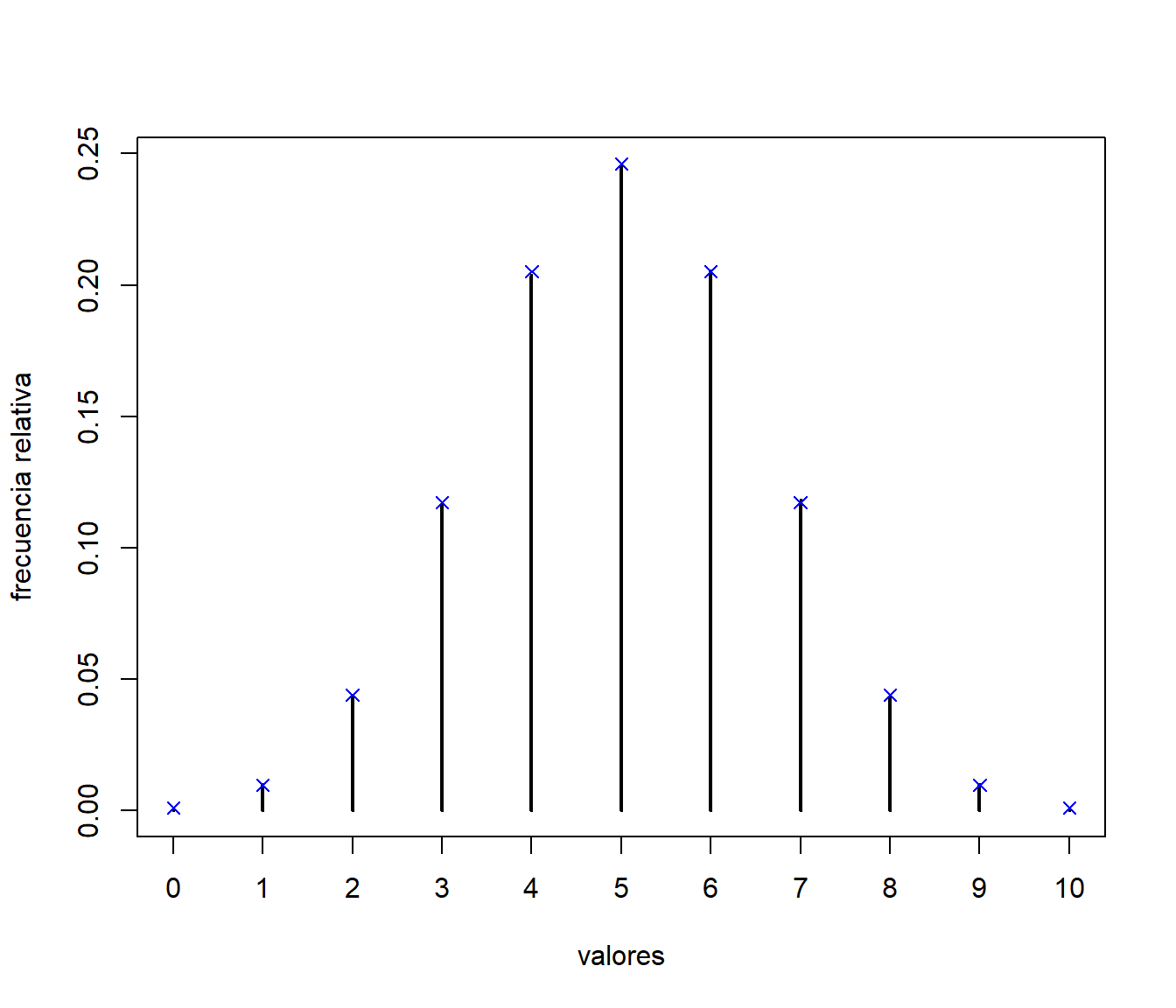
Comparación de las frecuencias relativas de los valores generados, mediante el método de alias, con las probabilidades teóricas.

Figura 5.6: Comparación de las frecuencias relativas de los valores generados, mediante el método de alias, con las probabilidades teóricas.

  1. R implementa este algoritmo en el fichero fuente random.c (para muestreo probabilístico con reemplazamiento, función C walker_ProbSampleReplace()), aunque el paso 2 del algoritmo de simulación empleado por defecto cambió ligeramente a partir de la versión 3.6.0 para evitar posibles problemas de redondeo (ver Sección 1.3.1).↩︎