6.3 Factorización de la matriz de covarianzas

Teniendo en cuenta que si \(Cov(\mathbf{X})= I\), entonces: \[Cov(A\mathbf{X}) = AA^t.\] La idea de este tipo de métodos es simular datos independientes y transformarlos linealmente de modo que el resultado tenga la covarianza deseada \(\Sigma = AA^t\).

Este método se emplea principalmente para la simulación de una normal multivariante, aunque también es válido para muchas otras distribuciones como la \(t\)-multivariante.

En el caso de normalidad, el resultado general es el siguiente.

Proposición 6.1
Si \(\mathbf{X} \sim \mathcal{N}_d\left( \boldsymbol\mu,\Sigma \right)\) y \(A\) es una matriz \(p\times d\), de rango máximo, con \(p\leq d\), entonces: \[A\mathbf{X} \sim \mathcal{N}_{p}\left(A\boldsymbol\mu,A\Sigma A^t\right).\]

Partiendo de \(\mathbf{Z} \sim \mathcal{N}_d\left( \mathbf{0},I_d\right)\), se podrían considerar distintas factorizaciones de la matriz de covarianzas:

  • Factorización espectral: \(\Sigma=H\Lambda H^t =H\Lambda^{1/2}(H\Lambda^{1/2})^t\), donde \(H\) es una matriz ortogonal (i.e. \(H^{-1}=H^{t}\)), cuyas columnas son los autovectores de la matriz \(\Sigma\), y \(\Lambda\) es una matriz diagonal, cuya diagonal esta formada por los correspondientes autovalores (positivos). De donde se deduce que:

\[\mathbf{X} =\boldsymbol\mu + H\Lambda^{1/2}\mathbf{Z} \sim \mathcal{N}_d\left( \boldsymbol\mu,\Sigma \right).\]

  • Factorización de Cholesky: \(\Sigma=LL^t\), donde \(L\) es una matriz triangular inferior (fácilmente invertible), por lo que: \[\mathbf{X} =\boldsymbol\mu + L\mathbf{Z} \sim \mathcal{N}_d\left( \boldsymbol\mu,\Sigma \right).\]

Desde el punto de vista de la eficiencia computacional la factorización de Cholesky sería la preferible. Pero en ocasiones, para evitar problemas numéricos (por ejemplo, en el caso de matrices definidas positivas, i.e. con autovalores nulos) puede ser más adecuado emplear la factorización espectral. En el primer caso el algoritmo sería el siguiente:

Algoritmo 6.2 (de simulación de una normal multivariante)

  1. Obtener la factorización de Cholesky \(\Sigma=LL^t\).

  2. Simular \(\mathbf{Z} =\left( Z_1,Z_2,\ldots,Z_d\right)\) i.i.d. \(\mathcal{N}\left( 0,1\right)\).

  3. Hacer \(\mathbf{X} = \boldsymbol\mu + L\mathbf{Z}\).

  4. Repetir los pasos 2 y 3 las veces necesarias.


Nota: Hay que tener en cuenta el resultado del algoritmo empleado para la factorización de Cholesky. Por ejemplo si se obtiene \(\Sigma=U^tU\), hará que emplear \(L=U^t.\)

Ejemplo 6.4 (simulación de datos funcionales o temporales)

Supongamos que el objetivo es generar una muestra de tamaño nsim de la variable funcional: \[X(t)=\sin\left( 2\pi t\right) +\varepsilon\left( t\right)\] con \(0\leq t \leq1\) y \(Cov(\varepsilon\left( t_1 \right) , \varepsilon\left( t_2 \right) ) = e^{-\left\Vert t_1-t_2 \right\Vert }\), considerando 100 puntos de discretización (se puede pensar también que es un proceso temporal).

nsim <- 20
n <- 100
t <- seq(0, 1, length = n)
# Media
mu <- sin(2*pi*t)
# Covarianzas
t.dist <- as.matrix(dist(t))
x.cov <- exp(-t.dist)

Para la factorización de la matriz de covarianzas emplearemos la función chol del paquete base de R (si las dimensiones fueran muy grandes podría ser preferible emplear otros paquetes, e.g. spam::chol.spam), pero al devolver la matriz triangular superior habrá que transponer el resultado:

U <- chol(x.cov)
L <- t(U)

Si queremos simular una realización:

set.seed(1)
head(mu + L %*% rnorm(n))
##         [,1]
## 1 -0.6264538
## 2 -0.5307633
## 3 -0.5797968
## 4 -0.2844357
## 5 -0.1711797
## 6 -0.2220796

y para simular nsim:

z <- matrix(rnorm(nsim * n), nrow = n)
x <- mu + L %*% z

matplot(t, x, type = "l", ylim = c(-3.5, 3.5))
lines(t, mu, lwd = 2)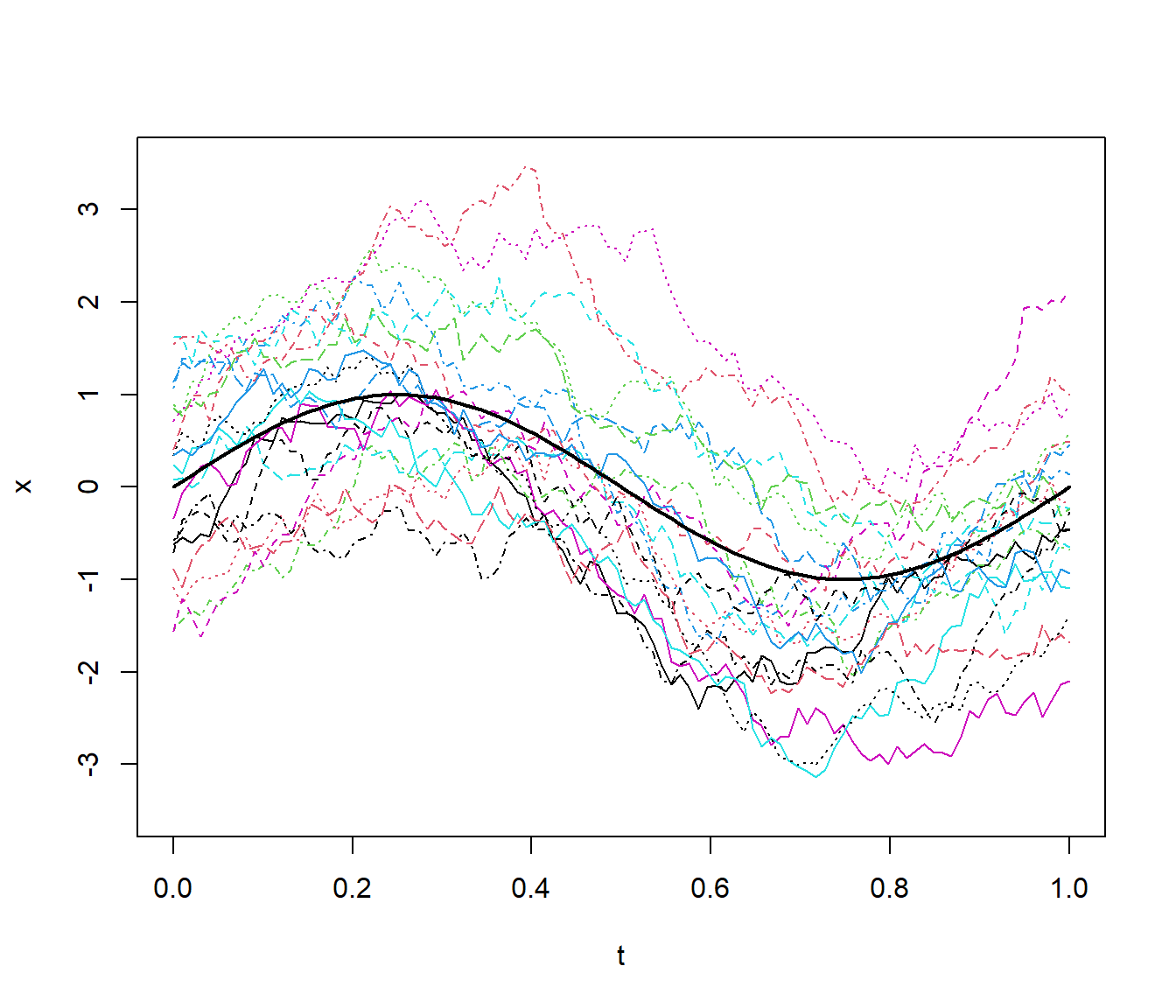
Realizaciones del proceso funcional del Ejemplo 6.4, obtenidas a partir de la factorización de Cholesky.

Figura 6.2: Realizaciones del proceso funcional del Ejemplo 6.4, obtenidas a partir de la factorización de Cholesky.

Alternativamente se podría emplear, por ejemplo, la funcion mvrnorm del paquete MASS que emplea la factorización espectral (eigen) (y que tiene en cuenta una tolerancia relativa para correguir autovalores negativos próximos a cero):

library(MASS)
mvrnorm
## function (n = 1, mu, Sigma, tol = 1e-06, empirical = FALSE, EISPACK = FALSE) 
## {
##     p <- length(mu)
##     if (!all(dim(Sigma) == c(p, p))) 
##         stop("incompatible arguments")
##     if (EISPACK) 
##         stop("'EISPACK' is no longer supported by R", domain = NA)
##     eS <- eigen(Sigma, symmetric = TRUE)
##     ev <- eS$values
##     if (!all(ev >= -tol * abs(ev[1L]))) 
##         stop("'Sigma' is not positive definite")
##     X <- matrix(rnorm(p * n), n)
##     if (empirical) {
##         X <- scale(X, TRUE, FALSE)
##         X <- X %*% svd(X, nu = 0)$v
##         X <- scale(X, FALSE, TRUE)
##     }
##     X <- drop(mu) + eS$vectors %*% diag(sqrt(pmax(ev, 0)), p) %*% 
##         t(X)
##     nm <- names(mu)
##     if (is.null(nm) && !is.null(dn <- dimnames(Sigma))) 
##         nm <- dn[[1L]]
##     dimnames(X) <- list(nm, NULL)
##     if (n == 1) 
##         drop(X)
##     else t(X)
## }
## <bytecode: 0x000000003d174888>
## <environment: namespace:MASS>
x <- mvrnorm(nsim, mu, x.cov)

matplot(t, t(x), type = "l")
lines(t, mu, lwd = 2)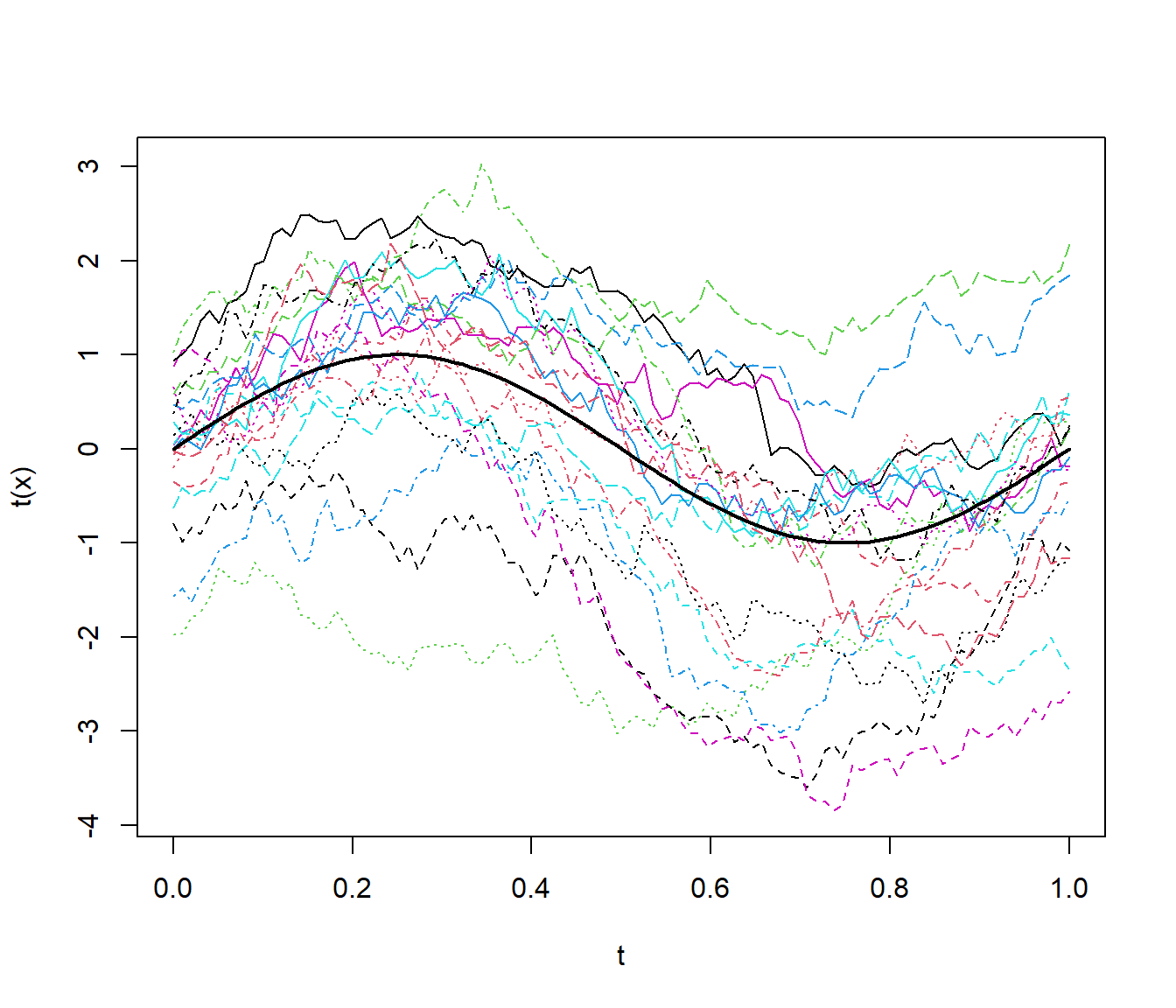
Realizaciones del proceso funcional del Ejemplo 6.4, obtenidas empleando la función MASS::mvrnorm.

Figura 6.3: Realizaciones del proceso funcional del Ejemplo 6.4, obtenidas empleando la función MASS::mvrnorm.

Otros métodos para variables continuas relacionados con la factorización de la matriz de covarianzas son el método FFT (transformada rápida de Fourier; e.g. Davies y Harte, 1987) o el Circular embedding (Dietrich and Newsam, 1997), que realmente son el mismo.