3.3 El problema de la dependencia

En el caso de dependencia, bajo condiciones muy generales se verifica la ley débil de los grandes números. Sin embargo, la estimación de la precisión se complica: \[Var\left( \overline{X}\right) =\frac{1}{n^{2}}\left( \sum_{i=1}^{n}Var\left( X_{i} \right) + 2\sum_{i<j}Cov\left( X_{i},X_{j}\right) \right).\]

Ejemplo 3.3 (aproximación de una proporción bajo dependencia cadena de Markov)

Supongamos que en A Coruña llueve de media uno de cada tres días al año, y que la probabilidad de que un día llueva solo depende de lo que ocurrió el día anterior, siendo 0.94 si el día anterior llovió y 0.03 si no.

Podemos generar valores de la variable indicadora de día lluvioso con el siguiente código:

# Variable dicotómica 0/1 (FALSE/TRUE)  
set.seed(1)
nsim <- 10000
alpha <- 0.03 # prob de cambio si seco
beta <- 0.06  # prob de cambio si lluvia
rx <- logical(nsim) # x == "llueve"
rx[1] <- FALSE # El primer día no llueve
for (i in 2:nsim)
  rx[i] <- if (rx[i-1]) runif(1) > beta else runif(1) < alpha

Si generamos el gráfico de convergencia asumiendo independencia:

n <- 1:nsim
est <- cumsum(rx)/n
esterr <- sqrt(est*(1-est)/(n-1)) # OJO! Supone independencia
plot(est, type="l", lwd=2, ylab="Probabilidad", 
     xlab="Número de simulaciones", ylim=c(0,0.6))
abline(h = est[nsim], lty=2)
lines(est + 2*esterr, lty=2) 
lines(est - 2*esterr, lty=2)
abline(h = 1/3, col="darkgray") # Probabilidad teórica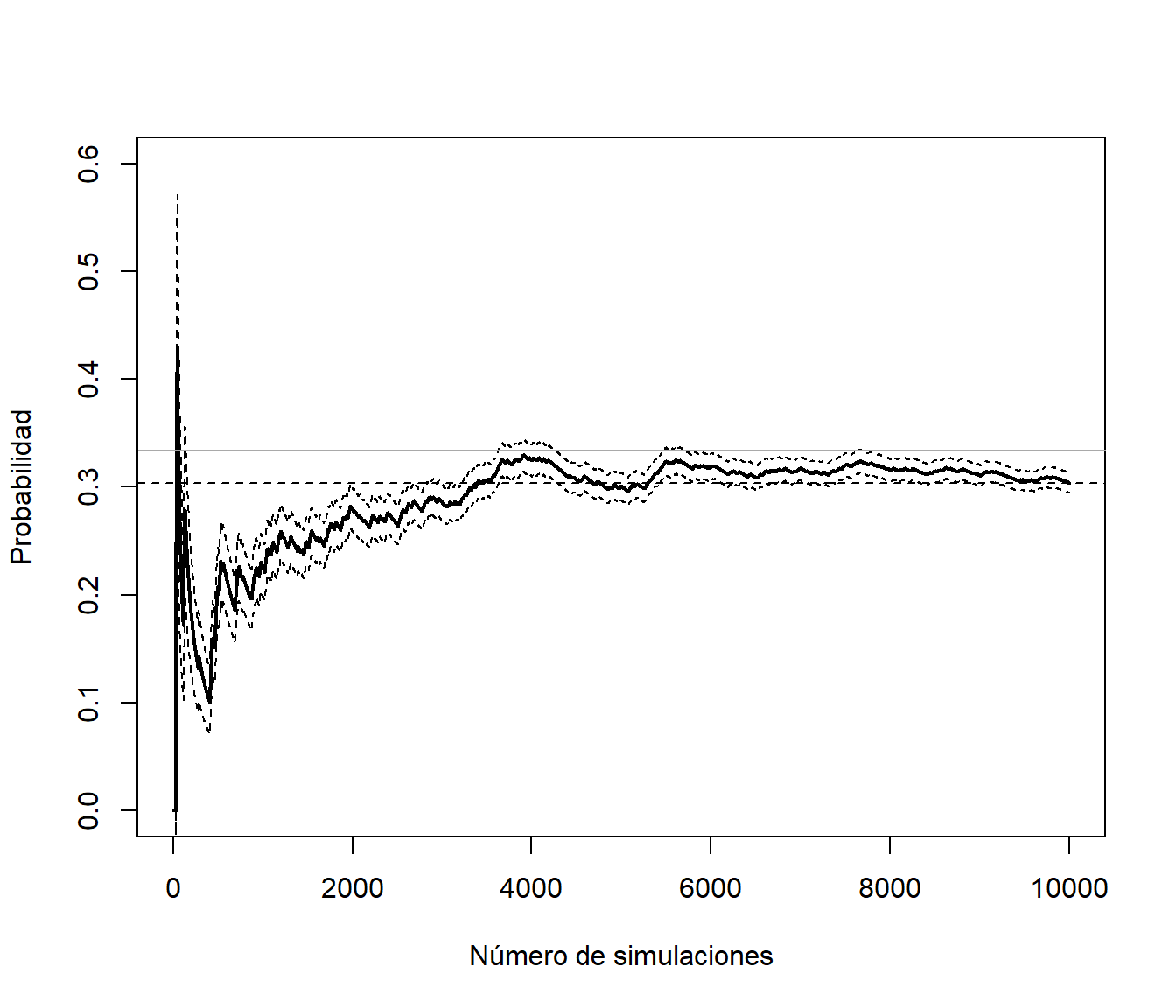

Figura 3.5: Gráfico de convergencia incluyendo el error de la aproximación (calculado asumiendo independencia).

La probabilidad teórica, obtenida empleando resultados de cadenas de Markov, es \(p = 1/3\) y la aproximación de la proporción sería correcta (es consistente):

est[nsim]

## [1] 0.3038

Sin embargo, al ser datos dependientes, la aproximación anterior del error estándar no es adecuada:

esterr[nsim]

## [1] 0.004599203

En este caso al haber dependencia positiva se produce una subestimación del verdadero error estándar. Podemos generar el gráfico de autocorrelaciones:

acf(as.numeric(rx))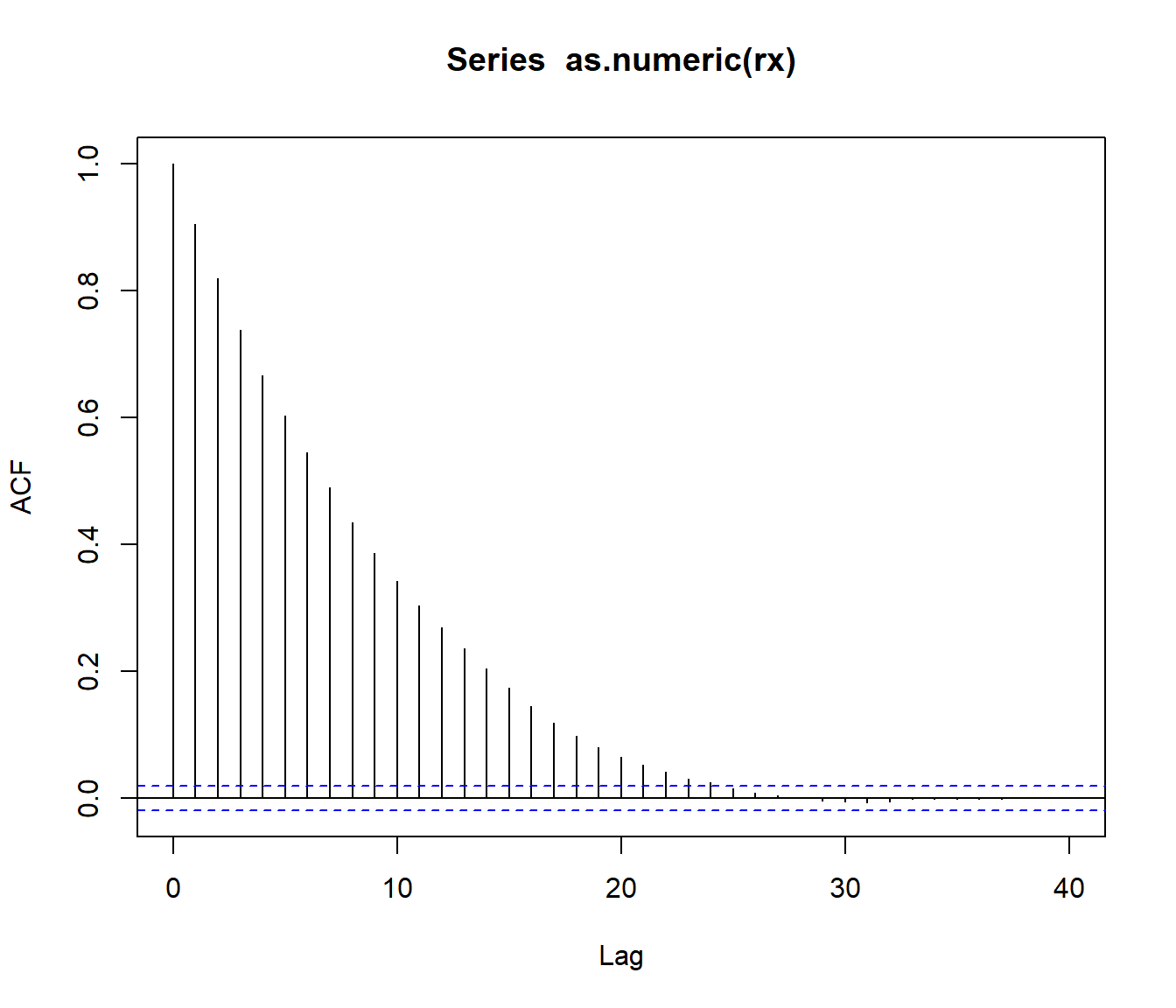

Figura 3.6: Correlograma de la secuencia indicadora de días de lluvia.

El gráfico anterior sugiere que si solo tomamos 1 de cada 25 valores podría ser razonable asumir independencia.

lag <- 24
xlag <- c(rep(FALSE, lag), TRUE)
rxi <- rx[xlag]
acf(as.numeric(rxi))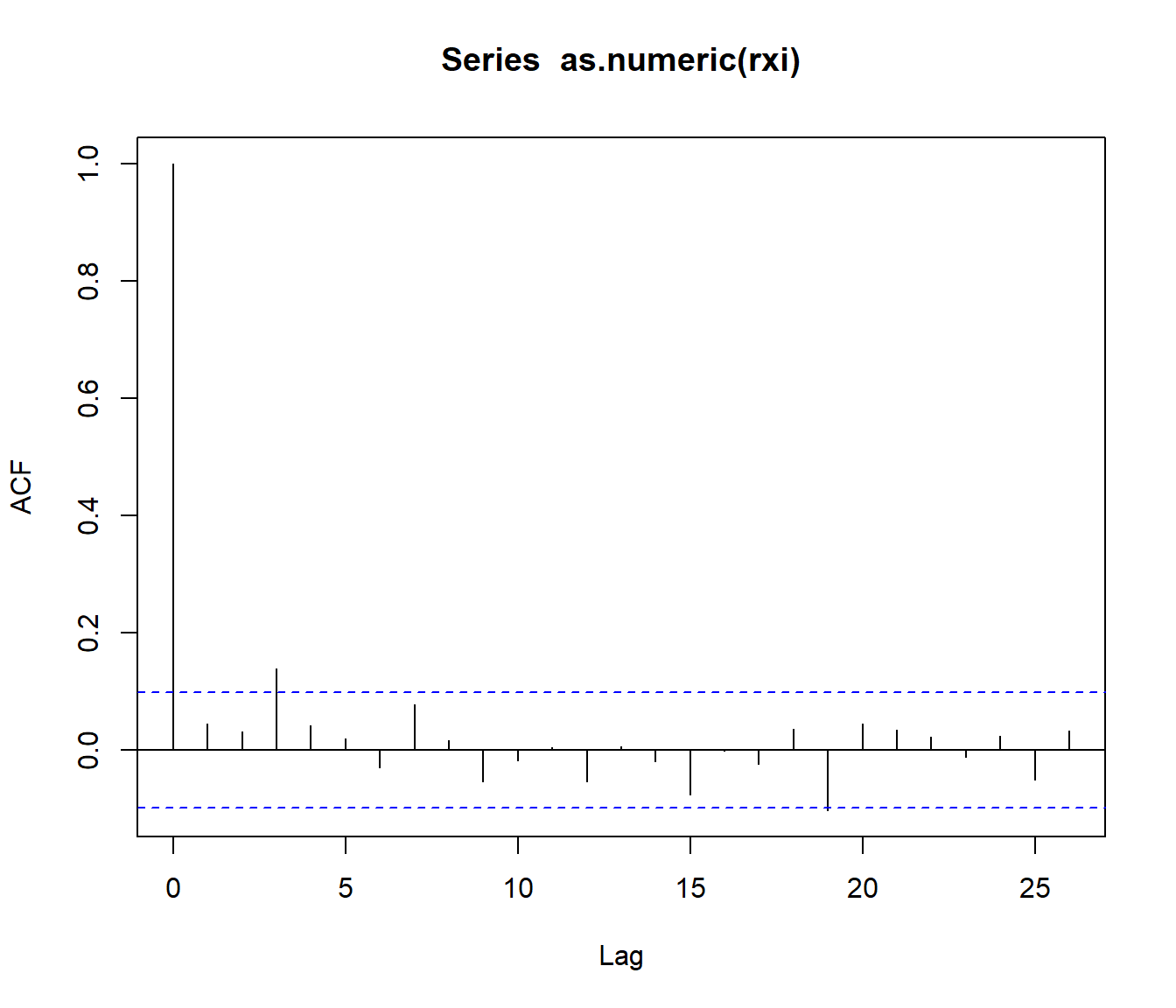

Figura 3.7: Correlograma de la subsecuencia de días de lluvia obtenida seleccionando uno de cada 25 valores.

nrxi <- length(rxi)
n <- 1:nrxi
est <- cumsum(rxi)/n
esterr <- sqrt(est*(1-est)/(n-1))
plot(est, type="l", lwd=2, ylab="Probabilidad", 
     xlab=paste("Número de simulaciones /", lag + 1), ylim=c(0,0.6))
abline(h = est[length(rxi)], lty=2)
lines(est + 2*esterr, lty=2) # Supone independencia
lines(est - 2*esterr, lty=2)
abline(h = 1/3, col="darkgray")     # Prob. teor. cadenas Markov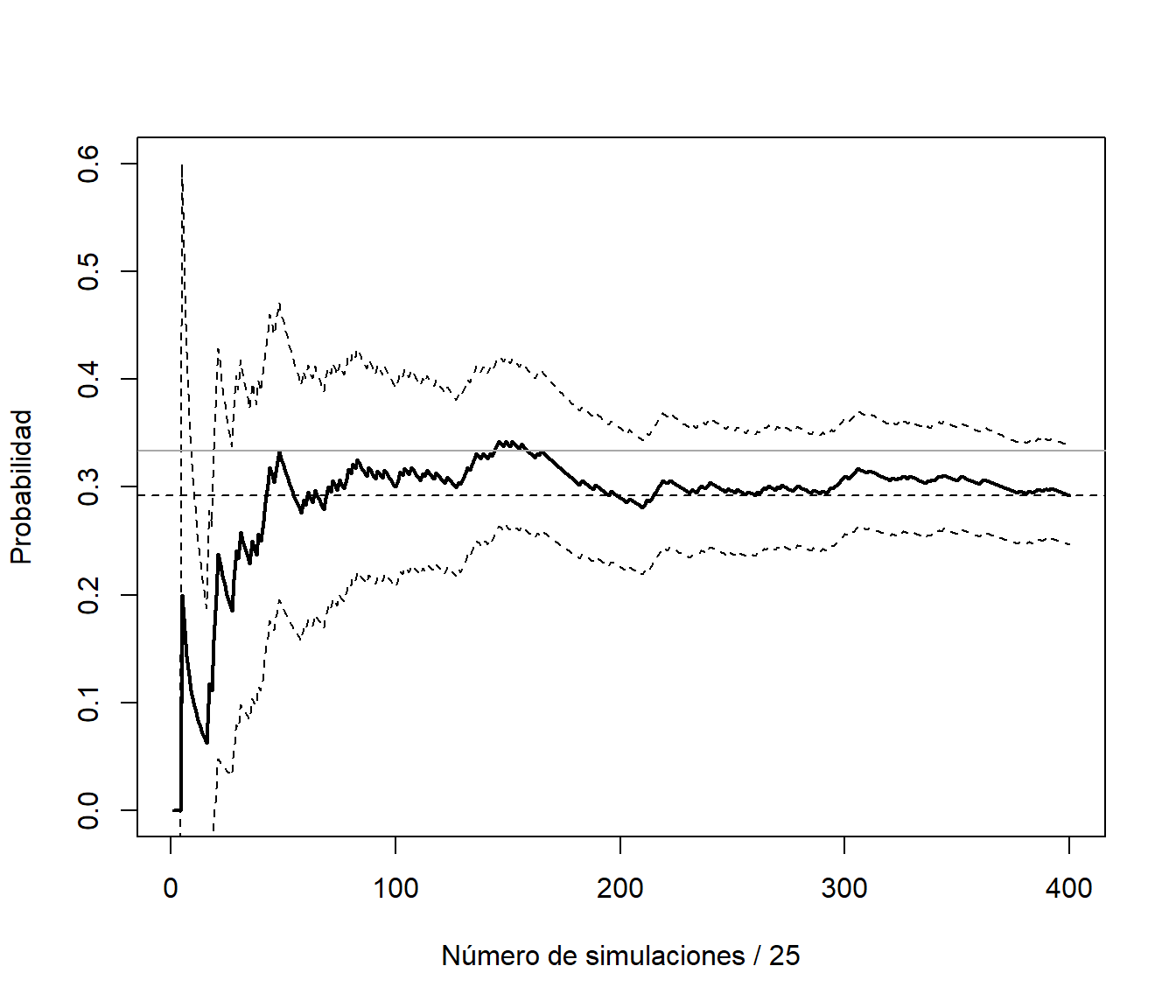

Figura 3.8: Gráfico de convergencia de la aproximación de la probabilidad a partir de la subsecuencia de días de lluvia (calculando el error de aproximación asumiendo independencia).

Esta forma de proceder podría ser adecuada para tratar de aproximar la precisión:

esterr[nrxi]

## [1] 0.02277402

pero no sería la más eficiente para aproximar la media. Siempre es preferible emplear todas las observaciones.

Por ejemplo, se podría pensar en considerar las medias de grupos de 25 valores consecutivos y suponer que hay independencia entre ellas:

rxm <- rowMeans(matrix(rx, ncol = lag + 1, byrow = TRUE))
nrxm <- length(rxm)
n <- 1:nrxm
est <- cumsum(rxm)/n
esterr <- sqrt((cumsum(rxm^2)/n - est^2)/(n-1)) # Errores estándar
plot(est, type="l", lwd=2, ylab="Probabilidad", 
     xlab=paste("Número de simulaciones /", lag + 1), ylim=c(0,0.6))
abline(h = est[length(rxm)], lty=2)
lines(est + 2*esterr, lty=2) # OJO! Supone independencia
lines(est - 2*esterr, lty=2)
abline(h = 1/3, col="darkgray")     # Prob. teor. cadenas Markov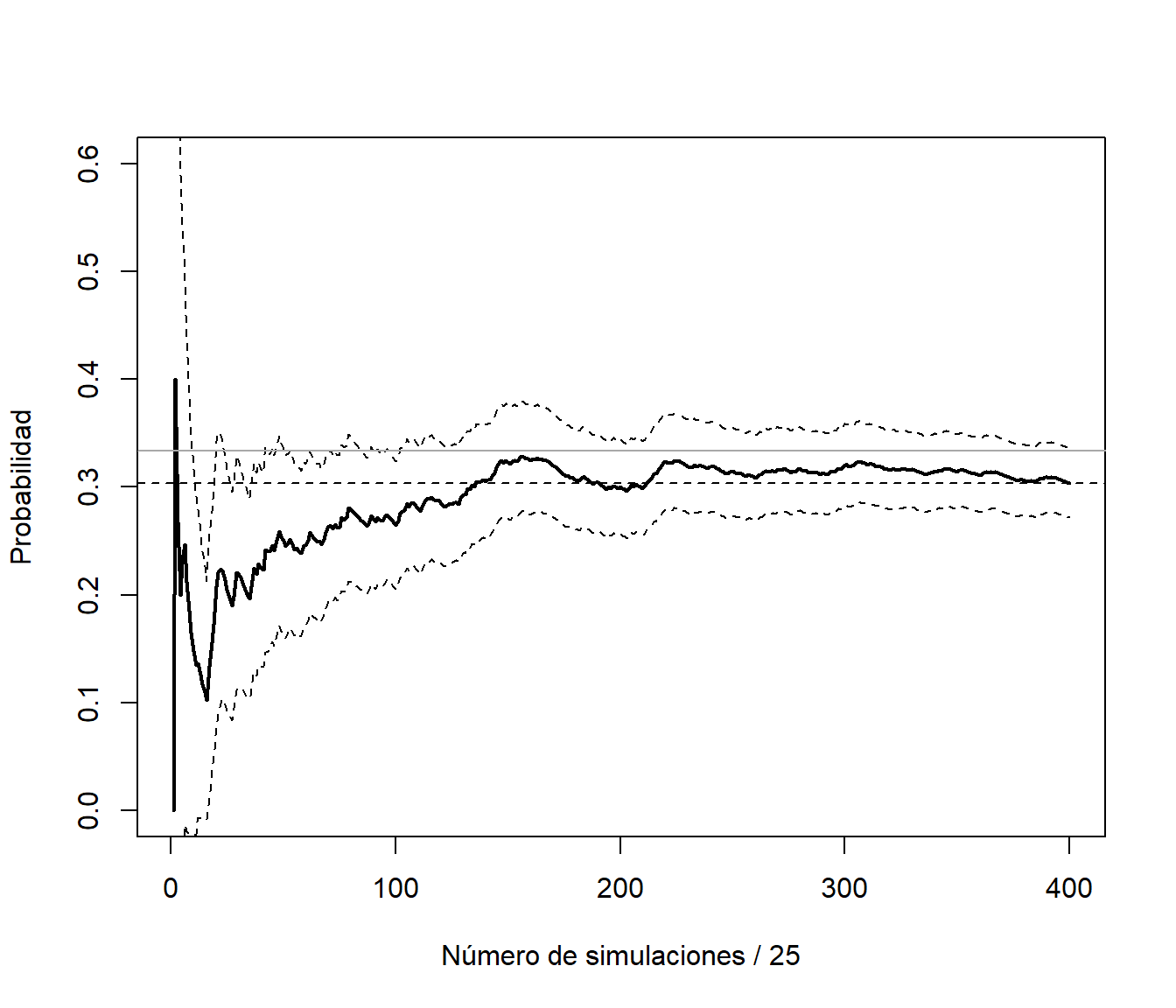

Figura 3.9: Gráfico de convergencia de las medias por lotes.

Esta es la idea del método de medias por lotes (batch means; macro-micro replicaciones) para la estimación de la precisión. Supongamos que la correlación entre \(X_i\) y \(X_{i+k}\) es aproximadamente nula, y consideramos las subsecuencias (lotes) \((X_{t+1},X_{t+2},\ldots,X_{t+k})\) con \(t=(j-1)k\), \(j=1,\ldots,m\) y \(n = mk\). Entonces:

\[\begin{aligned} Var \left(\bar X \right) &= Var \left(\frac{1}{n} \sum_{i=1}^n X_i\right) = Var \left( \frac{1}{m}\sum_{j=1}^m \left(\frac{1}{k} \sum_{t=(i-1)k + 1}^{ik} X_t\right) \right) \\ &\approx \frac{1}{m^2} \sum_{j=1}^m Var \left(\frac{1}{k} \sum_{t=(i-1)k + 1}^{ik} X_t\right) = \frac{1}{m} Var \left(\bar{X}_k \right) \end{aligned}\] donde \(\bar{X}_k\) es la media de una subsecuencia de longitud \(k\).

Alternativamente se podría recurrir a la generación de múltiples secuencias independientes entre sí:

# Variable dicotómica 0/1 (FALSE/TRUE)  
set.seed(1)
nsim <- 1000
nsec <- 10
alpha <- 0.03 # prob de cambio si seco
beta <- 0.06  # prob de cambio si lluvia
rxm <- matrix(FALSE, nrow = nsec, ncol= nsim)
for (i in 1:nsec) {
  # rxm[i, 1] <- FALSE # El primer día no llueve
  # rxm[i, 1] <- runif(1) < 1/2 # El primer día llueve con probabilidad 1/2
  rxm[i, 1] <- runif(1) < 1/3 # El primer día llueve con probabilidad 1/3 (ideal)
  for (j in 2:nsim)
    rxm[i, j] <- if (rxm[i, j-1]) runif(1) > beta else runif(1) < alpha
}

La idea sería considerar las medias de las series como una muestra independiente de una nueva variable y estimar su varianza de la forma habitual:

# Media de cada secuencia
n <- 1:nsim
est <- apply(rxm, 1, function(x) cumsum(x)/n)
matplot(n, est, type = 'l', lty = 3, col = "lightgray",
     ylab="Probabilidad", xlab="Número de simulaciones")
# Aproximación
mest <- apply(est, 1, mean)
lines(mest, lwd = 2)
abline(h = mest[nsim], lty = 2)
# Precisión
mesterr <- apply(est, 1, sd)/sqrt(nsec)
lines(mest + 2*mesterr, lty = 2)
lines(mest - 2*mesterr, lty = 2)
# Prob. teor. cadenas Markov
abline(h = 1/3, col="darkgray")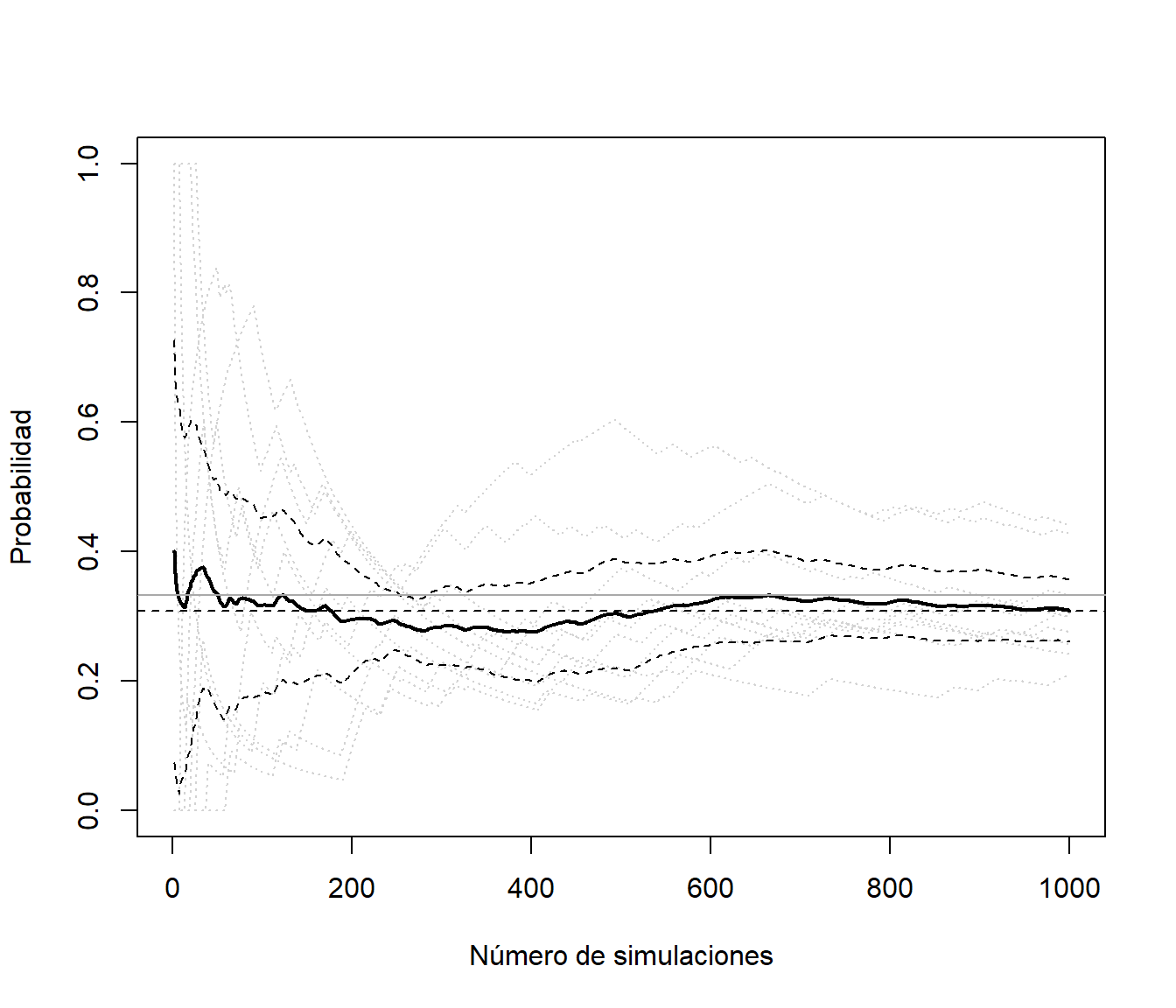     

Figura 3.10: Gráfico de convergencia de la media de 10 secuencias generadas de forma independiente.

# Aproximación final
mest[nsim] # mean(rxm)

## [1] 0.3089

# Error estándar
mesterr[nsim]

## [1] 0.02403491

Trataremos este tipo de problemas en la diagnosis de algoritmos Monte Carlo de Cadenas de Markov (MCMC, Capítulo 10). Aparecen también en la simulación dinámica (por eventos o cuantos).

3.3.1 Periodo de calentamiento

En el caso de simulación de datos dependientes (simulación dinámica) pueden aparecer problemas de estabilización. Puede ocurrir que el sistema evolucione lentamente en el tiempo hasta alcanzar su distribución estacionaria, siendo muy sensible a las condiciones iniciales con las que se comienzó la simulación. En tal caso resulta conveniente ignorar los resultados obtenidos durante un cierto período inicial de tiempo (denominado período de calentamiento o estabilización), cuyo único objeto es conseguir que se estabilice la distribución de probabilidad.

Como ejemplo comparamos la simulación del Ejemplo 3.3 con la obtenida considerando como punto de partida un día lluvioso (con una semilla distinta para evitar dependencia).

set.seed(2)
nsim <- 10000
rx2 <- logical(nsim)
rx2[1] <- TRUE # El primer día llueve
for (i in 2:nsim)
  rx2[i] <- if (rx2[i-1]) runif(1) > beta else runif(1) < alpha
n <- 1:nsim
est <- cumsum(rx)/n
est2 <- cumsum(rx2)/n
plot(est, type="l", ylab="Probabilidad", 
     xlab="Número de simulaciones", ylim=c(0,0.6))
lines(est2, lty = 2)
# Ejemplo periodo calentamiento nburn = 2000
abline(v = 2000, lty = 3)
# Prob. teor. cadenas Markov
abline(h = 1/3, col="darkgray")     

En estos casos puede ser recomendable ignorar los primeros valores generados (por ejemplo los primeros 2000) y recalcular los estadísticos deseados.

También trataremos este tipo de problemas en la diagnosis de algoritmos MCMC.

Ejemplo 3.4 (simulación de un proceso autorregresivo serie de tiempo)

\[X_t = \mu + \rho * (X_{t-1} - \mu) + \varepsilon_t\] Podemos tener en cuenta que en este caso la varianza es: \[\textrm{var}(X_t)=\operatorname{E}(X_t^2)-\mu^2=\frac{\sigma_\varepsilon^2}{1-\rho^2}.\]

Establecemos los parámetros:

nsim <- 200   # Numero de simulaciones
xmed <- 0     # Media
rho <- 0.5    # Coeficiente AR
nburn <- 10   # Periodo de calentamiento (burn-in)

Se podría fijar la varianza del error:

evar <- 1
# Varianza de la respuesta
xvar <- evar / (1 - rho^2)

pero la recomendación sería fijar la varianza de la respuesta:

xvar <- 1     
# Varianza del error
evar <- xvar*(1 - rho^2)

Para simular la serie, al ser un \(AR(1)\), normalmente simularíamos el primer valor

x[1] <- rnorm(1, mean = xmed, sd = sqrt(xvar))

o lo fijamos a la media. Después generamos los siguientes valores de forma recursiva.

Como ejemplo nos alejamos un poco de la distribución estacionaria, para que el “periodo de calentamiento” sea mayor:

set.seed(1)
x <- numeric(nsim + nburn)
# Establecer el primer valor 
x[1] <- -10
# Simular el resto de la secuencia
for (i in 2:length(x))
  x[i] <- xmed + rho*(x[i-1] - xmed) + rnorm(1, sd=sqrt(evar))
x <- as.ts(x)
plot(x)
abline(v = nburn, lty = 2)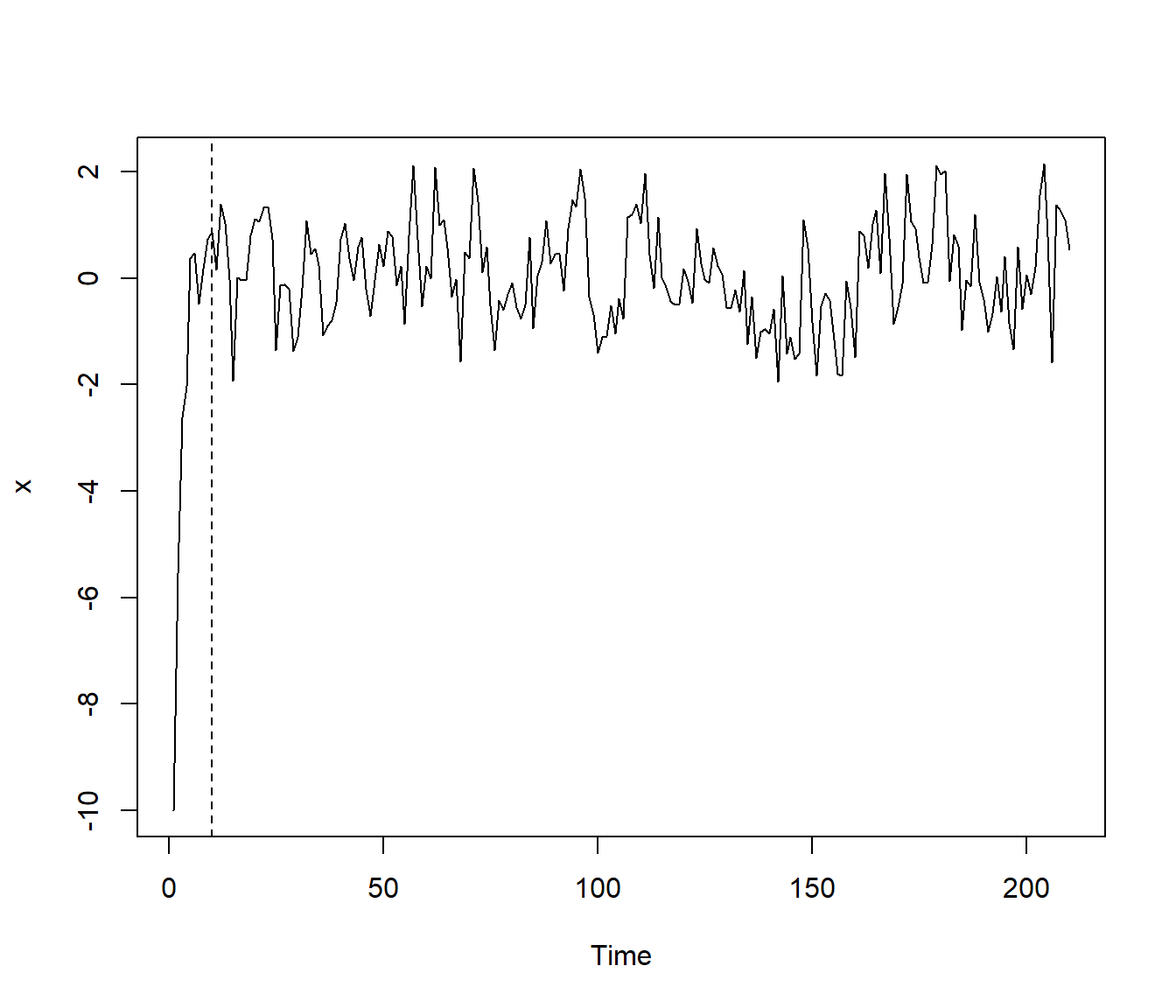

Figura 3.11: Ejemplo de una simulación de una serie de tiempo autorregresiva.

y eliminamos el periodo de calentamiento:

rx <- x[-seq_len(nburn)]

Para simular una serie de tiempo en R se puede emplear la función arima.sim del paquete base stats. En este caso el periodo de calentamiento se establece mediante el parámetro n.start (que se fija automáticamente a un valor adecuado).

Por ejemplo, podemos generar este serie autoregresiva con:

rx2 <- arima.sim(list(order = c(1,0,0), ar = rho), n = nsim, 
                 n.start = nburn, sd = sqrt(evar))

La recomendación es fijar la varianza de las series simuladas si se quieren comparar resultados considerando distintos parámetros de dependencia.