6.7 Simulación de distribuciones multivariantes discretas
En el caso de una distribución \(d\)-dimensional discreta el procedimiento habitual es simular una variable aleatoria discreta unidimensional equivalente. Este tipo de procedimientos son conocidos como métodos de etiquetado o codificación y la idea básica consistiría en construir un indice unidimensional equivalente al indice multidimensional, mediante una función de etiquetado \(l(\mathbf{i}) = l\left(i_1, i_2, \ldots,i_d \right) \in \mathbb{N}\).
Si la variable discreta multidimensional tiene soporte finito, este tipo de recodificación se puede hacer de forma automática en R cambiando simplemente el indexado21 (empleando la función as.vector() para cambiar a un indexado unidimensional y posteriormente las funciones as.matrix(), o as.array(), para reconstruir el indexado multidimensional).
Como ejemplo ilustrativo, en el caso bidimensional, podríamos emplear el siguiente código:
xy <- outer(10*1:4, 1:2, "+")
xy## [,1] [,2]
## [1,] 11 12
## [2,] 21 22
## [3,] 31 32
## [4,] 41 42z <- as.vector(xy)
z## [1] 11 21 31 41 12 22 32 42xy <- matrix(z, ncol = 2)
xy## [,1] [,2]
## [1,] 11 12
## [2,] 21 22
## [3,] 31 32
## [4,] 41 42Suponiendo que la primera componente toma \(I\) valores distintos, la función de etiquetado para calcular el índice unidimensional a partir de uno bidimensional sería: \[l(i, j) = I(j-1) + i\]
nx <- nrow(xy)
l <- function(i, j) nx*(j-1) + i
z[l(2, 1)]## [1] 21z[l(3, 2)]## [1] 32Para recuperar el índice bidimensional se emplearía la inversa de la función de etiquetado: \[l^{-1}( k ) =\left( (k -1) \operatorname{mod} I + 1, \left\lfloor \frac{k - 1}{I}\right\rfloor + 1\right)\]
linv <- function(k) cbind((k - 1) %% nx + 1, floor((k - 1)/nx) + 1)
# Para el caso multidimensional (1d => md): imd <- arrayInd(i1d, dim(xy))
xy[linv(2)]## [1] 21xy[linv(7)]## [1] 32Realmente lo que ocurre internamente en R es que un objeto matrix o array está almacenado como un vector y admite un indexado multidimensional si está presente un atributo dim:
dim(z) <- c(4, 2)
z## [,1] [,2]
## [1,] 11 12
## [2,] 21 22
## [3,] 31 32
## [4,] 41 42dim(z) <- c(2, 2, 2)
z## , , 1
##
## [,1] [,2]
## [1,] 11 31
## [2,] 21 41
##
## , , 2
##
## [,1] [,2]
## [1,] 12 32
## [2,] 22 42dim(z) <- NULL
z## [1] 11 21 31 41 12 22 32 42Si la variable discreta multidimensional no tiene soporte finito, se podrían emplear métodos de codificación más avanzados (ver Cao, 2002, Sección 6.3), aunque no se podría guardar la función de masa de probabilidad en una tabla.
No obstante, se podría emplear el indexado anterior si todas las componentes menos una (la correspondiente al índice j en el ejemplo anterior) toman un número finito de valores.
6.7.1 Simulación de una variable discreta bidimensional
Consideramos datos recogidos en un estudio de mejora de calidad en una fábrica de semiconductores. Se obtuvo una muestra de obleas que se clasificaron dependiendo de si se encontraron partículas en la matriz que producía la oblea y de si la calidad de oblea era buena (para más detalles ver Hall, 1994).
n <- c(320, 14, 80, 36)
particulas <- gl(2, 1, 4, labels = c("no", "si"))
calidad <- gl(2, 2, labels = c("buena", "mala"))
df <- data.frame(n, particulas, calidad)
df## n particulas calidad
## 1 320 no buena
## 2 14 si buena
## 3 80 no mala
## 4 36 si malaEn lugar de estar en el formato de un conjunto de datos (data.frame) puede que los datos estén en formato de tabla (table, matrix):
tabla <- xtabs(n ~ calidad + particulas)
tabla## particulas
## calidad no si
## buena 320 14
## mala 80 36Lo podemos convertir directamente a data.frame:
as.data.frame(tabla)## calidad particulas Freq
## 1 buena no 320
## 2 mala no 80
## 3 buena si 14
## 4 mala si 36En este caso estimamos22 las probabilidades a partir de las frecuencias:
df$p <- df$n/sum(df$n)
df## n particulas calidad p
## 1 320 no buena 0.71111111
## 2 14 si buena 0.03111111
## 3 80 no mala 0.17777778
## 4 36 si mala 0.08000000En formato tabla:
pij <- tabla/sum(tabla)
pij## particulas
## calidad no si
## buena 0.71111111 0.03111111
## mala 0.17777778 0.08000000Para simular la variable bidimensional consideramos una variable unidimensional de índices:
z <- 1:nrow(df)
z## [1] 1 2 3 4Con probabilidades:
pz <- df$p
pz## [1] 0.71111111 0.03111111 0.17777778 0.08000000Si las probabilidades estuviesen en una matriz, las convertiríamos a un vector con:
as.vector(pij)## [1] 0.71111111 0.17777778 0.03111111 0.08000000Si simulamos la variable unidimensional:
set.seed(1)
nsim <- 20
rz <- sample(z, nsim, replace = TRUE, prob = pz)Podríamos obtener simulaciones bidimensionales, por ejemplo:
etiquetas <- as.matrix(df[c('particulas', 'calidad')])
rxy <- etiquetas[rz, ]
head(rxy)## particulas calidad
## [1,] "no" "buena"
## [2,] "no" "buena"
## [3,] "no" "buena"
## [4,] "si" "mala"
## [5,] "no" "buena"
## [6,] "si" "mala"Alternativamente, si queremos trabajar con data.frames:
etiquetas <- df[c('particulas', 'calidad')]
rxy <- etiquetas[rz, ]
head(rxy)## particulas calidad
## 1 no buena
## 1.1 no buena
## 1.2 no buena
## 4 si mala
## 1.3 no buena
## 4.1 si mala# Si se quieren eliminar las etiquetas de las filas:
row.names(rxy) <- NULL
head(rxy)## particulas calidad
## 1 no buena
## 2 no buena
## 3 no buena
## 4 si mala
## 5 no buena
## 6 si mala6.7.2 Simulación de tablas de contingencia
Podríamos emplear el código anterior para simular tablas de contingencia. En estos casos se suele mantener fijo el tamaño de la muestra, igual al total de la tabla23:
nsim <- sum(n)
set.seed(1)
rz <- sample(z, nsim, replace = TRUE, prob = pz)
rtable <- table(rz) # Tabla de frecuencias unidimensional
matrix(rtable, ncol = 2, dimnames = dimnames(tabla)) # Tabla de frecuencias bidimensional## particulas
## calidad no si
## buena 321 78
## mala 15 36Aunque puede ser preferible emplear directamente rmultinom() si se van a generar muchas:
ntsim <- 1000
rtablas <- rmultinom(ntsim, sum(n), pz)
rtablas[ , 1:5] # Las cinco primeras simulaciones## [,1] [,2] [,3] [,4] [,5]
## [1,] 298 329 323 323 307
## [2,] 15 21 5 15 15
## [3,] 92 68 91 77 92
## [4,] 45 32 31 35 36Ejemplo 6.10 (Distribución del estadístico chi-cuadrado de independencia)
En el contraste chi-cuadrado (tradicional) de independencia (ver Sección A.1.4) se emplea una aproximación continua de la distribución del estadístico bajo la hipótesis nula (la distribución asintótica \(\chi^2\), con una corrección por continuidad en tablas dos por dos):
res <- chisq.test(tabla)
res##
## Pearson's Chi-squared test with Yates' continuity correction
##
## data: tabla
## X-squared = 60.124, df = 1, p-value = 8.907e-15Sin embargo la distribución exacta del estadístico del contraste es discreta y como alternativa la podríamos aproximar mediante simulación.
Para simular bajo independencia podemos estimar las probabilidades a partir de las frecuencias marginales de la tabla de contingencia:
pind <- (rowSums(tabla) %o% colSums(tabla))/(sum(tabla)^2)
matrix(pind, nrow = nrow(tabla), dimnames = dimnames(tabla))## particulas
## calidad no si
## buena 0.6597531 0.08246914
## mala 0.2291358 0.02864198Empleando el código anterior podemos generar las simulaciones de las tablas de contingencia (bajo independencia):
ntsim <- 2000
rtablas <- rmultinom(ntsim, sum(n), pind)
rtablas[ , 1:5] # Las cinco primeras simulaciones## [,1] [,2] [,3] [,4] [,5]
## [1,] 292 285 309 303 290
## [2,] 96 105 97 84 113
## [3,] 48 48 36 49 39
## [4,] 14 12 8 14 8A partir de las cuales podemos aproximar por simulación la distribución exacta del estadístico del contraste chi-cuadrado de independencia:
sim.stat <- apply(rtablas, 2, function(x) chisq.test(matrix(x, nrow = nrow(tabla)))$statistic)
hist(sim.stat, freq = FALSE, breaks = 'FD')
# lines(density(sim.stat))
# Distribución asintótica (aproximación chi-cuadrado)
curve(dchisq(x, res$parameter), col = 'blue', add = TRUE) 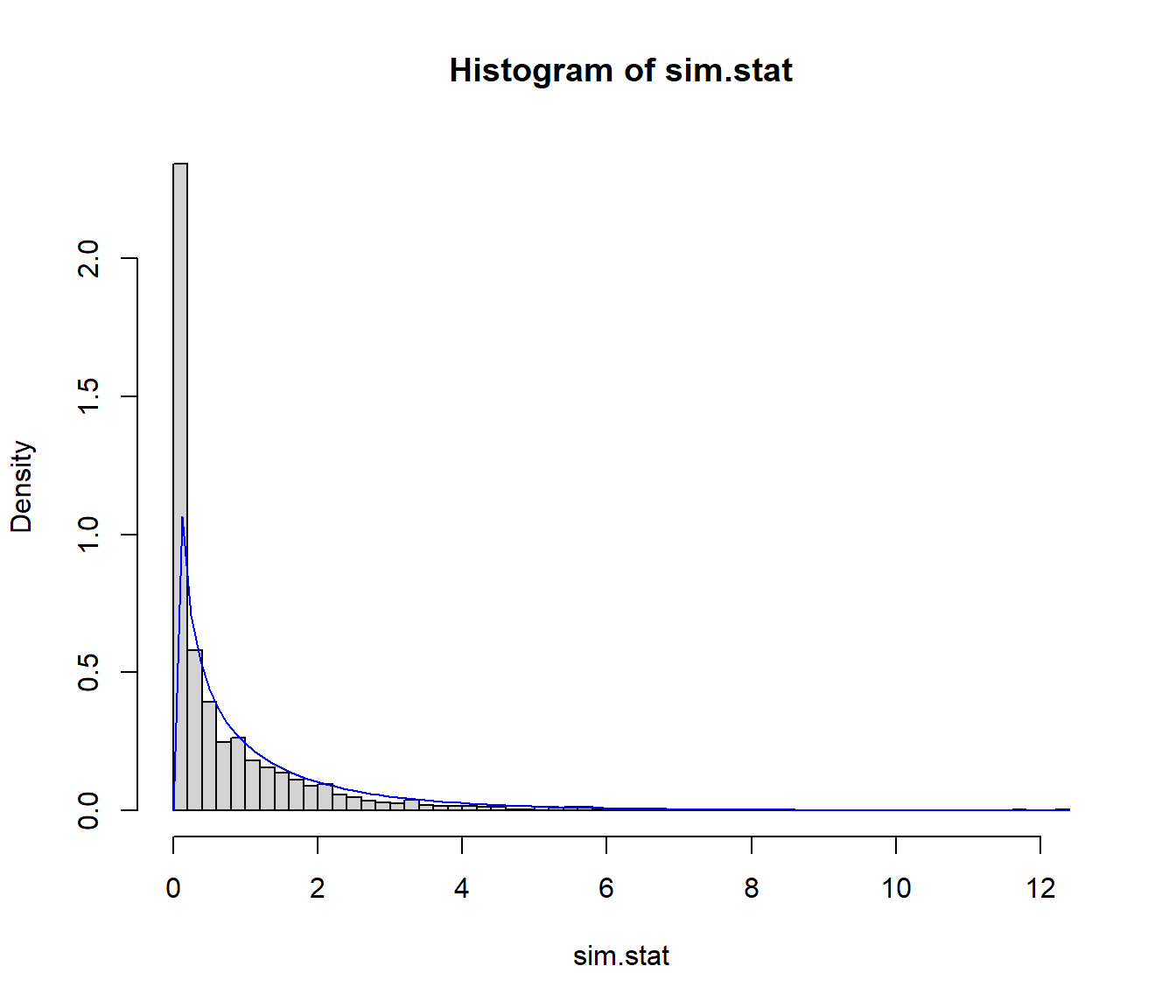
Figura 6.14: Aproximación Monte Carlo de la distribución del estadístico chi-cuadrado bajo independencia.
Como se mostrará en la Sección 7.4.3, podríamos aproximar el \(p\)-valor del contraste de independencia a partir de esta aproximación:
obs.stat <- res$statistic
pvalue.mc <- mean(sim.stat >= obs.stat)
pvalue.mc## [1] 0Esto es similar a lo que realiza la función chisq.test() con la opción simulate.p.value = TRUE (empleando el algoritmo de Patefield, 1981):
chisq.test(tabla, simulate.p.value = TRUE, B = 2000)##
## Pearson's Chi-squared test with simulated p-value (based on 2000
## replicates)
##
## data: tabla
## X-squared = 62.812, df = NA, p-value = 0.0004998En R podemos obtener el índice multidimensional empleando la función
arrayInd(ind, .dim, ...), siendoindun vector de índices unidimensionales.↩︎Como ya se comentó, la simulación empleando un modelo estimado también se denomina bootstrap paramétrico.↩︎
También se podría fijar una de las distribuciones de frecuencias marginales y simular las correspondientes distribuciones condicionadas.↩︎