7.1 Integración Monte Carlo
La integración Monte Carlo se emplea principalmente para aproximar integrales multidimensionales: \[I = \int \cdots \int _D s\left( x_1,\ldots ,x_n\right) dx_1 \cdots dx_n\] donde puede presentar ventajas respecto a los métodos tradicionales de integración numérica (ver Apéndice B), ya que la velocidad de convergencia no depende del número de dimensiones.
La idea es reescibir la expresión de la integral, encontrando una función de densidad \(f\) definida sobre \(D\), de forma que: \[I = \int _D s(\mathbf{x}) d \mathbf{x} = \int h(\mathbf{x})f(\mathbf{x}) d \mathbf{x} = E\left( h(\mathbf{X}) \right)\] donde \(\mathbf{X} \sim f\) (y preferiblemente fácil de simular).
7.1.1 Integración Monte Carlo clásica
En el caso de que el dominio \(D\) sea acotado, la aproximación más simple consiste en considerar una distribución uniforme en \(D\) (i.e. \(f(\mathbf{x})=1_D(\mathbf{x})/|D|\) y \(h(\mathbf{x}) = |D|s(\mathbf{x})\)).
Por simplicidad nos centraremos en el caso unidimensional (el orden de convergencia es independiente del número de dimensiones). Supongamos que nos interesa aproximar: \[I = \int_0^1 s(x) dx\] Si \(x_1,x_2,\ldots ,x_n\) i.i.d. \(\mathcal{U}(0, 1)\) entonces: \[I = E\left( s\left( \mathcal{U}(0, 1) \right) \right) \approx \frac{1}{n}\sum\limits_{i=1}^n s\left( x_i\right)\]
Si el intervalo de integración es genérico: \[I = \int_a^b s(x) dx = (b-a)\int_a^b s(x) \frac1{(b-a)}dx = (b-a)E\left( s\left( \mathcal{U}(a, b) \right) \right).\] Si \(x_1,x_2,\ldots ,x_n\) i.i.d. \(\mathcal{U}(a, b)\): \[I \approx \frac{b-a}{n}\sum\limits_{i=1}^n s\left( x_i\right)\]
Ejemplo 7.1 (integración Monte Carlo clásica)
Como primera aproximación para implementar la integración Monte Carlo clásica para aproximar integrales del tipo: \[I = \int_a^b s(x) dx,\] podríamos considerar la siguiente función:
mc.integral0 <- function(fun, a, b, n) {
# Integración Monte Carlo de `fun()` entre `a` y `b` utilizando una muestra
# (pseudo) aleatoria de tamaño `n`. Se asume que `fun()` es una función de
# una sola variable (no vectorial), `a < b` y `n` entero positivo.
# -----------------------
x <- runif(n, a, b)
fx <- sapply(x, fun) # Si fun fuese vectorial bastaría con: fx <- fun(x)
return(mean(fx) * (b - a))
}Como ejemplo la empleamos para aproximar: \[\int_0^1 4x^4 dx = \frac{4}{5},\]
fun <- function(x) ifelse((x > 0) & (x < 1), 4 * x^4, 0)
# return(4 * x^4)
curve(fun, 0, 1)
abline(h = 0, lty = 2)
abline(v = c(0, 1), lty = 2)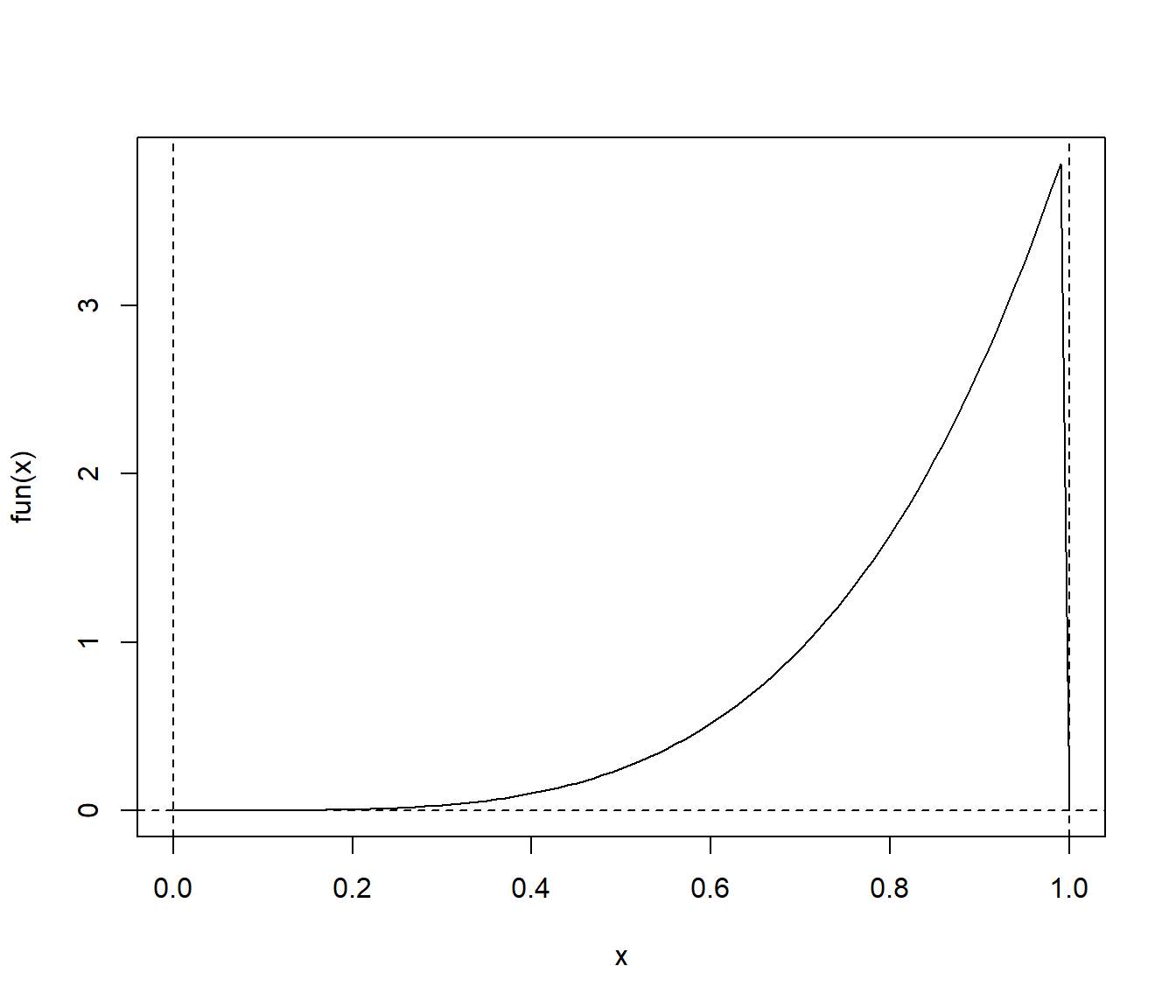
Figura 7.1: Ejemplo de integral en dominio acotado.
set.seed(1)
mc.integral0(fun, 0, 1, 20)## [1] 0.977663mc.integral0(fun, 0, 1, 100)## [1] 0.7311169mc.integral0(fun, 0, 1, 100)## [1] 0.8304299La función mc.integral0 no es adecuada para analizar la convergencia de la aproximación por simulación.
Una alternativa más eficiente para representar gráficamente la convergencia está implementada en la función mc.integral() del paquete simres (fichero mc.plot.R):
library(simres)
mc.integral## function(fun, a, b, n, level = 0.95, plot = TRUE, ...) {
## fx <- sapply(runif(n, a, b), fun) * (b - a)
## result <- if (plot) conv.plot(fx, level = level, ...) else {
## q <- qnorm((1 + level)/2)
## list(approx = mean(fx), max.error = q * sd(fx)/sqrt(n))
## }
## return(result)
## }
## <bytecode: 0x000000003ccd6e08>
## <environment: namespace:simres>set.seed(1)
mc.integral(fun, 0, 1, 5000, ylim = c(0.2, 1.4))## $approx
## [1] 0.8142206
##
## $max.error
## [1] 0.03028194abline(h = 4/5, lty = 2, col = "blue")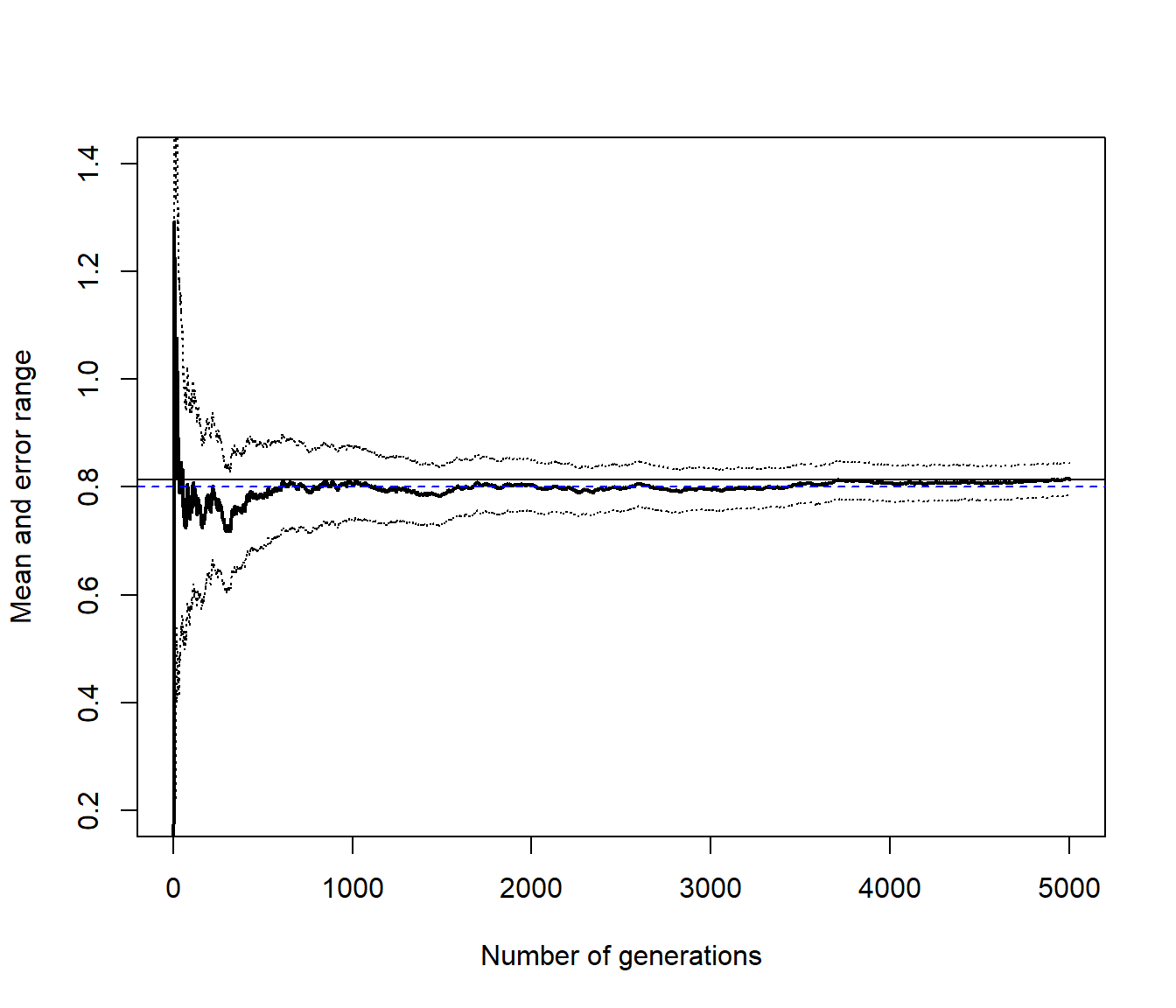
Figura 7.2: Convergencia de la aproximación de la integral mediante simulación.
Si sólo interesa la aproximación:
set.seed(1)
mc.integral(fun, 0, 1, 5000, plot = FALSE)## $approx
## [1] 0.8142206
##
## $max.error
## [1] 0.03028194Nota: Es importante tener en cuenta que la función mc.integral() solo es válida para dominio finito.
7.1.2 Caso general
En lo que resta de esta sección (y en las siguientes) asumiremos que nos interesa aproximar una esperanza: \[\theta = E\left( h\left( X\right) \right) = \int h\left( x\right) f(x)dx\] siendo \(X\sim f\). Entonces, si \(x_1,x_2,\ldots ,x_n\) i.i.d. \(X\): \[\theta \approx \frac{1}{n}\sum\limits_{i=1}^nh\left( x_i\right)\]
Por ejemplo, como en el ejercicio anterior se considera de una función de densidad, se correspondería con el caso general de \(h(x) = x\) y \(f(x) = 4x^3\) para \(0<x<1\). La idea es que, en lugar de considerar una distribución uniforme, es preferible generar más valores donde hay mayor “área” (ver Figura 7.1).
Los pasos serían simular x con densidad \(f\) y aproximar la integral por mean(h(x)).
En este caso podemos generar valores de la densidad objetivo fácilmente mediante el método de inversión, ya que \(F(x) = x^4\) si \(0<x<1\).
rfun <- function(nsim) runif(nsim)^(1/4) # Método de inversión
nsim <- 5000
set.seed(1)
x <- rfun(nsim)
# h <- function(x) x
# res <- mean(h(x)) # Aproximación por simulación
res <- mean(x)
res## [1] 0.7967756# error <- 2*sd(h(x))/sqrt(nsim)
error <- 2*sd(x)/sqrt(nsim)
error## [1] 0.004728174Esta forma de proceder permite aproximar integrales impropias en las que el dominio de integración no es acotado.
Ejemplo 7.2 (integración Monte Carlo con dominio no acotado)
Aproximar: \[\phi(t)=\int_{t}^{\infty}\frac1{\sqrt{2\pi}}e^{-\frac{x^2}2}dx,\] para \(t=4.5\), empleando integración Monte Carlo (aproximación tradicional con dominio infinito).
# h <- function(x) x > 4.5
# f <- function(x) dnorm(x)
set.seed(1)
nsim <- 10^3
x <- rnorm(nsim)
mean(x > 4.5) # mean(h(x))## [1] 0pnorm(-4.5) # valor teórico P(X > 4.5) ## [1] 3.397673e-06De esta forma es difícil que se generen valores (en este caso ninguno) en la región que interesaría para la aproximación de la integral:
any(x > 4.5)## [1] FALSEComo ya se comentó anteriormente, sería preferible generar más valores donde hay mayor “área,” pero en este caso \(f\) concentra la densidad en una región que no resulta de utilidad. Por ese motivo puede ser preferible recurrir a una densidad auxiliar que solvente este problema.