8.2 El Bootstrap uniforme
Suponemos que \(\mathbf{X}=\left( X_1,\ldots ,X_n \right)\) es una una muestra aleatoria simple (m.a.s.) de una población con distribución \(F\) y que estamos interesados en hacer inferencia sobre \(\theta =\theta \left(F \right)\) empleando un estimador \(\hat{\theta} = T\left( \mathbf{X} \right)\). Para ello nos gustaría conocer la distribución en el muestreo de un estadístico \(R\left( \mathbf{X},F \right)\), función del estimador (y por tanto de la muestra) y de la distribución poblacional. Por ejemplo el estimador studentizado: \[R=R\left( \mathbf{X},F \right) = \frac{\hat \theta - \theta}{\sqrt{\widehat{Var}(\hat \theta)}}.\]
A veces podemos calcular directamente la distribución de \(R\left( \mathbf{X},F \right)\), aunque suele depender de cantidades poblacionales, no conocidas en la práctica. Otras veces sólo podemos llegar a aproximar la distribución de \(R\left( \mathbf{X},F \right)\) cuando \(n \rightarrow \infty\). Por ejemplo, bajo normalidad \(X_i \overset{i.i.d.}{\sim} \mathcal{N}\left( \mu ,\sigma^2 \right)\), si el parámetro de interés es la media \[\theta \left( F \right) =\mu =\int x~dF\left( x \right) =\int xf\left( x \right) ~dx\] y consideramos como estimador la media muestral \[\hat{\theta} = T\left( \mathbf{X} \right) = \theta \left( F_n \right) =\int x~dF_n\left( x \right) =\bar{X}.\] Como normalmente en la práctica la varianza es desconocida, podríamos considerar el estadístico: \[R=R\left( \mathbf{X},F \right) =\sqrt{n}\frac{\bar{X}-\mu }{S_{n-1}} \sim t_{n-1},\] donde \(S_{n-1}^2\) es la cuasivarianza muestral: \[S_{n-1}^2=\frac{1}{n-1}\sum_{j=1}^{n}\left( X_j-\bar{X} \right)^2.\] Si \(F\) no es normal entonces la distribución de \(R\) ya no es una \(t_{n-1}\), aunque, bajo condiciones muy generales, \(R\overset{d}{\rightarrow}\mathcal{N}\left(0,1 \right)\).
En el universo bootstrap se reemplaza la distribución poblacional (desconocida) \(F\) por una estimación, \(\hat{F}\), de la misma. A partir de la aproximación \(\hat{F}\) podríamos generar, condicionalmente a la muestra observada, remuestras \[\mathbf{X}^{\ast}=\left( X_1^{\ast},\ldots ,X_n^{\ast} \right)\] con distribución \(X_i^{\ast} \sim \hat{F}\), que demoninaremos remuestras bootstrap. Por lo que podemos hablar de la distribución en el remuestreo de \[R^{\ast}=R\left( \mathbf{X}^{\ast},\hat{F} \right),\] denominada distribución bootstrap.
Una de las consideraciones más importantes al diseñar un buen método de remuestreo bootstrap es imitar por completo el procedimiento de muestreo en la población original (incluyendo el estadístico y las características de su distribución muestral).
Como ya se comentó anteriormente, en el bootstrap uniforme se emplea como aproximación la distribución empírica (ver Sección A.1.2): \[F_n\left( x \right) =\frac{1}{n}\sum_{i=1}^{n}\mathbf{1}\left\{ X_i\leq x\right\}.\] Es decir, \(\hat{F}=F_n\), y por tanto \(R^{\ast}=R\left( \mathbf{X}^{\ast},F_n \right)\). En raras ocasiones (e.g. Sección 1.3 de Cao y Fernández-Casal, 2020) es posible calcular exactamente la distribución bootstrap de \(R^{\ast}\). Normalmente se aproxima esa distribución mediante Monte Carlo, generando una gran cantidad, \(B\), de réplicas de \(R^{\ast}\). En el caso del bootstrap uniforme, el algoritmo es:
Para cada \(i=1,\ldots ,n\) generar \(X_i^{\ast}\) a partir de \(F_n\), es decir \(P^{\ast}\left( X_i^{\ast}=X_j \right) =\frac{1}{n}\), \(j=1,\ldots,n\)
Obtener \(\mathbf{X}^{\ast}=\left( X_1^{\ast},\ldots ,X_n^{\ast} \right)\)
Calcular \(R^{\ast}=R\left( \mathbf{X}^{\ast},F_n \right)\)
Repetir \(B\) veces los pasos 1-3 para obtener las réplicas bootstrap \(R^{\ast (1)}, \ldots, R^{\ast (B)}\)
Utilizar esas réplicas bootstrap para aproximar la distribución en el muestreo de \(R\).
Para la elección del número de réplicas Monte Carlo \(B\) se aplicarían las mismas recomendaciones de la Sección 3.2 para el caso general de una aproximación por simulación.
Como ya se mostró anteriormente, el paso 1 se puede llevar a cabo simulando una distribución uniforme discreta mediante el método de la transformación cuantil (Sección 5.5):
- Para cada \(i=1,\ldots ,n\) arrojar \(U_i\sim \mathcal{U}\left( 0,1 \right)\) y hacer \(X_i^{\ast}=X_{\left\lfloor nU_i\right\rfloor +1}\)
Aunque en R es recomendable27 emplear la función sample para generar muestras aleatorias con reemplazamiento del conjunto de datos original:
muestra_boot <- sample(muestra, replace = TRUE)Ejemplo 8.2 (Inferencia sobre la media con varianza desconocida)
Como ejemplo consideramos la muestra de tiempos de vida de microorganismos lifetimes del paquete simres:
library(simres)
muestra <- lifetimes
summary(muestra)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.1430 0.2650 0.6110 0.8053 1.1200 2.0800hist(muestra)
rug(muestra)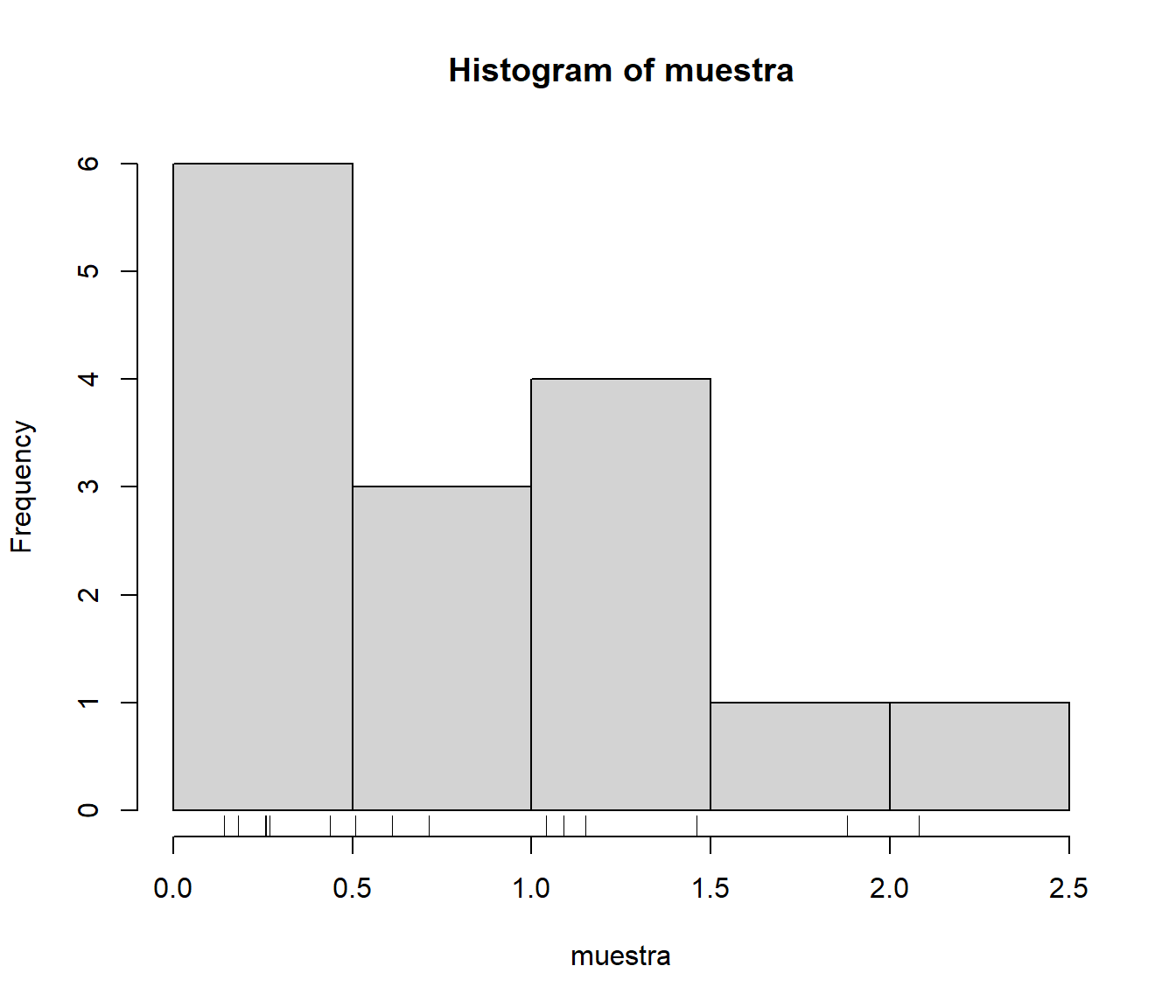
Figura 8.6: Distribución del tiempo de vida de una muestra de microorganismos.
Supongamos que queremos obtener una estimación por intervalo de confianza de su vida media a partir de los 15 valores observados mediante bootstrap uniforme considerando el estadístico \[R=R\left( \mathbf{X},F \right) =\sqrt{n}\frac{\bar{X}-\mu }{S_{n-1}},\] (en la Sección Sección ?? se tratará con más detalle la construcción de intervalos de confianza).
En el bootstrap uniforme se emplea \(\hat{F}=F_n\,\), con lo cual el análogo bootstrap del estadístico \(R\) será \[R^{\ast}=R\left( \mathbf{X}^{\ast},F_n \right) =\sqrt{n}\frac{\bar{X}^{\ast}-\bar{X}}{S_{n-1}^{\ast}},\] siendo \[\begin{aligned} \bar{X}^{\ast} &= \frac{1}{n}\sum_{i=1}^{n}X_i^{\ast}, \\ S_{n-1}^{\ast 2} &= \frac{1}{n-1}\sum_{i=1}^{n}\left( X_i^{\ast}- \bar{X}^{\ast} \right)^2. \end{aligned}\]
El algoritmo bootstrap (aproximado por Monte Carlo) procedería así:
Para cada \(i=1,\ldots ,n\) arrojar \(U_i\sim \mathcal{U}\left( 0,1 \right)\) y hacer \(X_i^{\ast}=X_{\left\lfloor nU_i\right\rfloor +1}\)
Obtener \(\bar{X}^{\ast}\) y \(S_{n-1}^{\ast 2}\)
Calcular \(R^{\ast}=\sqrt{n}\frac{\bar{X}^{\ast}-\bar{X}}{ S_{n-1}^{\ast}}\)
Repetir \(B\) veces los pasos 1-3 para obtener las réplicas bootstrap \(R^{\ast (1)}, \ldots, R^{\ast (B)}\)
Aproximar la distribución en el muestreo de \(R\) mediante la distribución empírica de \(R^{\ast (1)}, \ldots, R^{\ast (B)}\)
Por ejemplo, podríamos emplear el siguiente código:
n <- length(muestra)
alfa <- 0.05
# Estimaciones muestrales
x_barra <- mean(muestra)
cuasi_dt <- sd(muestra)
# Remuestreo
set.seed(1)
B <- 1000
estadistico_boot <- numeric(B)
for (k in 1:B) {
remuestra <- sample(muestra, n, replace = TRUE)
x_barra_boot <- mean(remuestra)
cuasi_dt_boot <- sd(remuestra)
estadistico_boot[k] <- sqrt(n) * (x_barra_boot - x_barra)/cuasi_dt_boot
}Las características de interés de la distribución en el muestreo de \(R\) se aproximan por las correspondientes de la distribución bootstrap de \(R^{\ast}\). En este caso nos interesa aproximar los puntos críticos \(x_{\alpha /2}\) y \(x_{1-\alpha /2}\), tales que: \[P\left( x_{\alpha /2} < R < x_{1-\alpha /2} \right) = 1-\alpha.\] Para lo que podemos emplear los cuantiles muestrales28:
pto_crit <- quantile(estadistico_boot, c(alfa/2, 1 - alfa/2))
pto_crit## 2.5% 97.5%
## -3.002197 1.877302A partir de los cuales obtenemos la correspondiente estimación por IC boostrap (ver Sección ??): \[\hat{IC}^{boot}_{1-\alpha}\left( \mu\right) = \left( \overline{X}-x_{1-\alpha/2}\dfrac{S_{n-1}}{\sqrt{n}},\ \overline{X} - x_{\alpha/2}\dfrac{S_{n-1}}{\sqrt{n}} \right).\]
ic_inf_boot <- x_barra - pto_crit[2] * cuasi_dt/sqrt(n)
ic_sup_boot <- x_barra - pto_crit[1] * cuasi_dt/sqrt(n)
IC_boot <- c(ic_inf_boot, ic_sup_boot)
names(IC_boot) <- paste0(100*c(alfa/2, 1-alfa/2), "%")
IC_boot## 2.5% 97.5%
## 0.5030131 1.2888063Este procedimiento para la construcción de intervalos de confianza se denomina método percentil-t y se tratará en la Sección ??.
Como ejemplo adicional podemos comparar la aproximación de la distribución bootstrap del estadístico con la aproximación \(t_{n-1}\) basada en normalidad.
hist(estadistico_boot, freq = FALSE, ylim = c(0, 0.4))
abline(v = pto_crit, lty = 2)
curve(dt(x, n - 1), add = TRUE, col = "blue")
pto_crit_t <- qt(1 - alfa/2, n - 1)
abline(v = c(-pto_crit_t, pto_crit_t), col = "blue", lty = 2)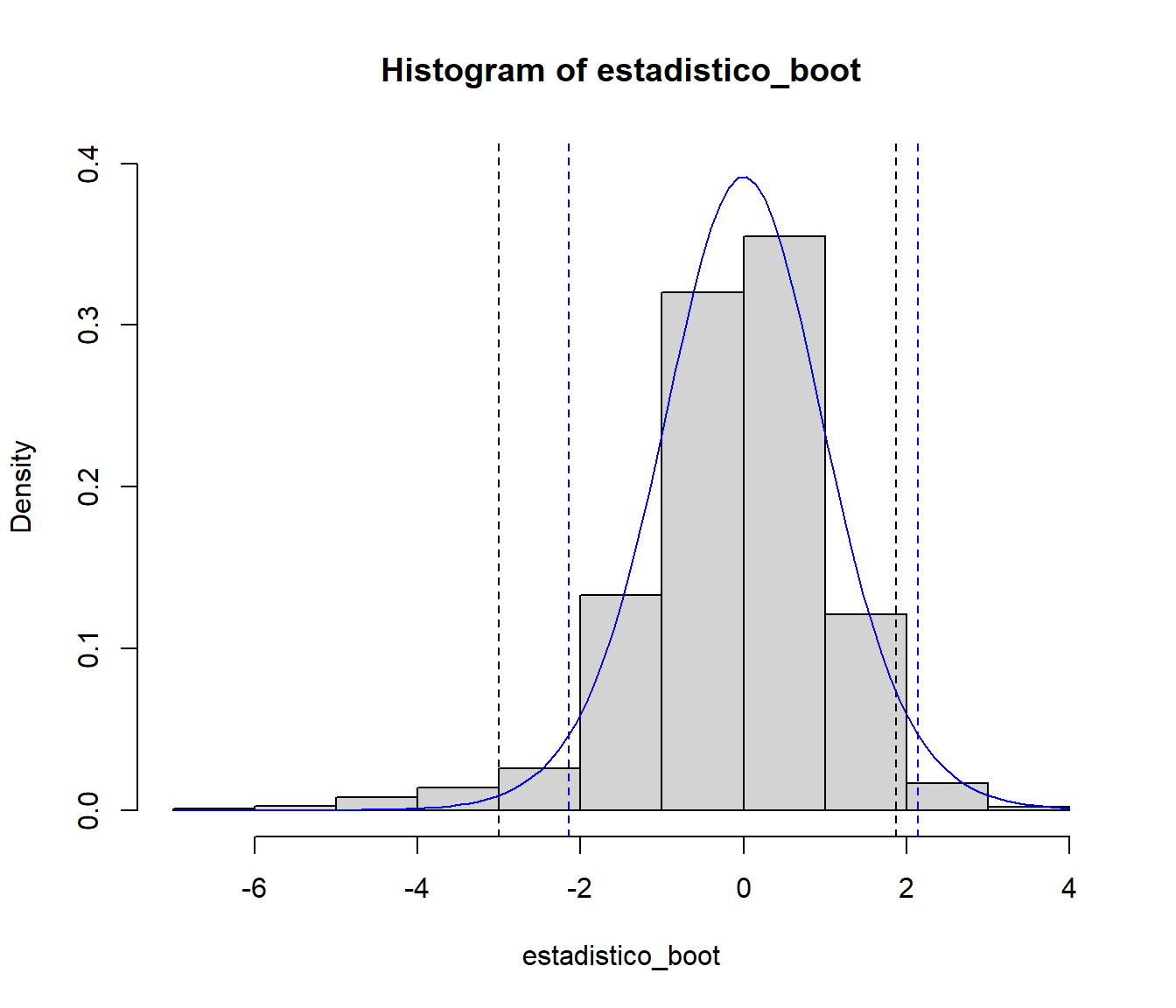
Figura 8.7: Aproximación de la distribución de la media muestral studentizada mediante bootstrap uniforme.
En este caso la distribución bootstrap del estadístico es más asimétrica, por lo que el intervalo de confianza no está centrado en la media,
al contrario que el obtenido con la aproximación tradicional.
Por ejemplo, podemos obtener la estimación basada en normalidad mediante la función t.test():
t.test(muestra)$conf.int## [1] 0.4599374 1.1507292
## attr(,"conf.level")
## [1] 0.95En el caso multidimensional, cuando trabajamos con un conjunto de datos con múltiples variables, podríamos emplear un procedimiento análogo, a partir de remuestras del vector de índices. Por ejemplo:
data(iris)
str(iris)## 'data.frame': 150 obs. of 5 variables:
## $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
## $ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
## $ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
## $ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
## $ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...n <- nrow(iris)
# i_boot <- floor(n*runif(n)) + 1
# i_boot <- sample.int(n, replace = TRUE)
i_boot <- sample(n, replace = TRUE)
data_boot <- iris[i_boot, ]
str(data_boot)## 'data.frame': 150 obs. of 5 variables:
## $ Sepal.Length: num 5.1 5.6 6.2 4.8 5.5 6.2 5.5 5.6 5 6.5 ...
## $ Sepal.Width : num 3.8 2.5 2.9 3.1 2.3 2.9 2.6 2.8 3.6 3 ...
## $ Petal.Length: num 1.9 3.9 4.3 1.6 4 4.3 4.4 4.9 1.4 5.8 ...
## $ Petal.Width : num 0.4 1.1 1.3 0.2 1.3 1.3 1.2 2 0.2 2.2 ...
## $ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 2 2 1 2 2 2 3 1 3 ...Esta forma de proceder es la que emplea por defecto el paquete boot que describiremos más adelante (Sección 8.3.1).
Ejercicio 8.1 (Bootstrap uniforme multidimensional)
Considerando el conjunto de datos Prestige del paquete carData, supongamos que queremos realizar inferencias sobre el coeficiente de correlación entre prestige (puntuación de ocupaciones obtenidas a partir de una encuesta) e income (media de ingresos en la ocupación).
Para ello podemos considerar el coeficiente de correlación lineal de Pearson:
\[\rho =\frac{ Cov \left( X, Y \right) }
{ \sigma \left( X \right) \sigma \left( Y \right) }\]
Su estimador es el coeficiente de correlación muestral:
\[r=\frac{\sum_{i=1}^{n}(x_i-\overline{x})(y_i-\overline{y})}
{\sqrt{ \sum_{i=1}^{n}(x_i-\overline{x})^{2}}
\sqrt{\sum_{i=1}^{n}(y_i-\overline{y})^{2}}},\]
que podemos calcular en R empleando la función cor():
data(Prestige, package = "carData")
# with(Prestige, cor(income, prestige))
cor(Prestige$income, Prestige$prestige)## [1] 0.7149057Para realizar inferencias sobre el coeficiente de correlación, como aproximación más simple, se puede considerar que la distribución muestral de \(r\) es aproximadamente normal de media \(\rho\) y varianza \[Var(r) \approx \frac{1 - \rho^2}{n - 2}.\]
Aproximar mediante bootstrap uniforme (multididimensional) la distribución del estadístico \(R = r -\rho\), empleando \(B=1000\) réplicas, y compararla con la aproximación normal, considerando \[\widehat{Var}(r) = \frac{1 - r^2}{n - 2}.\]
De esta forma se evitan posibles problemas numéricos al emplear el método de la transformación cuantil cuando \(n\) es extremadamente grande (e.g. https://stat.ethz.ch/pipermail/r-devel/2018-September/076817.html).↩︎
Se podrían considerar distintos estimadores del cuantil \(x_{\alpha}\) (ver p.e. la ayuda de la función
quantile()). Si empleamos directamente la distribución empírica, el cuantil se correspondería con la observación ordenada en la posición \(B \alpha\) (se suele hacer una interpolación lineal si este valor no es entero), lo que equivale a emplear la funciónquantile()deRcon el parámetrotype = 1. Esta función considera por defecto la posición \(1 + (B - 1) \alpha\) (type = 7). En el libro de Davison y Hinkley (1997), y en el paqueteboot, se emplea \((B + 1) \alpha\) (equivalente atype = 6; lo que justifica que consideren habitualmente 99, 199 ó 999 réplicas bootstrap).↩︎