9.1 Deficiencias del bootstrap uniforme

Como ya se comentó en la introducción, si el estadístico es función de los cuantiles muestrales el bootstrap uniforme puede no funcionar bien (por ejemplo en el caso de la mediana; ver Ejercicio 8.2). Esto es principalmente debido a que el conjunto de posibles valores de las réplicas bootstrap del estadístico puede ser muy pequeño (si el tamaño muestral es pequeño).

Un ejemplo en el que el bootstrap uniforme falla por completo es el caso del máximo de una distribución uniforme. Supongamos que la distribución poblacional, \(F\), es la \(\mathcal{U}\left( 0,\theta \right)\) y que estamos interesados en hacer inferencia sobre del parámetro \(\theta\) empleando su estimador máximo verosímil \(\hat{\theta}=X_{(n)}\), siendo \(\mathbf{X}=\left( X_1,X_2,\ldots ,X_n \right)\) la muestra observada. Para realizar dicha inferencia nos interesaría aproximar la distribución de \(R\left( \mathbf{X},F \right) =\hat{\theta}-\theta\).

La función de distribución en el muestreo, \(G\left( x \right)\), de \(\hat{\theta}\) puede calcularse de forma sencilla:

\[\begin{aligned} G\left( x \right) &= P\left( X_{\left( n \right)}\leq x \right) =P\left( X_i\leq x\,; 1 \leq i \leq n \right) \\ &= \prod_{i=1}^{n}P\left( X_i\leq x \right) =F\left( x \right)^{n}=\left( \frac{x}{\theta } \right)^{n},\text{ si }x\in \left[ 0,\theta \right]\end{aligned}\]

con lo cual su función de densidad viene dada por \[g\left( x \right) =\frac{n}{\theta }\left( \frac{x}{\theta } \right)^{n-1}, \text{ si }x\in \left[ 0,\theta \right] .\] Lo que confirma que \(\hat{\theta}\) es un estimador sesgado de \(\theta\), puesto que se tiene que \(\hat{\theta}\leq \theta\) con probabilidad 1. A partir de esta densidad podemos calcular fácilmente el sesgo del estimador: \[Sesgo\left( \hat{\theta} \right) =E\left( \hat{\theta} \right) -\theta = -\frac{\theta }{n+1}.\]

Si deseamos aproximar mediante bootstrap la distribución en el muestreo de \(\hat{\theta}\) (o la de \(R\)) y utilizamos un bootstrap uniforme (naïve), la versión bootstrap del estimador resulta ser \(\hat{\theta}^{\ast}=X_{(n)}^{\ast}\), siendo \(\mathbf{X}^{\ast}=\left(X_1^{\ast}\text{, }X_2^{\ast}\text{, }\ldots \text{, }X_n^{\ast} \right)\) una remuestra bootstrap obtenida a partir de la distribución empírica \(F_n\). La distribución en el remuestreo de \(\hat{\theta} ^{\ast}\,\) resulta un poco más complicada pues es discreta y sólo puede tomar cualquiera de los valores de la muestra.

Suponiendo que no hay empates en las observaciones de la muestra, es fácil darse cuenta de que \[P^{\ast}\left( \hat{\theta}^{\ast}\leq X_{(j)} \right) =P^{\ast}\left( X_{(n)}^{\ast}\leq X_{(j) } \right) =P^{\ast}\left( X_i^{\ast}\leq X_{(j)}\,; 1 \leq i \leq n \right) =\left( \frac{j}{n} \right)^{n}\] y, por tanto, su masa de probabilidad viene dada por \[P^{\ast}\left( \hat{\theta}^{\ast}=X_{(j)} \right) =\left( \frac{j}{n} \right)^{n}-\left( \frac{j-1}{n} \right)^{n}\text{, }j=1,\ldots,n.\]

En particular, \[P^{\ast}\left( \hat{\theta}^{\ast}=X_{(n)} \right) =1-\left( 1- \frac{1}{n} \right)^{n}\rightarrow 1-\frac{1}{e}\simeq 0.6321,\] con lo cual la distribución en remuestreo de \(R^{\ast}=R\left( \mathbf{X}^{\ast},F_n \right) =\hat{\theta}^{\ast}-X_{\left( n \right)}\) tiene un átomo de probabilidad en el valor \(0\) cuya probabilidad tiende a \(1-\frac{1}{e}\) cuando el tamaño muestral tiende a infinito, es decir

\[\lim_{n\rightarrow \infty }P^{\ast}\left( R^{\ast}=0 \right) =1-\frac{1}{e},\]

algo que no ocurre con la distribución en el muestreo de \(R\), que es continua con densidad: \[g_R\left( x \right) =\frac{n}{\theta }\left( \frac{x + \theta}{\theta } \right)^{n-1}, \text{ si }x\in \left[ -\theta, 0\right].\] De esta forma vemos que el bootstrap uniforme (no paramétrico) es inconsistente.

Ejemplo 9.1 (Inferencia sobre el máximo de una distribución uniforme)

El siguiente código implementa el método bootstrap uniforme (también llamado naïve) para aproximar la distribución del estadístico \(R=\hat{\theta}-\theta\), para una muestra de tamaño \(n=50\), proveniente de una población con distribución \(\mathcal{U}\left( 0,1\right)\) :

theta <- 1
n <- 50
set.seed(1)
muestra <- runif(50) * theta
theta_est <- max(muestra)
# Remuestreo
B <- 2000
maximo <- numeric(B)
estadistico <- numeric(B)
for (k in 1:B) {
    remuestra <- sample(muestra, n, replace = TRUE)
    maximo[k] <- max(remuestra)
    estadistico[k] <- maximo[k] - theta_est
}
# Distribución estadístico
xlim <- c(-theta/2, 0) # c(-theta, 0)
hist(estadistico, freq = FALSE, main = "", breaks = "FD",  
     border = "darkgray", xlim = xlim)
lines(density(estadistico))
rug(estadistico, col = "darkgray")
curve(n/theta * ((x + theta)/theta)^(n - 1), col = "blue", lty = 2, lwd = 2, add = TRUE)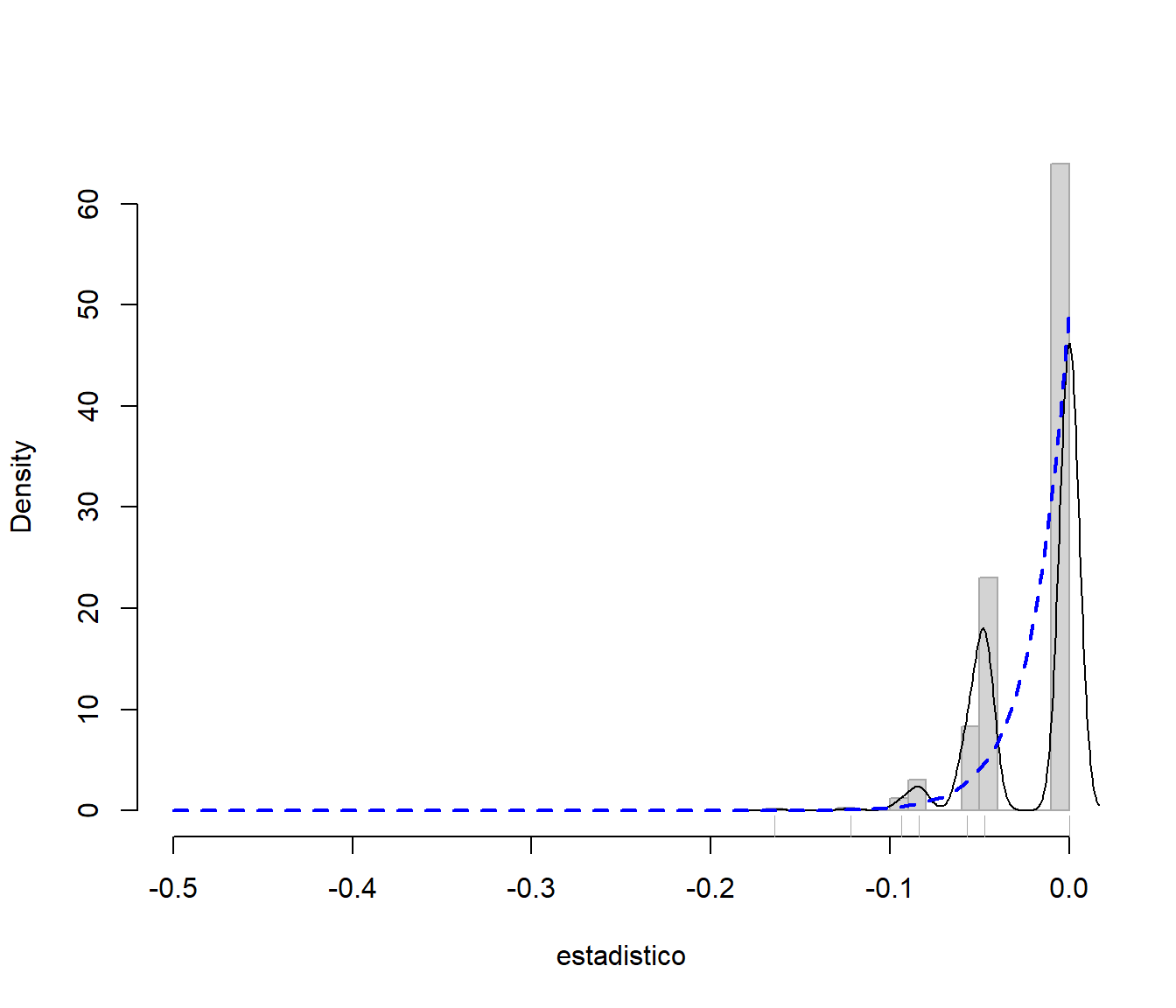

Figura 9.1: Distribución de las réplicas bootstrap (uniforme) del estadístico y distribución poblacional.

Este problema podría evitarse empleando el bootstrap paramétrico descrito a continuación (ver Ejemplo 9.3).