2.3 Análisis de la calidad de un generador

Para verificar si un generador tiene las propiedades estadísticas deseadas hay disponibles una gran cantidad de test de hipótesis y métodos gráficos, incluyendo métodos genéricos (de bondad de ajuste y aleatoriedad) y contrastes específicos para generadores aleatorios. Se trata principalmente de contrastar si las muestras generadas son i.i.d. \(\mathcal{U}\left(0,1\right)\) (análisis univariante). Aunque los métodos más avanzados tratan de contrastar si las \(d\)-uplas:

\[(U_{t+1},U_{t+2},\ldots,U_{t+d}); \ t=(i-1)d, \ i=1,\ldots,m\]

son i.i.d. \(\mathcal{U}\left(0,1\right)^{d}\) (uniformes independientes en el hipercubo; análisis multivariante). En el Apéndice A se describen algunos de estos métodos.

En esta sección emplearemos únicamente métodos genéricos, ya que también pueden ser de utilidad para evaluar generadores de variables no uniformes y para la construcción de modelos del sistema real (e.g. para modelar variables que se tratarán como entradas del modelo general). Sin embargo, los métodos clásicos pueden no ser muy adecuados para evaluar generadores de números pseudoaleatorios (ver L’Ecuyer y Simard, 2007). La recomendación sería emplear baterías de contrastes recientes, como las descritas en la Subsección 2.3.2.

Hay que destacar algunas diferencias entre el uso de este tipo de métodos en inferencia y en simulación. Por ejemplo, si empleamos un constrate de hipótesis del modo habitual, desconfiamos del generador si la muestra (secuencia) no se ajusta a la distribución teórica (p-valor \(\leq \alpha\)). En simulación, además, también se sospecha si se ajusta demasiado bien a la distribución teórica (p-valor \(\geq1-\alpha\)), lo que indicaría que no reproduce adecuadamente la variabilidad.

Uno de los contrastes más conocidos es el test chi-cuadrado de bondad de ajuste (chisq.test para el caso discreto). Aunque si la variable de interés es continua, habría que discretizarla (con la correspondiente perdida de información). Por ejemplo, se podría emplear la función simres::chisq.cont.test() (fichero test.R), que imita a las incluidas en R:

simres::chisq.cont.test

## function(x, distribution = "norm", nclass = floor(length(x)/5),
##                             output = TRUE, nestpar = 0, ...) {
##   # Función distribución
##   q.distrib <- eval(parse(text = paste("q", distribution, sep = "")))
##   # Puntos de corte
##   q <- q.distrib((1:(nclass - 1))/nclass, ...)
##   tol <- sqrt(.Machine$double.eps)
##   xbreaks <- c(min(x) - tol, q, max(x) + tol)
##   # Gráficos y frecuencias
##   if (output) {
##     xhist <- hist(x, breaks = xbreaks, freq = FALSE,
##                   lty = 2, border = "grey50")
##     # Función densidad
##     d.distrib <- eval(parse(text = paste("d", distribution, sep = "")))
##     curve(d.distrib(x, ...), add = TRUE)
##   } else {
##     xhist <- hist(x, breaks = xbreaks, plot = FALSE)
##   }
##   # Cálculo estadístico y p-valor
##   O <- xhist$counts  # Equivalente a table(cut(x, xbreaks)) pero más eficiente
##   E <- length(x)/nclass
##   DNAME <- deparse(substitute(x))
##   METHOD <- "Pearson's Chi-squared test"
##   STATISTIC <- sum((O - E)^2/E)
##   names(STATISTIC) <- "X-squared"
##   PARAMETER <- nclass - nestpar - 1
##   names(PARAMETER) <- "df"
##   PVAL <- pchisq(STATISTIC, PARAMETER, lower.tail = FALSE)
##   # Preparar resultados
##   classes <- format(xbreaks)
##   classes <- paste("(", classes[-(nclass + 1)], ",", classes[-1], "]",
##                    sep = "")
##   RESULTS <- list(classes = classes, observed = O, expected = E,
##                   residuals = (O - E)/sqrt(E))
##   if (output) {
##     cat("\nPearson's Chi-squared test table\n")
##     print(as.data.frame(RESULTS))
##   }
##   if (any(E < 5))
##     warning("Chi-squared approximation may be incorrect")
##   structure(c(list(statistic = STATISTIC, parameter = PARAMETER, p.value = PVAL,
##                    method = METHOD, data.name = DNAME), RESULTS), class = "htest")
## }
## <bytecode: 0x0000000038ca9808>
## <environment: namespace:simres>

Ejemplo 2.2 (análisis de un generador congruencial continuación)

Continuando con el generador congruencial del Ejemplo 2.1:

set.rng(321, "lcg", a = 5, c = 1, m = 512)  # Establecer semilla y parámetros
nsim <- 500
u <- rng(nsim)

Al aplicar el test chi-cuadrado obtendríamos:

chisq.cont.test(u, distribution = "unif", 
                nclass = 10, nestpar = 0, min = 0, max = 1)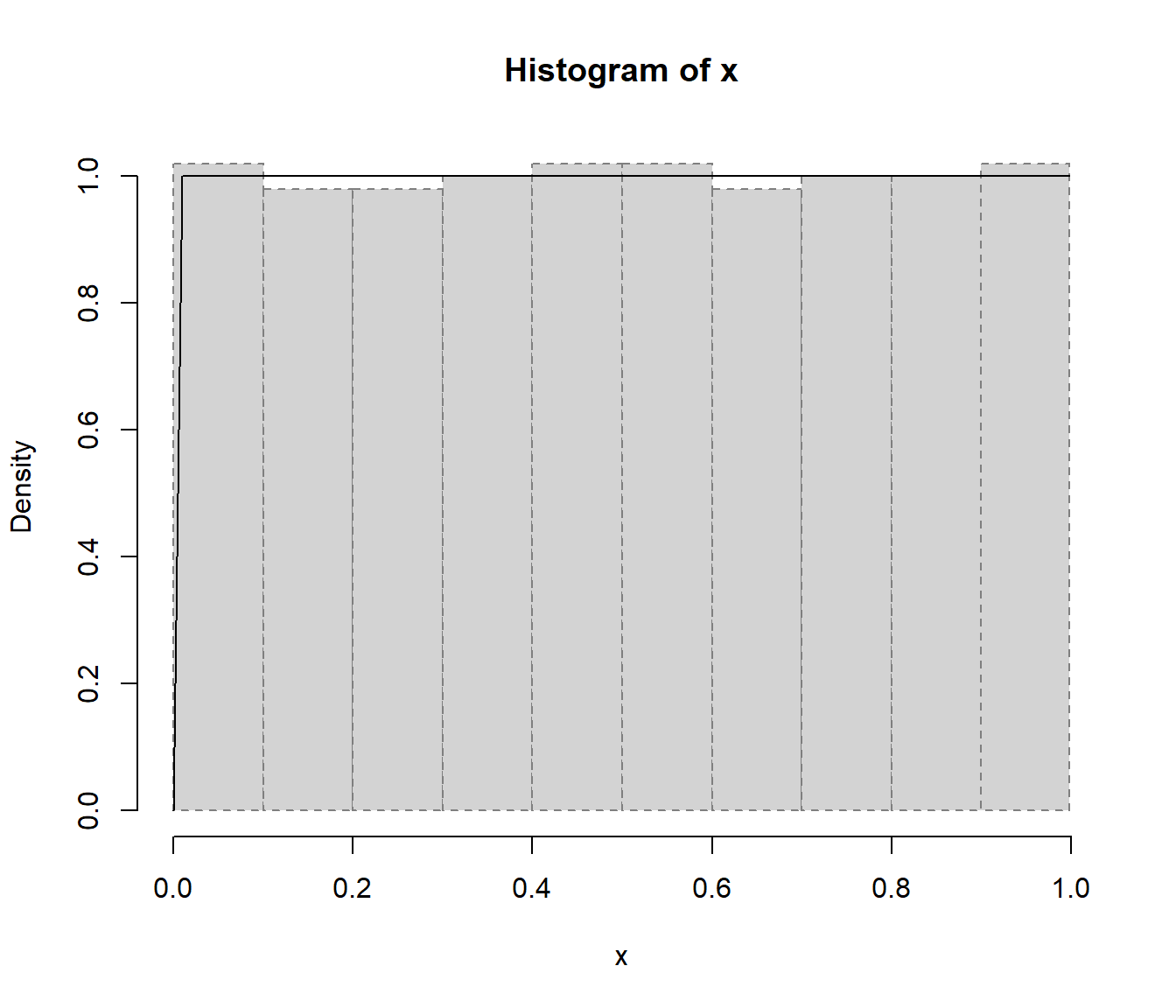

Figura 2.3: Gráfico resultante de aplicar la función chisq.cont.test() comparando el histograma de los valores generados con la densidad uniforme.

## 
## Pearson's Chi-squared test table
##                          classes observed expected  residuals
## 1  (-1.490116e-08, 1.000000e-01]       51       50  0.1414214
## 2  ( 1.000000e-01, 2.000000e-01]       49       50 -0.1414214
## 3  ( 2.000000e-01, 3.000000e-01]       49       50 -0.1414214
## 4  ( 3.000000e-01, 4.000000e-01]       50       50  0.0000000
## 5  ( 4.000000e-01, 5.000000e-01]       51       50  0.1414214
## 6  ( 5.000000e-01, 6.000000e-01]       51       50  0.1414214
## 7  ( 6.000000e-01, 7.000000e-01]       49       50 -0.1414214
## 8  ( 7.000000e-01, 8.000000e-01]       50       50  0.0000000
## 9  ( 8.000000e-01, 9.000000e-01]       50       50  0.0000000
## 10 ( 9.000000e-01, 9.980469e-01]       50       50  0.0000000

## 
##  Pearson's Chi-squared test
## 
## data:  u
## X-squared = 0.12, df = 9, p-value = 1

Alternativamente, por ejemplo si solo se pretende aplicar el contraste, se podría emplear la función simres::freq.test() (fichero test.R) para este caso particular (ver Sección A.3.1).

Como se muestra en la Figura 2.3 el histograma de la secuencia generada es muy plano (comparado con lo que cabría esperar de una muestra de tamaño 500 de una uniforme), y consecuentemente el p-valor del contraste chi-cuadrado es prácticamente 1, lo que indicaría que este generador no reproduce adecuadamente la variabilidad de una distribución uniforme.

Otro contraste de bondad de ajuste muy conocido es el test de Kolmogorov-Smirnov, implementado en ks.test (ver Sección A.1.5). Este contraste de hipótesis compara la función de distribución bajo la hipótesis nula con la función de distribución empírica (ver Sección A.1.2), representadas en la Figura 2.4:

# Distribución empírica
curve(ecdf(u)(x), type = "s", lwd = 2)
curve(punif(x, 0, 1), add = TRUE)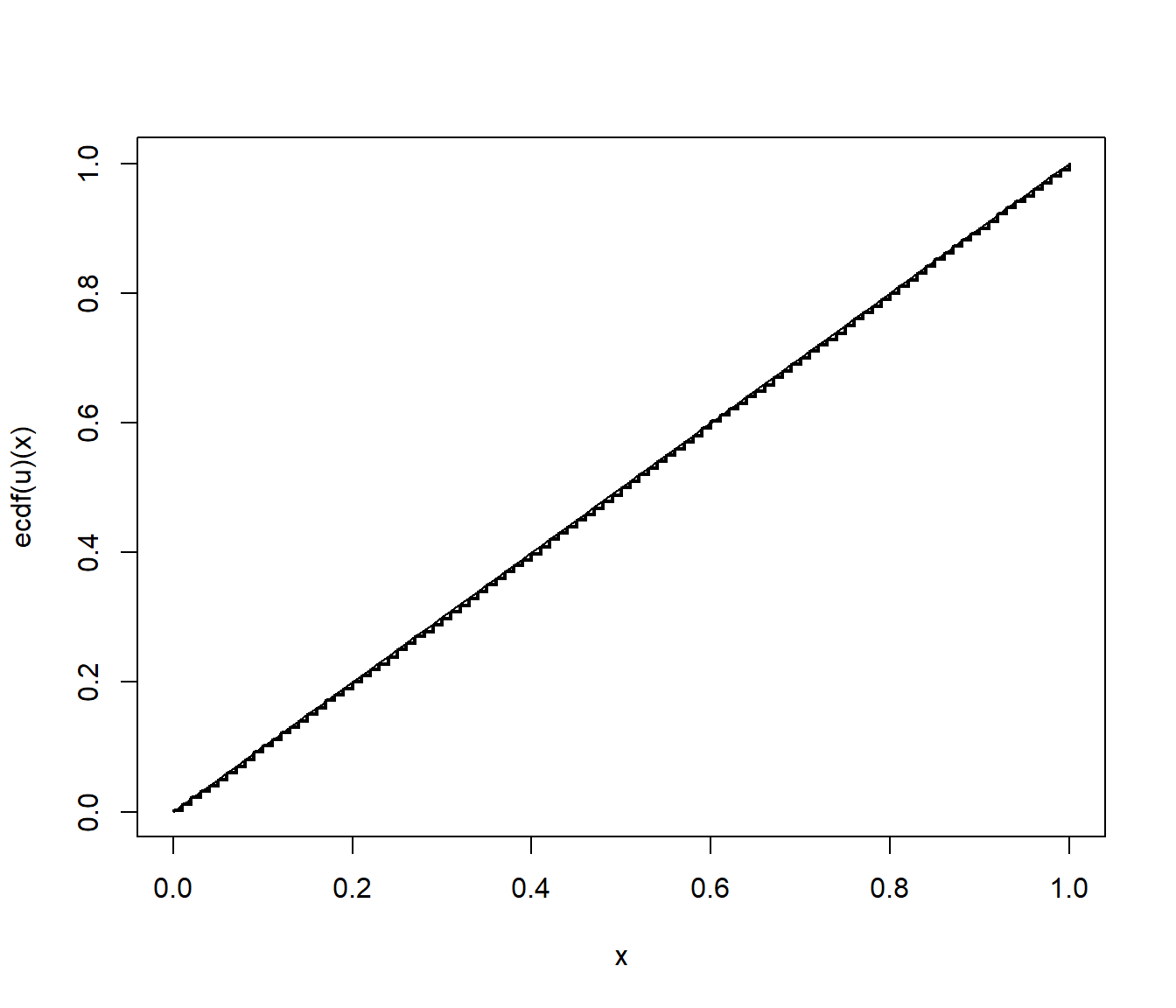

Figura 2.4: Comparación de la distribución empírica de la secuencia generada con la función de distribución uniforme.

Podemos realizar el contraste con el siguiente código:

# Test de Kolmogorov-Smirnov
ks.test(u, "punif", 0, 1)

## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  u
## D = 0.0033281, p-value = 1
## alternative hypothesis: two-sided

En la Sección A.1 se describen con más detalle estos contrastes de bondad de ajuste.

Adicionalmente podríamos estudiar la aleatoriedad de los valores generados (ver Sección A.2), por ejemplo mediante un gráfico secuencial y el de dispersión retardado.

plot(as.ts(u))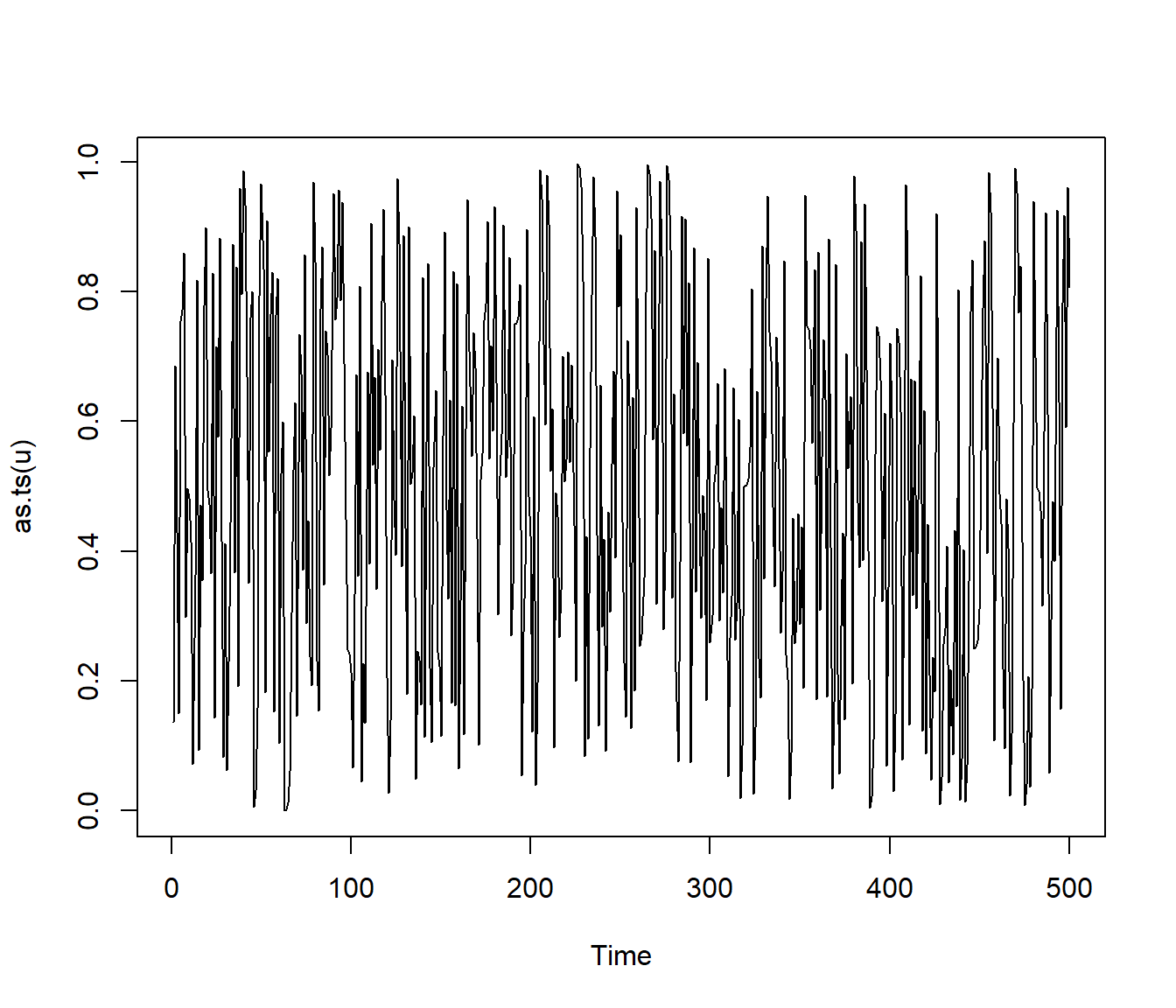

Figura 2.5: Gráfico secuencial de los valores generados.

plot(u[-nsim],u[-1])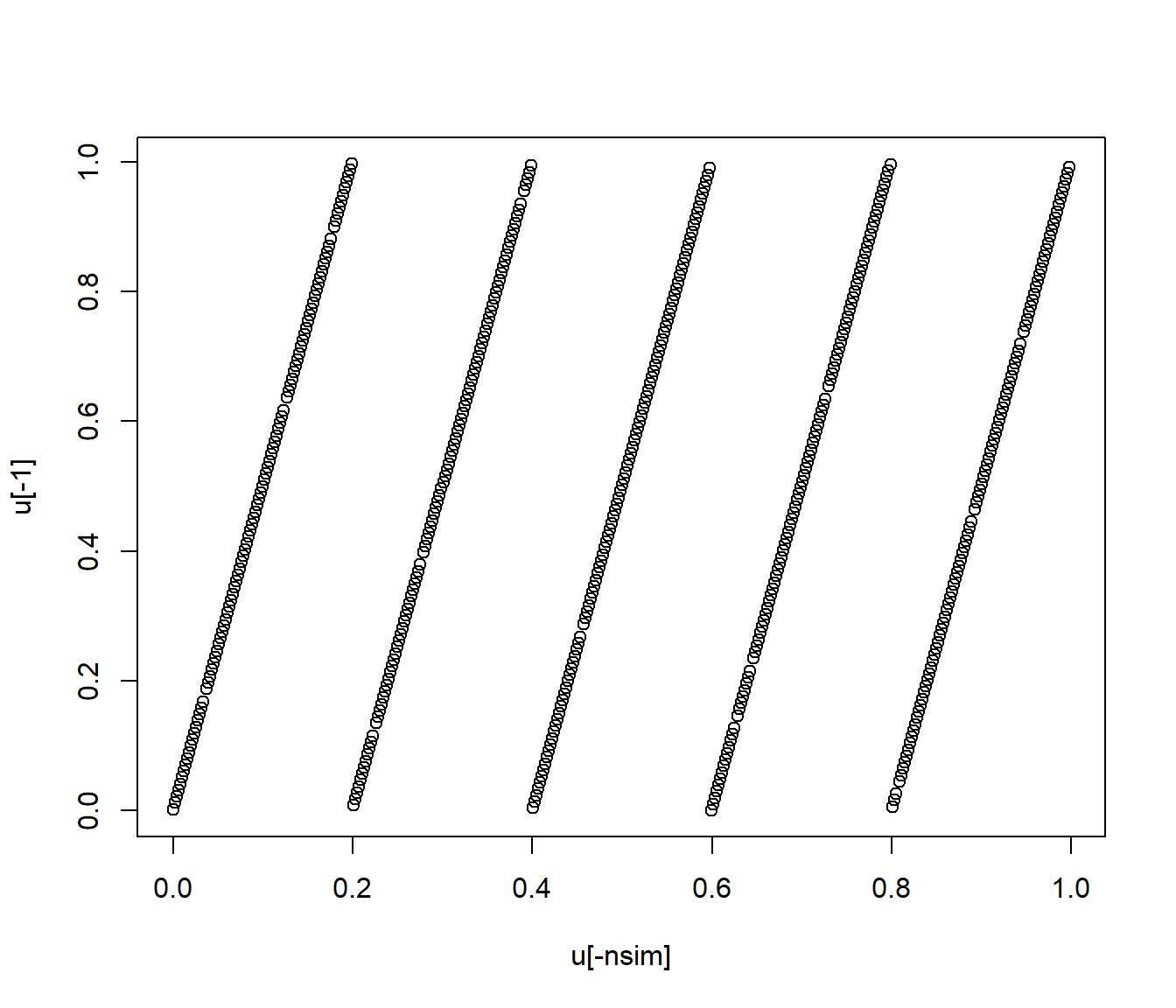

Figura 2.6: Gráfico de dispersión retardado de los valores generados.

Si se observa algún tipo de patrón indicaría dependencia (se podría considerar como una versión descriptiva del denominado “Parking lot test”), ver Ejemplo A.2.

También podemos analizar las autocorrelaciones (las correlaciones de \((u_{i},u_{i+k})\), con \(k=1,\ldots,K\)):

acf(u)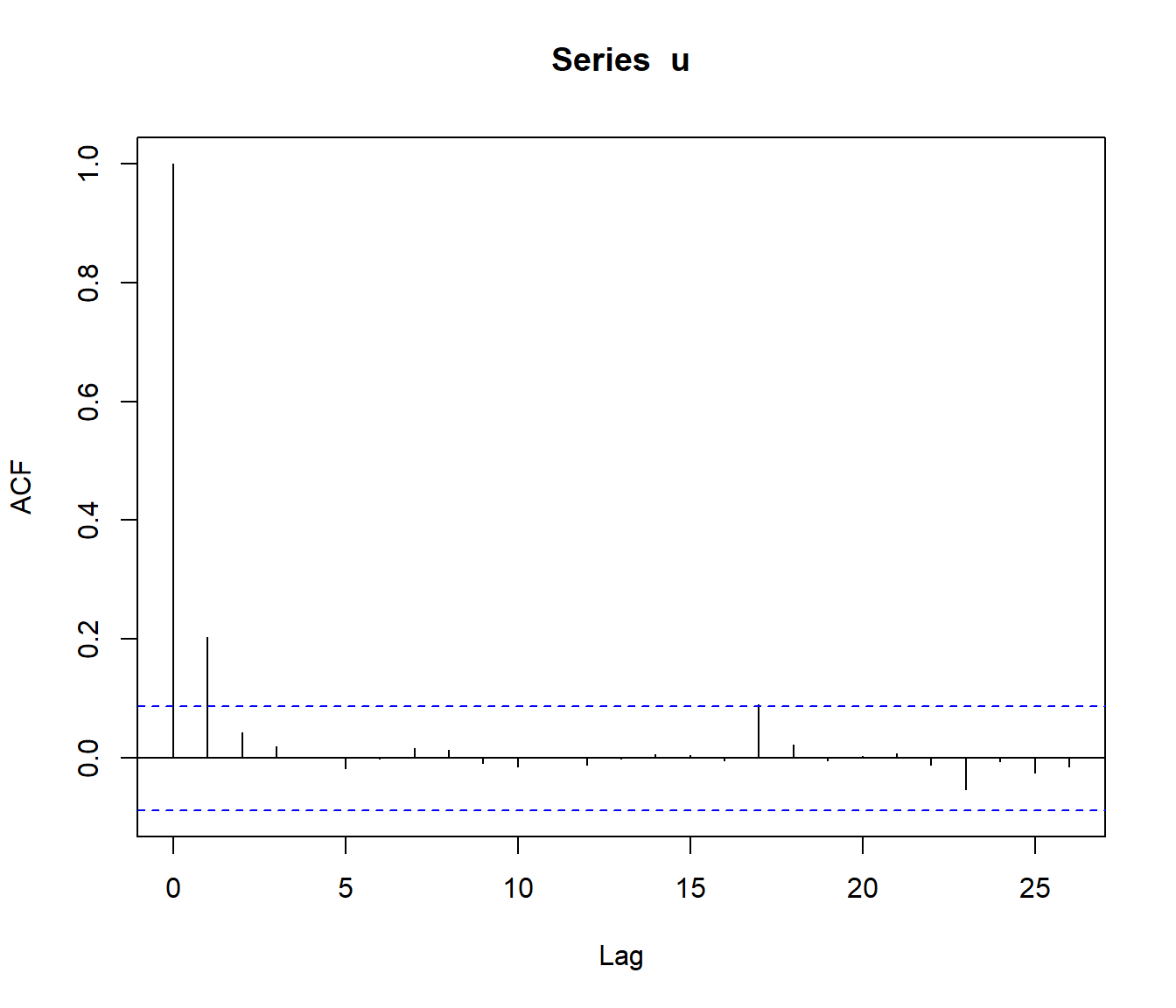

Figura 2.7: Autocorrelaciones de los valores generados.

Por ejemplo, para contrastar si las diez primeras autocorrelaciones son nulas podríamos emplear el test de Ljung-Box:

Box.test(u, lag = 10, type = "Ljung")

## 
##  Box-Ljung test
## 
## data:  u
## X-squared = 22.533, df = 10, p-value = 0.01261

2.3.1 Repetición de contrastes

Los contrastes se plantean habitualmente desde el punto de vista de la inferencia estadística: se realiza una prueba sobre la única muestra disponible. Si se realiza una única prueba, en las condiciones de \(H_0\) hay una probabilidad \(\alpha\) de rechazarla. En simulación tiene mucho más sentido realizar un gran número de pruebas:

La proporción de rechazos debería aproximarse al valor de \(\alpha\) (se puede comprobar para distintos valores de \(\alpha\)).
La distribución del estadístico debería ajustarse a la teórica bajo \(H_0\) (se podría realizar un nuevo contraste de bondad de ajuste).
Los p-valores obtenidos deberían ajustarse a una \(\mathcal{U}\left(0,1\right)\) (se podría realizar también un contraste de bondad de ajuste).

Este procedimiento es también el habitual para validar un método de contraste de hipótesis por simulación (ver Sección 7.4.3).

Ejemplo 2.3

Continuando con el generador congruencial RANDU, podemos pensar en estudiar la uniformidad de los valores generados empleando repetidamente el test chi-cuadrado:

# Valores iniciales
set.rng(543210, "lcg", a = 2^16 + 3, c = 0, m = 2^31)  # Establecer semilla y parámetros
# set.seed(543210)
n <- 500
nsim <- 1000
estadistico <- numeric(nsim)
pvalor <- numeric(nsim)

# Realizar contrastes
for(isim in 1:nsim) {
  u <- rng(n)    # Generar
  # u <- runif(n)
  tmp <- freq.test(u, nclass = 100)
  # tmp <- chisq.cont.test(u, distribution = "unif", nclass = 100, 
  #     output = FALSE, nestpar = 0, min = 0, max = 1)
  estadistico[isim] <- tmp$statistic
  pvalor[isim] <- tmp$p.value
}

Por ejemplo, podemos comparar la proporción de rechazos observados con los que cabría esperar con los niveles de significación habituales:

{
cat("Proporción de rechazos al 1% =", mean(pvalor < 0.01), "\n") # sum(pvalor < 0.01)/nsim
cat("Proporción de rechazos al 5% =", mean(pvalor < 0.05), "\n")   # sum(pvalor < 0.05)/nsim
cat("Proporción de rechazos al 10% =", mean(pvalor < 0.1), "\n")   # sum(pvalor < 0.1)/nsim
}

## Proporción de rechazos al 1% = 0.014 
## Proporción de rechazos al 5% = 0.051 
## Proporción de rechazos al 10% = 0.112

Las proporciones de rechazo obtenidas deberían comportarse como una aproximación por simulación de los niveles teóricos. En este caso no se observa nada extraño, por lo que no habría motivos para sospechar de la uniformidad de los valores generados (aparentemente no hay problemas con la uniformidad de este generador).

Adicionalmente, si queremos estudiar la proporción de rechazos (el tamaño del contraste) para los posibles valores de \(\alpha\), podemos emplear la distribución empírica del p-valor (proporción de veces que resultó menor que un determinado valor):

# Distribución empírica
plot(ecdf(pvalor), do.points = FALSE, lwd = 2, 
     xlab = 'Nivel de significación', ylab = 'Proporción de rechazos')
abline(a = 0, b = 1, lty = 2)   # curve(punif(x, 0, 1), add = TRUE)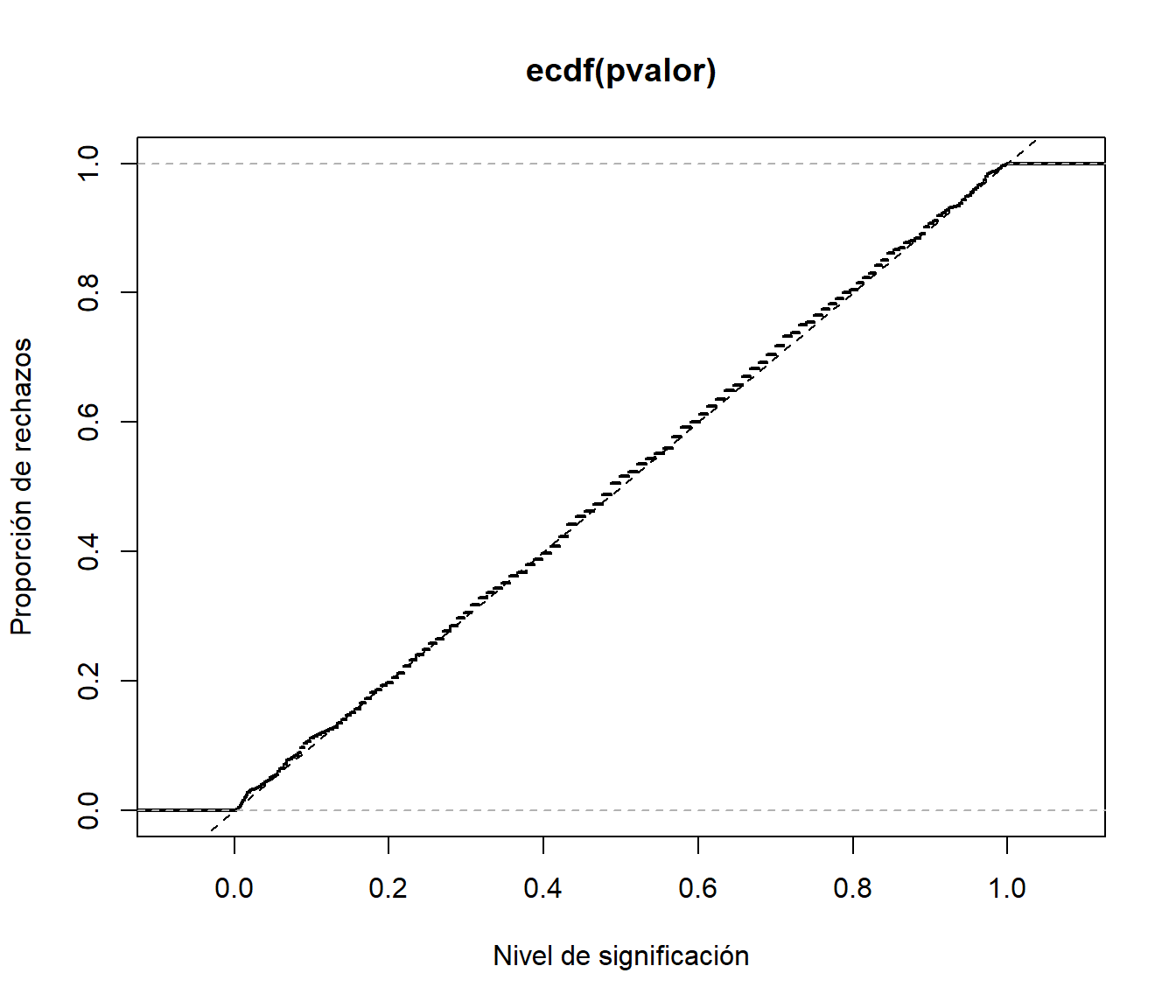

Figura 2.8: Proporción de rechazos con los distintos niveles de significación.

También podemos estudiar la distribución del estadístico del contraste. En este caso, como la distribución bajo la hipótesis nula está implementada en R, podemos compararla fácilmente con la de los valores generados (debería ser una aproximación por simulación de la distribución teórica):

# Histograma
hist(estadistico, breaks = "FD", freq = FALSE, main = "")
curve(dchisq(x, 99), add = TRUE)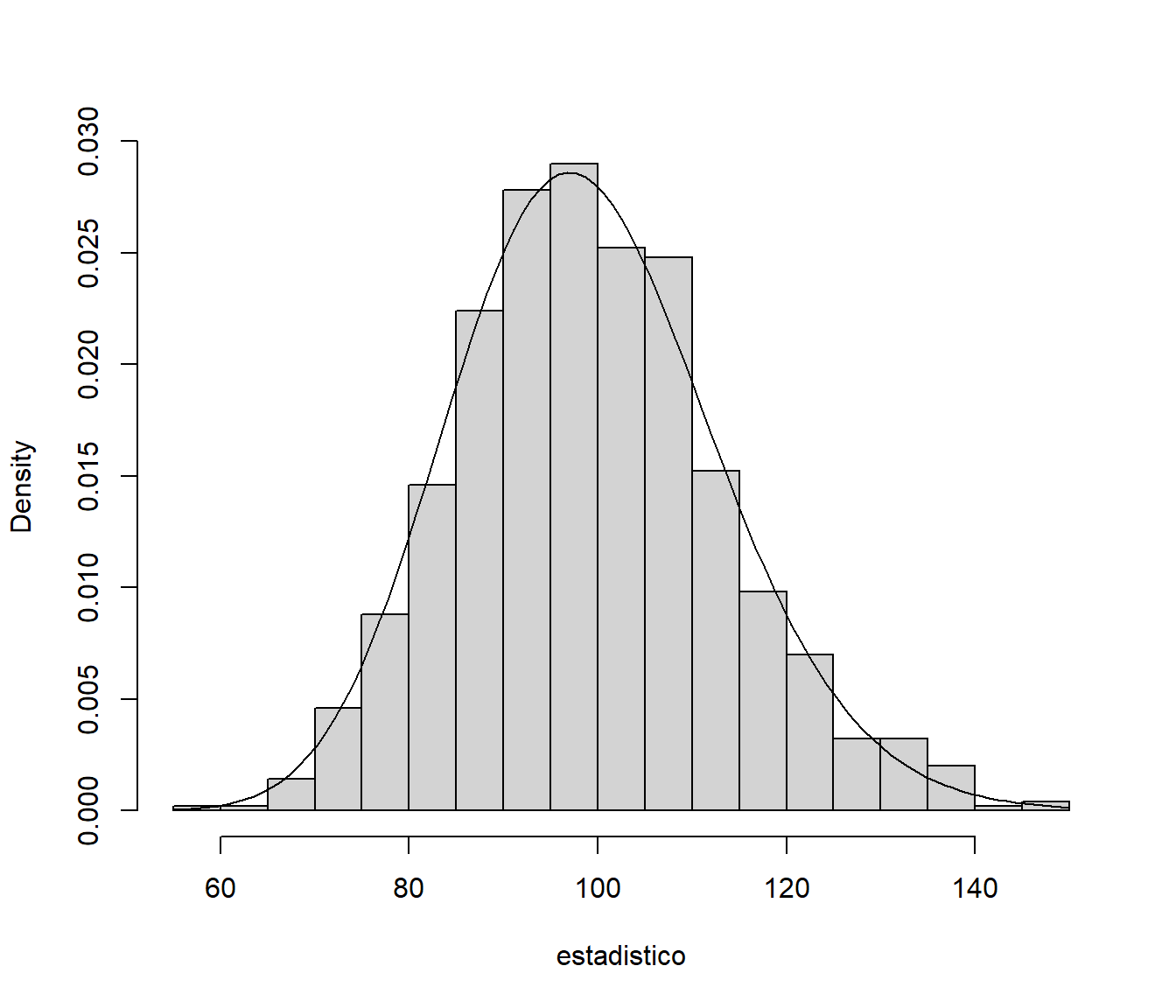

Figura 2.9: Distribución del estadístico del constraste.

Además de la comparación gráfica, podríamos emplear un test de bondad de ajuste para contrastar si la distribución del estadístico es la teórica bajo la hipótesis nula:

# Test chi-cuadrado (chi-cuadrado sobre chi-cuadrado)
# chisq.cont.test(estadistico, distribution="chisq", nclass=20, nestpar=0, df=99)
# Test de Kolmogorov-Smirnov
ks.test(estadistico, "pchisq", df = 99)

## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  estadistico
## D = 0.023499, p-value = 0.6388
## alternative hypothesis: two-sided

En este caso la distribución observada del estadístico es la que cabría esperar de una muestra de este tamaño de la distribución teórica, por tanto, según este criterio, aparentemente no habría problemas con la uniformidad de este generador (hay que recordar que estamos utilizando contrastes de hipótesis como herramienta para ver si hay algún problema con el generador, no tiene mucho sentido hablar de aceptar o rechazar una hipótesis).

En lugar de estudiar la distribución del estadístico de contraste siempre podemos analizar la distribución del p-valor. Mientras que la distribución teórica del estadístico depende del contraste y puede ser complicada, la del p-valor es siempre una uniforme.

# Histograma
hist(pvalor, freq = FALSE, main = "")
abline(h=1) # curve(dunif(x,0,1), add=TRUE)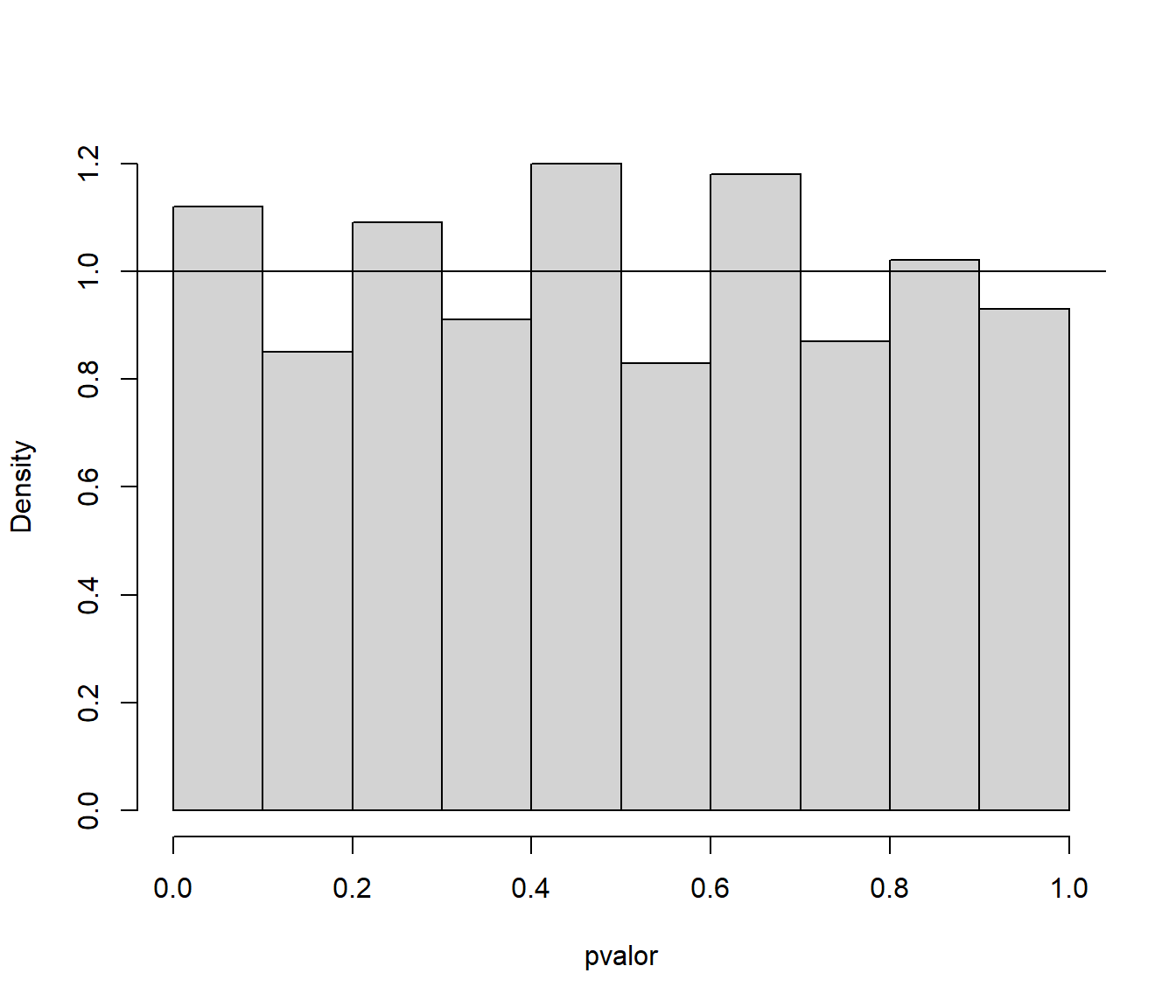

Figura 2.10: Distribución del p-valor del constraste.

# Test chi-cuadrado
# chisq.cont.test(pvalor, distribution="unif", nclass=20, nestpar=0, min=0, max=1)
# Test de Kolmogorov-Smirnov
ks.test(pvalor, "punif",  min = 0, max = 1)

## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  pvalor
## D = 0.023499, p-value = 0.6388
## alternative hypothesis: two-sided

Como podemos observar, obtendríamos los mismos resultados que al analizar la distribución del estadístico.

Alternativamente podríamos emplear la función rephtest() del paquete simres (fichero test.R):

set.rng(543210, "lcg", a = 2^16 + 3, c = 0, m = 2^31)
# res <- rephtest(n = 30, test = chisq.cont.test, rand.gen = rng,
#          distribution = "unif", output = FALSE, nestpar = 0)
res <- rephtest(n = 30, test = freq.test, rand.gen = rng, nclass = 6)
str(res)

## List of 2
##  $ statistics: num [1:1000] 5.2 6.8 12.4 0.8 5.6 7.6 6.4 9.6 5.2 3.2 ...
##  $ p.values  : num [1:1000] 0.392 0.2359 0.0297 0.977 0.3471 ...
##  - attr(*, "class")= chr "rhtest"
##  - attr(*, "method")= chr "Chi-squared test for given probabilities"
##  - attr(*, "names.stat")= chr "X-squared"
##  - attr(*, "parameter")= Named num 5
##   ..- attr(*, "names")= chr "df"

summary(res)

## Proportion of rejections:
##    1%    5%   10%   25%   50% 
## 0.013 0.054 0.096 0.255 0.544

old.par <- par(mfrow = c(1, 2))
plot(res, 2:3)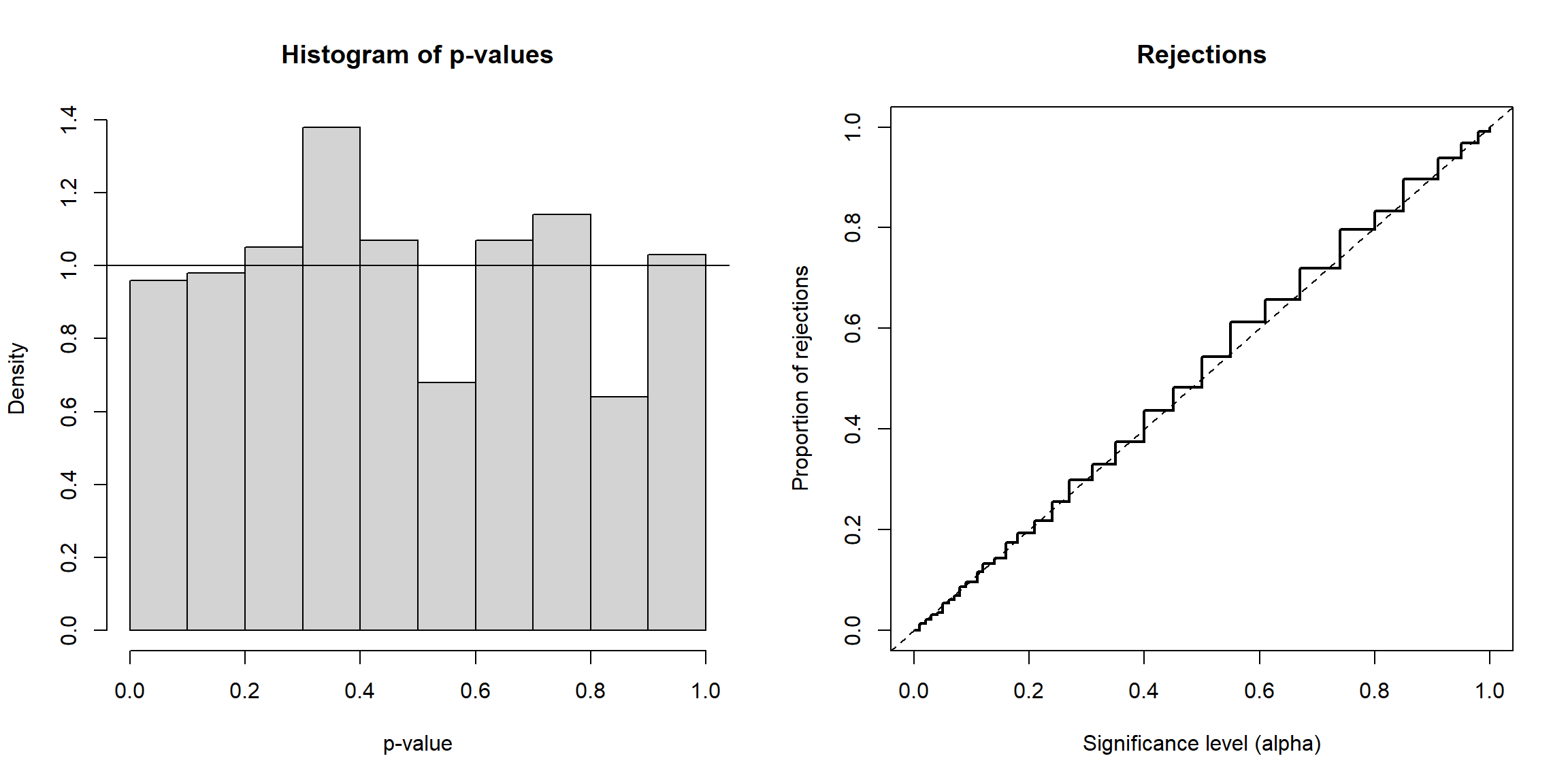

Figura 2.11: Distribución de los p-valores y proporción de rechazos.

par(old.par)

2.3.2 Baterías de contrastes

Hay numerosos ejemplos de generadores que pasaron diferentes test de uniformidad y aleatoriedad pero que fallaron estrepitosamente al considerar nuevos contrastes diseñados específicamente para generadores aleatorios (ver Marsaglia et al., 1990). Por este motivo, el procedimiento habitual en la práctica es aplicar un número más o menos elevado de contrastes (de distinto tipo y difíciles de pasar, e.g. Marsaglia y Tsang, 2002), de forma que si el generador los pasa tendremos mayor confianza en que sus propiedades son las adecuadas. Este conjunto de pruebas es lo que se denomina batería de contrastes. Una de las primeras se introdujo en Knuth (1969) y de las más recientes podríamos destacar:

Diehard tests (The Marsaglia Random Number CDROM, 1995): http://www.stat.fsu.edu/pub/diehard (versión archivada el 2016-01-25).
Dieharder (Brown y Bauer, 2003): Dieharder Page, paquete RDieHarder.
TestU01 (L’Ecuyer y Simard, 2007): http://simul.iro.umontreal.ca/testu01/tu01.html.
NIST test suite (National Institute of Standards and Technology, USA, 2010): http://csrc.nist.gov/groups/ST/toolkit/rng.

Para más detalles, ver por ejemplo⁹:

Marsaglia, G. y Tsang, W.W. (2002). Some difficult-to-pass tests of randomness. Journal of Statistical Software, 7(3), 1-9.
Demirhan, H. y Bitirim, N. (2016). CryptRndTest: an R package for testing the cryptographic randomness. The R Journal, 8(1), 233-247.

Estas baterías de contrastes se suelen emplear si el generador va a ser utilizado en criptografía o si es muy importante la impredecibilidad (normalmente con generadores de números “verdaderamente aleatorios” por hardware). Si el objetivo es únicamente obtener resultados estadísticos (como en nuestro caso) no sería tan importante que el generador no superase alguno de estos test.

También puede ser de interés el enlace Randomness Tests: A Literature Survey y la entidad certificadora (gratuita) en línea CAcert.↩︎