8.1 Introducción

En primer lugar nos centraremos en la idea original del bootstrap uniforme (Efron, 1979; también denominado bootstrap no paramétrico o naïve), que se expondrá de manera más formal en la Sección 8.2.

Supongamos que \(\mathbf{X}=\left( X_1,\ldots ,X_n \right)\) es una una muestra aleatoria simple (m.a.s.) de una población con distribución \(F_{\theta}\) y que estamos interesados en hacer inferencia sobre \(\theta\) empleando un estimador \(\hat{\theta} = T\left( \mathbf{X} \right)\).

La idea es aproximar características poblacionales por las correspondientes de la distribución empírica de los datos observados. Se trata de imitar el experimento de muestreo en la población real, pero empleando la distribución empírica en lugar de la distribución teórica \(F_{\theta}\) desconocida. Al conocer el mecanismo que genera los datos en el universo bootstrap, se puede emplear Monte Carlo para simularlo. En el caso i.i.d. esto puede ser implementado mediante remuestreo, realizando repetidamente muestreo aleatorio con reemplazamiento del conjunto de datos original (manteniendo el tamaño muestral).

Para aproximar la distribución en el muestreo por Monte Carlo, se genera un número grande \(B\) de réplicas bootstrap:

\(\mathbf{X}^{\ast (b)}=\left( X_1^{\ast (b)},\ldots ,X_n^{\ast (b)} \right)\) muestra bootstrap (remuestra), obtenida mediante muestreo con reemplazamiento de \(\mathbf{X}=\left( X_1,\ldots ,X_n \right)\).
\(\hat{\theta}^{\ast (b)} = T\left( \mathbf{X}^{\ast (b)} \right)\) valor del estadístico en la muestra bootstrap (réplica bootstrap del estadístico).

para \(b = 1,\ldots ,B\).

La idea original (bootstrap natural, Efron) es que la variabilidad de \(\hat{\theta}_{b}^{\ast }\) en torno a \(\hat{\theta}\) aproxima la variabilidad de \(\hat{\theta}\) en torno a \(\theta\): la distribución de \(\hat{\theta}_{b}^{\ast }-\hat{\theta}\) (en el universo bootstrap) aproxima la distribución de \(\hat{\theta}-\theta\) (en la población).

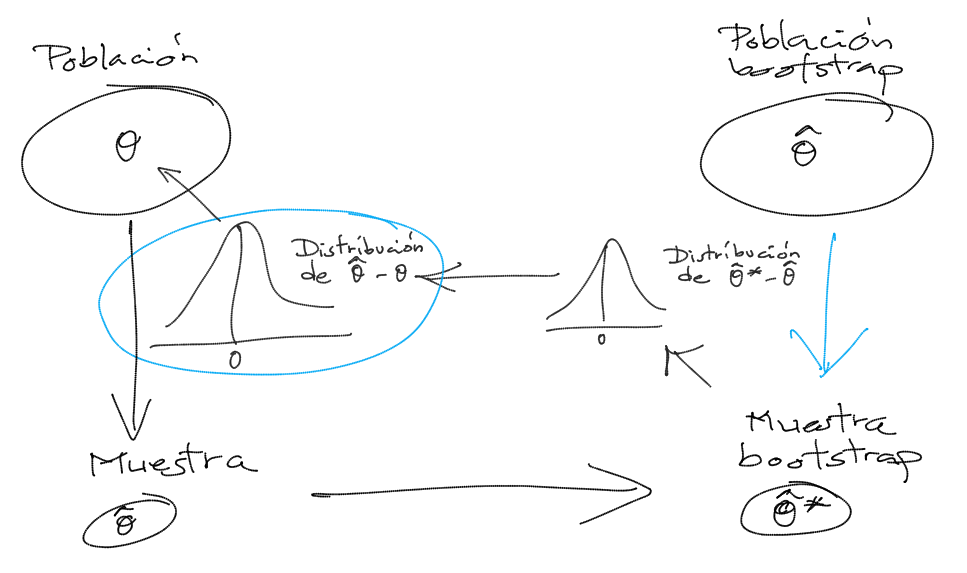
Figura 8.1: Esquema de la idea del boostrap (de Efron).

En general podríamos decir que la muestra es a la población lo que la muestra bootstrap es a la muestra.

Ejemplo 8.1 (aproximación bootstrap de la distribución de la media muestral)

Como ejemplo ilustrativo consideramos una muestra simulada de tamaño \(n=100\) de una normal estándar y la media muestral como estimador de la media teórica:

set.seed(1)
n <- 100
mean_teor <- 0
sd_teor <- 1  
muestra <- rnorm(n, mean = mean_teor, sd = sd_teor)

El valor del estadístico en la muestra es:

estadistico <- mean(muestra)

Representamos la distribución de la muestra:

hist(muestra, freq = FALSE, xlim = c(-3, 3),
     main = '', xlab = 'x', ylab = 'densidad')
abline(v = estadistico, lty = 2)
curve(dnorm, col = "blue", add = TRUE)
abline(v = mean_teor, col = "blue", lty = 2)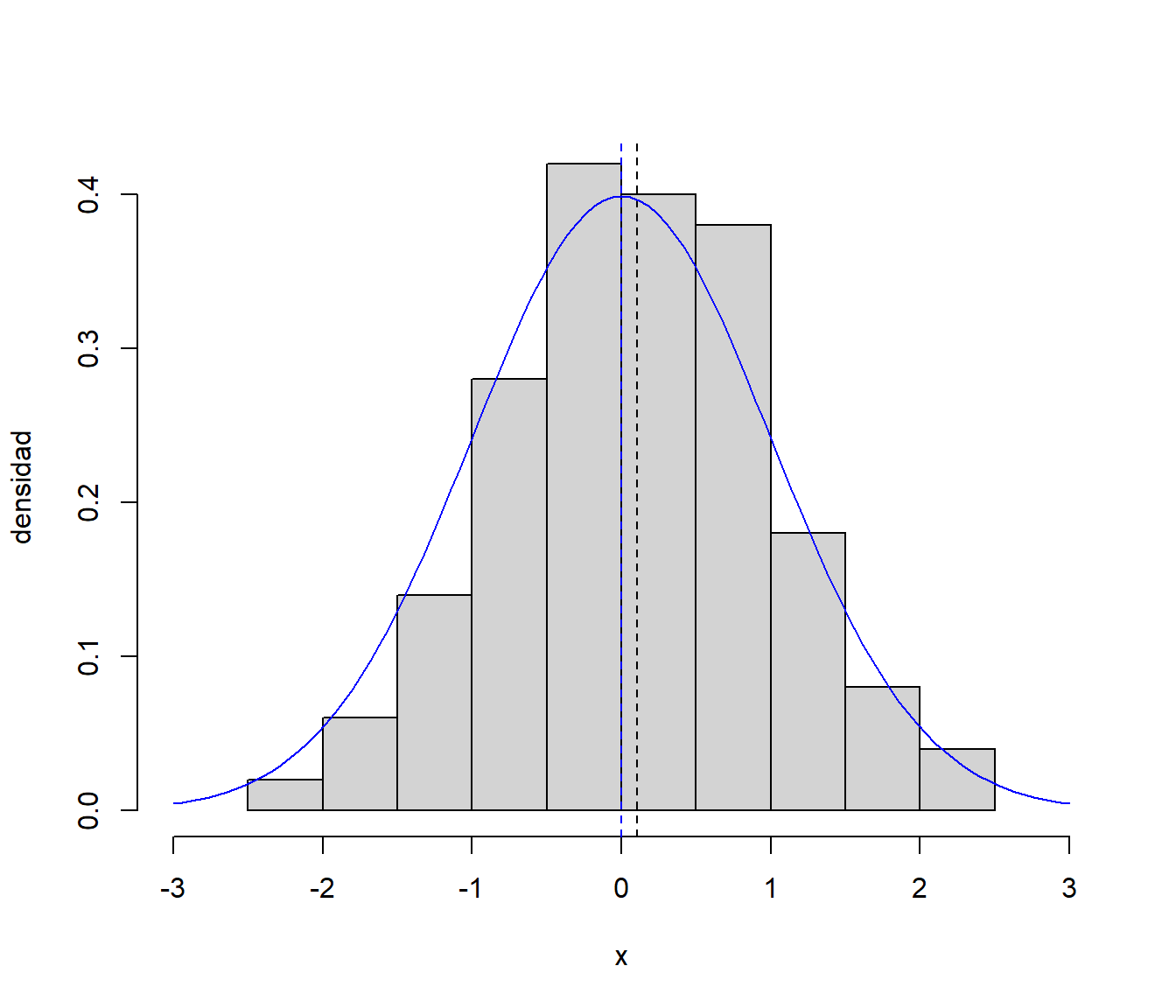

Figura 8.2: Distribución de la muestra simulada (y distribución teórica en azul).

Como aproximación de la distribución poblacional, desconocida en la práctica, siempre podemos considerar la distribución empírica (o una versión suavizada: bootstrap suavizado; Sección 9.3). Alternativamente podríamos asumir un modelo paramétrico y estimar los parámetros a partir de la muestra (bootstrap paramétrico; Sección 9.2.

# Distribución bootstrap uniforme
curve(ecdf(muestra)(x), xlim = c(-3, 3), ylab = "F(x)", type = "s")
# Distribución bootstrap paramétrico (asumiendo normalidad)
curve(pnorm(x, mean(muestra), sd(muestra)), lty = 2, add = TRUE)
# Distribución teórica
curve(pnorm, col = "blue", add = TRUE)
legend("bottomright", legend = c("Empírica", "Aprox. paramétrica", "Teórica"),
       lty = c(1, 2, 1), col = c("black","black", "blue"))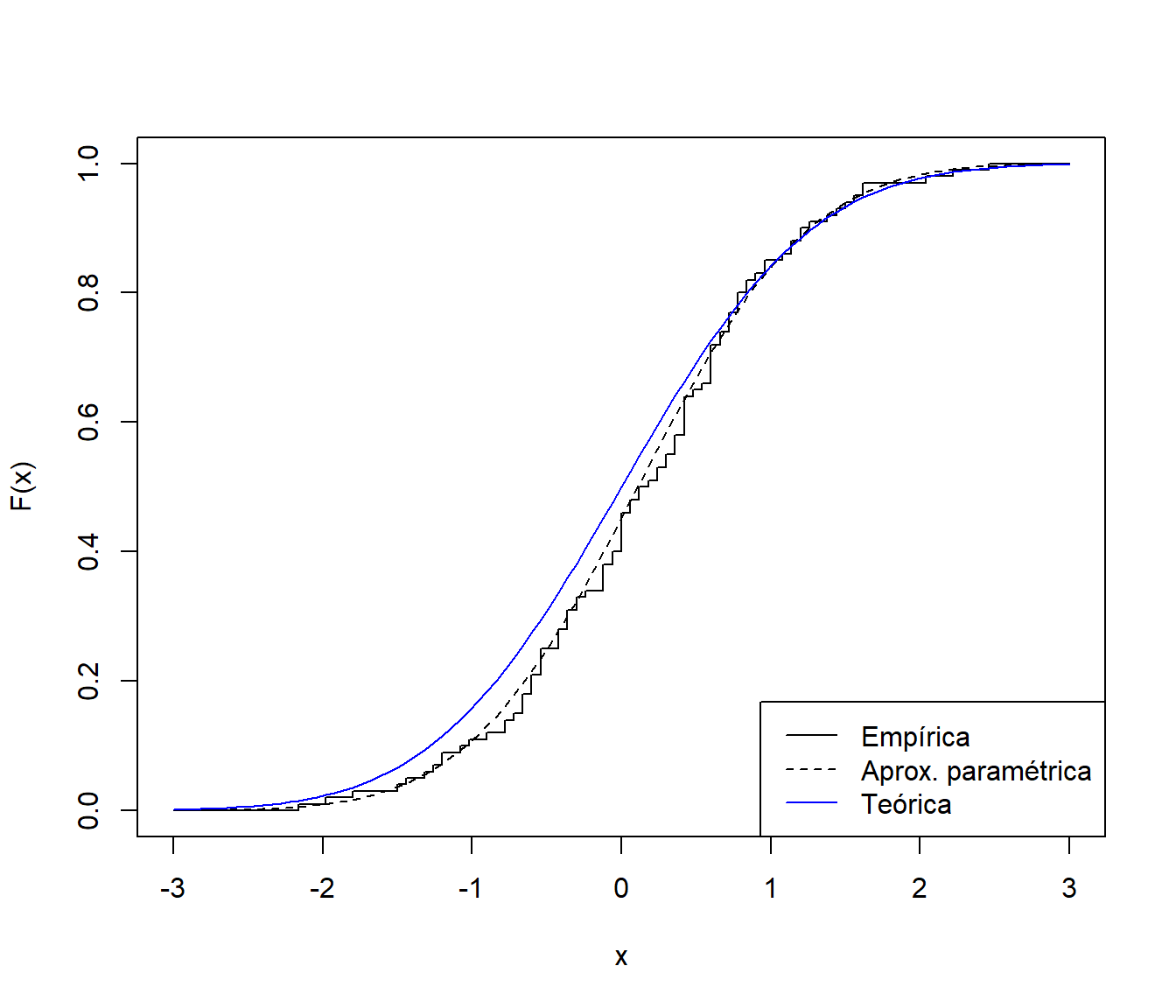

Figura 8.3: Distribución teórica de la muestra simulada y distintas aproximaciones.

En este caso (bootstrap uniforme) generamos las réplicas bootstrap empleando la distribución empírica:

set.seed(1)
B <- 1000
estadistico_boot <- numeric(B)
for (k in 1:B) {
    remuestra <- sample(muestra, n, replace = TRUE)
    estadistico_boot[k] <- mean(remuestra)
}

Podríamos emplear directamente las réplicas bootstrap del estimador para aproximar la distribución en el muestreo de la media muestral (esto es lo que se conoce como bootstrap percentil directo, o simplemente bootstrap percentil):

hist(estadistico_boot, freq = FALSE, xlim = c(-0.2, 0.5),
     ylab = "Densidad", main = "")
# Valor esperado bootstrap del estadístico
mean_boot <- mean(estadistico_boot)  
abline(v = mean_boot, lwd = 2)
# abline(v = estadistico, col = "blue")

# Distribución poblacional
curve(dnorm(x, mean_teor, sd_teor/sqrt(n)), col = "blue", add = TRUE)
abline(v = 0, col = "blue", lty = 2)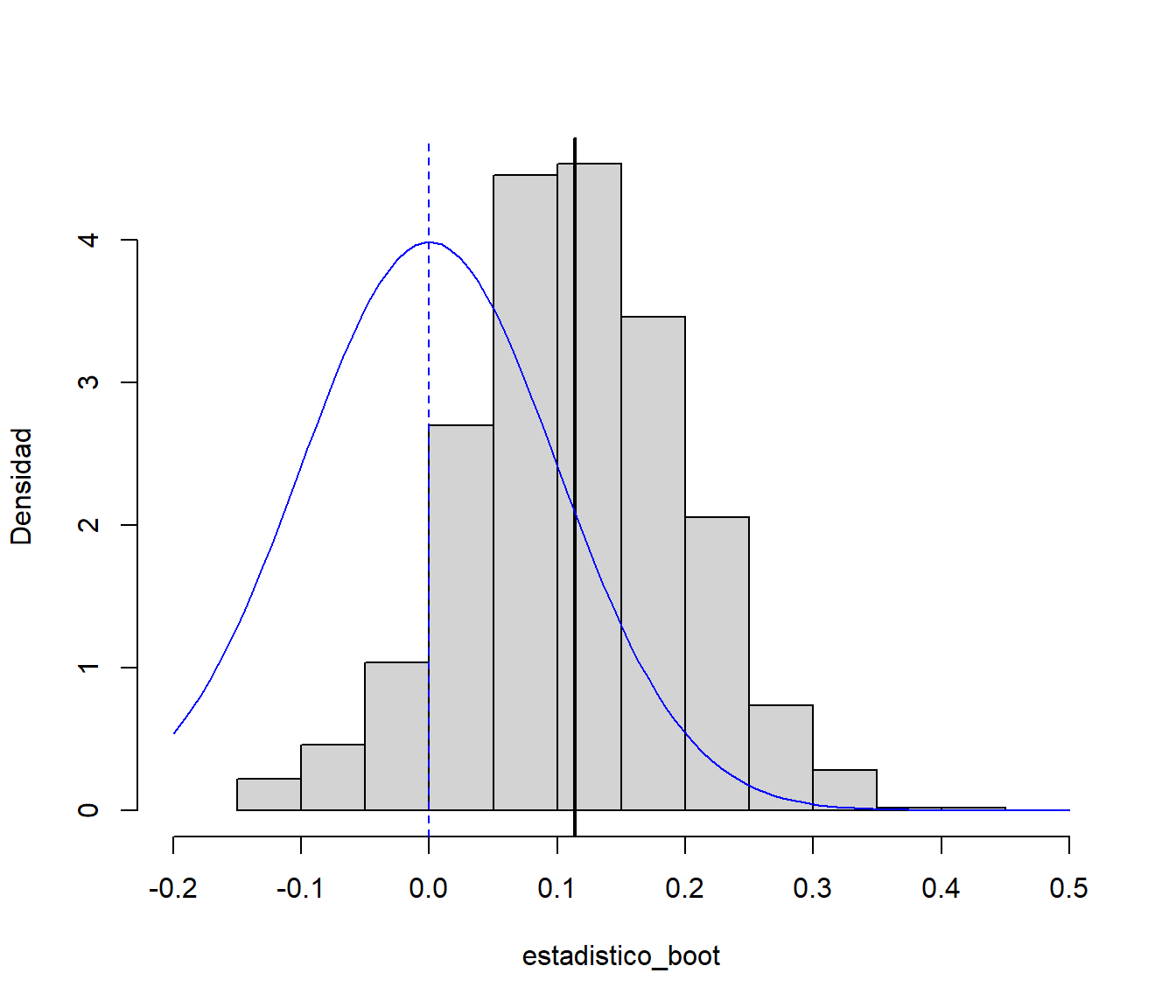

Figura 8.4: Aproximación de la distribución de la media muestral centrada mediante bootstrap percentil (uniforme).

Sin embargo, especialmente si el estimador es sesgado, puede ser preferible emplear la distribución de \(\hat{\theta}_{b}^{\ast }-\hat{\theta}\) como aproximación de la distribución de \(\hat{\theta}-\theta\) (bootstrap natural, básico o percentil básico):

hist(estadistico_boot - estadistico, freq = FALSE, 
     ylab = "Densidad", main = "")
# Distribución teórica
curve(dnorm(x, 0, sd_teor/sqrt(n)), col = "blue", add = TRUE)
abline(v = 0, col = "blue", lty = 2)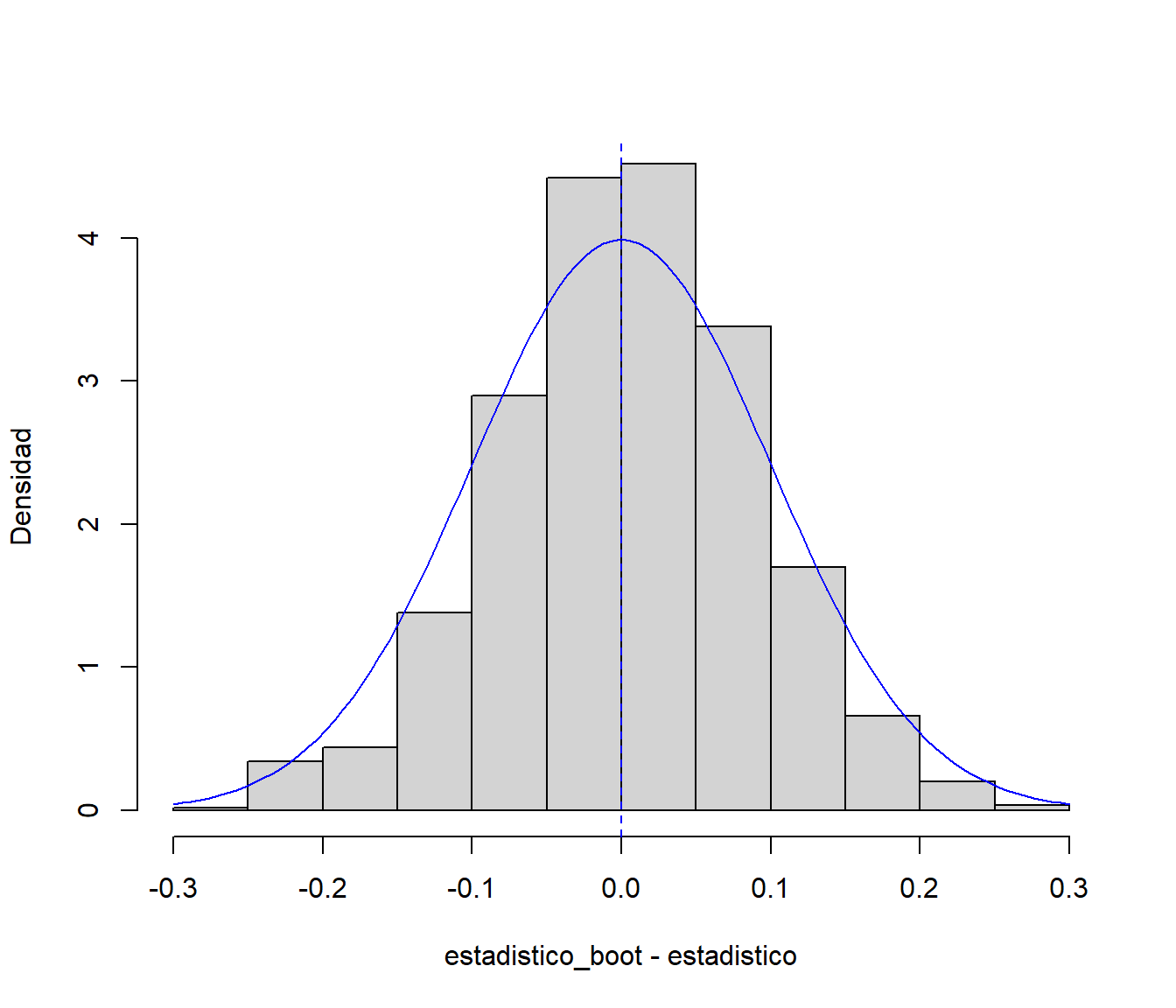

Figura 8.5: Aproximación de la distribución de la media muestral mediante bootstrap natural (uniforme).

Sin embargo, asintóticamente ambos procedimientos son equivalentes²⁶ y pueden dar lugar a los mismos resultados en determinados problemas de inferencia. Por ejemplo en la aproximación del sesgo y de la varianza de un estimador (Sección ??):

# Sesgo (teor=0)
mean_boot - estadistico # mean(estadistico_boot - estadistico)

## [1] 0.004714973

# Error estándar
sd(estadistico_boot) # sd(estadistico_boot - estadistico)

## [1] 0.08610306

# Error estándar teórico
sd_teor/sqrt(n)

## [1] 0.1

Por este motivo en algunas referencias más teóricas no se diferencia entre ambos métodos y se denominan simplemente bootstrap percentil.↩︎