6.6 Simulación basada en cópulas

Una cópula es una función de distribución multidimensional con distribuciones marginales uniformes (e.g. Nelsen, 2006; Hofert, 2018). Se emplean principalmente para la construcción de distribuciones multivariantes a partir de distribuciones marginales (también en análisis de dependencia y medidas de asociación). La idea es que la estructura de dependencia no depende de las distribuciones marginales.

Por simplicidad nos centraremos en el caso bidimensional. El teorema central en la teoría de cópulas es el teorema de Sklar (1959), que en este caso es:

Teorema 6.1 (de Sklar caso bidimensional)
Si \((X,Y)\) es una variable aleatoria bidimensional con función de distribución conjunta \(F(\cdot,\cdot)\) y distribuciones marginales \(F_1(\cdot)\) y \(F_2(\cdot)\) respectivamente, entonces existe una cópula \(C(\cdot,\cdot)\) tal que: \[F(x,y)=C\left( F_1(x),F_2(y)\right) ,\quad \forall x,y\in\mathbb{R}.\] Además, si \(F_1(\cdot)\) y \(F_2(\cdot)\) son continuas entonces \(C(\cdot,\cdot)\) es única. Siendo el recíproco también cierto.

6.6.1 Cópulas Arquimedianas

Además de las cópulas Gausianas, es una de las familias de cópulas más utilizadas. Son de la forma: \[C(x_1,x_2,\dots,x_d) =\Psi^{-1}\left( \sum_{i=1}^d\Psi\left( F_i(x_i)\right)\right),\] siendo \(\Psi\) su función generadora.

Una condición suficiente para que sea una cópula multidimensional válida es que \(\Psi(1)=0\), \(\lim \limits_{x\ \rightarrow0}\Psi(x)=\infty\), \(\Psi^{\prime}(x)<0\) y \(\Psi^{\prime \prime}(x)>0\).

Ejemplos:

Cópula producto o independiente: \(\Psi(x)=-\ln(x)\), \[F(x,y)=F_1(x)F_2(y).\]
Cópula de Clayton: \(\Psi(x)=\frac{1}{\alpha}\left( x^{-\alpha }-1\right) ;\alpha>0\), \[F(x,y)=(F_1(x)^{-\alpha}+F_2(y)^{-\alpha}-1)^{-1/\alpha}.\]
Cópula de Gumbel: \(\Psi(x)=\left( -\ln(x)\right)^{\alpha};\alpha \geq1\)

6.6.2 Simulación

Las cópulas pueden facilitar notablemente la simulación de la distribución conjunta. Si \((U,V)\sim C(\cdot,\cdot)\) (marginales uniformes): \[\left( F_1^{-1}(U),F_2^{-1}(V)\right) \sim F(\cdot,\cdot)\]

En la mayoría de los casos se dispone de expresiones explicitas de \(C_{u}(v)\equiv C_2\left( \left. v\right \vert u\right)\) y de su inversa \(C_{u}^{-1}(w)\), por lo que se puede generar \((U,V)\) fácilmente mediante el método secuencial de distribuciones condicionadas descrito en la Sección 6.4.

Algoritmo 6.5 (de simulación bidimensional mediante cópulas)

Generar \(U,W\sim \mathcal{U}(0,1)\)
Obtener \(V=C_{U}^{-1}(W)\)
Devolver \(\left( F_1^{-1}(U),F_2^{-1}(V)\right)\)

Ejemplo 6.9 (Cópula bidimensional de Clayton)

Consideramos una variable aleatoria bidimensional con distribuciones marginales uniformes y distribución bidimensional determinada por la cópula de Clayton.

Teniendo en cuenta que en este caso: \[C_{u}^{-1}(w)\equiv\left( u^{-\alpha}\left( w^{-\frac{\alpha}{\alpha+1}}-1\right) + 1 \right)^{-\frac{1}{\alpha}},\] la siguiente función permitiría generar una muestra de tamaño \(n\) de esta distribución:

rcclayton <- function(alpha, n) {
  val <- cbind(runif(n), runif(n))
  val[, 2] <- (val[, 1]^(-alpha) * 
              (val[, 2]^(-alpha/(alpha + 1)) - 1) + 1)^(-1/alpha)
  return(val)
}

Utilizando esta función generamos una muestra de tamaño 10000 y representamos gráficamente los valores obtenidos:

set.seed(54321)
rcunif <- rcclayton(2, 10000)
plot(rcunif, xlab = "u", ylab = "v")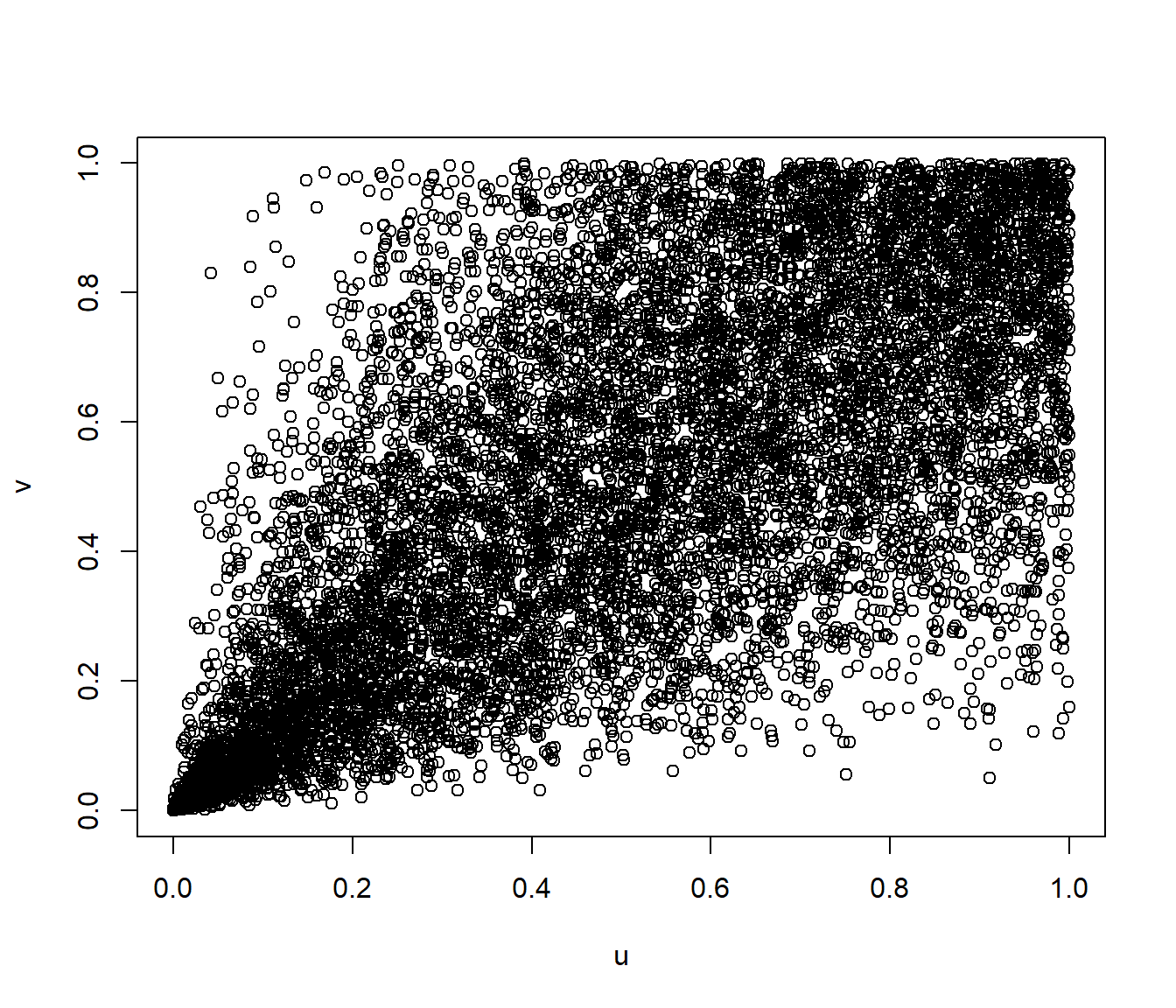

Figura 6.7: Gráfico de dispersión de los valores generados con distribución bidimensional de Clayton.

Podemos representar la densidad conjunta (con sm::sm.density()):

# if(!require(sm)) stop('Required package `sm` not installed.')
sm::sm.density(rcunif, xlab = "u", ylab = "v", zlab = "Density")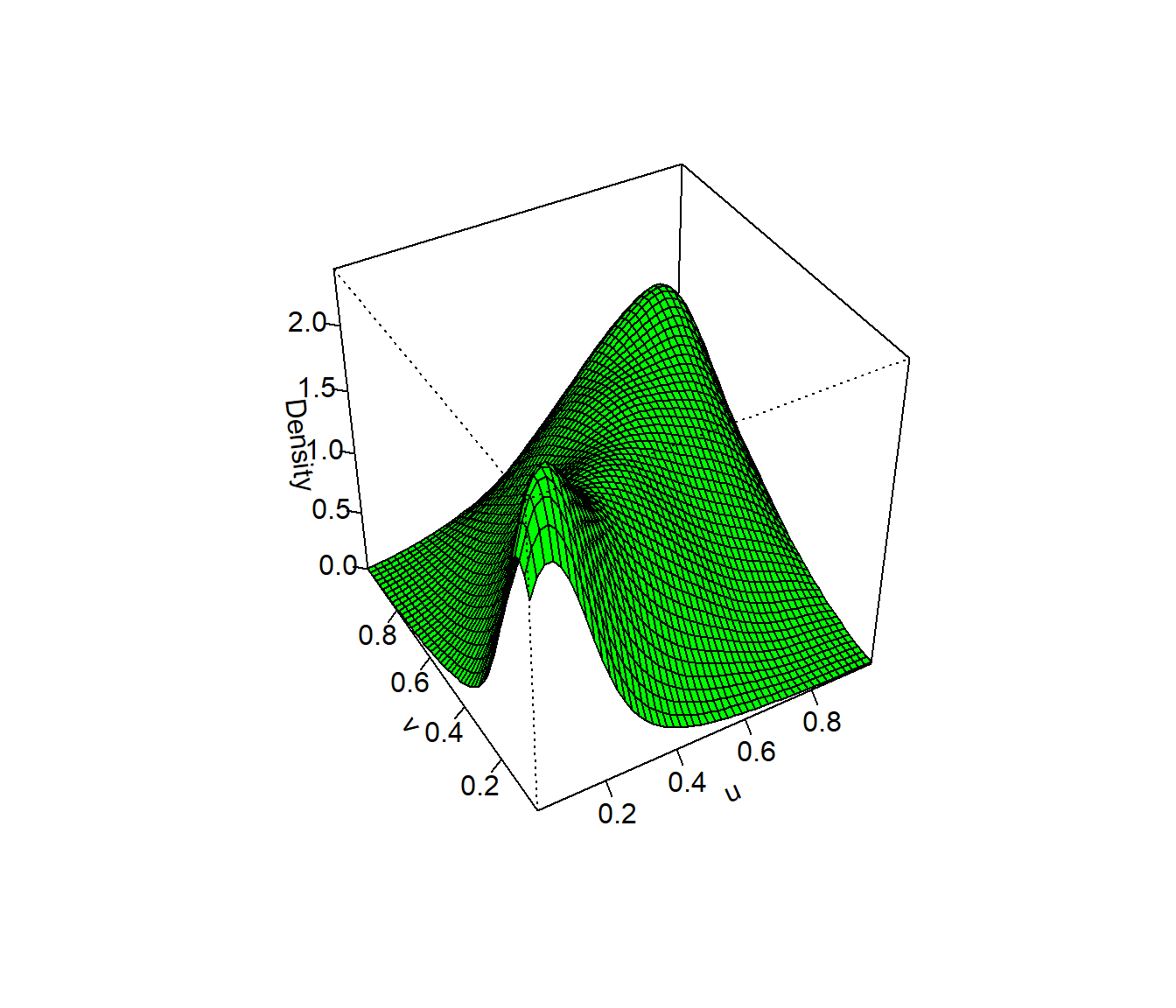

Figura 6.8: Densidad conjunta de los valores generados con distribución bidimensional de Clayton

y las distribuciones marginales:

par.old <- par(mfrow = c(1, 2))
hist(rcunif[,1], freq = FALSE, xlab = "u")
abline(h = 1)
hist(rcunif[,2], freq = FALSE, xlab = "v")
abline(h = 1)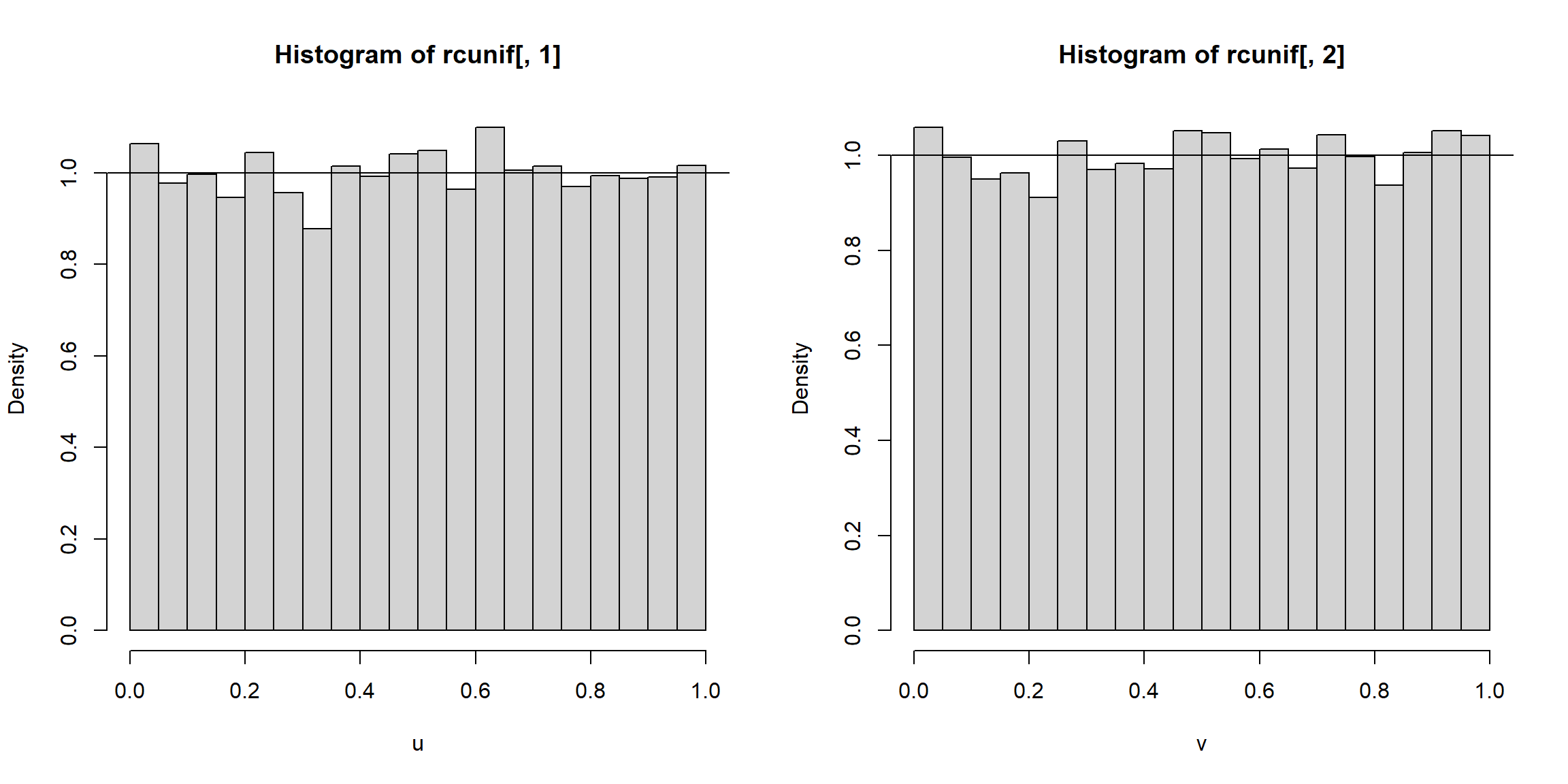

Figura 6.9: Distribuciones marginales de los valores generados con distribución bidimensional de Clayton.

par(par.old)

Empleando el paquete copula:

if(!require(copula)) stop('Required pakage `copula` not installed.')
clayton.cop <- claytonCopula(2, dim = 2) # caso bidimensional
y <- rCopula(10000, clayton.cop)
plot(y, xlab = "u", ylab = "v")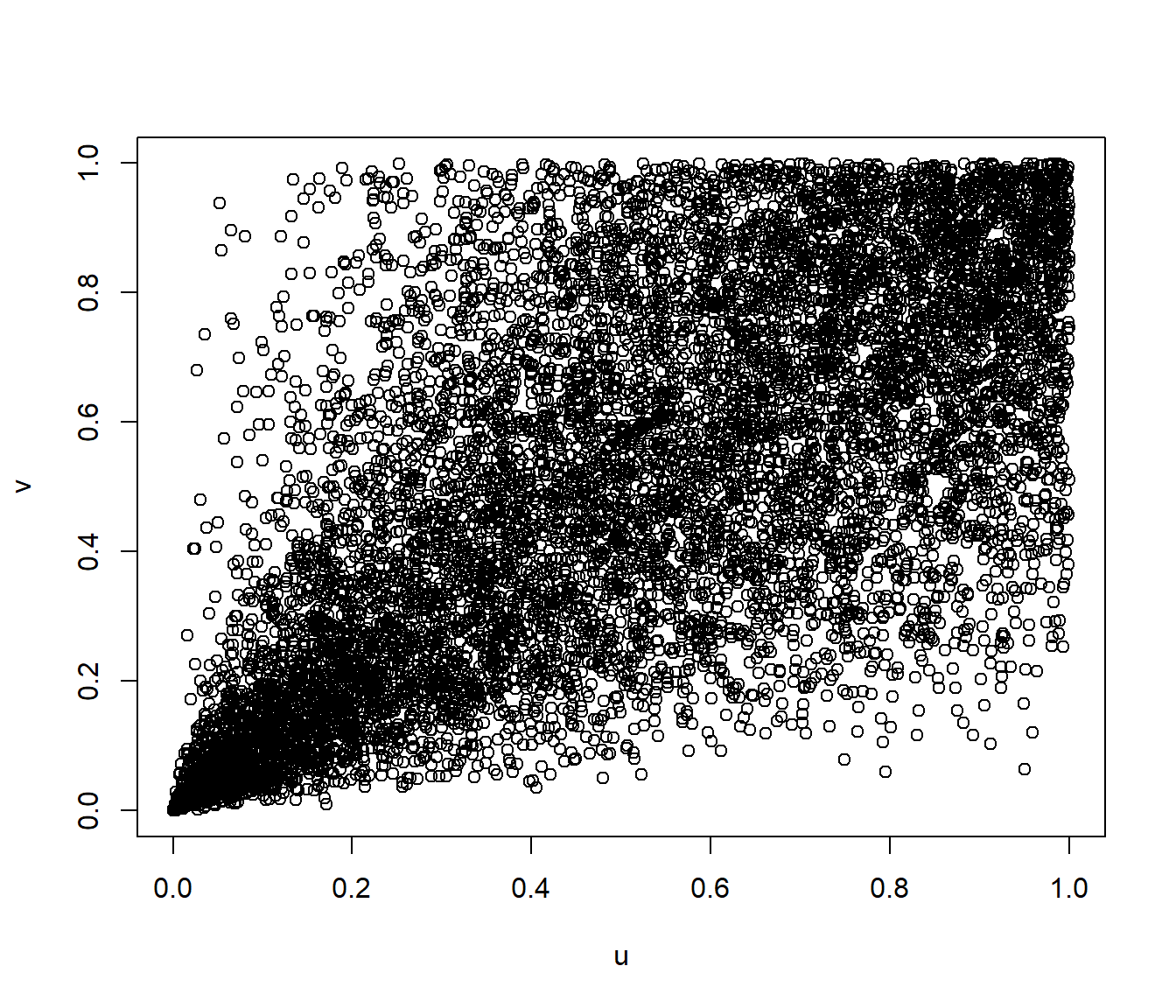

Figura 6.10: Gráfico de dispersión de los valores generados con distribución bidimensional de Clayton empleando el paquete copula.

clayton.cop <- claytonCopula(2, dim = 3) # caso tridimensional
y <- rCopula(10000, clayton.cop)
# scatterplot3d::scatterplot3d(y)
plot3D:::points3D(y[,1], y[,2], y[, 3], colvar = NULL, 
                  xlab = "u1", ylab = "u2", zlab = "u3")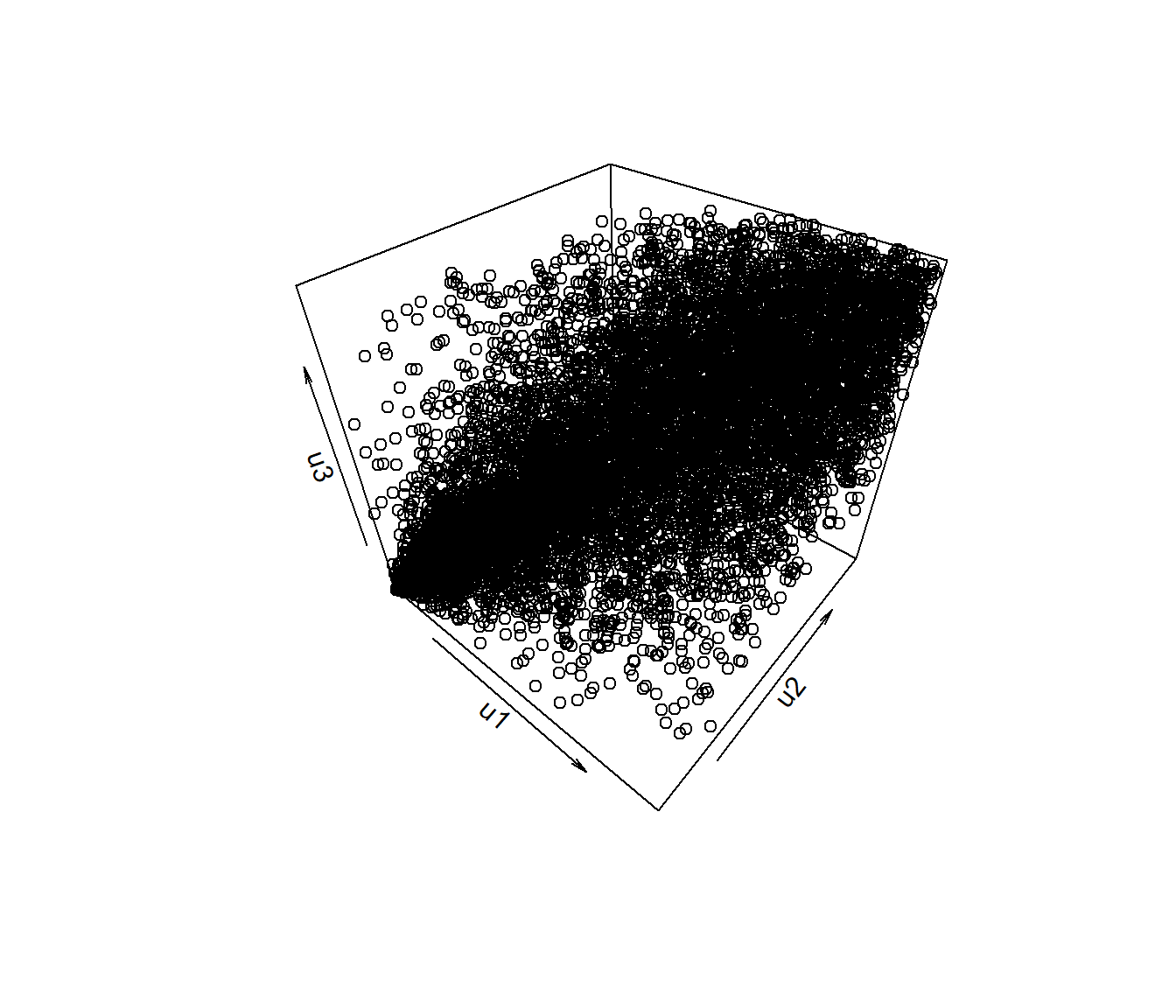

Figura 6.11: Gráfico de dispersión de los valores generados con distribución trididimensional de Clayton empleando el paquete copula.

Por ejemplo, podemos generar una muestra de una variable aleatoria bidimensional con distribuciones marginales exponenciales de parámetros 1 y 2, respectivamente (y distribución bidimensional determinada por la cópula de Clayton), transformando la muestra anterior:

rcexp <- cbind(qexp(rcunif[,1], 1), qexp(rcunif[,2], 2))
plot(rcexp, xlab = "exp1", ylab = "exp2")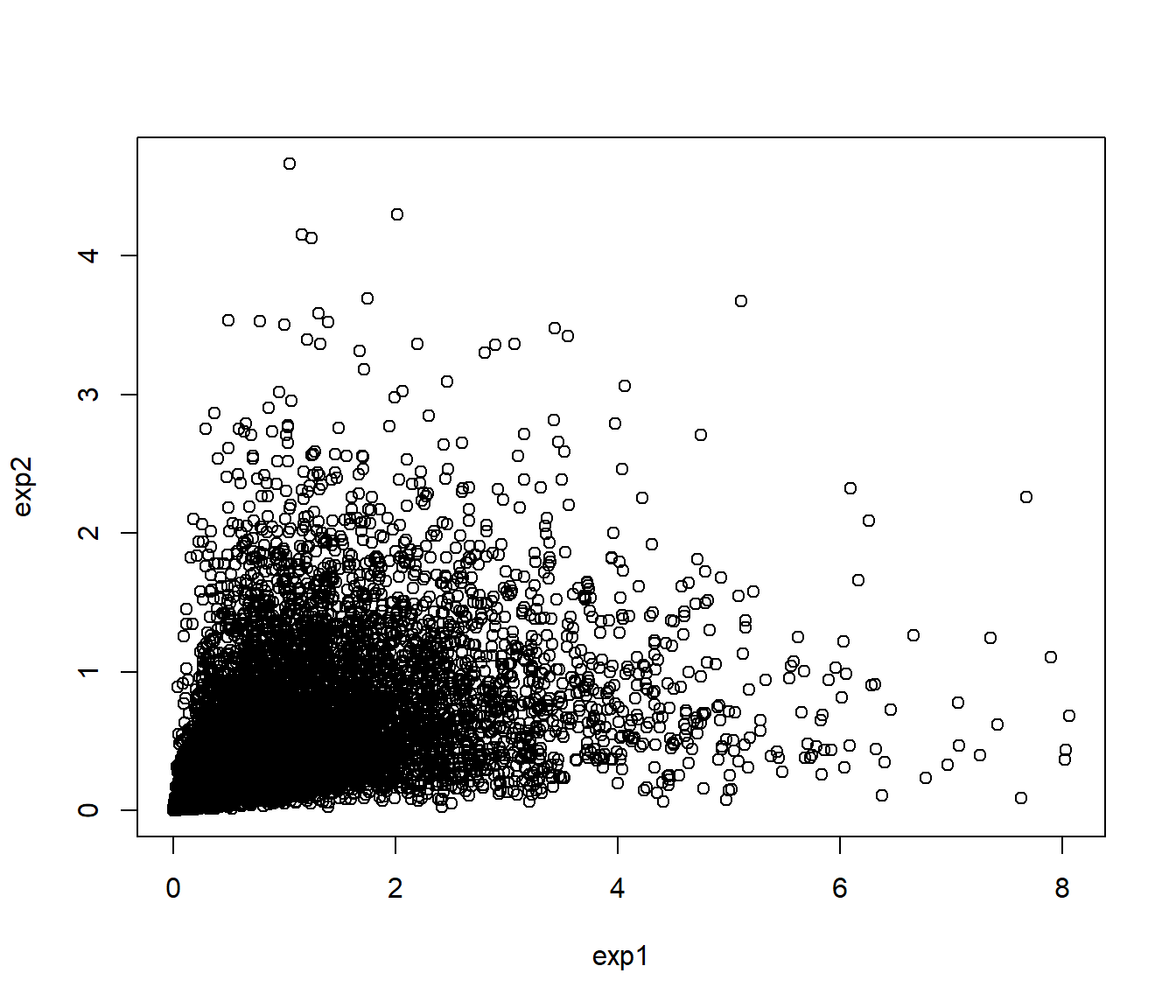

Figura 6.12: Gráfico de dispersión de los valores generados con distribución exponencial y dependencia definida por la cópula de Clayton.

# Distribuciones marginales
par.old <- par(mfrow = c(1, 2))
hist(rcexp[,1], freq = FALSE, xlab = "exp1")
curve(dexp(x, 1), add = TRUE)
hist(rcexp[,2], freq = FALSE, xlab = "exp2")
curve(dexp(x, 2), add = TRUE)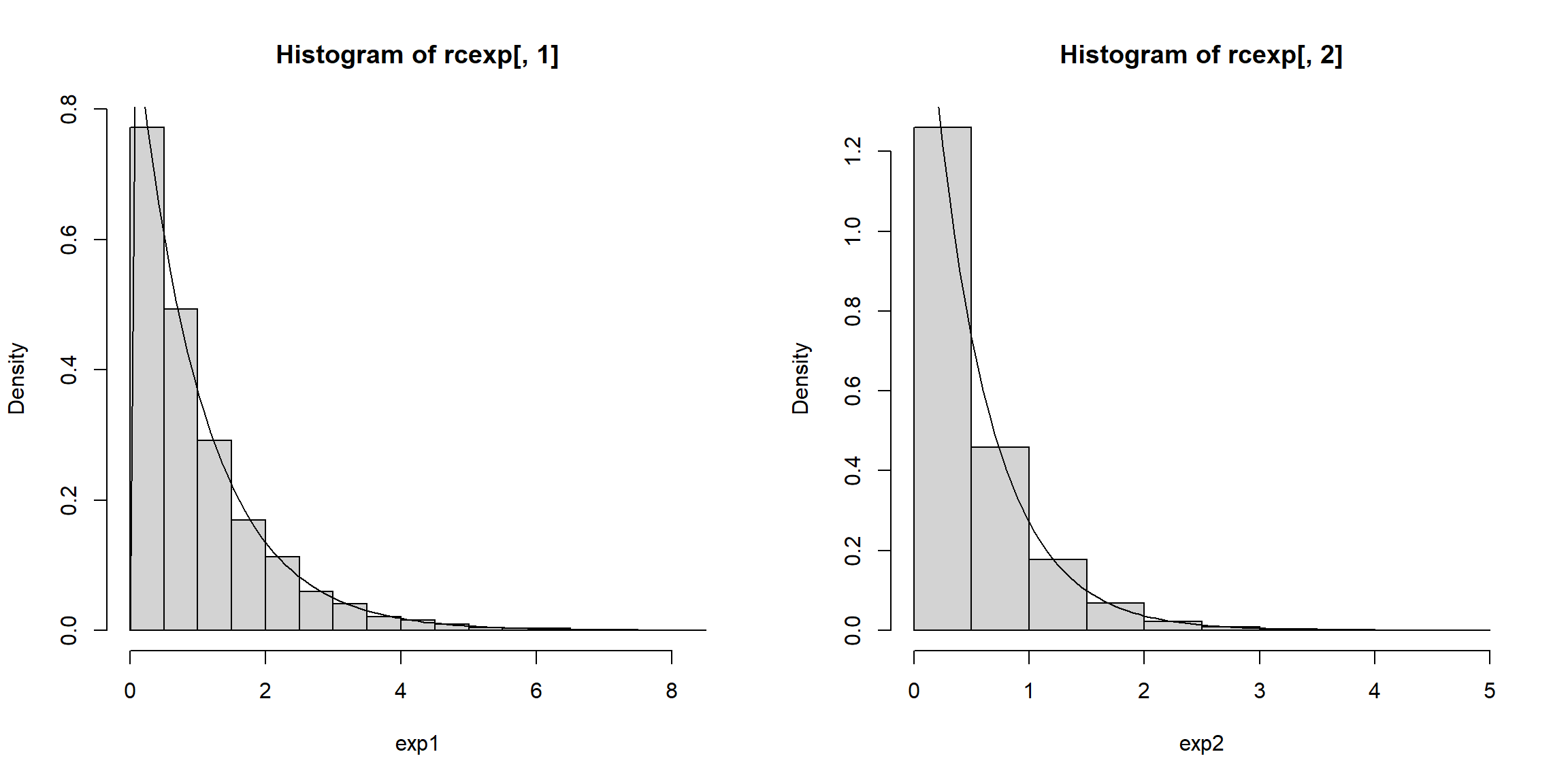

Figura 6.13: Distribuciones marginales exponenciales de los valores generados con dependencia definida por la cópula de Clayton.

par(par.old)