10.3 Contrastes de hipótesis bootstrap

El objetivo de los contrastes de hipótesis es, a partir de la información que proporciona una muestra, decidir (tratando de controlar el riesgo de equivocarse al no disponer de toda la información) entre dos hipótesis sobre alguna característica de interés de la población: hipótesis nula ($H_{0}$) e hipótesis alternativa ($H_{1}$).

Entre los distintos tipos de contrastes de hipótesis (e.g. paramétricos, no paramétricos, …), nos centraremos principalmente en los contrastes de bondad de ajuste. En este caso interesará distinguir principalmente entre hipótesis nulas simples (especifican un único modelo) y compuestas (especifican un conjunto/familia de modelos).

Para realizar el contraste se emplea un estadístico $D\left( X_1,\ldots ,X_n;H_0\right)$, que mide la discrepancia entre la muestra observada y la hipótesis nula, con distribución conocida (o que se puede aproximar) bajo $H_0$. Por ejemplo, en el caso de una hipótesis nula paramétrica es habitual emplear un estadístico studentizado de la forma: \[D\left( X_1,\ldots ,X_n;H_0\right) = \frac{\hat{\theta}-\theta _0}{\hat\sigma_{\hat\theta}}\] (o algún tipo de razón de verosimilitudes).

La regla de decisión depende de la hipótesis alternativa y del riesgo asumible al rechazar $H_0$ siendo cierta: \[P\left( \text{rechazar }H_0\mid H_0\text{ cierta}\right) =\alpha,\] denominado nivel de significación. Se determina una región de rechazo (RR) a partir de los valores que tiende a tomar el estadístico cuando $H_1$ es cierta, de forma que³²: \[P\left( D\in RR \mid H_0\text{ cierta}\right) =\alpha.\] Se rechaza la hipótesis nula cuando el valor observado del estadístico $\hat{d}=D\left( x_1,\ldots ,x_n;H_0\right)$ pertenece a la región de rechazo.

Para medir el nivel de evidencia en contra de $H_0$ se emplea el $p$-valor del contraste (también denominado valor crítico o tamaño del contraste), el menor valor del nivel de significación para el que se rechaza $H_0$ (que se puede interpretar también como la probabilidad de obtener una discrepancia mayor o igual que $\hat{d}$ cuando $H_0$ es cierta).

El cálculo del $p$-valor dependerá por tanto de la hipótesis altervativa. Por ejemplo, si el estadístico del contraste tiende a tomar valores grandes cuando $H_0$ es falsa (contraste unilateral derecho): \[p = P\left( D \geq \hat{d} \middle| H_0\right).\] En otros casos (contrastes bilaterales) hay evidencias en contra de $H_0$ si el estadístico toma valores significativamente grandes o pequeños. En estos casos la distribución del estadístico del contraste bajo $H_0$ suele ser simétrica en torno al cero, por lo que: \[p = 2P\left( D \geq \vert \hat{d} \vert \middle| H_0 \right).\] Pero si esta distribución es asimétrica: \[p = 2 \min \left\{ P\left( D \leq \hat{d} \middle| H_0 \right), P\left( D \geq \hat{d} \middle| H_0\right) \right\}.\]

La regla de decisión a partir del $p$-valor es siempre la misma. Rechazamos $H_0$, al nivel de significación $\alpha$, si $p \leq \alpha$, en cuyo caso se dice que el contraste es estadísticamente significativo (rechazamos $H_0$ con mayor seguridad cuanto más pequeño es el $p$-valor). Por tanto, la correspondiente variable aleatoria $\mathcal{P}$ debería verificar: \[P\left( \mathcal{P} \leq \alpha \middle| H_0\right)= \alpha.\] Es decir, la distribución del $p$-valor bajo $H_0$ debería ser $\mathcal{U}(0,1)$ (si la distribución del estadístico del constrate es continua).

En los métodos tradicionales de contrastes de hipótesis se conoce o se puede aproximar la distribución del estadístico del contraste bajo $H_0$. Muchas de estas aproximaciones están basadas en resultados asintóticos y pueden no ser adecuadas para tamaños muestrales pequeños. En ese caso, o si no se dispone de estas herramientas, se puede recurrir a métodos de remuestreo para aproximar el $p$-valor. Uno de los procedimientos más antiguos es el denominado contraste de permutaciones (Fisher, 1935; Pitman, 1937; Welch, 1937). Aunque el bootstrap paramétrico y el semiparamétrico son los procedimientos de remuestreo más empleados para aproximar la distribución del estadístico de contraste bajo la hipótesis nula.

La idea es obtener remuestras de una aproximación de la distribución del estadístico bajo $H_0$. En el bootstrap paramétrico y semiparamétrico se estima la distribución de los datos bajo la hipótesis nula, $\hat{F}_0$, y se obtienen réplicas del estadístico a partir de remuestras de esta distribución (no sería adecuado emplear directamente la distribución empírica). En el caso de los contrastes de permutaciones las remuestras se obtienen directamente de los datos, remuestreando sin reemplazamiento los valores de la respuesta (y manteniendo fijas las covariables).

Finalmente, se emplean las réplicas bootstrap del estadístico $d_1^{\ast},\ldots, d_B^{\ast}$ para aproximar el $p$-valor. Por ejemplo, en el caso de un contraste unilateral en el que el estadístico del contraste tiende a tomar valores grandes si la hipótesis nula es falsa, se podría emplear como aproximación: \[p_{boot} = \frac{1}{B}\#\left\{ d_i^{\ast} \geq \hat{d} \right\}.\] Mientras que en el caso bilateral, asumiendo que la distribución del estadístico no es necesariamente simétrica, habría que emplear: \[p_{boot} = \frac{2}{B} \min \left(\#\left\{ d_i^{\ast} \leq \hat{d} \right\}, \#\left\{ d_i^{\ast} \geq \hat{d} \right\}\right).\]

10.3.1 Contrastes bootstrap paramétricos

En los casos en los que la hipótesis nula especifica por completo la distribución (hipótesis nula simple) o solo desconocemos los valores de algunos parámetros (hipótesis nula paramétrica compuesta) podemos emplear bootstrap paramétrico para obtener las remuestras bootstrap de los datos (realmente en el primer caso se trataría de simulaciones Monte Carlo). Siempre hay que tener en cuenta que las réplicas bootstrap del estadístico se deberían obtener empleando el mismo procedimiento utilizado en la muestra (p.e. reestimando los parámetros si es el caso).

Ejemplo 10.3 (Contraste de Kolmogorov-Smirnov)

Se trata de un contraste de bondad de ajuste (similar a la prueba de Cramer-von Mises o a la de Anderson-Darling, implementadas en el paquete goftest de R, que son en principio mejores). A partir de $X_1,\ldots ,X_n$ m.a.s. de $X$ con función de distribución $F$, se pretende contrastar: \[\left \{ \begin{array}{l} H_0 : F = F_0 \\ H_1 : F \neq F_0 \end{array} \right. \] siendo $F_0$ una función de distribución continua. El estadístico empleado para ello compara la función de distribución bajo $H_0$ ($F_0$) con la empírica ($F_n$): \[\begin{aligned} D_n=&\sup_{x}|F_n(x)-F_0(x)| \\ =&\max_{1 \leq i\leq n}\left \{ |F_n(X_{(i)})-F_0(X_{(i)})|,|F_n(X_{(i-1)})-F_0(X_{(i)})|\right \} \\ =&\max_{1 \leq i\leq n}\left \{ \frac{i}{n}-F_0(X_{(i)}), \ F_0(X_{(i)})-\frac{i-1}{n}\right \} \\ =&\max_{1 \leq i\leq n}\left \{ D_{n,i}^{+},\ D_{n,i}^{-}\right \}, \end{aligned}\] y su distribución bajo $H_0$ no depende $F_0$ (es de distribución libre), si $H_0$ es simple y $F_0$ es continua. Esta distribución está tabulada (para tamaños muestrales grandes se utiliza la aproximación asintótica) y se rechaza $H_0$ si el valor observado $d$ del estadístico es significativamente grande: \[p = P \left( D_n \geq d \right) \leq \alpha.\] Este método está implementado en la función ks.test() del paquete base de R:

ks.test(x, y, ...)

donde x es un vector que contiene los datos, y es una función de distribución (o una cadena de texto que la especifica; también puede ser otro vector de datos para el contraste de dos muestras) y ... representa los parámetros de la distribución.

Si $H_0$ es compuesta, el procedimiento habitual es estimar los parámetros desconocidos por máxima verosimilitud y emplear $\hat{F}_0$ en lugar de $F_0$. Sin embargo, al proceder de esta forma es de esperar que $\hat{F}_0$ se aproxime más que $F_0$ a la distribución empírica, por lo que los cuantiles de la distribución de $D_n$ pueden ser demasiado conservativos (los $p$-valores tenderán a ser mayores de lo que deberían) y se tenderá a aceptar la hipótesis nula.

Para evitar este problema, en el caso de contrastar normalidad se desarrolló el test de Lilliefors, implementado en la función lillie.test() del paquete nortest (también hay versiones en este paquete para los métodos de Cramer-von Mises y Anderson-Darling). Como ejemplo analizaremos el comportamiento de ambos métodos para contrastar normalidad considerando 1000 pruebas con muestras de tamaño 30 de una $\mathcal{N}(0,1)$ (estudiaremos el tamaño de los contrastes).

# Valores iniciales
library(nortest)
set.seed(1)
nx <- 30
mx <- 0
sx <- 1
nsim <- 1000
# Realizar contrastes
pvalor.ks <- numeric(nsim)
pvalor.lil <- numeric(nsim)
for(isim in 1:nsim) {
  rx <- rnorm(nx, mx, sx)
  pvalor.ks[isim] <- ks.test(rx, "pnorm", mean(rx), sd(rx))$p.value
  pvalor.lil[isim] <- lillie.test(rx)$p.value
}

Bajo la hipótesis nula el $p$-valor debería de seguir una distribución uniforme, por lo que podríamos generar el correspondiente histograma para estudiar el tamaño del contraste. Alternativamente podríamos representar su función de distribución empírica, que se correspondería con la proporción de rechazos para los distintos niveles de significación.

old.par <- par(mfrow=c(2, 2))
# Test de KS
  # Histograma
hist(pvalor.ks, freq=FALSE, main = "")
abline(h=1, lty=2)   # curve(dunif(x,0,1), add=TRUE)
  # Distribución empírica
curve(ecdf(pvalor.ks)(x), type = "s", lwd = 2, main = '', 
      ylab = 'Proporción de rechazos', xlab = 'Nivel de significación')
abline(a=0, b=1, lty=2)   # curve(punif(x, 0, 1), add = TRUE)
# Test de Lilliefors
  # Histograma
hist(pvalor.lil, freq=FALSE, main = "")
abline(h=1, lty=2)   # curve(dunif(x,0,1), add=TRUE)
  # Distribución empírica
curve(ecdf(pvalor.lil)(x), type = "s", lwd = 2, main = '', 
      ylab = 'Proporción de rechazos',  xlab = 'Nivel de significación')
abline(a=0, b=1, lty=2)   # curve(punif(x, 0, 1), add = TRUE)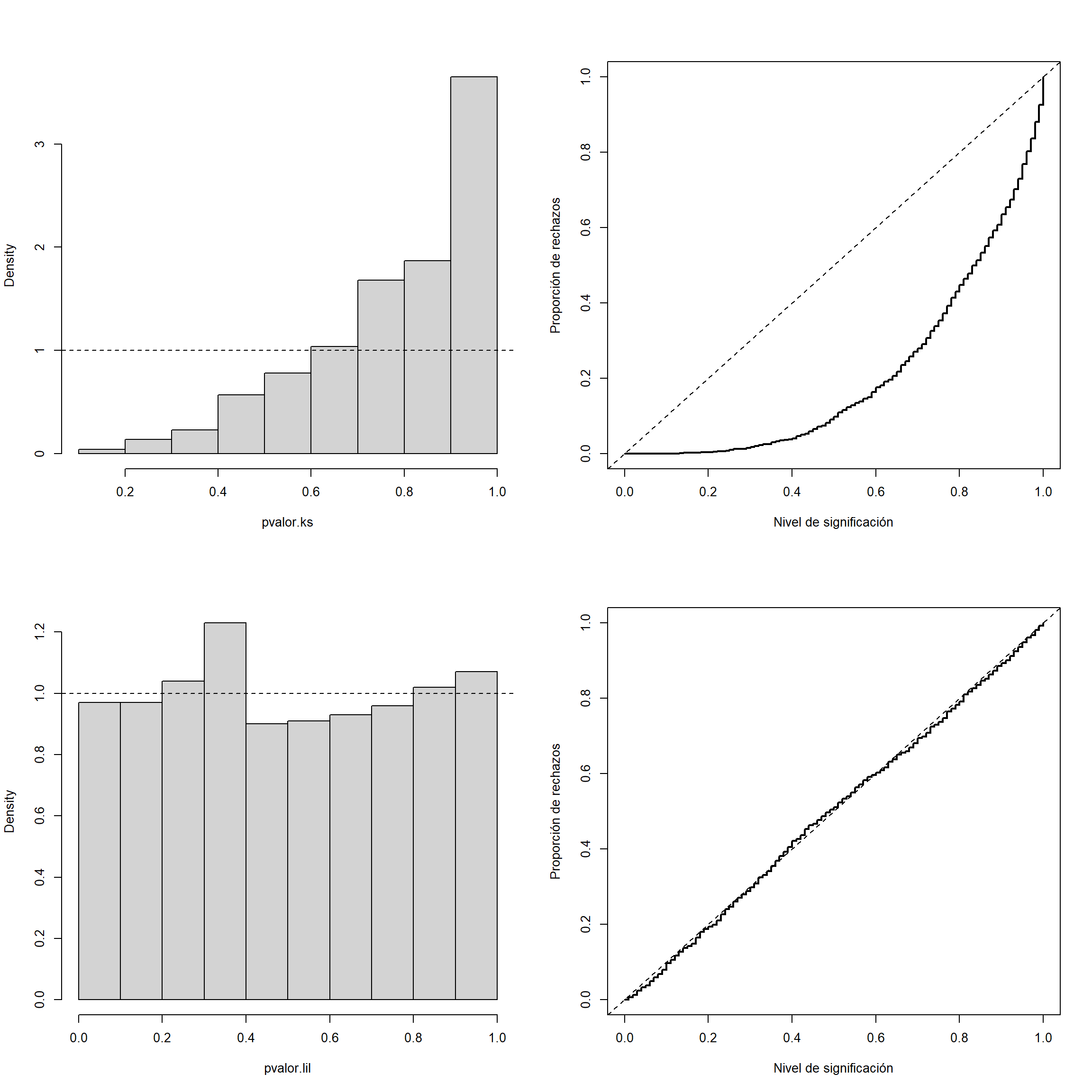

Distribución del p-valor (izquierda) y tamaño (proporción de rechazos bajo la hipótesis nula; derecha), aproximados por Monte Carlo, para el contraste de Kolmogorov-Smirnov (arriba) y el de Lilliefors (abajo).

Figura 10.2: Distribución del p-valor (izquierda) y tamaño (proporción de rechazos bajo la hipótesis nula; derecha), aproximados por Monte Carlo, para el contraste de Kolmogorov-Smirnov (arriba) y el de Lilliefors (abajo).

par(old.par)

En el caso del contraste de Kolmogorov-Smirnov (KS) se observa que el $p$-valor tiende a tomar valores grandes y por tanto se rechaza la hipótesis nula muchas menos veces de las que se debería.

En el caso de otras distribuciones se puede emplear bootstrap paramétrico para aproximar la distribución del estadístico del contraste. Es importante recordar que el bootstrap debería imitar el procedimiento empleado sobre la muestra, por lo que en este caso también habría que estimar los parámetros en cada remuestra (en caso contrario aproximaríamos la distribución de $D_n$).

Por ejemplo, la siguiente función implementaría el contraste KS de bondad de ajuste de una variable exponencial aproximando el $p$-valor mediante bootstrap paramétrico:

ks.exp.boot <- function(x, nboot = 10^3) {
  DNAME <- deparse(substitute(x))
  METHOD <- "Kolmogorov-Smirnov Test of pexp by bootstrap" 
  n <- length(x)
  RATE <- 1/mean(x)
  ks.exp.stat <- function(x, rate = 1/mean(x)) { # se estima el parámetro
    DMinus <- pexp(sort(x), rate=rate) - (0:(n - 1))/n
    DPlus <- 1/n - DMinus
    Dn = max(c(DMinus, DPlus))
  }  
  STATISTIC <- ks.exp.stat(x, rate = RATE) 
  names(STATISTIC) <- "Dn"
  # PVAL <- 0
  # for(i in 1:nboot) {
  #   rx <- rexp(n, rate = RATE)
  #   if (STATISTIC <= ks.exp.stat(rx)) PVAL <- PVAL + 1
  # }
  # PVAL <- PVAL/nboot
  # PVAL <- (PVAL + 1)/(nboot + 1) # Alternativa para aproximar el p-valor
  rx <- matrix(rexp(n*nboot, rate = RATE), ncol=n)
  PVAL <- mean(STATISTIC <= apply(rx, 1, ks.exp.stat))
  return(structure(list(statistic = STATISTIC, alternative = "two.sided", 
                   p.value = PVAL, method = METHOD, data.name = DNAME), 
                   class = "htest"))
}

Como ejemplo estudiaremos el caso de contrastar una distribución exponencial considerando 500 pruebas con muestras de tamaño 30 de una $Exp(1)$ y 200 réplicas bootstrap (para disminuir el tiempo de computación).

# Valores iniciales
set.seed(1)
nx <- 30
ratex <- 1
nsim <- 500
# Realizar contrastes
pvalor.ks <- numeric(nsim)
pvalor.ks.boot <- numeric(nsim)
for(isim in 1:nsim) {
  rx <- rexp(nx, ratex)
  pvalor.ks[isim] <- ks.test(rx, "pexp", 1/mean(rx))$p.value
  pvalor.ks.boot[isim] <- ks.exp.boot(rx, nboot = 200)$p.value
}
# Generar gráficos
old.par <- par(mfrow=c(2, 2))
# Test de KS
  # Histograma
hist(pvalor.ks, freq=FALSE, main = "")
abline(h=1, lty=2)   # curve(dunif(x,0,1), add=TRUE)
  # Distribución empírica
curve(ecdf(pvalor.ks)(x), type = "s", lwd = 2, main = '', 
      ylab = 'Proporción de rechazos', xlab = 'Nivel de significación')
abline(a=0, b=1, lty=2)   # curve(punif(x, 0, 1), add = TRUE)
# Contraste bootstrap paramétrico
  # Histograma
hist(pvalor.ks.boot, freq=FALSE, main = "")
abline(h=1, lty=2)   # curve(dunif(x,0,1), add=TRUE)
  # Distribución empírica
curve(ecdf(pvalor.ks.boot)(x), type = "s", lwd = 2, main = '', 
      ylab = 'Proporción de rechazos',  xlab = 'Nivel de significación')
abline(a=0, b=1, lty=2)   # curve(punif(x, 0, 1), add = TRUE)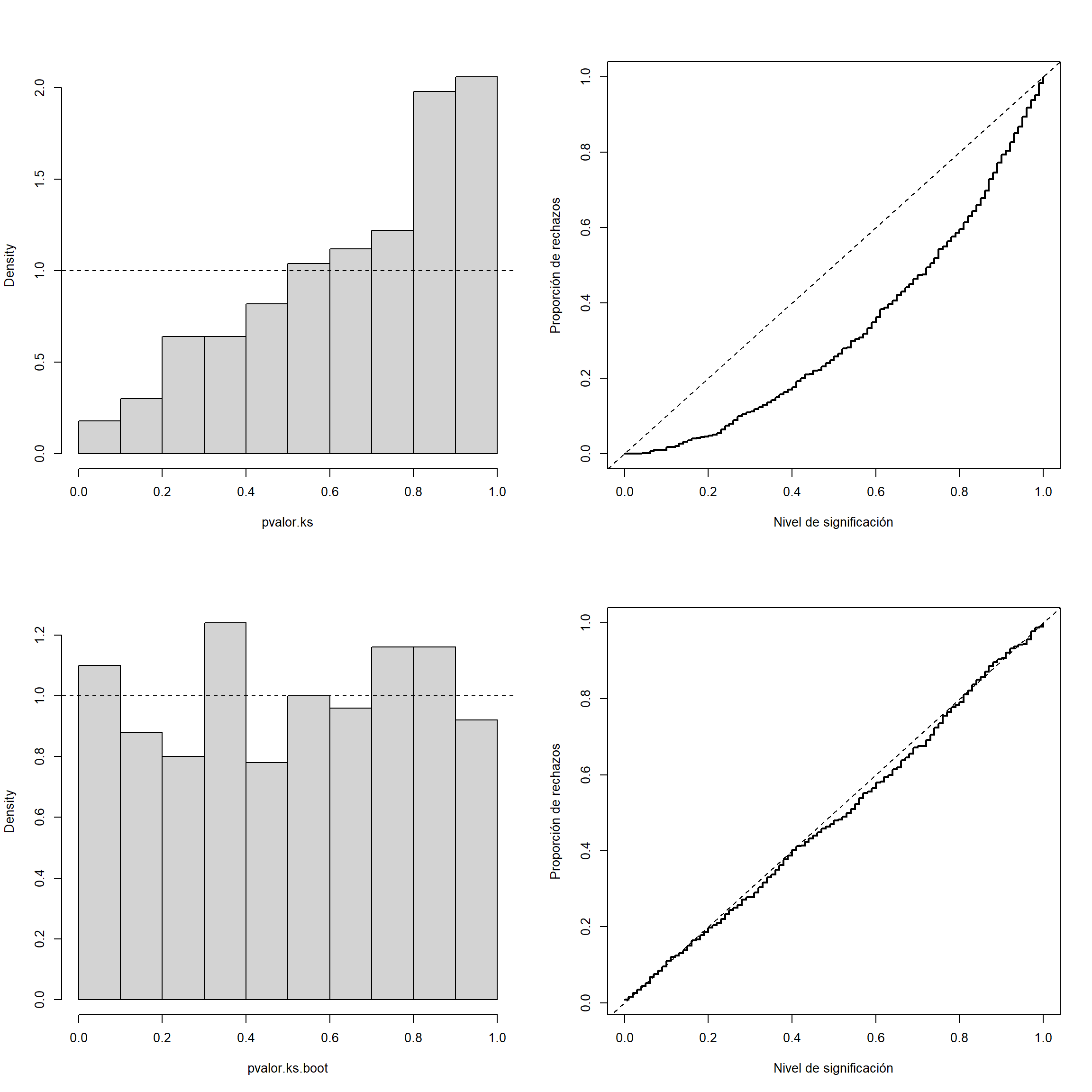

Figura 10.3: Distribución del p-valor (izquierda) y tamaño (proporción de rechazos bajo la hipótesis nula; derecha), aproximados por Monte Carlo, para el contraste de Kolmogorov-Smirnov (arriba) y el correspondiente contraste boostrap paramétrico (abajo).

par(old.par)

El estadístico de Kolmogorov-Smirnov Dn = max(c(DMinus, DPlus)) tiene ventajas desde el punto de vista teórico, pero puede no ser muy potente para detectar diferencias entre la distribución bajo la hipótesis nula y la distribución de los datos. La ventaja de la aproximación por simulación es que no estamos atados a resultados teóricos y podemos emplear el estadístico que se considere oportuno (la principal desventaja es el tiempo de computación). Por ejemplo, podríamos pensar en utilizar como estadístico la suma de los errores en valor absoluto del correspondiente gráfico PP, y solo habría que cambiar el estadístico Dn en la función ks.exp.sim por Dn = sum(abs( (1:n - 0.5)/n - pexp(sort(x), rate=rate) )).

10.3.2 Contrastes de permutaciones

Supongamos que a partir de una muestra $\left\{ \left( \mathbf{X}_i, Y_i\right): i=1,\ldots, n \right\}$ estamos interesados en contrastar la hipótesis nula de independencia entre $\mathbf{X}$ e $Y$: \[H_0: F_{Y \mid \mathbf{X}} = F_Y\] o equivalentemente que $\mathbf{X}$ no influye en la distribución de $Y$.

En este caso los valores de la respuesta serían intercambiables bajo la hipótesis nula, por lo que podríamos obtener las remuestras manteniendo fijos los valores³³ $\mathbf{X}_i$ y permutando los $Y_i$. Es decir:

Generar $Y^{\ast}_i$, con $i=1,\ldots, n$, mediante muestreo sin reemplazamiento de $\left\{ Y_i: i=1,\ldots, n \right\}$.
Considerar la remuestra bootstrap $\left\{ \left( \mathbf{X}_i, Y^{\ast}_i\right): i=1,\ldots, n \right\}$.

Se pueden realizar contrastes de este tipo con el paquete boot estableciendo el parámetro sim = "permutation" al llamar a la función boot() (el argumento i de la función statistic contendrá permutaciones del vector de índices). Puede ser también de interés el paquete coin, que implementa muchos contrastes de este tipo.

Ejemplo 10.4 (Inferencia sobre el coeficiente de correlación lineal)

Continuando con el ejemplo de las secciones 8.3.3 y 10.2.6 (y de los Ejercicios 8.1, 10.1 y 10.2), estamos interesados en hacer inferencia sobre el coeficiente de correlación lineal $\rho$ empleando el coeficiente de correlación muestral $r$ como estimador. En este caso sin embargo, consideraremos como ejemplo el conjunto de datos dogs del paquete boot, que contiene observaciones sobre el consumo de oxígeno cardíaco (mvo) y la presión ventricular izquierda (lvp) de 7 perros domésticos.

library(boot)
data('dogs', package = "boot")
# plot(dogs)
cor(dogs$mvo, dogs$lvp)

## [1] 0.8536946

# with(dogs, cor(mvo, lvp))

Como ya se comentó, para realizar inferencias sobre $\rho$ podemos emplear la función cor.test():

cor.test(dogs$mvo, dogs$lvp)

## 
##  Pearson's product-moment correlation
## 
## data:  dogs$mvo and dogs$lvp
## t = 3.6655, df = 5, p-value = 0.01451
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.2818014 0.9780088
## sample estimates:
##       cor 
## 0.8536946

# with(dogs, cor.test(mvo, lvp))

Esta función realiza el contraste $H_0: \rho = 0$ empleando el estadístico: \[\frac{r\sqrt{n - 2}}{\sqrt{1 - r^2}} \underset{aprox}{\sim } t_{n-2},\] bajo la hipótesis nula de que la verdadera correlación es cero. Alternativamente se pueden realizar contrastes unilaterales estableciendo el parámetro alternative igual a "less" o "greater". Por ejemplo, para contrastar $H_0: \rho \leq 0$ podríamos emplear:

cor.test(dogs$mvo, dogs$lvp, alternative = "greater")

## 
##  Pearson's product-moment correlation
## 
## data:  dogs$mvo and dogs$lvp
## t = 3.6655, df = 5, p-value = 0.007255
## alternative hypothesis: true correlation is greater than 0
## 95 percent confidence interval:
##  0.4195889 1.0000000
## sample estimates:
##       cor 
## 0.8536946

Para realizar el contraste con la función boot podríamos emplear el siguiente código:

library(boot)

statistic <- function(data, i) cor(data$mvo, data$lvp[i])

set.seed(1)
res.boot <- boot(dogs, statistic, R = 1000, sim = "permutation")
# res.boot

Posteriormente emplearíamos las réplicas (almacenadas en res.boot$t) y el valor observado del estadístico del contraste (almacenado en res.boot$t0) para aproximar el $p$-valor:

hist(res.boot$t, freq = FALSE, main ="")
abline(v = res.boot$t0, lty = 2)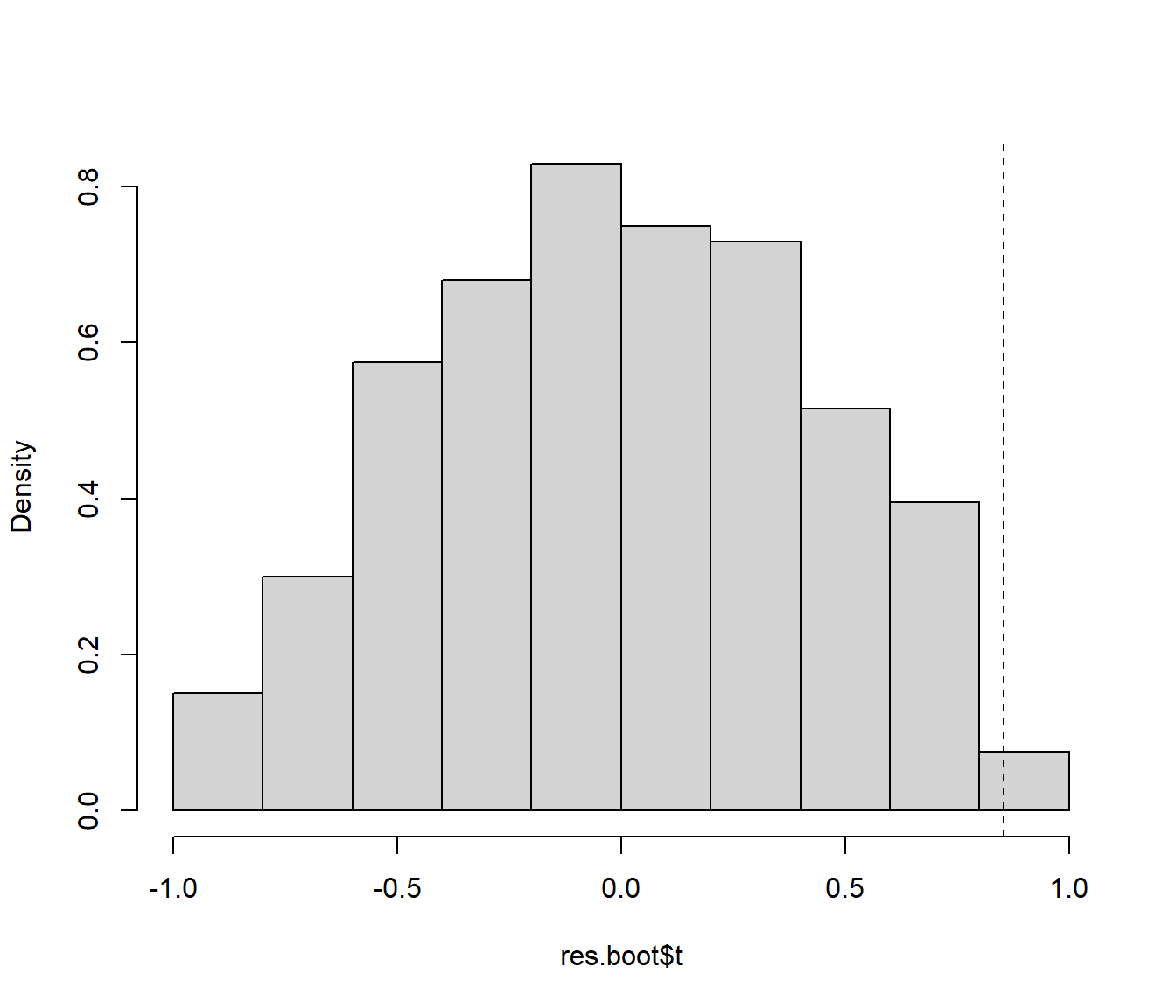

Figura 10.4: Distribución del estadístico del contraste bajo la hipótesis nula aproximada mediante permutación de las observaciones.

Por ejemplo, para el contraste unilateral $H_0: \rho \leq 0$ (alternative = "greater"), obtendríamos:

pval.greater <- mean(res.boot$t >= res.boot$t0)
pval.greater

## [1] 0.009

Mientras que para realizar el contraste bilateral $H_0: \rho = 0$ (alternative = "two.sided"), sin asumir que la distribución del estadístico de contraste es simétrica:

pval.less <- mean(res.boot$t <= res.boot$t0)
pval <- 2*min(pval.less, pval.greater)
pval

## [1] 0.018

10.3.3 Contrastes bootstrap semiparamétricos

Este tipo de aproximación se emplearía en el caso de que la hipótesis nula (o la alternativa) especifique un modelo semiparamétrico, con una componente paramétrica y otra no paramétrica. Típicamente se incluye el error en la componente no paramétrica, y podríamos emplear el bootstrap residual (también denominado semiparamétrico o basado en modelos) descrito en la Sección 9.4.2.

En esta sección nos centraremos en inferencia sobre modelos de regresión lineales (aunque el procedimiento sería análogo en el caso de modelos más generales), empleando como ejemplo el conjunto de datos Prestige del paquete carData, considerando como variable respuesta prestige (puntuación de ocupaciones obtenidas a partir de una encuesta) y como variables explicativas: income (media de ingresos en la ocupación) y education (media de los años de educación).

data(Prestige, package = "carData")
# ?Prestige

En la mayoría de los casos nos interesa contrastar un modelo reducido frente a un modelo completo (que generaliza el modelo reducido). Por ejemplo, en el caso de modelos lineales (estimados por mínimos cuadrados) se dispone del test $F$ para realizar los contrastes de este tipo, que emplea el estadístico: \[F=\frac{n - q}{q - q_0}\frac{RSS_0 - RSS}{RSS},\] siendo $n$ el número de observaciones, $RSS$ y $q$ la suma de cuadrados residual y el número de parámetros distintos del modelo completo, y $RSS_0$ y $q_0$ los correspondientes al modelo reducido. Este estadístico sigue una distribución $\mathcal{F}_{q - q_0, n - q}$ bajo $H_0$ y las hipótesis habituales del modelo lineal ($\varepsilon_i$ i.i.d. $\mathcal{N}(0, \sigma^2)$).

El contraste de regresión sería un caso particular. Por ejemplo, para contrastar si income y education influyen linealmente en prestige podemos emplear el siguiente código:

modelo <- lm(prestige ~ income + education, data = Prestige)
summary(modelo)

## 
## Call:
## lm(formula = prestige ~ income + education, data = Prestige)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -19.4040  -5.3308   0.0154   4.9803  17.6889 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -6.8477787  3.2189771  -2.127   0.0359 *  
## income       0.0013612  0.0002242   6.071 2.36e-08 ***
## education    4.1374444  0.3489120  11.858  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 7.81 on 99 degrees of freedom
## Multiple R-squared:  0.798,  Adjusted R-squared:  0.7939 
## F-statistic: 195.6 on 2 and 99 DF,  p-value: < 2.2e-16

También podemos obtener el valor observado del estadístico $F$ a partir de los resultados del método summary.lm():

res <- summary(modelo)
# names(res)
stat <- res$fstatistic[1]
df <- res$fstatistic[2]
dfr <- res$fstatistic[3]
res$fstatistic

##    value    numdf    dendf 
## 195.5505   2.0000  99.0000

o haciendo los cálculos a mano:

n <- nrow(Prestige)
q <- 3
q0 <- 1
rss0 <- with(Prestige, sum((prestige - mean(prestige))^2))
rss <- sum(residuals(modelo)^2)
inc.mse <- (rss0 - rss)/(q - q0)  # Incremento en varibilidad explicada
msr <-  rss/(n - q)               # Variabilidad residual
inc.mse/msr

## [1] 195.5505

Desde el punto de vista de comparación de modelos, el modelo reducido bajo la hipótesis nula es:

modelo0 <- lm(prestige ~ 1, data = Prestige)

y podemos realizar el contraste mediante la función anova()

anova(modelo0, modelo)

## Analysis of Variance Table
## 
## Model 1: prestige ~ 1
## Model 2: prestige ~ income + education
##   Res.Df     RSS Df Sum of Sq      F    Pr(>F)    
## 1    101 29895.4                                  
## 2     99  6038.9  2     23857 195.55 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Para aproximar la distribución de este estadístico bajo $H_0$ podríamos adaptar el bootstrap semiparamétrico³⁴ descrito en la Sección 9.4.2:

library(boot)

pres.dat <- Prestige
# pres.dat$fit0 <- mean(Prestige$prestige)
# pres.dat$fit0 <- predict(modelo0)
pres.dat$res0 <- with(Prestige, prestige - mean(prestige))
# pres.dat$res0 <- residuals(modelo0)

mod.stat <- function(data, i) {
    data$prestige <- mean(data$prestige) + data$res0[i]
    fit <- lm(prestige ~ income + education, data = data)
    summary(fit)$fstatistic[1]
}

set.seed(1)
boot.mod <- boot(pres.dat, mod.stat, R = 1000)
boot.mod

## 
## ORDINARY NONPARAMETRIC BOOTSTRAP
## 
## 
## Call:
## boot(data = pres.dat, statistic = mod.stat, R = 1000)
## 
## 
## Bootstrap Statistics :
##     original    bias    std. error
## t1* 195.5505 -194.4866    1.096335

hist(boot.mod$t, freq = FALSE, breaks = "FD", main = "")
curve(pf(x, df, dfr, lower.tail = FALSE), lty = 2, add = TRUE)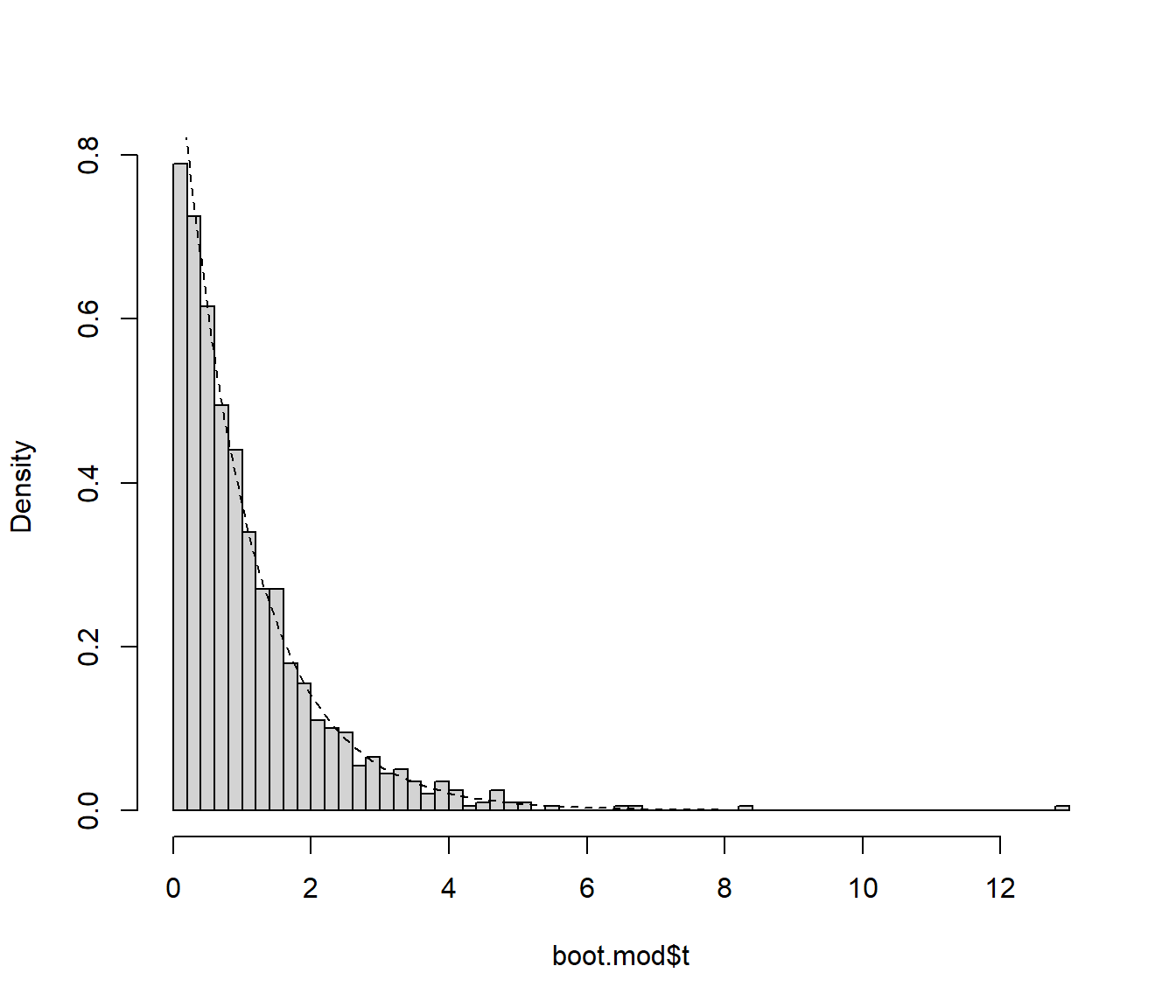

Figura 10.5: Distribución del estadístico del contraste (bajo la hipótesis nula) aproximada mediante bootstrap semiparamétrico.

# pval <- mean(boot.mod$t >= boot.mod$t0)
pval <- mean(boot.mod$t >= stat)
pval

## [1] 0

Procediendo de esta forma sin embargo estaríamos sobreestimando la variabilidad del error cuando la hipótesis nula es falsa (la variabilidad no explicada por la tendencia es asumida por el error), lo que disminuirá la potencia del contraste. Para mejorar la potencia, siguiendo la idea propuesta por González-Manteiga y Cao (1993), se pueden remuestrear los residuos del modelo completo. De esta forma reproduciríamos la variabilidad del error de forma consistente tanto bajo la hipótesis alternativa como bajo la nula.

old.par <- par(mfrow=c(1,2))
# Variabilidad residual con el modelo reducido
hist(residuals(modelo0), xlim = c(-50, 50), main = "")
# Variabilidad residual con el modelo completo
hist(residuals(modelo), xlim = c(-50, 50), main = "")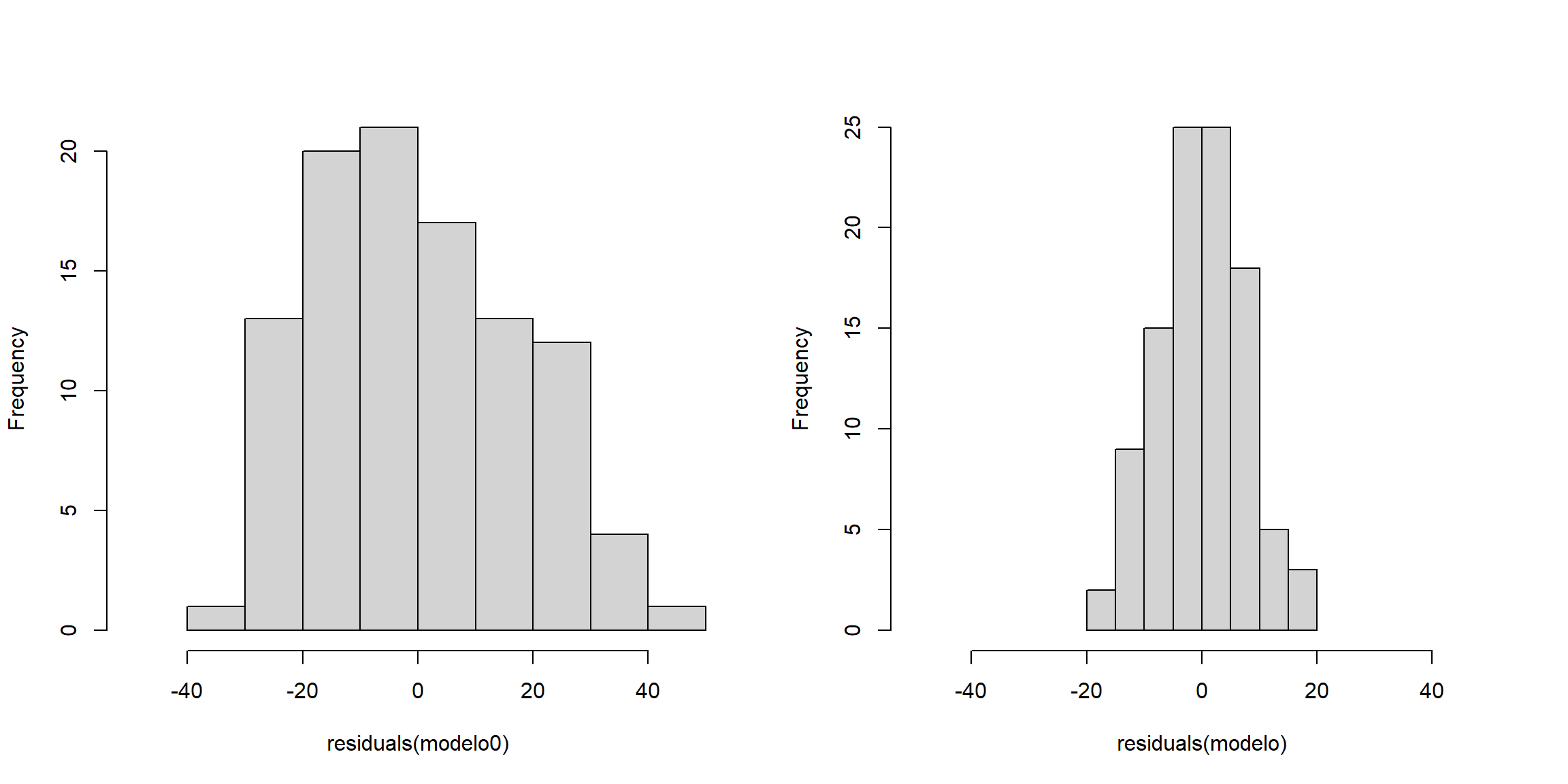

Figura 10.6: Variabilidad residual con el modelo reducido (izquierda) y con el modelo completo (derecha).

par(old.par)

Adicionalmente, como se mostró en la Sección 9.4.2, se puede emplear la modificación propuesta en Davison y Hinkley (1997, Alg. 6.3, p. 271) y remuestrear los residuos reescalados y centrados.

pres.dat <- Prestige
# pres.dat$fit0 <- mean(Prestige$prestige)
# pres.dat$fit0 <- predict(modelo0)
# pres.dat$res <- residuals(modelo)
pres.dat$sres <- residuals(modelo)/sqrt(1 - hatvalues(modelo))
pres.dat$sres <- pres.dat$sres - mean(pres.dat$sres)

mod.stat <- function(data, i) {
    # data$prestige <- mean(data$prestige) + data$res[i]
    data$prestige <- mean(data$prestige) + data$sres[i]
    fit <- lm(prestige ~ income + education, data = data)
    summary(fit)$fstatistic[1]
}

set.seed(1)
boot.mod <- boot(pres.dat, mod.stat, R = 1000)
boot.mod

## 
## ORDINARY NONPARAMETRIC BOOTSTRAP
## 
## 
## Call:
## boot(data = pres.dat, statistic = mod.stat, R = 1000)
## 
## 
## Bootstrap Statistics :
##       original   bias    std. error
## t1* 0.01164396 1.029746    1.029715

En la aproximación del $p$-valor hay que tener en cuenta que al modificar los residuos boot.mod$t0 no va a coincidir con el valor observado del estadístico, almacenado en stat (por tanto habría que ignorar original y bias en Bootstrap Statistics; la función Boot() del paquete car corrige este problema).

hist(boot.mod$t, freq = FALSE, breaks = "FD", main = "")
curve(pf(x, df, dfr, lower.tail = FALSE), lty = 2, add = TRUE)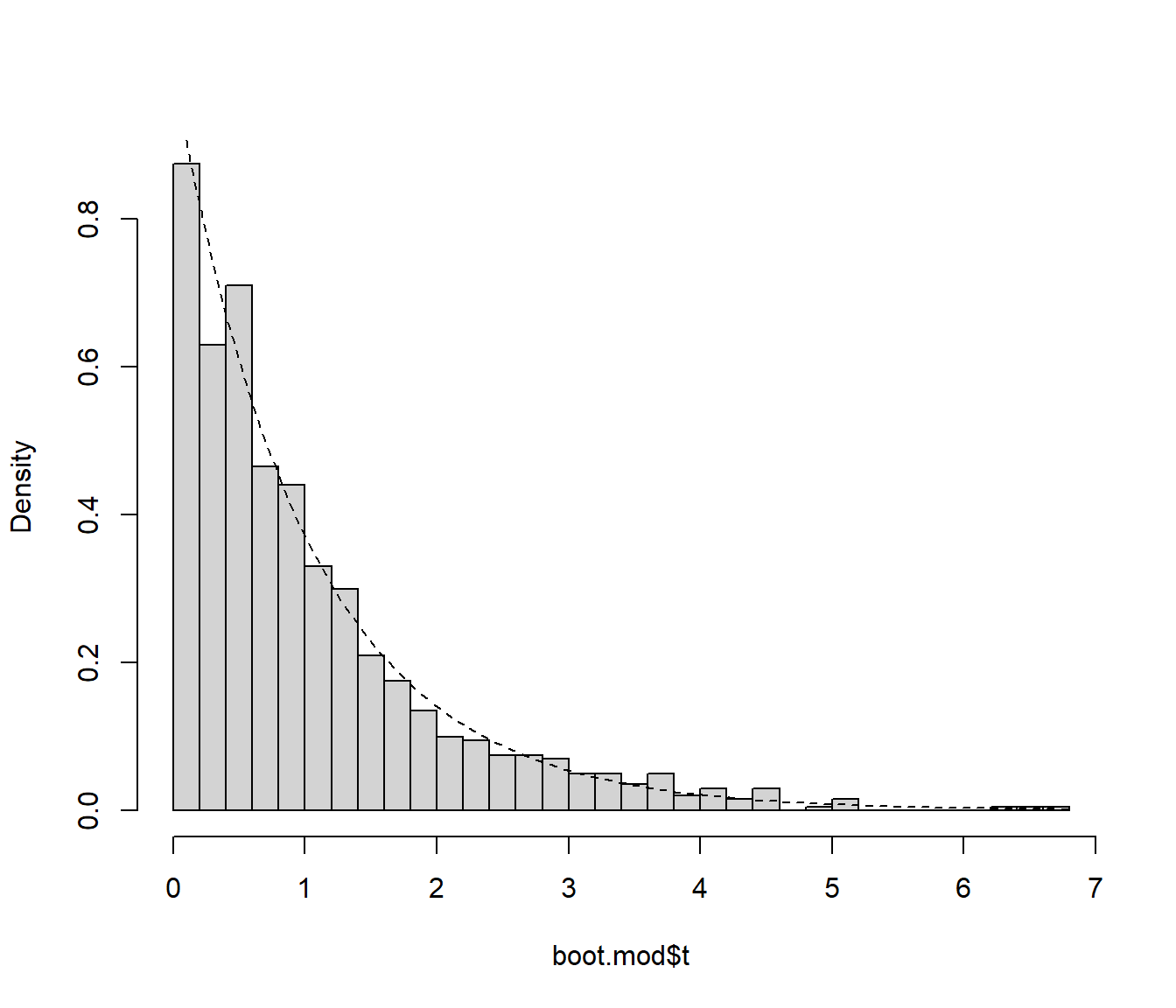

Figura 10.7: Distribución del estadístico del contraste (bajo la hipótesis nula) aproximada mediante bootstrap semiparamétrico.

pval <- mean(boot.mod$t >= stat)
pval

## [1] 0

En el caso de modelos no lineales (o otros tipos de modelos lineales) puede ser complicado aproximar los grados de libertad para el cálculo del estadístico $F$, pero si empleamos bootstrap, vamos a obtener los mismos resultados considerando como estadístico: \[\tilde F =\frac{RSS_0 - RSS}{RSS},\] que se puede interpretar también como una medida del incremento en la variabilidad residual al considerar el modelo reducido (ya que únicamente difieren en una constante). En este caso también se suelen emplear los residuos sin reescalar, ya que también puede ser difícil encontrar la transformación adecuada.

Ejercicio 10.3

Al estudiar el efecto de las variables explicativas en el modelo anterior, podríamos pensar que no es adecuado asumir un efecto lineal de alguna de las variables explicativas. Por ejemplo, si generamos los gráficos parciales de residuos obtendríamos:

car::crPlots(modelo)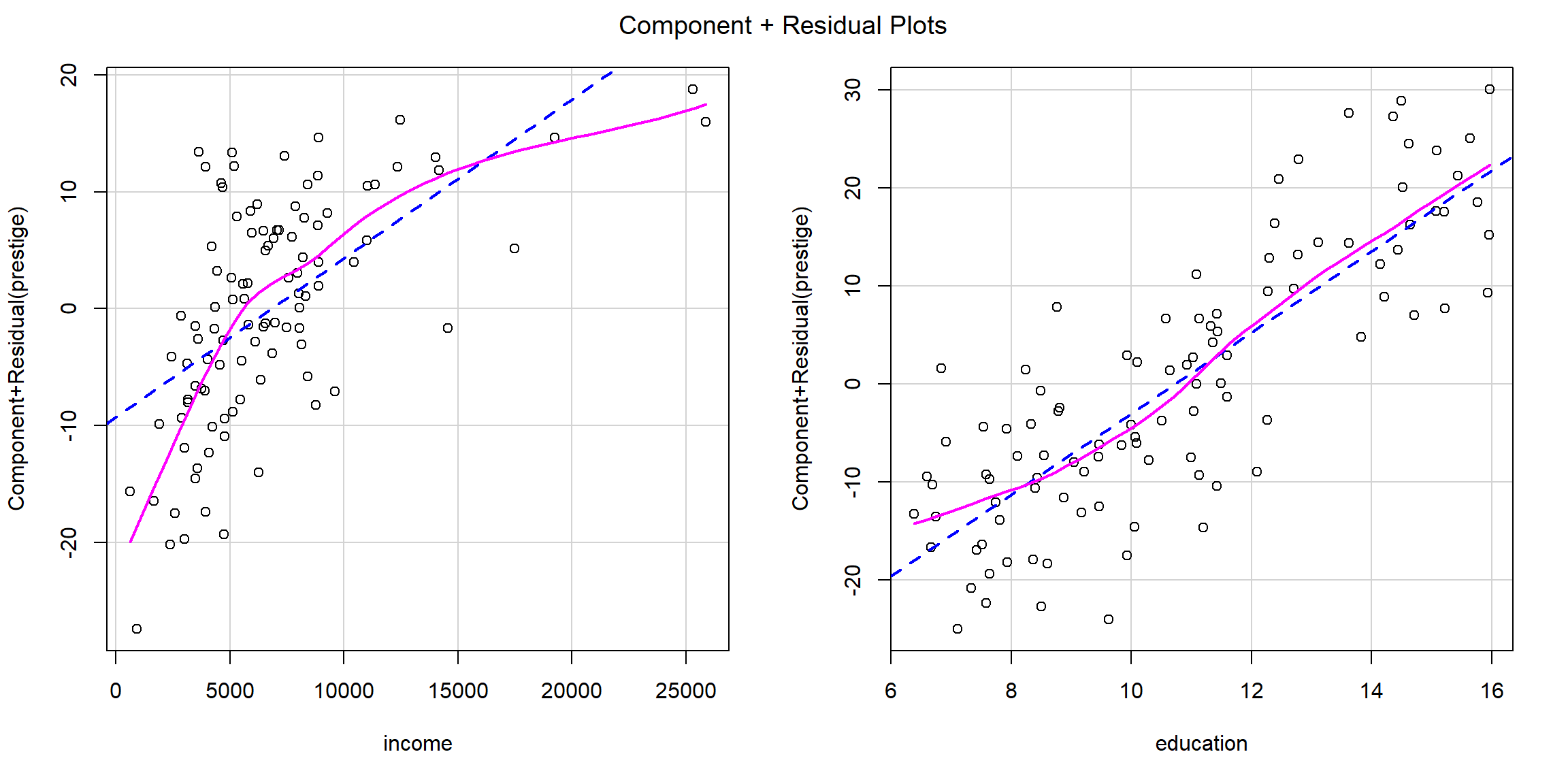

Figura 10.8: Efecto de las variables explicativas en el modelo (gráficos de residuos).

En este caso podría ser razonable considerar un efecto cuadrático de la variable income³⁵

modelo <- lm(prestige ~ income + I(income^2) + education, data = Prestige)
summary(modelo)

## 
## Call:
## lm(formula = prestige ~ income + I(income^2) + education, data = Prestige)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -15.732  -4.900  -0.057   4.598  18.459 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -1.135e+01  3.272e+00  -3.470 0.000775 ***
## income       3.294e-03  5.669e-04   5.810 7.79e-08 ***
## I(income^2) -7.967e-08  2.169e-08  -3.673 0.000390 ***
## education    3.809e+00  3.407e-01  11.179  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 7.36 on 98 degrees of freedom
## Multiple R-squared:  0.8224, Adjusted R-squared:  0.817 
## F-statistic: 151.3 on 3 and 98 DF,  p-value: < 2.2e-16

Para comparar el ajuste de este modelo respecto al del anterior, podemos realizar un contraste empleando la función anova():

modelo0 <- lm(prestige ~ income + education, data = Prestige)
anova(modelo0, modelo)

## Analysis of Variance Table
## 
## Model 1: prestige ~ income + education
## Model 2: prestige ~ income + I(income^2) + education
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1     99 6038.9                                  
## 2     98 5308.0  1     730.8 13.492 0.0003904 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Contrastar si el efecto de income es lineal mediante bootstrap residual, empleando como estadístico el incremento en la variabilidad residual con el modelo reducido y remuestreando los residuos del modelo completo (sin reescalar). Aproximar el nivel crítico del contraste y el valor que tendría que superar el estadístico para rechazar $H_0$ con un nivel de significación $\alpha = 0.05$.

Aunque cuando la hipótesis nula es compuesta: $P\left( D\in RR \mid H_0\text{ cierta}\right) \leq \alpha$.↩︎
Nótese que no se hace ninguna suposición sobre el tipo de covariables, podrían ser categóricas, numéricas o una combinación de ambas.↩︎
En este caso también podríamos emplear un contraste de permutaciones.↩︎
Para ajustar un modelo polinómico puede ser recomendable, especialmente si el grado del polinomio es alto, emplear la función poly() ya que utiliza polinomios ortogonales. En el caso cuadrático, al emplear y ~ x + I(x^2) estaremos considerando $1, x, x^2$, mientras que y ~ poly(x, 2) considerará polinomios de Legendre de la forma $1, x, \frac{1}{2}(3x^2-1)$. En este caso concreto, obtendríamos una parametrización equivalente empleando modelo <- lm(prestige ~ poly(income, 2) + education, data = Prestige).↩︎