6.1 Simulación de componentes independientes
Si las componentes son independientes y \(f_i\) son las correspondientes densidades marginales, bastará con generar \(X_i \sim f_i\). Las dificultades aparecerán cuando se quiera simular componentes con una determinada estructura de dependencia.
Ejemplo 6.1 (simulación de normales independientes)
Si \(\boldsymbol\mu =\left( \mu_1,\mu_2,\ldots,\mu_d\right)^t\) es un vector (de medias) y \(\Sigma\) es una matriz \(d \times d\) definida positiva (de varianzas-covarianzas), el vector aleatorio \(\mathbf{X}\) sigue una distribución normal multivariante con esos parámetros, \(\mathbf{X} \sim \mathcal{N}_d\left( \boldsymbol\mu,\Sigma \right)\), si su función de densidad es de la forma: \[f(\mathbf x) = \frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}} \exp \left( -\frac{1}{2} ( \mathbf x - \boldsymbol \mu)^t \Sigma^{-1} (\mathbf x - \boldsymbol \mu) \right),\] donde \(| \Sigma |\) es el determinante de \(\Sigma\).
Si la matriz de covarianzas es diagonal \(\Sigma=diag\left( \sigma_1^2,\sigma_2^2,\ldots,\sigma_d^2\right)\), entonces las componentes \(X_i \sim \mathcal{N}\left( \mu_i,\sigma_i^2\right)\) son independientes y podemos simular el vector aleatorio de forma trivial, por ejemplo mediante el siguiente algoritmo:
Algoritmo 6.1 (de simulación de normales independientes)
Simular \(Z_1, Z_2, \ldots, Z_d \sim \mathcal{N} \left( 0, 1 \right)\) independientes.
Para \(i = 1, 2, \ldots, d\) hacer \(X_i = \mu_i + \sigma_i Z_i\).
Las funciones implementadas en el paquete base de R permiten simular fácilmente en el caso independiente ya que admiten vectores como parámetros. Por ejemplo en el caso bidimensional con \(X_1 \sim \mathcal{N}\left( 0, 1\right)\) y \(X_2 \sim \mathcal{N}\left( -1, 0.5^2 \right)\):
f1 <- function(x) dnorm(x)
f2 <- function(x) dnorm(x, -1, 0.5)
curve(f1, -3, 3, ylim = c(0, f2(-1)), ylab = "fdp")
curve(f2, add = TRUE, lty = 2)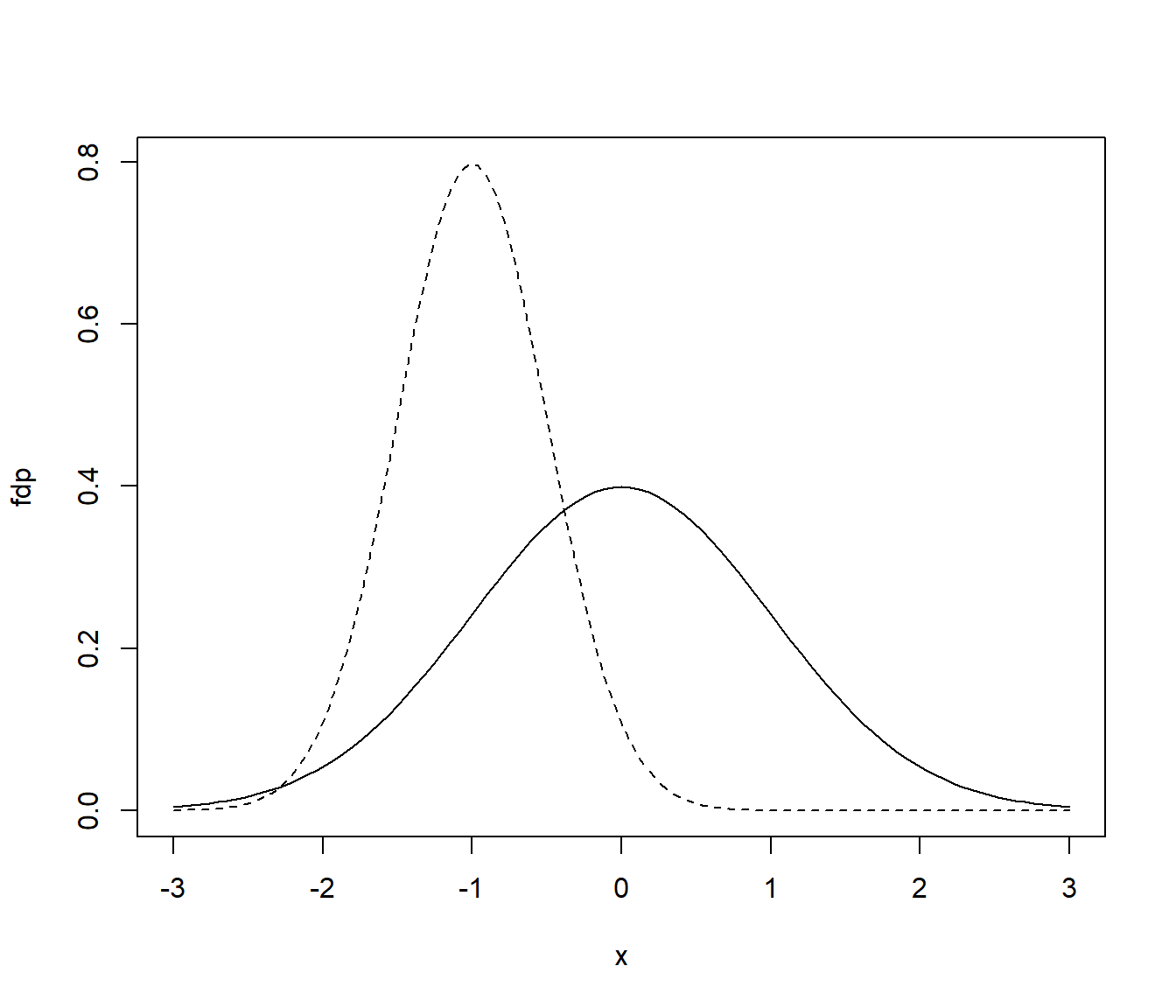
Figura 6.1: Densidades marginales de las componentes del Ejemplo 6.1.
Para simular una generación bastaría con:
set.seed(1)
rnorm(2, c(0, -1), c(1, 0.5))## [1] -0.6264538 -0.9081783y para simular nsim:
set.seed(1)
nsim <- 5
rx <- matrix(rnorm(2*nsim, c(0, -1), c(1, 0.5)), nrow = nsim, byrow = TRUE)
colnames(rx) <- paste0("X", 1:ncol(rx))
rx## X1 X2
## [1,] -0.6264538 -0.9081783
## [2,] -0.8356286 -0.2023596
## [3,] 0.3295078 -1.4102342
## [4,] 0.4874291 -0.6308376
## [5,] 0.5757814 -1.1526942