1.1 Conceptos básicos

La experimentación directa sobre la realidad puede tener muchos inconvenientes, entre otros:

  • Coste elevado: por ejemplo cuando las pruebas son destructivas o si es necesario esperar mucho tiempo para observar los resultados.

  • Puede no ser ética: por ejemplo la experimentación sobre seres humanos o la dispersión de un contaminante.

  • Puede resultar imposible: por ejemplo cuando se trata de un acontecimiento futuro o una alternativa en el pasado.

Además la realidad puede ser demasiado compleja como para ser estudiada directamente y resultar preferible trabajar con un modelo del sistema real. Un modelo no es más que un conjunto de variables junto con ecuaciones matemáticas que las relacionan y restricciones sobre dichas variables. Habría dos tipos de modelos:

  • Modelos deterministas: en los que bajo las mismas condiciones (fijados los valores de las variables explicativas) se obtienen siempre los mismos resultados.

  • Modelos estocásticos (con componente aleatoria): tienen en cuenta la incertidumbre asociada al modelo. Tradicionalmente se supone que esta incertidumbre es debida a que no se dispone de toda la información sobre las variables que influyen en el fenómeno en estudio (puede ser debida simplemente a que haya errores de medida), lo que se conoce como aleatoriedad aparente:

    “Nothing in Nature is random… a thing appears random only through the incompleteness of our knowledge.”

    — Spinoza, Baruch (Ethics, 1677)

    aunque hoy en día gana peso la idea de la física cuántica de que en el fondo hay una aleatoriedad intrínseca1.

La modelización es una etapa presente en la mayor parte de los trabajos de investigación, especialmente en las ciencias experimentales. El modelo debería considerar las variables más relevantes para explicar el fenómeno en estudio y las principales relaciones entre ellas. La inferencia estadística proporciona herramientas para estimar los parámetros y contrastar la validez de un modelo estocástico a partir de los datos observados.

La idea es emplear el modelo, asumiendo que es válido, para resolver el problema de interés. Si se puede obtener la solución de forma analítica, esta suele ser exacta (aunque en ocasiones solo se dispone de soluciones aproximadas, basadas en resultados asintóticos, o que dependen de suposiciones que pueden ser cuestionables) y a menudo la resolución también es rápida. Cuando la solución no se puede obtener de modo analítico (o si la aproximación disponible no es adecuada) se puede recurrir a la simulación. De esta forma se pueden obtener resultados para un conjunto más amplio de modelos, que pueden ser mucho más complejos.

Nos centraremos en el caso de la simulación estocástica: las conclusiones se obtienen generando repetidamente simulaciones del modelo aleatorio. Muchas veces se emplea la denominación de método Monte Carlo2 como sinónimo de simulación estocástica, pero realmente se trata de métodos especializados que emplean simulación para resolver problemas que pueden no estar relacionados con un modelo estocástico de un sistema real. Por ejemplo, en el Capítulo 7 se tratarán métodos de integración y optimización Monte Carlo.

1.1.1 Ejemplo

Supongamos que nos regalan un álbum con \(n = 75\) cromos, que se venden sobres con \(m = 6\) cromos por 0.8€, y que estamos interesados en el número de sobres que hay que comprar para completar la colección, por ejemplo en su valor medio.

Podemos aproximar la distribución del número de sobres para completar la colección a partir de \(nsim=1000\) simulaciones de coleccionistas de cromos:

# Parámetros
n <- 75 # Número total de cromos
m <- 6  # Número de cromos en cada sobre
repe <- TRUE # Repetición de cromos en cada sobre
# Número de simulaciones
nsim <- 1000
# Resultados simulación
nsobres <- numeric(nsim)
# evol <- vector("list", nsim)
# Fijar semilla
set.seed(1)
# Bucle simulación
for (isim in 1:nsim) {
  # seed <- .Random.seed    # .Random.seed <- seed
  album <- logical(n)
  i <- 0 # Número de sobres
  while(sum(album) < n) {
    i <- i + 1
    album[sample(n,m, replace = repe)] <- TRUE
  }
  nsobres[isim] <- i
}

Distribución del número de sobres para completar la colección (aproximada por simulación):

hist(nsobres, breaks = "FD", freq = FALSE,
     main = "", xlab = "Número de sobres")
lines(density(nsobres))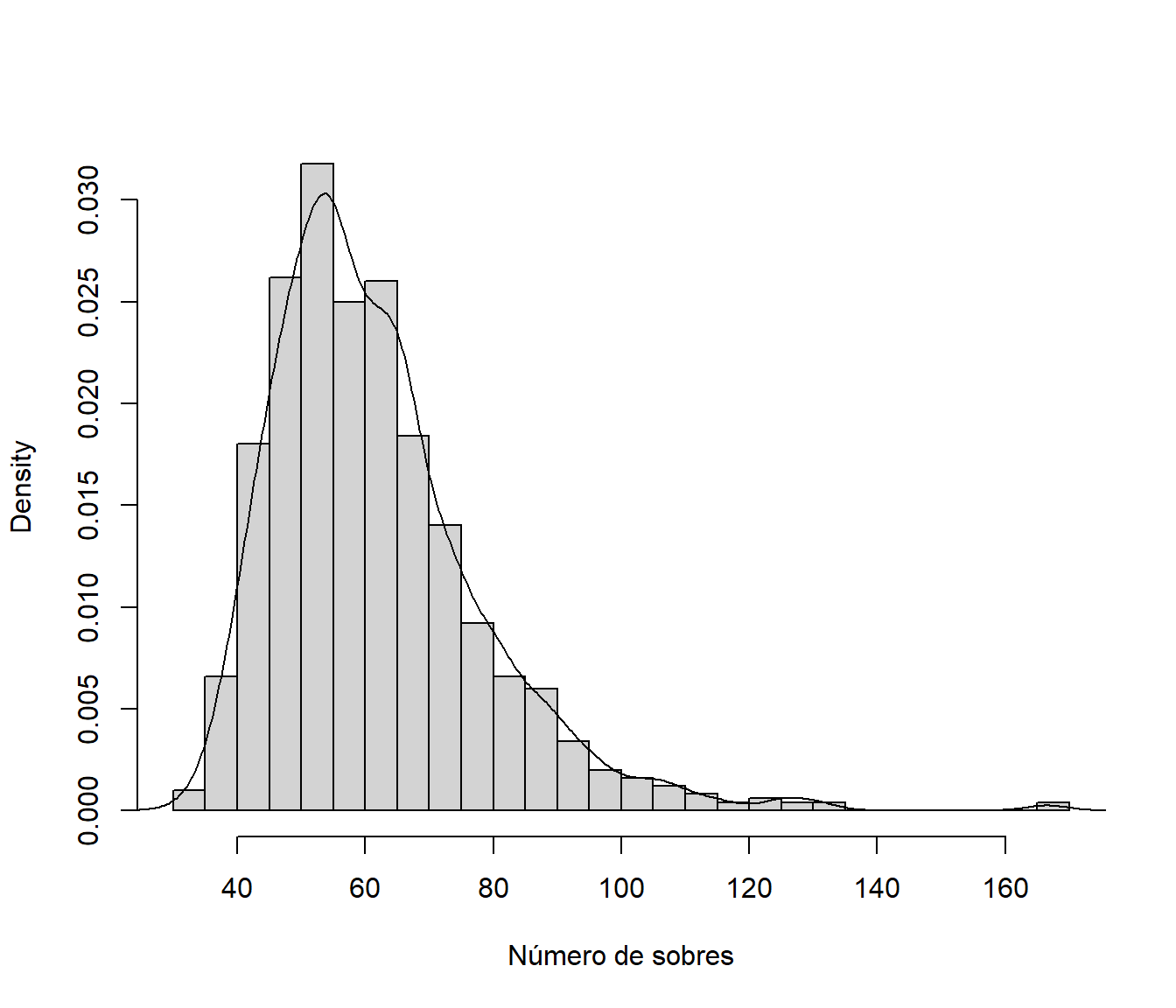
Aproximación por simulación de la distribución del número de sobres para completar la colección.

Figura 1.1: Aproximación por simulación de la distribución del número de sobres para completar la colección.

Aproximación por simulación del número medio de sobres para completar la colección:

sol <- mean(nsobres)
sol
## [1] 61.775

Número mínimo de sobres para asegurar de que se completa la colección con una probabilidad del 95%:

nmin <- quantile(nsobres, probs = 0.95)
ceiling(nmin)
## 95% 
##  92
# Reserva de dinero para poder completar la colección el 95% de las veces:
ceiling(nmin)*0.8
##  95% 
## 73.6
hist(nsobres, breaks = "FD", freq = FALSE,
     main = "", xlab = "Número de sobres")
lines(density(nsobres))
abline(v = sol)
abline(v = nmin, lty = 2)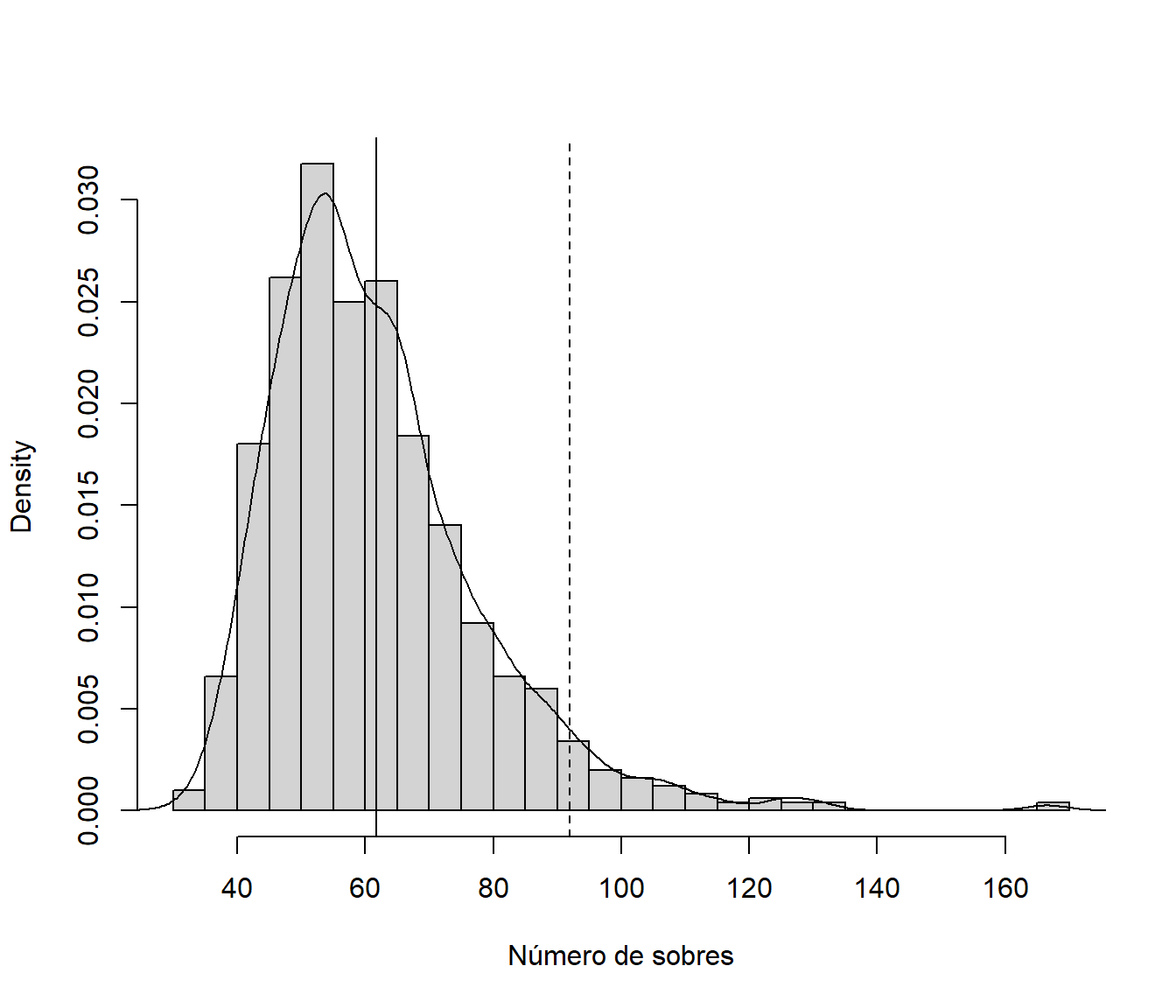
Aproximaciones por simulación de la distribución del número de sobres para completar la colección, de su valor esperado (línea vertical continua) y del cuantil 0.95 (línea vertical discontinua).

Figura 1.2: Aproximaciones por simulación de la distribución del número de sobres para completar la colección, de su valor esperado (línea vertical continua) y del cuantil 0.95 (línea vertical discontinua).

Por supuesto, la distribución del gasto necesario para completar la colección es esta misma reescalada.

res <- simres::mc.plot(nsobres*0.8)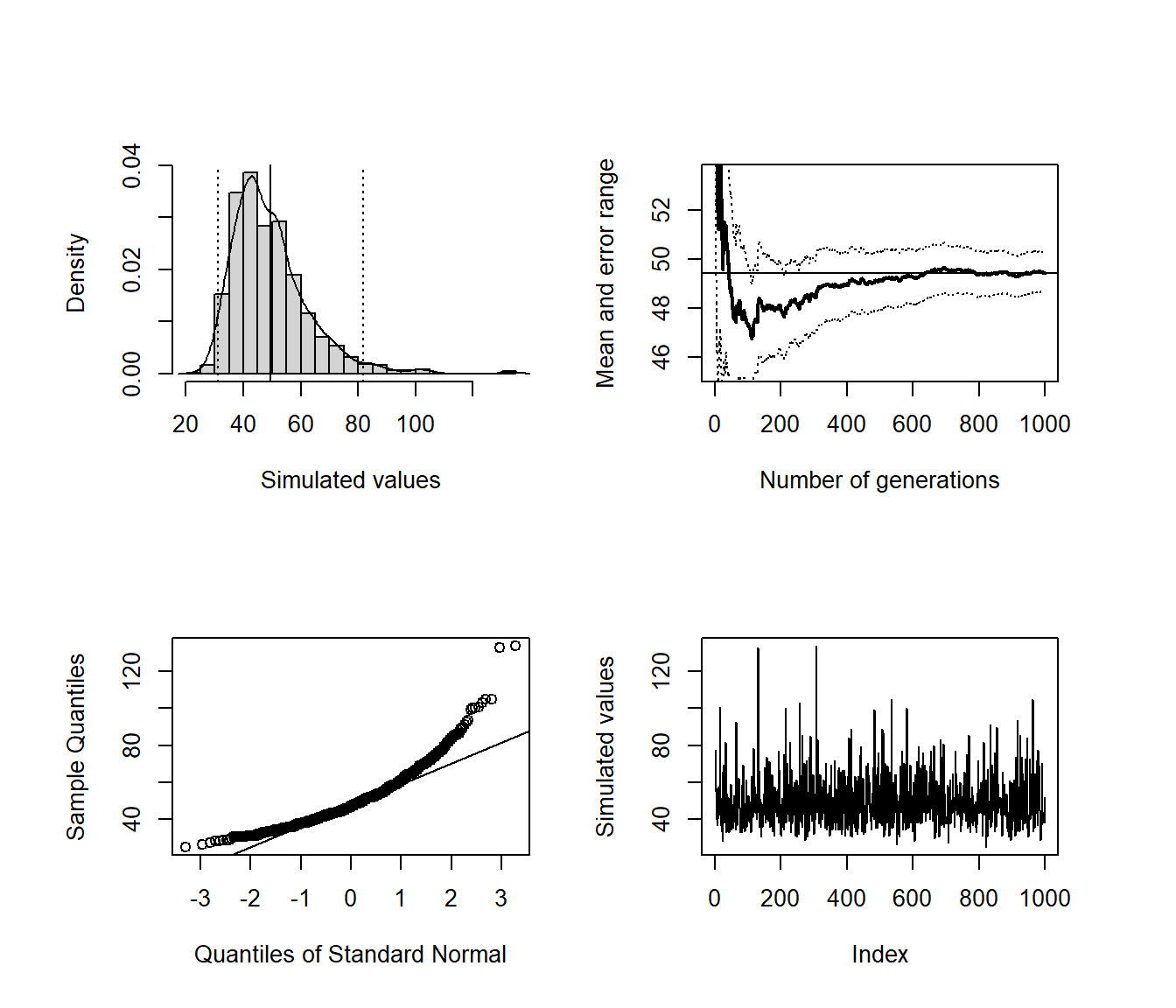
Gráficos exploratorios de las simulaciones del gasto para completar la colección obtenidos con la función `simres::mc.plot()`.

Figura 1.3: Gráficos exploratorios de las simulaciones del gasto para completar la colección obtenidos con la función simres::mc.plot().

Aproximación del gasto medio:

res$approx  # sol*0.8
## [1] 49.42

En el Ejercicio 1.5 se propone modificar este código para obtener información adicional sobre la evolución del número de cromos distintos dependiendo de los sobres comprados por un coleccionista.

1.1.2 Ventajas e inconvenientes de la simulación

Ventajas (Shannon, 1975):

  • Cuando la resolución analítica no puede llevarse a cabo.

  • Cuando existen medios de resolver analíticamente el problema pero dicha resolución es complicada y costosa (o solo proporciona una solución aproximada).

  • Si se desea experimentar antes de que exista el sistema (pruebas para la construcción de un sistema).

  • Cuando es imposible experimentar sobre el sistema real por ser dicha experimentación destructiva.

  • En ocasiones en las que la experimentación sobre el sistema es posible pero no ética.

  • En sistemas que evolucionan muy lentamente en el tiempo.

El principal incoveniente puede ser el tiempo de computación necesario, aunque gracias a la gran potencia de cálculo de los computadores actuales, se puede obtener rápidamente una solución aproximada en la mayor parte de los problemas susceptibles de ser modelizados. Además siempre están presentes los posibles problemas debidos a emplear un modelo:

  • La construcción de un buen modelo puede ser una tarea muy costosa (compleja, laboriosa y requerir mucho tiempo; e.g. modelos climáticos).

  • Frecuentemente el modelo omite variables o relaciones importantes entre ellas (los resultados pueden no ser válidos para el sistema real).

  • Resulta difícil conocer la precisión del modelo formulado.

Otro problema de la simulación es que se obtienen resultados para unos valores concretos de los parámetros del modelo, por lo que en principio resultaría complicado extrapolar las conclusiones a otras situaciones.

1.1.3 Aplicaciones de la simulación

La simulación resulta de utilidad en multitud de contextos diferentes. Los principales campos de aplicación son:

  • Estadística:

    • Muestreo, remuestreo…

    • Aproximación de distribuciones (de estadísticos, estimadores…)

    • Realización de contrastes, intervalos de confianza…

    • Comparación de estimadores, contrastes…

    • Validación teoría (distribución asintótica…)

    • Inferencia Bayesiana

  • Optimización: Algoritmos genéticos, temple simulado…

  • Análisis numérico: Aproximación de integrales, resolución de ecuaciones…

  • Computación: Diseño, verificación y validación de algoritmos…

  • Criptografía: Protocolos de comunicación segura…

  • Física: Simulación de fenómenos naturales…

En los capítulos 7.4 y 7 nos centraremos en algunas de las aplicaciones de utilidad en Estadística.

  1. Como ejemplo, en física cuántica, la ecuación de Schrödinger es un modelo determinista que describe la evolución en el tiempo de la función de onda de un sistema. Sin embargo, como las funciones de onda pueden cambiar de forma aleatoria al realizar una medición, se emplea la regla de Born para modelar las probabilidades de las distintas posibilidades (algo que inicialmente generó rechazo, dió lugar a la famosa frase de Einstein “Dios no juega a los dados,” pero experimentos posteriores parecen confirmar). Por tanto en la práctica se emplea un modelo estocástico.↩︎

  2. Estos métodos surgieron a finales de la década de 1940 como resultado del trabajo realizado por Stanislaw Ulam y John von Neumann en el proyecto Manhattan para el desarrollo de la bomba atómica. Al parecer, como se trataba de una investigación secreta, Nicholas Metropolis sugirió emplear el nombre clave de “Monte-Carlo” en referencia al casino de Monte Carlo de Mónaco.↩︎