7.5 Projection pursuit

Projection pursuit (Friedman y Tukey, 1974) es una técnica de análisis exploratorio de datos multivariantes que busca proyecciones lineales de los datos en espacios de dimensión baja, siguiendo una idea originalmente propuesta en (Kruskal, 1969). Inicialmente se presentó como una técnica gráfica y por ese motivo buscaba proyecciones de dimensión 1 o 2 (proyecciones en rectas o planos), resultando que las direcciones interesantes son aquellas con distribución no normal. La motivación es que cuando se realizan transformaciones lineales lo habitual es que el resultado tenga la apariencia de una distribución normal (por el teorema central del límite), lo cual oculta las singularidades de los datos originales. Se supone que los datos son una trasformación lineal de componentes no gaussianas (variables latentes) y la idea es deshacer esta transformación mediante la optimización de una función objetivo, que en este contexto recibe el nombre de projection index. Aunque con orígenes distintos, projection pursuit es muy similar a independent component analysis (Comon, 1994), una técnica de reducción de la dimensión que, en lugar de buscar como es habitual componentes incorreladas (ortogonales), busca componentes independientes y con distribución no normal (ver por ejemplo la documentación del paquete fastICA).

Hay extensiones de projection pursuit para regresión, clasificación, estimación de la función de densidad, etc.

7.5.1 Regresión por projection pursuit

En el método original de projection pursuit regression (PPR, Friedman y Stuetzle, 1981) se considera el siguiente modelo semiparamétrico \[m(\mathbf{x}) = \sum_{m=1}^M g_m (\alpha_{1m}x_1 + \alpha_{2m}x_2 + \ldots + \alpha_{pm}x_p)\] siendo \(\boldsymbol{\alpha}_m = (\alpha_{1m}, \alpha_{2m}, \ldots, \alpha_{pm})\) vectores de parámetros (desconocidos) de módulo unitario y \(g_m\) funciones suaves (desconocidas), denominadas funciones ridge.

Con esta aproximación se obtiene un modelo muy general que evita los problemas de la maldición de la dimensionalidad. De hecho se trata de un aproximador universal, con \(M\) suficientemente grande y eligiendo adecuadamente las componentes se podría aproximar cualquier función continua. Sin embargo el modelo resultante puede ser muy difícil de interpretar, salvo el caso de \(M=1\) que se corresponde con el denominado single index model empleado habitualmente en Econometría, pero que solo es algo más general que el modelo de regresión lineal múltiple.

El ajuste se este tipo de modelos es en principio un problema muy complejo. Hay que estimar las funciones univariantes \(g_m\) (utilizando un método de suavizado) y los parámetros \(\alpha_{im}\), utilizando como criterio de error \(\mbox{RSS}\). En la práctica se resuelve utilizando un proceso iterativo en el que se van fijando sucesivamente los valores de los parámetros y las funciones ridge (si son estimadas empleando un método que también proporcione estimaciones de su derivada, las actualizaciones de los parámetros se pueden obtener por mínimos cuadrados ponderados).

También se han desarrollado extensiones del método original para el caso de respuesta multivariante: \[m_i(\mathbf{x}) = \beta_{i0} + \sum_{m=1}^M \beta_{im} g_m (\alpha_{1m}x_1 + \alpha_{2m}x_2 + \ldots + \alpha_{pm}x_p)\] reescalando las funciones rigde de forma que tengan media cero y varianza unidad sobre las proyecciones de las observaciones.

Este procedimiento de regresión está muy relacionado con las redes de neuronas artificiales que se tratarán en el siguiente capítulo y que han sido de mayor objeto de estudio y desarrollo en los último años.

7.5.2 Implementación en R

El método PPR (con respuesta multivariante) está implementado en la función ppr() del paquete base de R⁵¹, y es también la empleada por el método "ppr" de caret. Esta función:

ppr(formula, data, nterms, max.terms = nterms, optlevel = 2,
    sm.method = c("supsmu", "spline", "gcvspline"),
    bass = 0, span = 0, df = 5, gcvpen = 1, ...)

va añadiendo términos ridge hasta un máximo de max.terms y posteriormente emplea un método hacia atrás para seleccionar nterms (el argumento optlevel controla como se vuelven a reajustar los términos en cada iteración). Por defecto emplea el super suavizador de Friedman (función supsmu(), con parámetros bass y spam), aunque también admite splines (función smooth.spline(), fijando los grados de libertad con df o seleccionándolos mediante GCV). Para más detalles ver help(ppr).

Continuaremos con el ejemplo del conjunto de datos earth::Ozone1. En primer lugar ajustamos un modelo PPR con dos términos (incrementando el suavizado por defecto de supsmu() siguiendo la recomendación de Venables y Ripley, 2002):

ppreg <- ppr(O3 ~ ., nterms = 2, data = train, bass = 2)
summary(ppreg)

## Call:
## ppr(formula = O3 ~ ., data = train, nterms = 2, bass = 2)
## 
## Goodness of fit:
##  2 terms 
## 4033.668 
## 
## Projection direction vectors ('alpha'):
##          term 1       term 2      
## vh       -0.016617786  0.047417127
## wind     -0.317867945 -0.544266150
## humidity  0.238454606 -0.786483702
## temp      0.892051760 -0.012563393
## ibh      -0.001707214 -0.001794245
## dpg       0.033476907  0.285956216
## ibt       0.205536326  0.026984921
## vis      -0.026255153 -0.014173612
## doy      -0.044819013 -0.010405236
## 
## Coefficients of ridge terms ('beta'):
##   term 1   term 2 
## 6.790447 1.531222

Representamos las funciones rigde (ver Figura 7.23):

oldpar <- par(mfrow = c(1, 2))
plot(ppreg)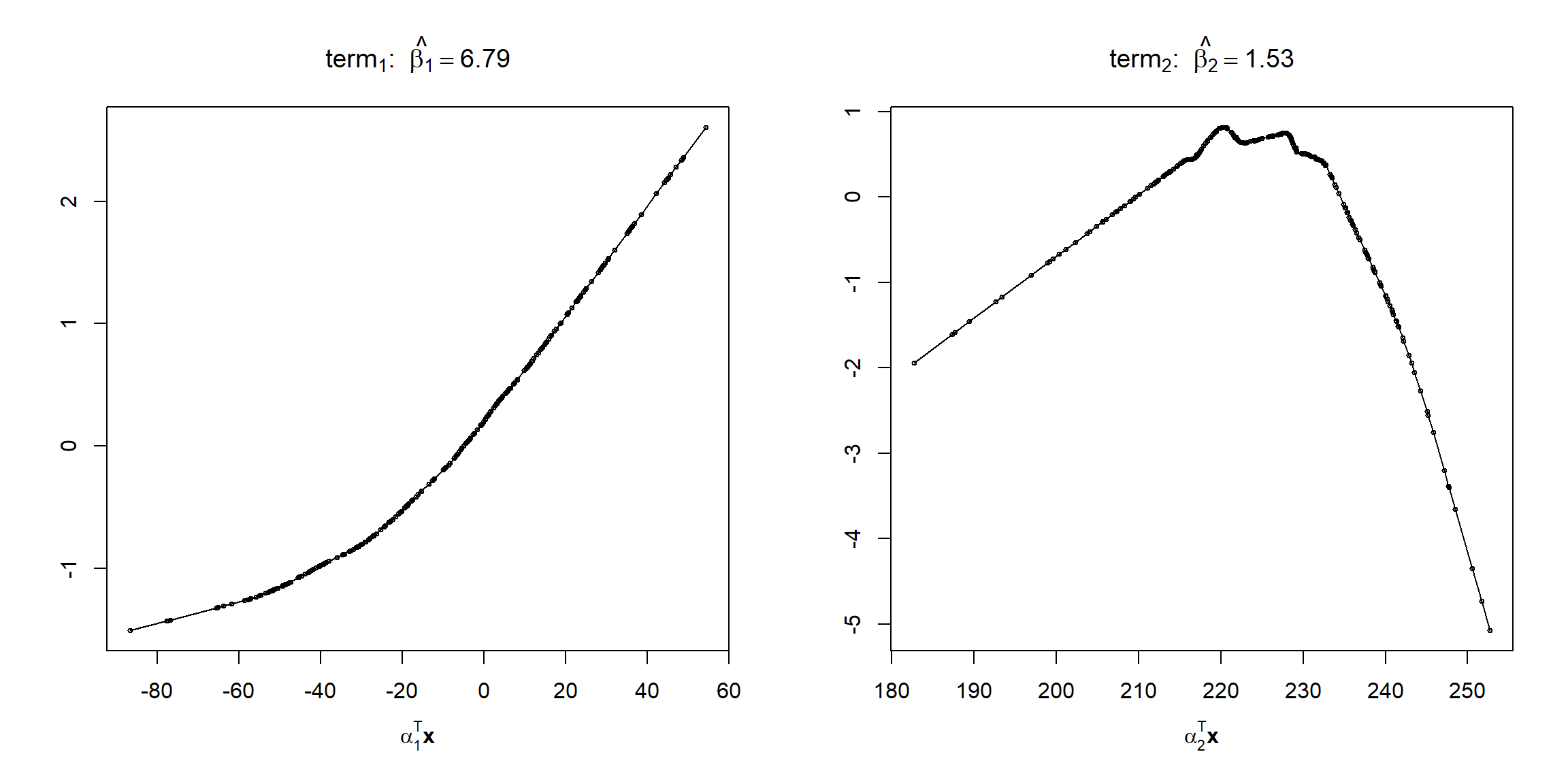

Figura 7.23: Estimaciones de las funciones ridge del ajuste PPR.

par(oldpar)

Evaluamos las predicciones en la muestra de test:

pred <- predict(ppreg, newdata = test)
obs <- test$O3
accuracy(pred, obs)

##         me       rmse        mae        mpe       mape  r.squared 
##  0.4819794  3.2330060  2.5941476 -6.1203121 34.8728543  0.8384607

Podemos emplear el método "ppr" de caret para seleccionar el número de términos (ver Figura 7.24):

library(caret)
modelLookup("ppr")

##   model parameter   label forReg forClass probModel
## 1   ppr    nterms # Terms   TRUE    FALSE     FALSE

set.seed(1)
caret.ppr <- train(O3 ~ ., data = train, method = "ppr", # bass = 2,
    trControl = trainControl(method = "cv", number = 10))
caret.ppr

## Projection Pursuit Regression 
## 
## 264 samples
##   9 predictor
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 238, 238, 238, 236, 237, 239, ... 
## Resampling results across tuning parameters:
## 
##   nterms  RMSE      Rsquared   MAE     
##   1       4.366022  0.7069042  3.306658
##   2       4.479282  0.6914678  3.454853
##   3       4.624943  0.6644089  3.568929
## 
## RMSE was used to select the optimal model using the smallest value.
## The final value used for the model was nterms = 1.

ggplot(caret.ppr, highlight = TRUE)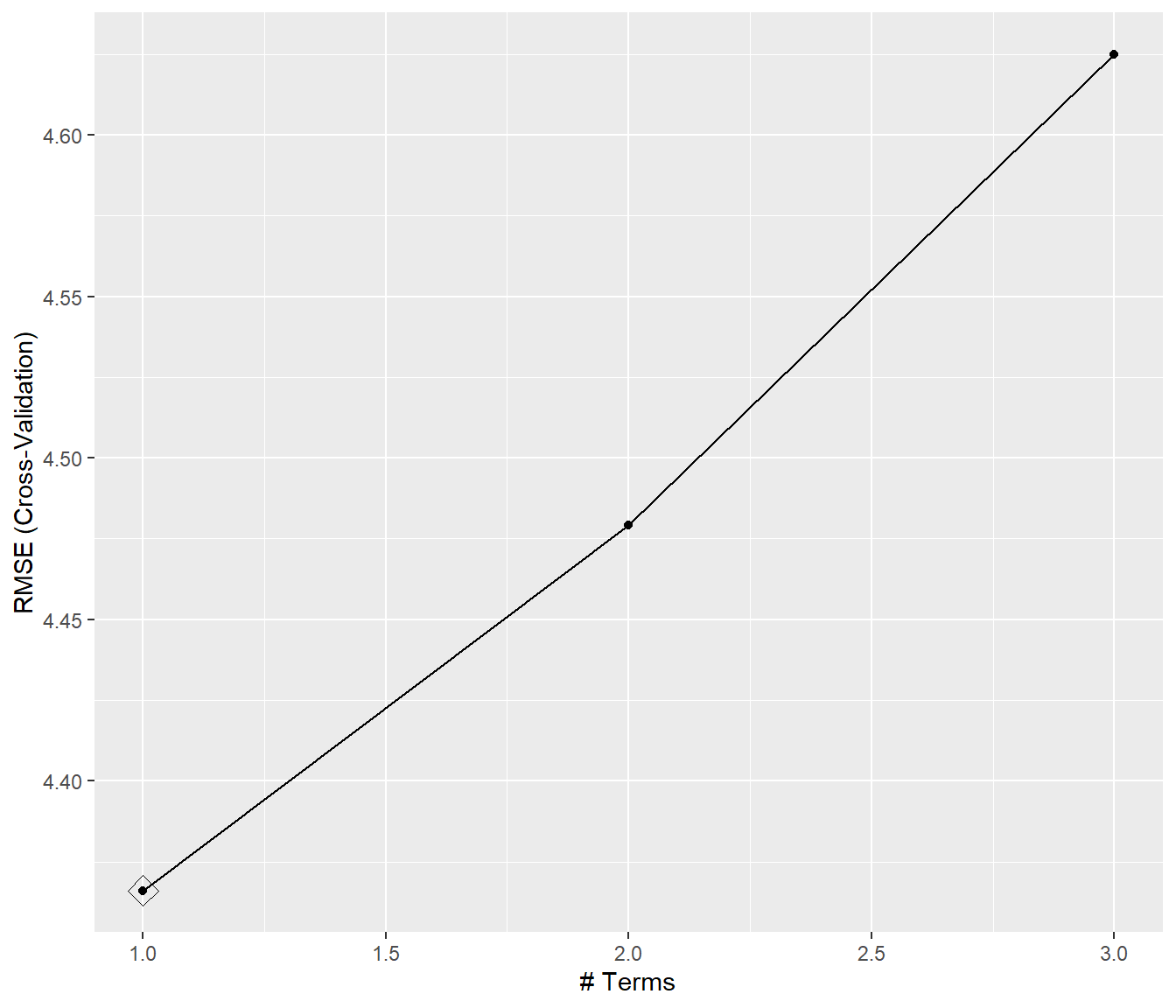

Figura 7.24: Errores RMSE de validación cruzada de los modelos PPR en función del numero de términos nterms, resaltando el valor óptimo.

Analizamos el modelo final ajustado (ver Figura 7.25):

summary(caret.ppr$finalModel)

## Call:
## ppr(x = as.matrix(x), y = y, nterms = param$nterms)
## 
## Goodness of fit:
##  1 terms 
## 4436.727 
## 
## Projection direction vectors ('alpha'):
##           vh         wind     humidity         temp          ibh          dpg 
## -0.016091543 -0.167891347  0.351773894  0.907301452 -0.001828865  0.026901492 
##          ibt          vis          doy 
##  0.148021198 -0.026470384 -0.035703896 
## 
## Coefficients of ridge terms ('beta'):
##   term 1 
## 6.853971

plot(caret.ppr$finalModel)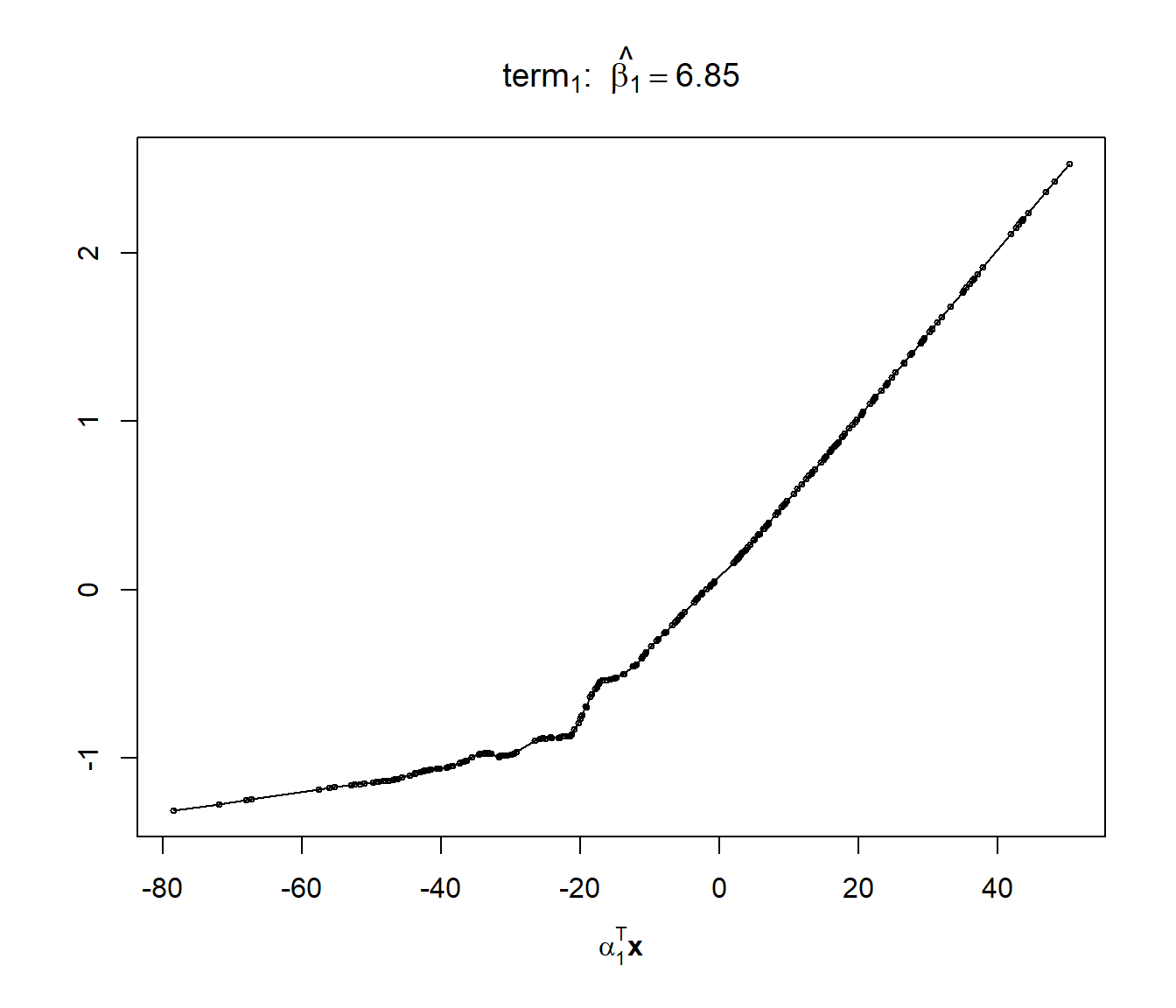

Figura 7.25: Estimación de la función ridge del ajuste PPR (con selección óptima del número de componentes).

# varImp(caret.ppr) # emplea una medida genérica de importancia
pred <- predict(caret.ppr, newdata = test)
accuracy(pred, obs)

##          me        rmse         mae         mpe        mape   r.squared 
##   0.3135877   3.3652891   2.7061615 -10.7532705  33.8333646   0.8249710

Para ajustar un modelo single index también se podría emplear la función npindex() del paquete np (que implementa el método de Ichimura, 1993, considerando un estimador local constante), aunque en este caso ni el tiempo de computación ni el resultado es satisfactorio⁵²:

library(np)
bw <- npindexbw(O3 ~ vh + wind + humidity + temp + ibh + dpg + ibt + vis + doy,
                data = train, optim.method = "BFGS", nmulti = 1) # Por defecto nmulti = 5
# summary(bw)

sindex <- npindex(bws = bw, gradients = TRUE)
summary(sindex)

## 
## Single Index Model
## Regression Data: 264 training points, in 9 variable(s)
## 
##       vh     wind humidity     temp       ibh      dpg      ibt        vis
## Beta:  1 4.338446 6.146688 10.44244 0.0926648 3.464211 5.017786 -0.5646063
##             doy
## Beta: -1.048745
## Bandwidth: 16.54751
## Kernel Regression Estimator: Local-Constant
## 
## Residual standard error: 3.520037
## R-squared: 0.806475
## 
## Continuous Kernel Type: Second-Order Gaussian
## No. Continuous Explanatory Vars.: 1

Al representar la función ridge se observa que aparentemente la ventana seleccionada produce un infrasuavizado (sobreajuste; ver Figura 7.26):

plot(bw)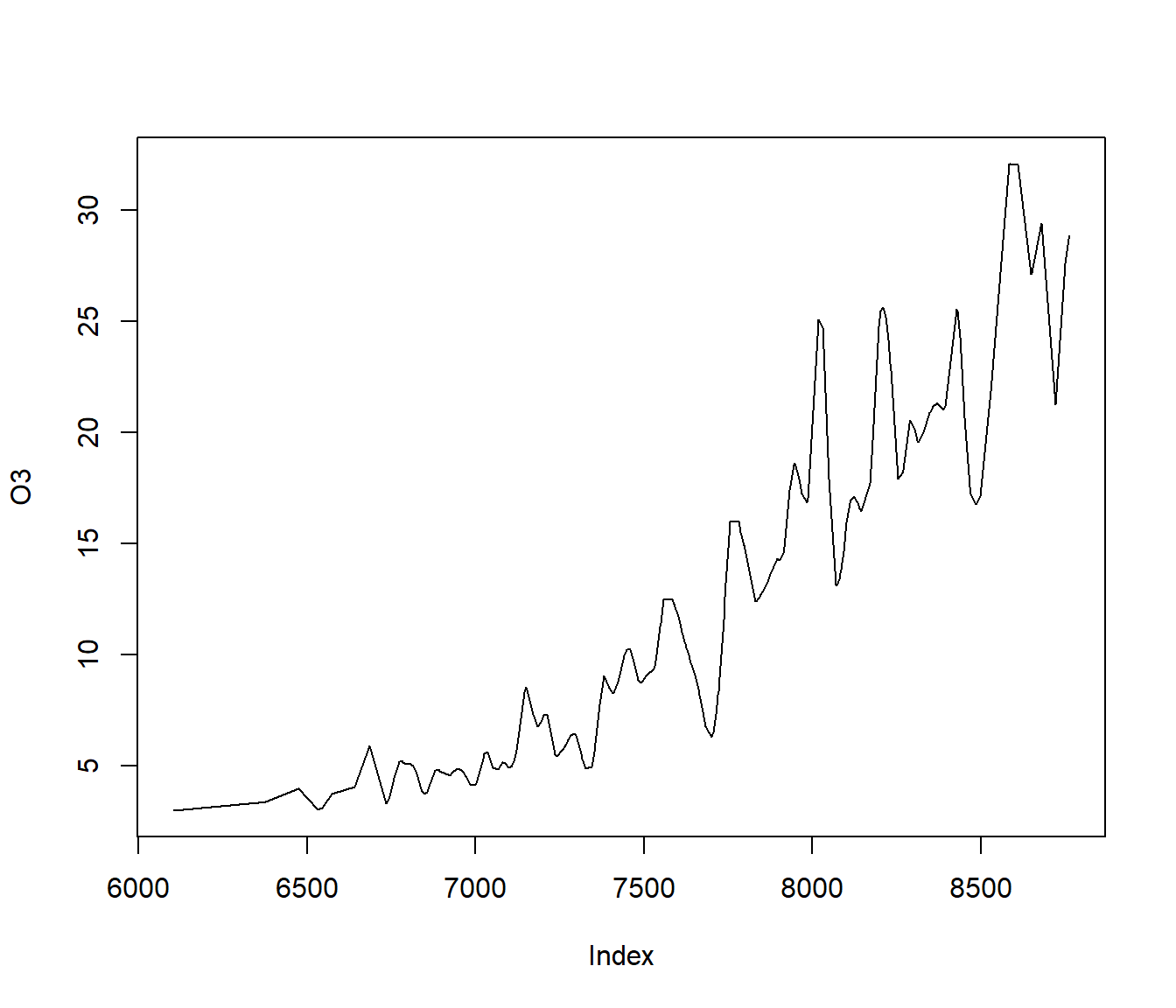

Figura 7.26: Estimación de la función ridge del modelo single index ajustado.

pred <- predict(sindex, newdata = test)
accuracy(pred, obs)

##          me        rmse         mae         mpe        mape   r.squared 
##   0.1712457   4.3725067   3.1789199 -10.2320531  35.2010284   0.7045213

References

Friedman, J. H., y Stuetzle, W. (1981). Projection pursuit regression. Journal of the American statistical Association, 76(376), 817-823. https://doi.org/10.1080/01621459.1981.10477729

Friedman, J. H., y Tukey, J. W. (1974). A projection pursuit algorithm for exploratory data analysis. IEEE Transactions on computers, 100(9), 881-890. https://doi.org/10.1109/t-c.1974.224051

Ichimura, H. (1993). Semiparametric least squares (SLS) and weighted SLS estimation of single-index models. Journal of Econometrics, 58(1), 71-120. https://doi.org/10.1016/0304-4076(93)90114-K

Kruskal, J. B. (1969). Toward a practical method which helps uncover the structure of a set of multivariate observations by finding the linear transformation which optimizes a new «index of condensation». Statistical Computation, 427-440. https://doi.org/10.1016/b978-0-12-498150-8.50024-0

Venables, W. N., y Ripley, B. D. (2002). Modern Applied Statistics with S. Springer New York. https://doi.org/10.1007/978-0-387-21706-2

Basada en la función ppreg() de S-PLUS e implementado en R por B.D. Ripley inicialmente para el paquete MASS.↩︎
No admite una fórmula del tipo respuesta ~ .:
```
bw <- npindexbw(O3 ~ ., data = train)
# Error in terms.formula(formula): '.' in formula and no 'data' argument
formula <- reformulate(setdiff(colnames(train), "O3"), response = "O3") # Escribe la formula explícitamente
```
El valor por defecto de nmulti = 5 (número de reinicios con punto de partida aleatorio del algoritmo de optimización) incrementa el tiempo de computación. Además, los resultados de texto contienen caracteres inválidos para compilar en LaTeX.↩︎