Capítulo 1 Introducción al aprendizaje estadístico
La denominada ciencia de datos (data science; también denominada science of learning) se ha vuelto muy popular hoy en día. Se trata de un campo multidisciplinar, con importantes aportaciones estadísticas e informáticas, dentro del que se incluyen disciplinas como minería de datos (data mining), aprendizaje automático (machine learning), aprendizaje profundo (deep learning), modelado predictivo (predictive modeling), extracción de conocimiento (knowlegde discovery) y también el aprendizaje estadístico (statistical learning, p. ej. Vapnik, 1998, 2000).
Podemos definir la ciencia de datos como el conjunto de conocimientos y herramientas utilizados en las distintas etapas del análisis de datos (ver Figura 1.1). Otras definiciones podrían ser:
El arte y la ciencia del análisis inteligente de los datos.
El conjunto de herramientas para entender y modelizar conjuntos (complejos) de datos.
El proceso de descubrir patrones y obtener conocimiento a partir de grandes conjuntos de datos (big data).
Además, esta ciencia incluye también la gestión (sin olvidarnos del proceso de obtención) y la manipulación de los datos.
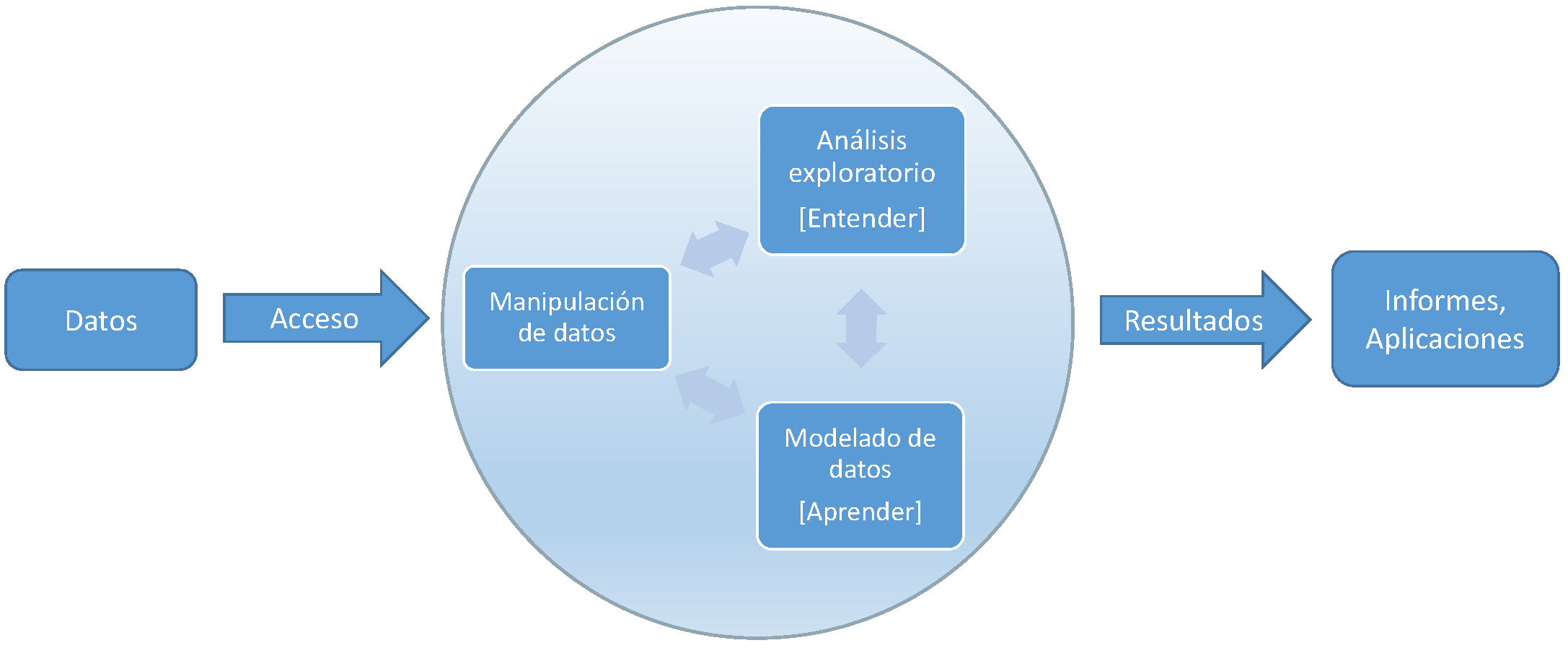
Figura 1.1: Etapas en el análisis de datos.
Una de estas etapas (que están interrelacionadas) es la construcción de modelos, a partir de los datos, para aprender y predecir. Podríamos decir que el aprendizaje estadístico (AE) se encarga de este problema desde un punto de vista estadístico.
En estadística se consideran modelos estocásticos (con componente aleatoria), para tratar de tener en cuenta la incertidumbre debida a que no se disponga de toda la información sobre las variables que influyen en el fenómeno de interés. Esto es lo que se conoce como aleatoriedad aparente:
“Nothing in Nature is random… a thing appears random only through the incompleteness of our knowledge.”
— Spinoza, Baruch (Ethics, 1677).
Aunque hoy en día gana peso la idea de la física cuántica de que en el fondo hay una aleatoriedad intrínseca:
“To my mind, although Spinoza lived and thought long before Darwin, Freud, Einstein, and the startling implications of quantum theory, he had a vision of truth beyond what is normally granted to human beings.”
— Shirley, Samuel (Complete Works, 2002). Traductor de la obra completa de Spinoza al inglés.
La inferencia estadística proporciona herramientas para ajustar este tipo de modelos a los datos observados (seleccionar un modelo adecuado, estimar sus parámetros y contrastar su validez). Sin embargo, en la aproximación estadística clásica, como primer objetivo se trata de explicar por completo lo que ocurre en la población y, suponiendo que esto se puede hacer con modelos tratables analíticamente, emplear resultados teóricos (típicamente resultados asintóticos) para realizar inferencias (entre ellas la predicción). Los avances en computación han permitido el uso de modelos estadísticos más avanzados, principalmente métodos no paramétricos, muchos de los cuales no pueden ser tratados analíticamente (o no por completo). Este es el campo de la estadística computacional4. Desde este punto de vista, el AE se enmarcaría en este campo.
Cuando pensamos en AE, pensamos en:
- Flexibilidad: se tratan de obtener las conclusiones basándose únicamente en los datos, evitando asumir hipótesis para poder emplear resultados teóricos. La idea es “dejar hablar” a los datos, no “encorsetarlos” a priori, dándoles mayor peso que a los modelos (power to the data es un manifiesto del ML/AE).
Procesamiento automático de datos: de forma que el proceso de aprendizaje pueda realizarse con la menor intervención interactiva por parte del analista.
Big data: en el sentido amplio. Además de tamaño muestral o número de características, “big” puede hacer referencia a datos complejos o con necesidad de alta velocidad de proceso.
Predicción: el objetivo (inicial) suele ser únicamente la predicción de nuevas observaciones, los métodos son simples algoritmos.
Por el contrario, muchos de los métodos del AE no se preocupan (o se preocupan poco) por:
Reproducibilidad o repetibilidad: pequeños cambios en los datos pueden producir cambios notables en el modelo ajustado, aunque no deberían influir mucho en las predicciones. Además, muchas de las técnicas son aleatorias y el resultado puede depender de la semilla empleada (principalmente del tamaño muestral).
Cuantificación de la incertidumbre (en términos de probabilidad): se obtienen medidas globales de la eficiencia del algoritmo, pero resulta complicado cuantificar la precisión de una predicción concreta (en principio no se pueden obtener intervalos de predicción).
Inferencia: aparte de la predicción, la mayoría de los métodos no permiten realizan inferencias sobre características de la población (como contrastes de hipótesis).
Además, esta aproximación puede presentar diversos inconvenientes:
Algunos métodos son poco interpretables (se sacrifica la interpretabilidad por la precisión de las predicciones). Algunos son auténticas “cajas negras” y resulta complicado conocer los detalles del proceso interno utilizado para obtener las predicciones, incluyendo las interacciones y los efectos de los distintos predictores. Esto puede ser un problema tan complejo como su ajuste. En la Sección 1.5 se comentan, muy por encima, algunas herramientas que pueden ayudar a hacerlo.
Pueden aparecer problemas de sobreajuste (overfitting). Muchos métodos son tan flexibles que pueden llegar a ajustar “demasiado bien” los datos, pero pueden ser poco eficientes para predecir nuevas observaciones. En la Sección 1.3 se describe con detalle este problema (y a continuación el procedimiento habitual para tratar de solventarlo). En los métodos estadísticos clásicos es más habitual que aparezcan problemas de infraajuste (underfitting).
Pueden presentar más problemas al extrapolar o interpolar (en comparación con los métodos clásicos). En general, se aplica el dicho solo viste donde estuviste. Cuanto más flexible sea el algoritmo, más cuidado habría que tener al predecir en nuevas observaciones alejadas de los valores de la muestra en la que se realizó el ajuste.
Bibliografía
Lauro (1996) definió la estadística computacional como la disciplina que tiene como objetivo “diseñar algoritmos para implementar métodos estadísticos en computadoras, incluidos los impensables antes de la era de las computadoras (por ejemplo, bootstrap, simulación), así como hacer frente a problemas analíticamente intratables”.↩︎