1.4 La maldición de la dimensionalidad
Podríamos pensar que al aumentar el número de variables explicativas se mejora la capacidad predictiva de los modelos. Lo cual, en general, sería cierto si realmente los predictores fuesen de utilidad para explicar la respuesta. Sin embargo, al aumentar el número de dimensiones se pueden agravar notablemente muchos de los problemas que ya pueden aparecer en dimensiones menores; esto es lo que se conoce como la maldición de la dimensionalidad (curse of dimensionality, Bellman, 1961).
Uno de estos problemas es el denominado efecto frontera que ya puede aparecer en una dimensión, especialmente al trabajar con modelos flexibles (como ajustes polinómicos con grados altos o los métodos locales que trataremos en el Capítulo 6). La idea es que en la “frontera” del rango de valores de una variable explicativa vamos a disponer de pocos datos y los errores de predicción van a tener gran variabilidad (se están haciendo extrapolaciones de los datos, más que interpolaciones, y van a ser menos fiables).
Cuando el número de datos es más o menos grande, podríamos pensar en predecir la respuesta a partir de lo que ocurre en las observaciones cercanas a la posición de predicción, esta es la idea de los métodos locales (Sección 7.1). Uno de los métodos de este tipo más conocidos es el de los k-vecinos más cercanos (k-nearest neighbors; KNN). Se trata de un método muy simple, pero que puede ser muy efectivo, que se basa en la idea de que localmente la media condicional (la predicción óptima) es constante. Concretamente, dados un entero \(k\) (hiperparámetro) y un conjunto de entrenamiento \(\mathcal{T}\), para obtener la predicción correspondiente a un vector de valores de las variables explicativas \(\mathbf{x}\), el método de regresión17 KNN promedia las observaciones en un vecindario \(\mathcal{N}_k(\mathbf{x}, \mathcal{T})\) formado por las \(k\) observaciones más cercanas a \(\mathbf{x}\): \[\hat{Y}(\mathbf{x}) = \hat{m}(\mathbf{x}) = \frac{1}{k} \sum_{i \in \mathcal{N}_k(\mathbf{x}, \mathcal{T})} Y_i\] Para ello sería necesario definir una distancia, normalmente la distancia euclídea entre los predictores estandarizados. Este método está implementado en numerosos paquetes, por ejemplo en la función knnreg() del paquete caret.
Como ejemplo consideraremos un problema de regresión simple, con un conjunto de datos simulados (del proceso ya considerado en la Sección 1.3.1) con 100 observaciones (que ya podríamos considerar que no es muy pequeño; ver Figura 1.15):
# Simulación datos
n <- 100
x <- seq(0, 1, length = n)
mu <- 2 + 4*(5*x - 1)*(4*x - 2)*(x - 0.8)^2 # grado 4
sd <- 0.5
set.seed(1)
y <- mu + rnorm(n, 0, sd)
datos <- data.frame(x = x, y = y)
# Representar
plot(x, y)
lines(x, mu, lwd = 2, col = "lightgray")
# Ajuste de los modelos
library(caret)
# k = número de observaciones más cercanas
fit1 <- knnreg(y ~ x, data = datos, k = 5) # 5% de los datos (n = 100)
fit2 <- knnreg(y ~ x, data = datos, k = 10)
fit3 <- knnreg(y ~ x, data = datos, k = 20)
# Añadir predicciones y leyenda
newdata <- data.frame(x = x)
lines(x, predict(fit1, newdata), lwd = 2, lty = 3)
lines(x, predict(fit2, newdata), lwd = 2, lty = 2)
lines(x, predict(fit3, newdata), lwd = 2)
legend("topright", legend = c("Verdadero", "5-NN", "10-NN", "20-NN"),
lty = c(1, 3, 2, 1), lwd = 2, col = c("lightgray", 1, 1, 1))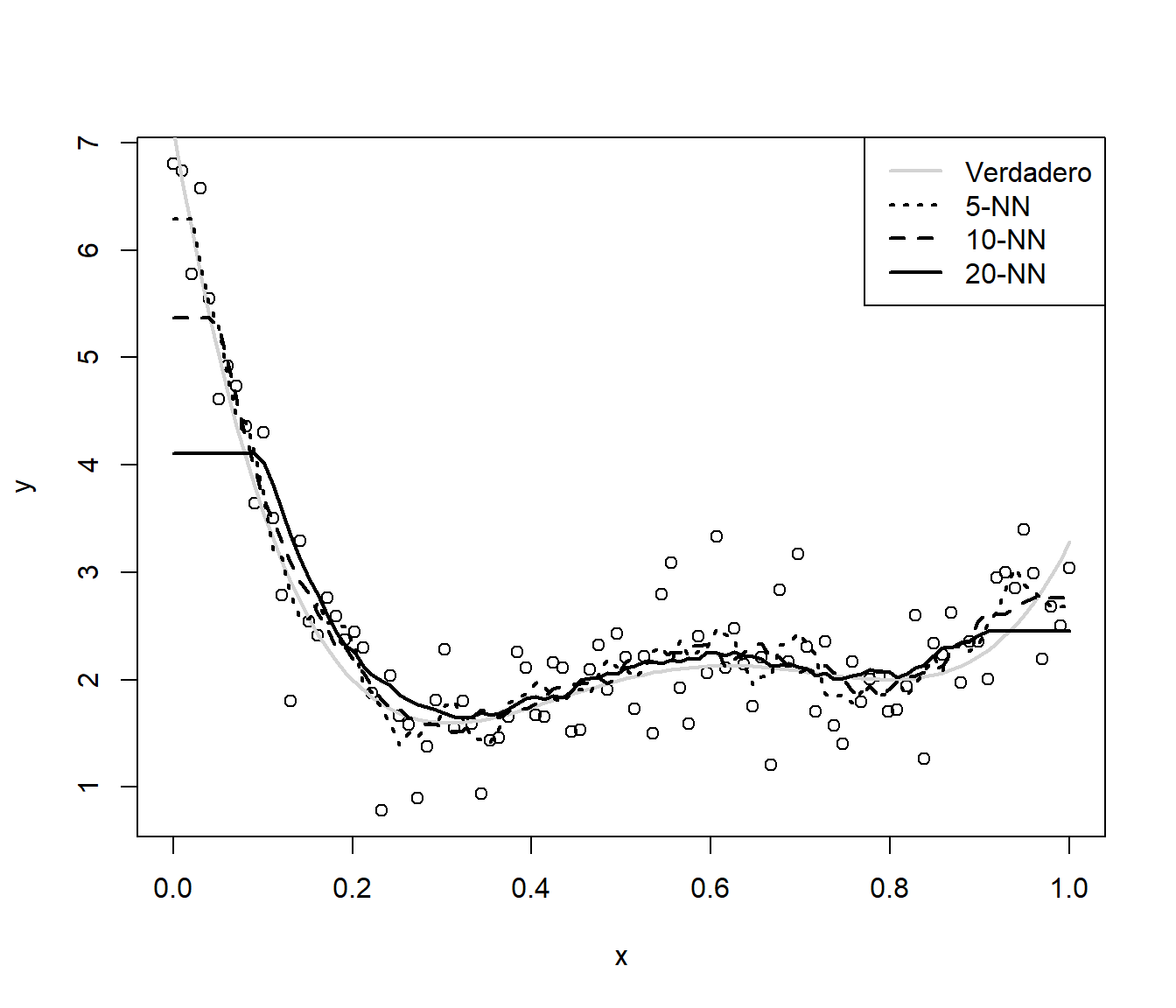
Figura 1.15: Predicciones con el método KNN y distintos vecindarios.
A medida que aumenta \(k\) disminuye la complejidad del modelo y se observa un incremento del efecto frontera. Habría que seleccionar un valor óptimo de \(k\) (buscando un equilibro entre sesgo y varianza, como se mostró en la Sección 1.3.1 y se ilustrará en la última sección de este capítulo empleando este método con el paquete caret), que dependerá de la tendencia teórica y del número de datos. En este caso, para \(k=5\), podríamos pensar que el efecto frontera aparece en el 10 % más externo del rango de la variable explicativa (con un número mayor de datos podría bajar al 1 %). Al aumentar el número de variables explicativas, considerando que el 10 % más externo del rango de cada una de ellas constituye la “frontera” de los datos, tendríamos que la proporción de frontera sería \(1-0.9^d\), siendo \(d\) el número de dimensiones. Lo que se traduce en que, con \(d = 10\), el 65 % del espacio predictivo sería frontera y en torno al 88 % para \(d=20\), es decir, al aumentar el número de dimensiones el problema del efecto frontera será generalizado (ver Figura 1.16).
curve(1 - 0.9^x, 0, 200, ylab = 'Proporción de frontera',
xlab = 'Número de dimensiones')
curve(1 - 0.95^x, lty = 2, add = TRUE)
curve(1 - 0.99^x, lty = 3, add = TRUE)
abline(h = 0.5, col = "lightgray")
legend("bottomright", title = "Rango en cada dimensión",
legend = c("10%" , "5%", "1%"), lty = c(1, 2, 3))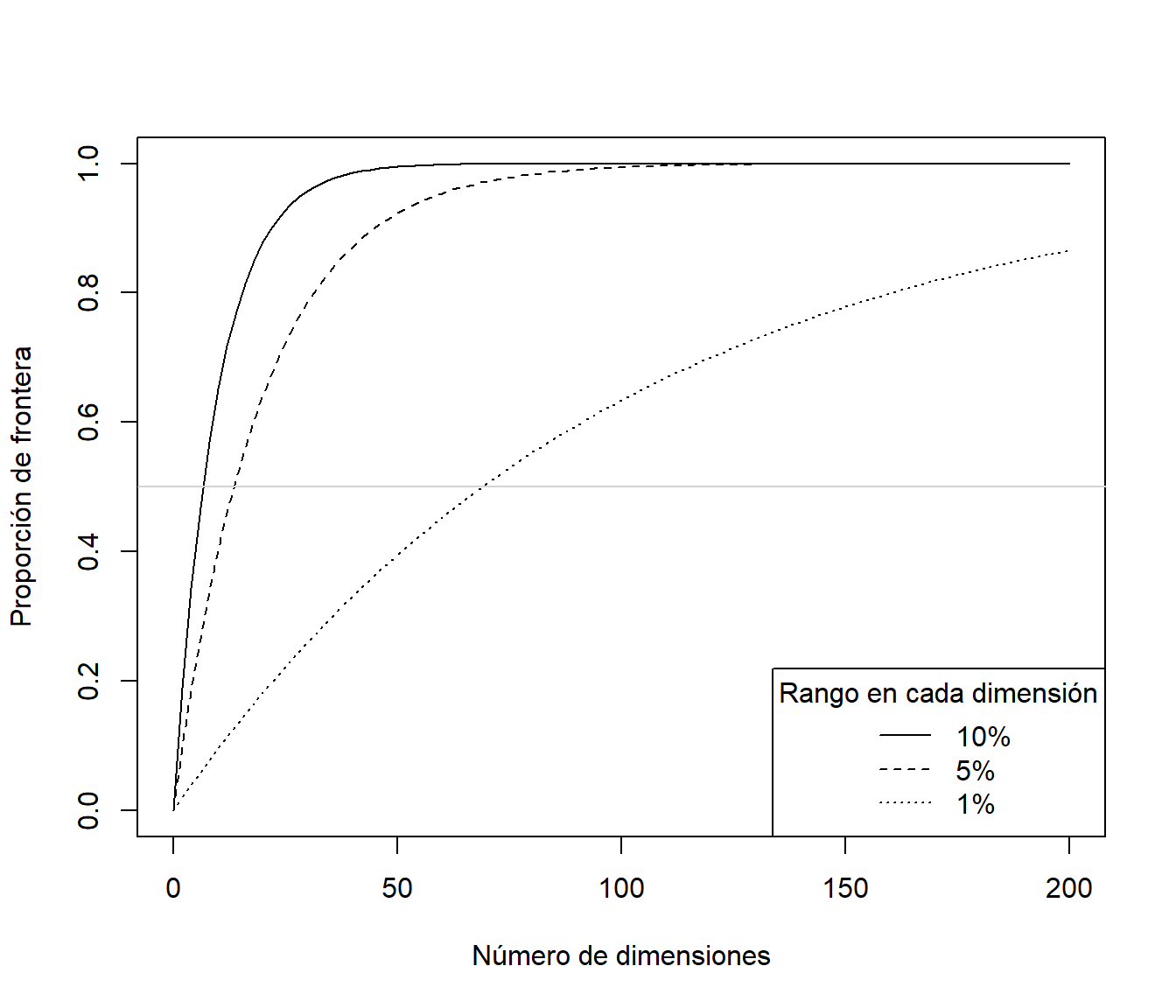
Figura 1.16: Proporción de frontera dependiendo del número de dimensiones y del porcentaje de valores considerados extremos en cada dimensión.
Desde otro punto de vista, suponiendo que los predictores se distribuyen de forma uniforme, la densidad de las observaciones es proporcional a \(n^{1/d}\), siendo \(n\) el tamaño muestral. Por lo que si consideramos que una muestra de tamaño \(n=100\) es suficientemente densa en una dimensión, para obtener la misma densidad muestral en 10 dimensiones tendríamos que disponer de un tamaño muestral de \(n = 100^{10} = 10^{20}\). Por tanto, cuando el número de dimensiones es grande no va a haber muchas observaciones en el entorno de la posición de predicción y puede haber serios problemas de sobreajuste si se pretende emplear un modelo demasiado flexible (por ejemplo, KNN con \(k\) pequeño). Hay que tener en cuenta que, en general, fijado el tamaño muestral, la flexibilidad de los modelos aumenta al aumentar el número de dimensiones del espacio predictivo.
Otro de los problemas que se agravan notablemente al aumentar el número de dimensiones es el de colinealidad (Sección 2.1.1), o en general el de concurvidad (Sección 7.3.3), que puede producir que muchos métodos (como los modelos lineales o las redes neuronales) sean muy poco eficientes o inestables (llegando incluso a que no se puedan aplicar). Además, complica notablemente la interpretación de cualquier método. Esto está relacionado también con la dificultad para determinar qué variables son de interés para predecir la respuesta (i. e. no son ruido). Debido a la aleatoriedad, predictores que realmente no están relacionados con la respuesta pueden ser tenidos en cuenta por el modelo con mayor facilidad (KNN con las opciones habituales tiene en cuenta todos los predictores con el mismo peso). Lo que resulta claro es que si se agrega ruido se producirá un incremento en el error de predicción. Incluso si las variables añadidas resultan ser relevantes, si el número de observaciones es pequeño en comparación, el incremento en la variabilidad de las predicciones puede no compensar la disminución del sesgo de predicción.
Como conclusión, en el caso multidimensional habrá que tratar de emplear métodos que minimicen estos problemas. Muchos métodos de AE realizan automáticamente una selección de predictores (o una ponderación, asignando más o menos peso según su relevancia), normalmente a través de un hiperparámetro de complejidad del modelo. Un ejemplo serían los arboles de decisión descritos en el Capítulo 3. En este caso, se habla de procedimientos integrados de selección (embedded selection methods). Sin embargo, el procedimiento habitual es emplear métodos por pasos que vayan añadiendo y/o eliminando predictores tratando de buscar la combinación óptima que maximice el rendimiento del modelo. Por ejemplo, en las secciones 2.1.2 y 2.2.1, se describen los procedimientos tradicionales de inferencia para modelos lineales y modelos lineales generalizados. En este tipo de métodos, que utilizan un algoritmo de búsqueda para seleccionar los predictores que se incluirán en el ajuste, se emplea un procedimiento de selección denominado envolvente (wrapper selection method). Una alternativa más simple, para evitar problemas computacionales, es el filtrado previo de los predictores (filter methods), de forma que solo se incluyen en el ajuste los que aparentemente están más relacionados con la respuesta. Sin embargo, hay que tener en cuenta que las medidas clásicas de dependencia, como el coeficiente de correlación de Pearson o el coeficiente de correlación parcial, solo permiten detectar relaciones simples entre predictores y respuesta. Puede ser preferible emplear medidas propuestas recientemente, como la correlación de distancias (Székely et al., 2007), que también permiten cuantificar relaciones no lineales de distintos tipos de predictores (univariantes, multivariantes, funcionales, direccionales…)18. La construcción y selección de predictores es una de las líneas tradicionales de estudio en AE/ML, aunque quedaría fuera de los objetivos principales de este libro y solo se tratará superficialmente. Para más detalles, ver por ejemplo Kuhn y Johnson (2019).
Bibliografía
En el caso de clasificación se considerarían las variables indicadoras de las categorías y se obtendrían las frecuencias relativas en el vecindario como estimaciones de las probabilidades de las clases.↩︎
Por ejemplo, Febrero-Bande et al. (2019) propusieron un método secuencial (hacia delante) que utiliza la correlación de distancias para seleccionar predictores, implementado en la función
fregre.gsam.vs()del paquetefda.usc(Febrero-Bande y Oviedo de la Fuente, 2012).↩︎