1.2 Métodos de aprendizaje estadístico
Dentro de los problemas que aborda el aprendizaje estadístico se suelen diferenciar dos grandes bloques: el aprendizaje no supervisado y el supervisado. El aprendizaje no supervisado comprende los métodos exploratorios, es decir, aquellos en los que no hay una variable respuesta (al menos no de forma explícita). El principal objetivo de estos métodos es entender las relaciones y estructuras presentes en los datos, y pueden clasificarse en las siguientes categorías:
Análisis descriptivo.
Métodos de reducción de la dimensión (análisis de componentes principales, análisis factorial…).
Métodos de agrupación (análisis clúster).
Detección de datos atípicos.
Es decir, los métodos descriptivos tradicionalmente incluidos en estadística multivariante (ver Everitt y Hothorn, 2011; Hair et al., 1998; o Härdle y Simar, 2013, por ejemplo, para una introducción a los métodos clásicos).
El aprendizaje supervisado engloba los métodos predictivos, en los que una de las variables está definida como variable respuesta. Su principal objetivo es la construcción de modelos que posteriormente se utilizarán, sobre todo, para hacer predicciones. Dependiendo del tipo de variable respuesta se diferencia entre:
Clasificación: si la respuesta es categórica (también se emplea la denominación de variable cualitativa, discreta o factor).
Regresión: cuando la respuesta es numérica (cuantitativa).
En este libro nos centraremos únicamente en el campo del aprendizaje supervisado y combinaremos la terminología propia de la estadística con la empleada en AE. Por ejemplo, en estadística es habitual considerar un problema de clasificación como un caso particular de regresión, empleando los denominados modelos de regresión generalizados (en la Sección 2.2 se introducen los modelos lineales generalizados, GLM). Por otra parte, en ocasiones se distingue entre casos particulares de un mismo tipo de modelos, como los considerados en el diseño de experimentos (ver Miller et al., 1973; o Lawson, 2014, por ejemplo).
1.2.1 Notación y terminología
Denotaremos por \(\mathbf{X}=(X_1, X_2, \ldots, X_p)\) al vector formado por las variables predictoras (variables explicativas o variables independientes; también inputs o features en la terminología de ML), cada una de las cuales podría ser tanto numérica como categórica6. En general (ver comentarios más adelante), emplearemos \(Y(\mathbf{X})\) para referirnos a la variable objetivo (variable respuesta o variable dependiente; también output o target en la terminología de ML) que, como ya se comentó, puede ser una variable numérica (regresión) o categórica (clasificación).
Supondremos que el objetivo principal es, a partir de una muestra: \[\left\{\left( y_{i}, x_{1i}, \ldots, x_{pi} \right) : i = 1, \ldots, n \right\}\] obtener (futuras) predicciones \(\hat Y(\mathbf{x})\) de la respuesta para \(\mathbf{X}=\mathbf{x}=\left(x_{1}, \ldots, x_{p}\right)\).
En regresión consideraremos como base el siguiente modelo general (podría ser después de una transformación de la respuesta): \[\begin{equation} Y(\mathbf{X})=m(\mathbf{X})+\varepsilon \tag{1.1} \end{equation}\] donde \(m(\mathbf{x}) = E\left( \left. Y\right\vert \mathbf{X}=\mathbf{x} \right)\) es la media condicional, denominada función de regresión (o tendencia), y \(\varepsilon\) es un error aleatorio de media cero y varianza \(\sigma^2\), independiente de \(\mathbf{X}\). Este modelo puede generalizarse de diversas formas, por ejemplo, asumiendo que la distribución del error depende de \(\mathbf{X}\) (considerando \(\varepsilon(\mathbf{X})\) en lugar de \(\varepsilon\)) podríamos incluir dependencia y heterocedasticidad. En estos casos normalmente se supone que lo hace únicamente a través de la varianza (error heterocedástico independiente), denotando por \(\sigma^2(\mathbf{x}) = Var\left( \left. Y \right\vert \mathbf{X}=\mathbf{x} \right)\) la varianza condicional7.
Como ya se comentó, se podría considerar clasificación como un caso particular. Por ejemplo, definiendo \(Y(\mathbf{X})\) de forma que tome los valores \(1, 2, \ldots, K\), etiquetas que identifican las \(K\) posibles categorías (también se habla de modalidades, niveles, clases o grupos). Sin embargo, muchos métodos de clasificación emplean variables auxiliares (variables dummy), indicadoras de las distintas categorías, y emplearemos la notación anterior para referirnos a estas variables (también denominadas variables target). En cuyo caso, denotaremos por \(G(\mathbf{X})\) la respuesta categórica (la clase verdadera; \(g_i\), \(i =1, \ldots, n\), serían los valores observados) y por \(\hat G(\mathbf{X})\) el predictor.
Por ejemplo, en el caso de dos categorías, se suele definir \(Y\) de forma que toma el valor 1 en la categoría de interés (también denominada éxito o resultado positivo) y 0 en caso contrario (fracaso o resultado negativo)8. Además, en este caso, los modelos típicamente devuelven estimaciones de la probabilidad de la clase de interés en lugar de predecir directamente la clase, por lo que se empleará \(\hat p\) en lugar de \(\hat Y\). A partir de esa estimación se obtiene una predicción de la categoría. Normalmente se predice la clase más probable, lo que se conoce como la regla de Bayes, i. e. “éxito” si \(\hat p(\mathbf{x}) > c = 0.5\) y “fracaso” en caso contrario (con probabilidad estimada \(1 - \hat p(\mathbf{x})\)).
Es evidente que el modelo base general (1.1) puede no ser adecuado para modelar variables indicadoras (o probabilidades). Muchos de los métodos de AE emplean (1.1) para una variable auxiliar numérica (denominada puntuación o score) que se transforma a escala de probabilidades mediante la función logística (denominada función sigmoidal, sigmoid function, en ML)9: \[\operatorname{sigmoid}(s) = \frac{e^s}{1 + e^s}= \frac{1}{1 + e^{-s}}\] de forma que \(\hat p(\mathbf{x}) = \operatorname{sigmoid}(\hat Y(\mathbf{x}))\). Recíprocamente, empleando su inversa, la función logit: \[\operatorname{logit}(p)=\log\left( \frac{p}{1-p} \right)\] se pueden transformar las probabilidades a la escala de puntuaciones (ver Figura 1.2).
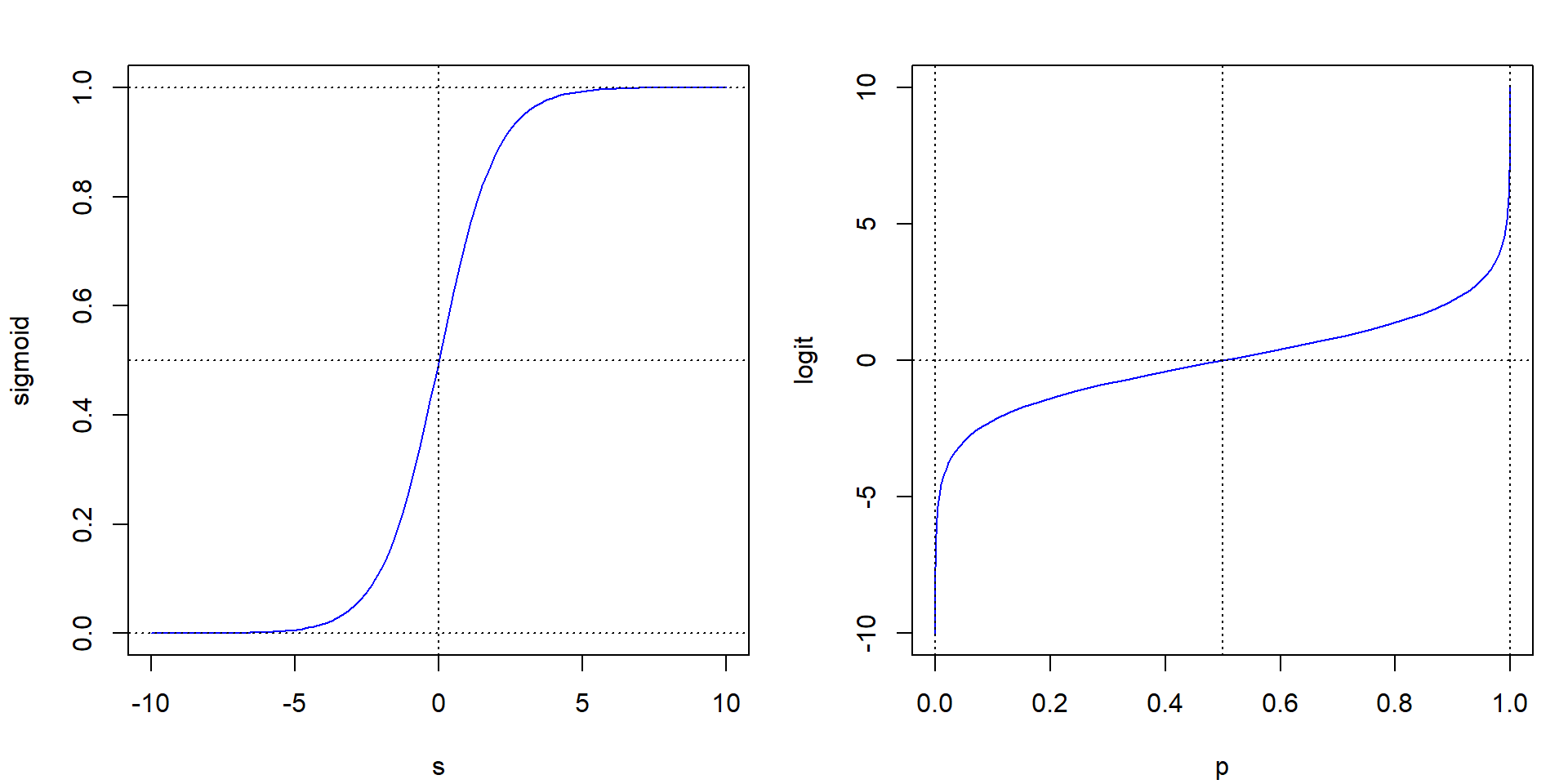
Figura 1.2: Funciones sigmoidal (izquierda) y logit (derecha).
Se puede generalizar el enfoque anterior para el caso de múltiples categorías. Por ejemplo, considerando variables indicadoras de cada categoría \(Y_1, \ldots, Y_K\) (en cada una de ellas se asigna al resto de categorías un resultado negativo), lo que se conoce como la estrategia de “uno contra todos” (One-vs-Rest, OVR). En este caso típicamente se emplea la función softmax para reescalar las puntuaciones a un conjunto válido de probabilidades: \[\hat p_k(\mathbf{x}) = \operatorname{softmax}_k(\hat Y_1(\mathbf{x}), \ldots, \hat Y_K(\mathbf{x}))\] para \(k = 1,\ldots, K\), siendo: \[\operatorname{softmax}_k(\mathbf{s}) = \frac{e^{s_k}}{\sum_{j=1}^K e^{s_j}}\] A partir de las cuales se obtiene la predicción de la categoría: \[\hat G(\mathbf{X}) = \underset{k}{\operatorname{argmax}} \left\{ \hat p_k(\mathbf{x}) : k = 1, 2, \ldots, K \right\}\]
Otra posible estrategia es la denominada “uno contra uno” (One-vs-One, OVO) o también conocida por “votación mayoritaria” (majority voting), que requiere entrenar un clasificador para cada par de categorías (se consideran \(K(K-1)/2\) subproblemas de clasificación binaria). En este caso se suele seleccionar como predicción la categoría que recibe más votos (la que resultó seleccionada por el mayor número de los clasificadores binarios).
Otros métodos (como por ejemplo los árboles de decisión, que se tratarán en el Capítulo 3) permiten la estimación directa de las probabilidades de cada clase.
1.2.2 Métodos (de aprendizaje supervisado) y paquetes de R
Hay una gran cantidad de métodos de aprendizaje supervisado implementados en centenares de paquetes de R (ver por ejemplo CRAN Task View: Machine Learning & Statistical Learning). A continuación se muestran los principales métodos y algunos de los paquetes de R que los implementan (muchos son válidos tanto para regresión como para clasificación, como por ejemplo los basados en árboles, aunque aquí aparecen en su aplicación habitual).
Métodos (principalmente) de clasificación:
Análisis discriminante (lineal, cuadrático), regresión logística, multinomial…:
stats,MASS.Árboles de decisión, bagging, bosques aleatorios, boosting:
rpart,party,C50,Cubist,randomForest,adabag,xgboost.Máquinas de soporte vectorial:
kernlab,e1071.
Métodos (principalmente) de regresión:
Modelos lineales:
Regresión lineal:
lm(),lme(),biglm.Regresión lineal robusta:
MASS::rlm().Métodos de regularización (ridge regression, LASSO):
glmnet,elasticnet.
Modelos lineales generalizados:
glm(),bigglm.Modelos paramétricos no lineales:
nls(),nlme.Regresión local (vecinos más próximos y métodos de suavizado):
kknn,loess(),KernSmooth,sm,np.Modelos aditivos generalizados:
mgcv,gam.Regresión spline adaptativa multivariante:
earth.Regresión por projection pursuit (incluyendo Single index model):
ppr(),np::npindex().Redes neuronales:
nnet,neuralnet.
Como todos estos paquetes emplean opciones, estructuras y convenciones sintácticas diferentes, se han desarrollado paquetes que proporcionan interfaces unificadas a muchas de estas implementaciones. Entre ellos podríamos citar caret (Kuhn, 2023; ver también Kuhn y Johnson, 2013), mlr3 (Bischl et al., 2024; Lang et al., 2019) y tidymodels (Kuhn y Silge, 2022; Kuhn y Wickham, 2020, 2023). En la Sección 1.6 se incluye una breve introducción al paquete caret que será empleado en diversas ocasiones a lo largo del presente libro.
También existen paquetes de R que permiten utilizar plataformas de ML externas, como por ejemplo h2o (LeDell y Poirier, 2020) o RWeka (Hornik et al., 2009). Adicionalmente, hay paquetes de R que disponen de entornos gráficos que permiten emplear estos métodos evitando el uso de comandos. Entre ellos estarían rattle (Williams, 2022; ver también Williams, 2011), radiant (Nijs, 2023) y Rcmdr (R-Commander, Fox et al., 2024) con el plugin RcmdrPlugin.FactoMineR (Husson et al., 2023).
Bibliografía
Aunque hay que tener en cuenta que algunos métodos están diseñados solo para predictores numéricos, otros solo para categóricos y algunos para ambos tipos.↩︎
Por ejemplo, considerando en el modelo base \(\sigma(\mathbf{X})\varepsilon\) como término de error y suponiendo adicionalmente que \(\varepsilon\) tiene varianza uno.↩︎
Otra alternativa sería emplear \(1\) y \(-1\), algo que simplifica las expresiones de algunos métodos.↩︎
De especial interés en regresión logística y en redes neuronales artificiales.↩︎