7.2 Splines
Un enfoque alternativo a los métodos de regresión local de la sección anterior consiste en trocear los datos en intervalos: se fijan unos puntos de corte \(z_i\), denominados nudos (knots), con \(i = 1, \ldots, k\), y se ajusta un polinomio en cada segmento, lo que se conoce como regresión segmentada (piecewise regression; ver Figura 7.5).
Un inconveniente de este método es que da lugar a discontinuidades en los puntos de corte, aunque pueden añadirse restricciones adicionales de continuidad (o incluso de diferenciabilidad) para evitarlo (p. ej. paquete segmented, Fasola et al., 2018).
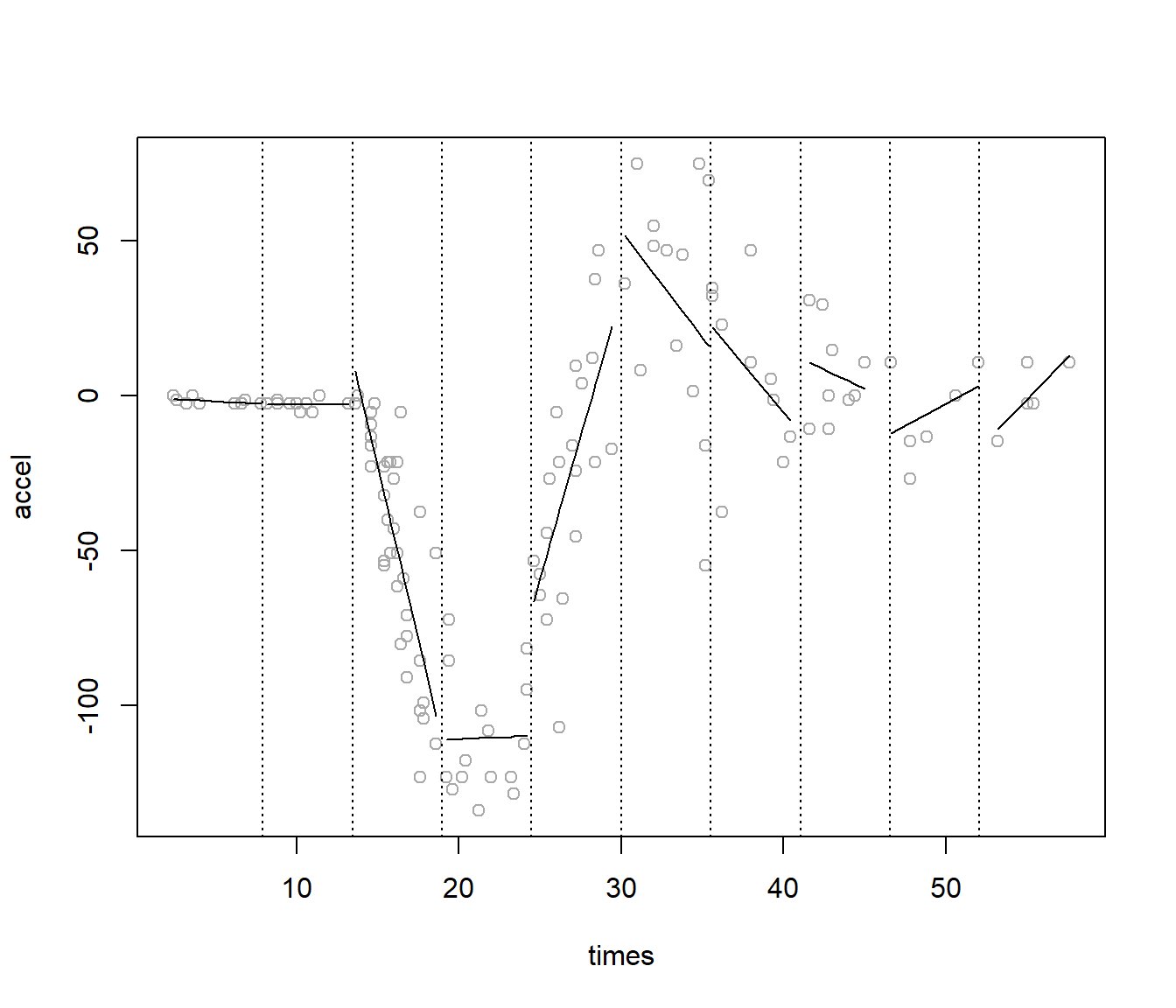
Figura 7.5: Estimación mediante regresión segmentada.
7.2.1 Splines de regresión
Cuando en cada intervalo se ajustan polinomios de orden \(d\) y se incluyen restricciones de forma que las derivadas sean continuas hasta el orden \(d-1\), se obtienen los denominados splines de regresión (regression splines). Puede verse que este tipo de ajustes equivalen a transformar la variable predictora \(X\), considerando por ejemplo la base de potencias truncadas (truncated power basis): \[1, x, \ldots, x^d, (x-z_1)_+^d,\ldots,(x-z_k)_+^d\] siendo \((x - z)_+ = \max(0, x - z)\), y posteriormente realizar un ajuste lineal: \[m(x) = \beta_0 + \beta_1 b_1(x) + \beta_2 b_2(x) + \ldots + \beta_{k+d} b_{k+d}(x)\]
Típicamente se seleccionan polinomios de grado \(d=3\), lo que se conoce como splines cúbicos, y nodos equiespaciados.
Además, se podrían emplear otras bases equivalentes.
Por ejemplo, para evitar posibles problemas computacionales con la base anterior, se suele emplear la denominada base \(B\)-spline (De Boor y De Boor, 1978), implementada en la función bs() del paquete splines (ver Figura 7.6):
nknots <- 9 # nodos internos; 10 intervalos
knots <- seq(min(times), max(times), len = nknots + 2)[-c(1, nknots + 2)]
library(splines)
fit1 <- lm(accel ~ bs(times, knots = knots, degree = 1))
fit2 <- lm(accel ~ bs(times, knots = knots, degree = 2))
fit3 <- lm(accel ~ bs(times, knots = knots)) # degree = 3
# Representar
plot(times, accel, col = 'darkgray')
newx <- seq(min(times), max(times), len = 200)
newdata <- data.frame(times = newx)
lines(newx, predict(fit1, newdata), lty = 3)
lines(newx, predict(fit2, newdata), lty = 2)
lines(newx, predict(fit3, newdata))
abline(v = knots, lty = 3, col = 'darkgray')
leyenda <- c("d=1 (df=11)", "d=2 (df=12)", "d=3 (df=13)")
legend("topright", legend = leyenda, lty = c(3, 2, 1))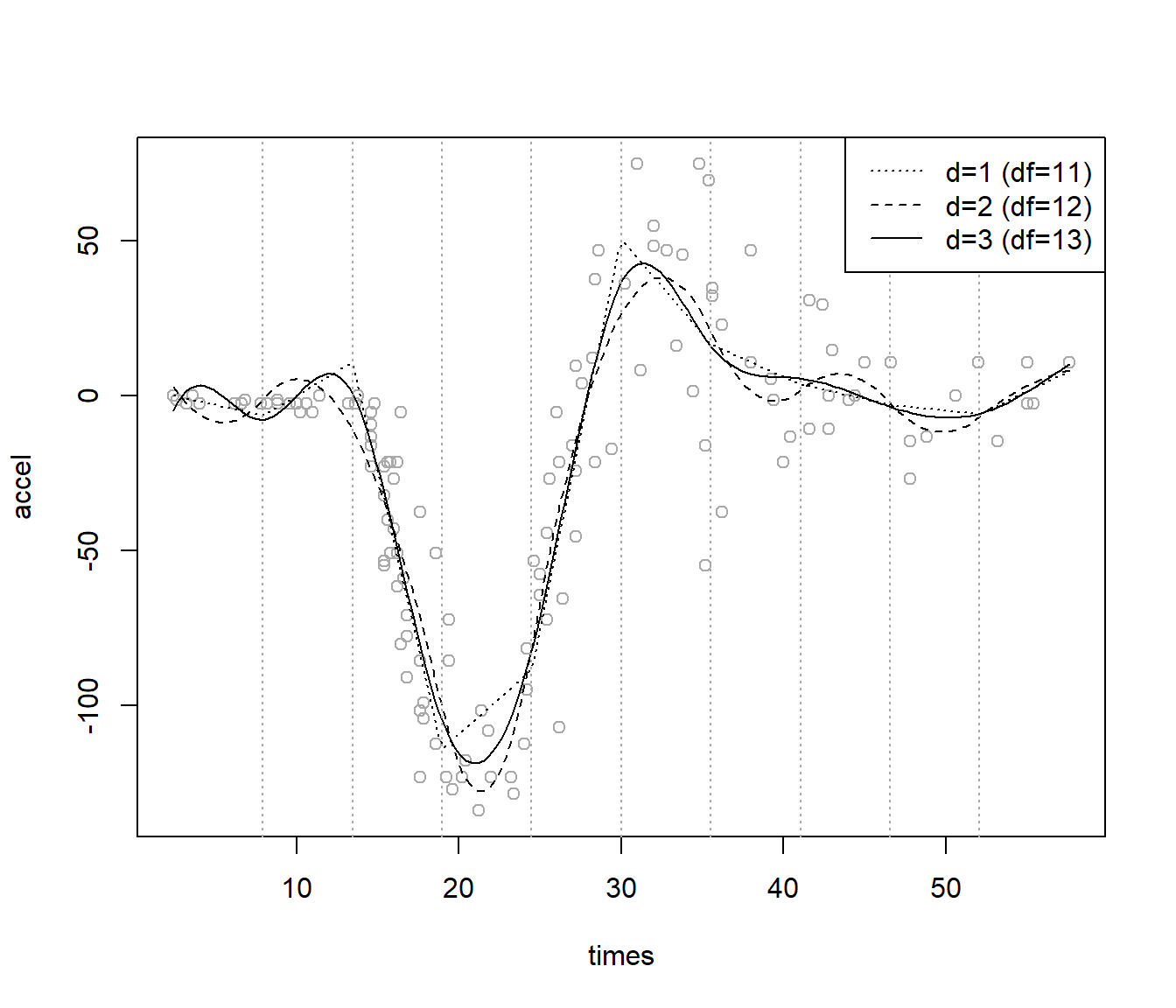
Figura 7.6: Ajustes mediante splines de regresión (de grados 1, 2 y 3).
El grado del polinomio y, sobre todo, el número de nodos, determinarán la flexibilidad del modelo.
El número de parámetros, \(k+d+1\), en el ajuste lineal (los grados de libertad) se puede utilizar como una medida de la complejidad (en la función bs() se puede especificar df en lugar de knots, y estos se generarán a partir de los cuantiles).
Como se comentó previamente, al aumentar el grado de un modelo polinómico se incrementa la variabilidad de las predicciones, especialmente en la frontera.
Para tratar de evitar este problema se suelen emplear los splines naturales, que son splines de regresión con restricciones adicionales de forma que el ajuste sea lineal en los intervalos extremos, lo que en general produce estimaciones más estables en la frontera y mejores extrapolaciones.
Estas restricciones reducen la complejidad (los grados de libertad del modelo), y al igual que en el caso de considerar únicamente las restricciones de continuidad y diferenciabilidad, resultan equivalentes a considerar una nueva base en un ajuste sin restricciones.
Por ejemplo, se puede emplear la función splines::ns() para ajustar un spline natural (cúbico por defecto; ver Figura 7.7):
plot(times, accel, col = 'darkgray')
fit4 <- lm(accel ~ ns(times, knots = knots))
lines(newx, predict(fit4, newdata))
lines(newx, predict(fit3, newdata), lty = 2)
abline(v = knots, lty = 3, col = 'darkgray')
leyenda <- c("ns (d=3, df=11)", "bs (d=3, df=13)")
legend("topright", legend = leyenda, lty = c(1, 2))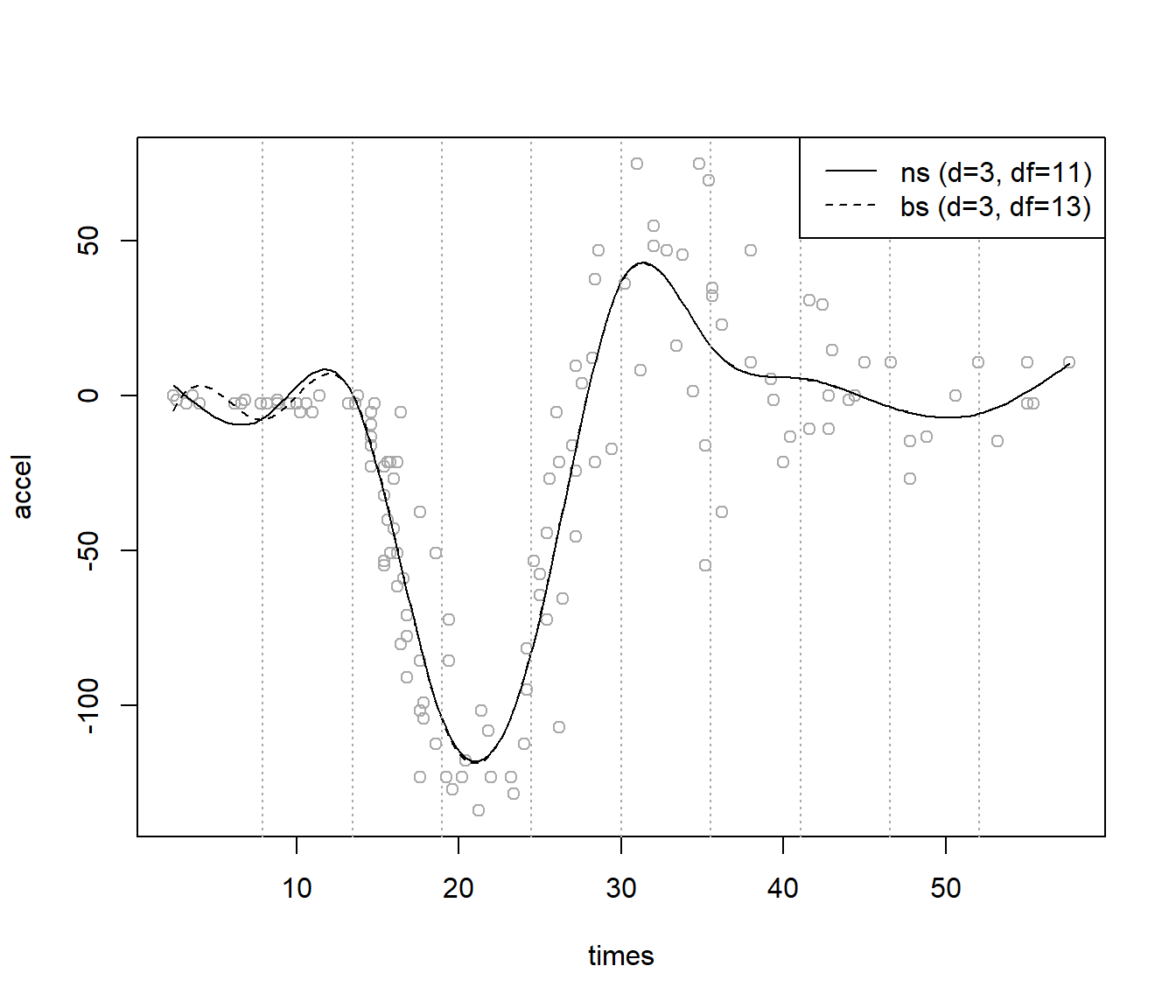
Figura 7.7: Ajuste mediante splines naturales (ns) y \(B\)-splines (bs).
La dificultad principal es la selección de los nodos \(z_i\). Si se consideran equiespaciados (o se emplea otro criterio, como los cuantiles), se puede seleccionar su número (equivalentemente, los grados de libertad) empleando validación cruzada. Sin embargo, es preferible utilizar más nodos donde aparentemente hay más variaciones en la función de regresión, y menos donde es más estable; esta es la idea de la regresión spline adaptativa, descrita en la Sección 7.4. Otra alternativa son los splines penalizados, descritos al final de esta sección.
7.2.2 Splines de suavizado
Los splines de suavizado (smoothing splines) se obtienen como la función \(s(x)\) suave (dos veces diferenciable) que minimiza la suma de cuadrados residual más una penalización que mide su rugosidad: \[\sum_{i=1}^{n} (y_i - s(x_i))^2 + \lambda \int s^{\prime\prime}(x)^2 dx\] siendo \(0 \leq \lambda < \infty\) el hiperparámetro de suavizado.
Puede verse que la solución a este problema, en el caso univariante, es un spline natural cúbico con nodos en \(x_1, \ldots, x_n\) y restricciones en los coeficientes determinadas por el valor de \(\lambda\) (es una versión regularizada de un spline natural cúbico). Por ejemplo, si \(\lambda = 0\) se interpolarán las observaciones, y cuando \(\lambda \rightarrow \infty\) el ajuste tenderá a una recta (con segunda derivada nula). En el caso multivariante, \(p> 1\), la solución da lugar a los denominados thin plate splines64.
Al igual que en el caso de la regresión polinómica local (Sección 7.1.2), estos métodos son suavizadores lineales: \[\hat{\mathbf{Y}} = S_{\lambda}\mathbf{Y}\] y para seleccionar el parámetro de suavizado \(\lambda\) podemos emplear los criterios de validación cruzada (dejando uno fuera), minimizando: \[CV(\lambda)=\frac{1}{n}\sum_{i=1}^n\left(\frac{y_i-\hat{s}_{\lambda}(x_i)}{1 - \{ S_{\lambda}\}_{ii}}\right)^2\] siendo \(\{ S_{\lambda}\}_{ii}\) el elemento \(i\)-ésimo de la diagonal de la matriz de suavizado; o validación cruzada generalizada (GCV), minimizando: \[GCV(\lambda)=\frac{1}{n}\sum_{i=1}^n\left(\frac{y_i-\hat{s}_{\lambda}(x_i)}{1 - \frac{1}{n}tr(S_{\lambda})}\right)^2\]
Análogamente, el número efectivo de parámetros o grados de libertad65 \(df_{\lambda}=tr(S_{\lambda})\) sería una medida de la complejidad del modelo equivalente a \(\lambda\) (muchas implementaciones permiten seleccionar la complejidad empleando \(df\)).
Este método de suavizado está implementado en la función smooth.spline() del paquete base.
Por defecto emplea GCV para seleccionar el parámetro de suavizado, aunque también admite CV y se puede especificar lambda o df (ver Figura 7.8).
Además de predicciones, el correspondiente método predict() también permite obtener estimaciones de las derivadas.
sspline.gcv <- smooth.spline(times, accel)
sspline.cv <- smooth.spline(times, accel, cv = TRUE)
plot(times, accel, col = 'darkgray')
lines(sspline.gcv)
lines(sspline.cv, lty = 2)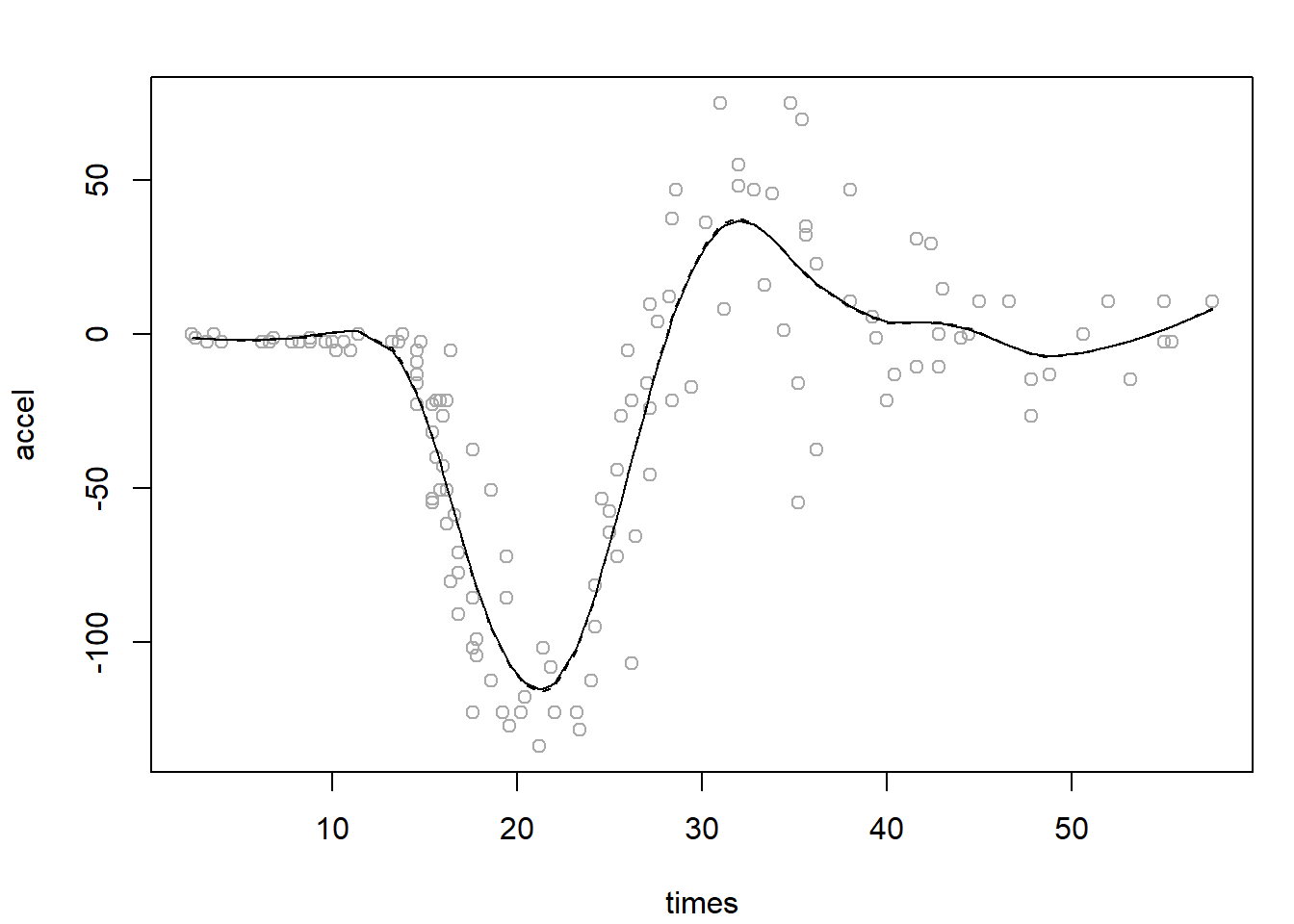
Figura 7.8: Ajuste mediante splines de suavizado, empleando GCV (línea contínua) y CV (línea discontínua) para seleccionar el parámetro de suavizado.
Cuando el número de observaciones es muy grande, y por tanto el número de nodos, pueden aparecer problemas computacionales al emplear estos métodos.
7.2.3 Splines penalizados
Los splines penalizados (penalized splines) combinan las dos aproximaciones anteriores. Incluyen una penalización que depende de la base considerada, y el número de nodos puede ser mucho menor que el número de observaciones (son un tipo de low-rank smoothers). De esta forma, se obtienen modelos spline con mejores propiedades, con un menor efecto frontera y en los que se evitan problemas en la selección de los nodos. Entre los más utilizados se encuentran los \(P\)-splines (Eilers y Marx, 1996), que emplean una base \(B\)-spline con una penalización simple basada en los cuadrados de diferencias de coeficientes consecutivos \((\beta_{i+1} - \beta_i)^2\).
Asimismo, un modelo spline penalizado se puede representar como un modelo lineal mixto, lo que permite emplear herramientas desarrolladas para este tipo de modelos; por ejemplo, las implementadas en el paquete nlme (Pinheiro et al., 2023), del que depende mgcv (Wood, 2017), que por defecto emplea splines penalizados.
Para más detalles, se recomiendan las secciones 5.2 y 5.3 de Wood (2017).