5.1 Clasificadores de máximo margen

Los clasificadores de máximo margen (maximal margin classifiers; también denominados hard margin classifiers) son un método de clasificación binaria que se utiliza cuando hay una frontera lineal que separa perfectamente los datos de entrenamiento de una categoría de los de la otra. Por conveniencia, etiquetamos las dos categorías como \(+1/-1\), es decir, los valores de la variable respuesta \(Y \in \{-1, 1\}\). Y suponemos que existe un hiperplano \[ \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \ldots + \beta_p X_p = 0,\] donde \(p\) es el número de variables predictoras, que tiene la propiedad de separar los datos de entrenamiento según la categoría a la que pertenecen, es decir, \[ y_i(\beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + \ldots + \beta_p x_{pi}) > 0\] para todo \(i = 1, 2, \ldots, n\), siendo \(n\) el número de datos de entrenamiento.

Una vez tenemos el hiperplano, clasificar una nueva observación \(\mathbf{x}\) se reduce a calcular el signo de \[m(\mathbf{x}) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_p x_p\] Si el signo es positivo, la observación se clasifica como perteneciente a la categoría \(+1\), y si es negativo a la categoría \(-1\). Además, el valor absoluto de \(m(\mathbf{x})\) nos da una idea de la distancia entre la observación y la frontera que define el hiperplano. En concreto \[\frac{y_i}{\sqrt {\sum_{j=1}^p \beta_j^2}}(\beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + \ldots + \beta_p x_{pi})\] sería la distancia de la observación \(i\)-ésima al hiperplano. Por supuesto, aunque clasifique los datos de entrenamiento sin error, no hay ninguna garantía de que clasifique bien nuevas observaciones, por ejemplo los datos de test. De hecho, si \(p\) es grande, es fácil que haya un sobreajuste.

En realidad, si existe al menos un hiperplano que separa perfectamente los datos de entrenamiento de las dos categorías, entonces va a haber infinitos. El objetivo es seleccionar un hiperplano que separe los datos lo mejor posible, en el sentido que exponemos a continuación. Dado un hiperplano de separación, se calculan sus distancias a todos los datos de entrenamiento y se define el margen como la menor de esas distancias. El método maximal margin classifier lo que hace es seleccionar, de entre los infinitos hiperplanos, aquel que tiene el mayor margen. Fijémonos en que siempre va a haber varias observaciones que equidistan del hiperplano de máximo margen, y cuya distancia es precisamente el margen. Esas observaciones reciben el nombre de vectores soporte (podemos obtener el hiperplano a partir de ellas) y son las que dan nombre a esta metodología (ver Figura 5.1).

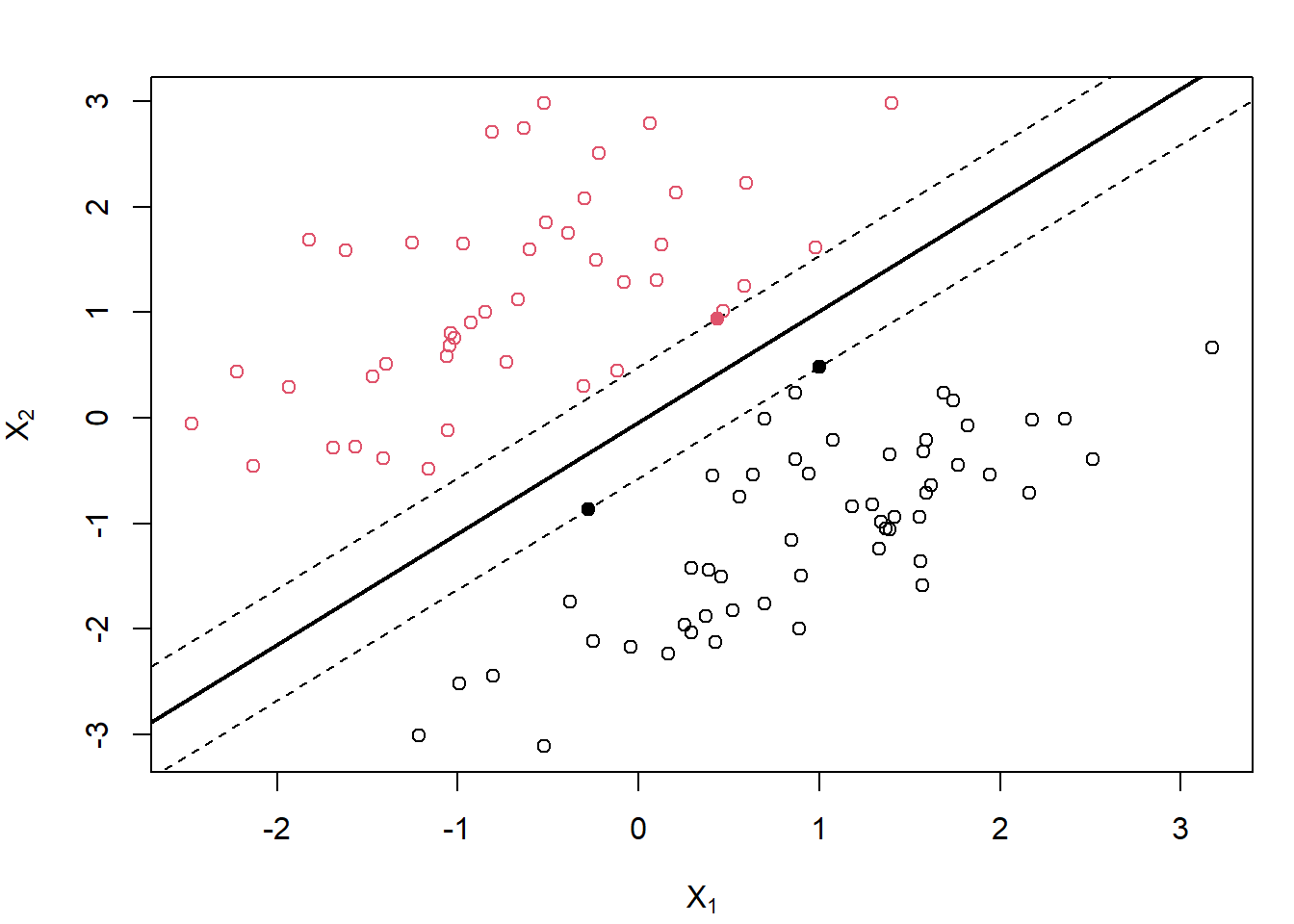
Figura 5.1: Ilustración de un clasificador de máximo margen con dos predictores (con datos simulados; los puntos se corresponden con las observaciones y el color, negro o rojo, con la clase). La línea sólida es el hiperplano de máximo margen y los puntos sólidos son los vectores de soporte (las líneas discontinuas se corresponden con la máxima distancia del hiperplano a las observaciones).

Matemáticamente, dadas las \(n\) observaciones de entrenamiento \(\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_n\), el clasificador de máximo margen es la solución del problema de optimización \[max_{\beta_0, \beta_1,\ldots, \beta_p} M\] sujeto a \[\sum_{j=1}^p \beta_j^2 = 1\] \[ y_i(\beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + \ldots + \beta_p x_{pi}) \ge M \ \ \forall i\]

Si, como estamos suponiendo en esta sección, los datos de entrenamiento son perfectamente separables mediante un hiperplano, entonces el problema anterior va a tener solución con \(M>0\), y \(M\) va a ser el margen.

Una forma equivalente (y más conveniente) de formular el problema anterior, utilizando \(M = 1/\lVert \boldsymbol{\beta} \rVert\) con \(\boldsymbol{\beta} = (\beta_1, \beta_2, \ldots, \beta_p)\), es \[\mbox{min}_{\beta_0, \boldsymbol{\beta}} \lVert \boldsymbol{\beta} \rVert\] sujeto a \[ y_i(\beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + \ldots + \beta_p x_{pi}) \ge 1 \ \ \forall i\] El problema anterior de optimización es convexo, dado que la función objetivo es cuadrática y las restricciones son lineales.

Hay una característica de este método que es de destacar: así como en otros métodos, si se modifica cualquiera de los datos se modifica también el modelo, en este caso el modelo solo depende de los (pocos) datos que son vector soporte, y la modificación de cualquier otro dato no afecta a la construcción del modelo (siempre que, al moverse el dato, no cambie el margen).