7.4 Regresión spline adaptativa multivariante

La regresión spline adaptativa multivariante, en inglés multivariate adaptive regression splines (MARS, Friedman, 1991), es un procedimiento adaptativo para problemas de regresión que puede verse como una generalización tanto de la regresión lineal por pasos (stepwise linear regression) como de los árboles de decisión CART.

El modelo MARS es un spline multivariante lineal:
\[m(\mathbf{x}) = \beta_0 + \sum_{m=1}^M \beta_m h_m(\mathbf{x})\] (es un modelo lineal en transformaciones \(h_m(\mathbf{x})\) de los predictores originales), donde las bases \(h_m(\mathbf{x})\) se construyen de forma adaptativa empleando funciones bisagra (hinge functions) \[ h(x) = (x)_+ = \left\{ \begin{array}{ll} x & \mbox{si } x > 0 \\ 0 & \mbox{si } x \leq 0 \end{array} \right.\] y considerando como posibles nodos los valores observados de los predictores (en el caso univariante se emplean las bases de potencias truncadas con \(d=1\) descritas en la Sección 7.2.1, pero incluyendo también su versión simetrizada).

Vamos a empezar explicando el modelo MARS aditivo (sin interacciones), que funciona de forma muy parecida a los árboles de decisión CART, y después lo extenderemos al caso con interacciones. Asumimos que todas las variables predictoras son numéricas. El proceso de construcción del modelo es un proceso iterativo hacia delante (forward) que empieza con el modelo \[\hat m(\mathbf{x}) = \hat \beta_0 \] donde \(\hat \beta_0\) es la media de todas las respuestas, para a continuación considerar todos los puntos de corte (knots) posibles \(x_{ji}\) con \(i = 1, 2, \ldots, n\), \(j = 1, 2, \ldots, p\), es decir, todas las observaciones de todas las variables predictoras de la muestra de entrenamiento. Para cada punto de corte \(x_{ji}\) (combinación de variable y observación) se consideran dos bases: \[ \begin{aligned} h_1(\mathbf{x}) = h(x_j - x_{ji}) \\ h_2(\mathbf{x}) = h(x_{ji} - x_j) \end{aligned}\] y se construye el nuevo modelo \[\hat m(\mathbf{x}) = \hat \beta_0 + \hat \beta_1 h_1(\mathbf{x}) + \hat \beta_2 h_2(\mathbf{x})\] La estimación de los parámetros \(\beta_0, \beta_1, \beta_2\) se realiza de la forma estándar en regresión lineal, minimizando \(\mbox{RSS}\). De este modo se construyen muchos modelos alternativos y entre ellos se selecciona aquel que tenga un menor error de entrenamiento. En la siguiente iteración se conservan \(h_1(\mathbf{x})\) y \(h_2(\mathbf{x})\) y se añade una pareja de términos nuevos siguiendo el mismo procedimiento. Y así sucesivamente, añadiendo de cada vez dos nuevos términos. Este procedimiento va creando un modelo lineal segmentado (piecewise) donde cada nuevo término modeliza una porción aislada de los datos originales.

El tamaño de cada modelo es el número términos (funciones \(h_m\)) que este incorpora. El proceso iterativo se para cuando se alcanza un modelo de tamaño \(M\), que se consigue después de incorporar \(M/2\) cortes. Este modelo depende de \(M+1\) parámetros \(\beta_m\) con \(m=0,1,\ldots,M\). El objetivo es alcanzar un modelo lo suficientemente grande para que sobreajuste los datos, para a continuación proceder a su poda en un proceso de eliminación de variables hacia atrás (backward deletion) en el que se van eliminando las variables de una en una (no por parejas, como en la construcción). En cada paso de poda se elimina el término que produce el menor incremento en el error. Así, para cada tamaño \(\lambda = 0,1,\ldots, M\) se obtiene el mejor modelo estimado \(\hat{m}_{\lambda}\).

La selección óptima del valor del hiperparámetro \(\lambda\) puede realizarse por los procedimientos habituales tipo validación cruzada. Una alternativa mucho más rápida es utilizar validación cruzada generalizada (GCV), que es una aproximación de la validación cruzada leave-one-out, mediante la fórmula \[\mbox{GCV} (\lambda) = \frac{\mbox{RSS}}{(1-M(\lambda)/n)^2}\] donde \(M(\lambda)\) es el número de parámetros efectivos del modelo, que depende del número de términos más el número de puntos de corte utilizados penalizado por un factor (2 en el caso aditivo que estamos explicando, 3 cuando hay interacciones).

Hemos descrito un caso particular de MARS: el modelo aditivo. El modelo general solo se diferencia del caso aditivo en que se permiten interacciones, es decir, multiplicaciones entre las variables \(h_m(\mathbf{x})\). Para ello, en cada iteración durante la fase de construcción del modelo, además de considerar todos los puntos de corte, también se consideran todas las combinaciones con los términos incorporados previamente al modelo, denominados términos padre. De este modo, si resulta seleccionado un término padre \(h_l(\mathbf{x})\) (incluyendo \(h_0(\mathbf{x}) = 1\)) y un punto de corte \(x_{ji}\), después de analizar todas las posibilidades, al modelo anterior se le agrega \[\hat \beta_{m+1} h_l(\mathbf{x}) h(x_j - x_{ji}) + \hat \beta_{m+2} h_l(\mathbf{x}) h(x_{ji} - x_j)\] Es importante destacar que en cada paso se vuelven a estimar todos los parámetros \(\beta_i\).

Al igual que \(\lambda\), también el grado de interacción máxima permitida se considera un hiperparámetro del problema, aunque lo habitual es trabajar con grado 1 (modelo aditivo) o interacción de grado 2. Una restricción adicional que se impone al modelo es que en cada producto no puede aparecer más de una vez la misma variable \(X_j\).

Aunque el procedimiento de construcción del modelo realiza búsquedas exhaustivas, y en consecuencia puede parecer computacionalmente intratable, en la práctica se realiza de forma razonablemente rápida, al igual que ocurría en CART. Una de las principales ventajas de MARS es que realiza una selección automática de las variables predictoras. Aunque inicialmente pueda haber muchos predictores, y este método es adecuado para problemas de alta dimensión, en el modelo final van a aparecer muchos menos (pueden aparecer más de una vez). Además, si se utiliza un modelo aditivo su interpretación es directa, e incluso permitiendo interacciones de grado 2 el modelo puede ser interpretado. Otra ventaja es que no es necesario realizar un preprocesado de los datos, ni filtrando variables ni transformando los datos. Que haya predictores con correlaciones altas no va a afectar a la construcción del modelo (normalmente seleccionará el primero), aunque sí puede dificultar su interpretación. Aunque hemos supuesto al principio de la explicación que los predictores son numéricos, se pueden incorporar variables predictoras cualitativas siguiendo los procedimientos estándar. Por último, se puede realizar una cuantificación de la importancia de las variables de forma similar a como se hace en CART.

En conclusión, MARS utiliza splines lineales con una selección automática de los puntos de corte mediante un algoritmo avaricioso, similar al empleado en los árboles CART, tratando de añadir más puntos de corte donde aparentemente hay más variaciones en la función de regresión y menos puntos donde esta es más estable.

7.4.1 MARS con el paquete `earth`

Actualmente el paquete de referencia para MARS es earth (Enhanced Adaptive Regression Through Hinges, Milborrow, 2023)⁶⁶.

La función principal es earth() y se suelen considerar los siguientes argumentos:

earth(formula, data, glm = NULL, degree = 1, ...)

formula y data (opcional): permiten especificar la respuesta y las variables predictoras de la forma habitual (p. ej. respuesta ~ .; también admite matrices). Admite respuestas multidimensionales (ajustará un modelo para cada componente) y categóricas (las convierte en multivariantes); también predictores categóricos, aunque no permite datos faltantes.
glm: lista con los parámetros del ajuste GLM (p. ej. glm = list(family = binomial)).
degree: grado máximo de interacción; por defecto 1 (modelo aditivo).

Otros parámetros que pueden ser de interés (afectan a la complejidad del modelo en el crecimiento, a la selección del modelo final o al tiempo de computación; para más detalles ver help(earth)):

nk: número máximo de términos en el crecimiento del modelo (dimensión \(M\) de la base); por defecto min(200, max(20, 2 * ncol(x))) + 1 (puede ser demasiado pequeña si muchos de los predictores influyen en la respuesta).
thresh: umbral de parada en el crecimiento (se interpretaría como cp en los árboles CART); por defecto 0.001 (si se establece a 0 la única condición de parada será alcanzar el valor máximo de términos nk).
fast.k: número máximo de términos padre considerados en cada paso durante el crecimiento; por defecto 20, si se establece a 0 no habrá limitación.
linpreds: índice de variables que se considerarán con efecto lineal.
nprune: número máximo de términos (incluida la intersección) en el modelo final (después de la poda); por defecto no hay límite (se podrían incluir todos los creados durante el crecimiento).
pmethod: método empleado para la poda; por defecto "backward". Otras opciones son: "forward", "seqrep", "exhaustive" (emplea los métodos de selección implementados en el paquete leaps), "cv" (validación cruzada, empleando nflod) y "none" para no realizar poda.
nfold: número de grupos de validación cruzada; por defecto 0 (no se hace validación cruzada).
varmod.method: permite seleccionar un método para estimar las varianzas y, por ejemplo, poder realizar contrastes o construir intervalos de confianza (para más detalles ver ?varmod o la vignette Variance models in earth).

Utilizaremos como ejemplo inicial los datos de MASS:mcycle:

# data(mcycle, package = "MASS")
library(earth)
mars <- earth(accel ~ times, data = mcycle)
summary(mars)

## Call: earth(formula=accel~times, data=mcycle)
## 
##               coefficients
## (Intercept)       -90.9930
## h(19.4-times)       8.0726
## h(times-19.4)       9.2500
## h(times-31.2)     -10.2365
## 
## Selected 4 of 6 terms, and 1 of 1 predictors
## Termination condition: RSq changed by less than 0.001 at 6 terms
## Importance: times
## Number of terms at each degree of interaction: 1 3 (additive model)
## GCV 1119.8    RSS 133670    GRSq 0.52403    RSq 0.56632

Por defecto, el método representa un resumen de los errores de validación en la selección del modelo, la distribución empírica y el gráfico QQ de los residuos, y los residuos frente a las predicciones (ver Figura 7.13):

plot(mars)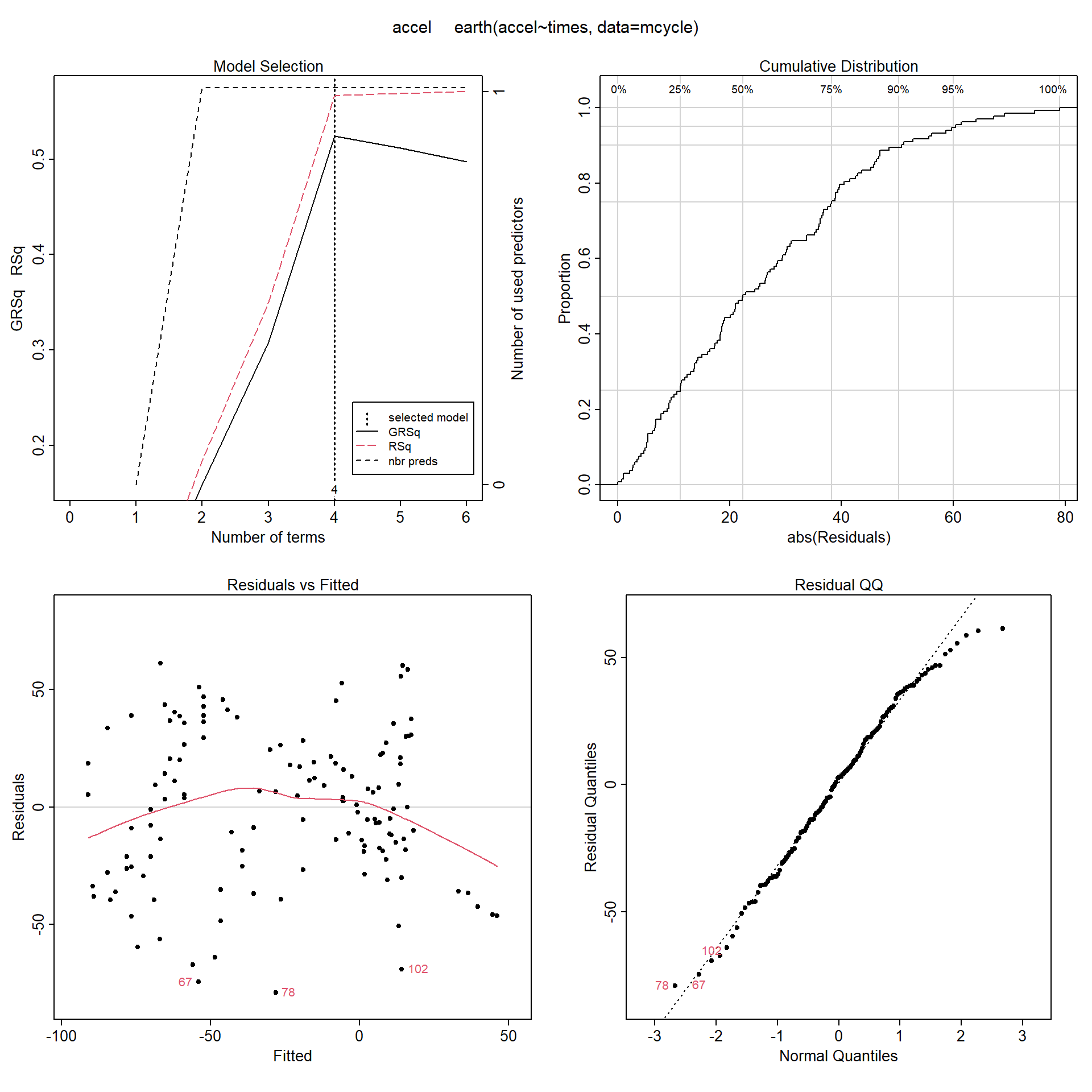

Figura 7.13: Resultados de validación del modelo MARS univariante (empleando la función earth() con parámetros por defecto y MASS:mcycle).

Si representamos el ajuste obtenido (ver Figura 7.14), vemos que con las opciones por defecto no es especialmente bueno, aunque puede ser suficiente para un análisis preliminar:

plot(accel ~ times, data = mcycle, col = 'darkgray')
lines(mcycle$times, predict(mars))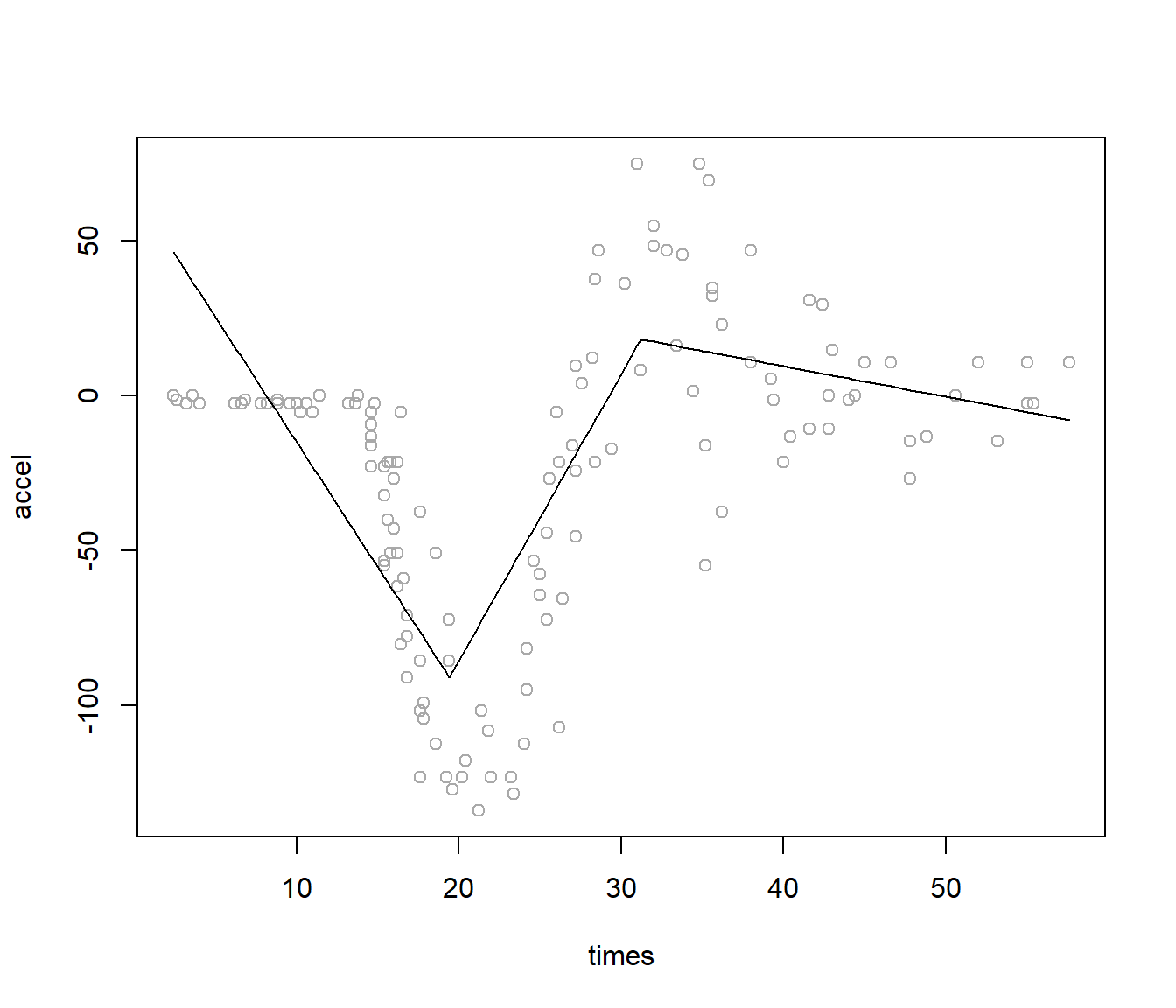

Figura 7.14: Ajuste del modelo MARS univariante (obtenido con la función earth() con parámetros por defecto) para predecir accel en función de times.

Para mejorar el ajuste, podríamos forzar la complejidad del modelo en el crecimiento (eliminando el umbral de parada y estableciendo minspan = 1 para que todas las observaciones sean potenciales nodos; ver Figura 7.15):

mars2 <- earth(accel ~ times, data = mcycle, minspan = 1, thresh = 0)
summary(mars2)

## Call: earth(formula=accel~times, data=mcycle, minspan=1, thresh=0)
## 
##               coefficients
## (Intercept)        -6.2744
## h(times-14.6)     -25.3331
## h(times-19.2)      32.9793
## h(times-25.4)     153.6992
## h(times-25.6)    -145.7474
## h(times-32)       -30.0411
## h(times-35.2)      13.7239
## 
## Selected 7 of 12 terms, and 1 of 1 predictors
## Termination condition: Reached nk 21
## Importance: times
## Number of terms at each degree of interaction: 1 6 (additive model)
## GCV 623.52    RSS 67509    GRSq 0.73498    RSq 0.78097

plot(accel ~ times, data = mcycle, col = 'darkgray')
lines(mcycle$times, predict(mars2))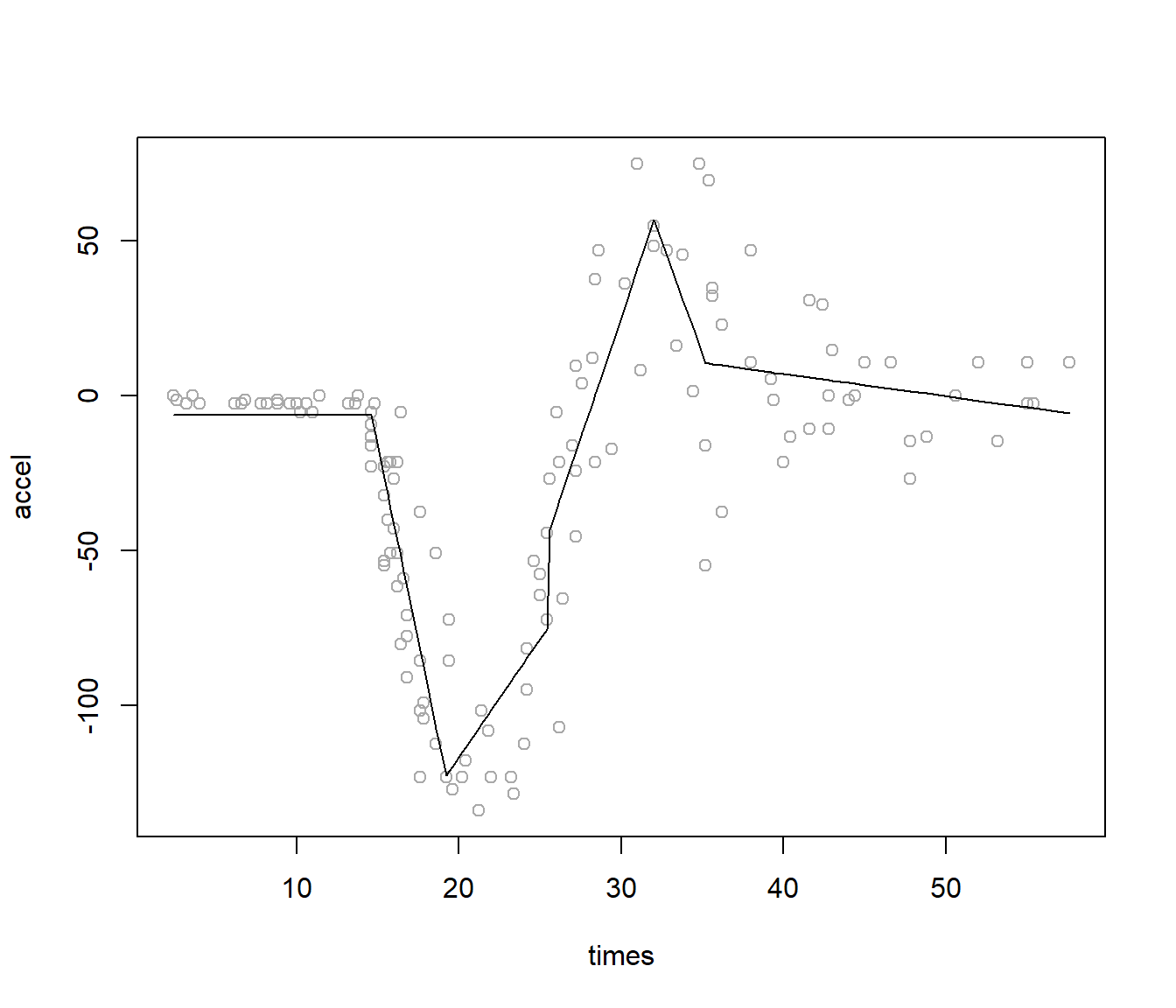

Figura 7.15: Ajuste del modelo MARS univariante (con la función earth() con parámetros minspan = 1 y thresh = 0).

Veamos a continuación un segundo ejemplo, utilizando los datos de carData::Prestige:

mars <- earth(prestige ~ education + income + women, data = Prestige,
              degree = 2, nk = 40)
summary(mars)

## Call: earth(formula=prestige~education+income+women, data=Prestige,
##             degree=2, nk=40)
## 
##                                coefficients
## (Intercept)                        19.98452
## h(education-9.93)                   5.76833
## h(income-3161)                      0.00853
## h(income-5795)                     -0.00802
## h(women-33.57)                      0.21544
## h(income-5299) * h(women-4.14)     -0.00052
## h(income-5795) * h(women-4.28)      0.00054
## 
## Selected 7 of 31 terms, and 3 of 3 predictors
## Termination condition: Reached nk 40
## Importance: education, income, women
## Number of terms at each degree of interaction: 1 4 2
## GCV 53.087    RSS 3849.4    GRSq 0.82241    RSq 0.87124

Para representar los efectos de las variables, earth utiliza las herramientas del paquete plotmo (del mismo autor; válido también para la mayoría de los modelos tratados en este libro, incluyendo mgcv::gam(); ver Figura 7.16):

plotmo(mars)

##  plotmo grid:    education income women
##                      10.54   5930  13.6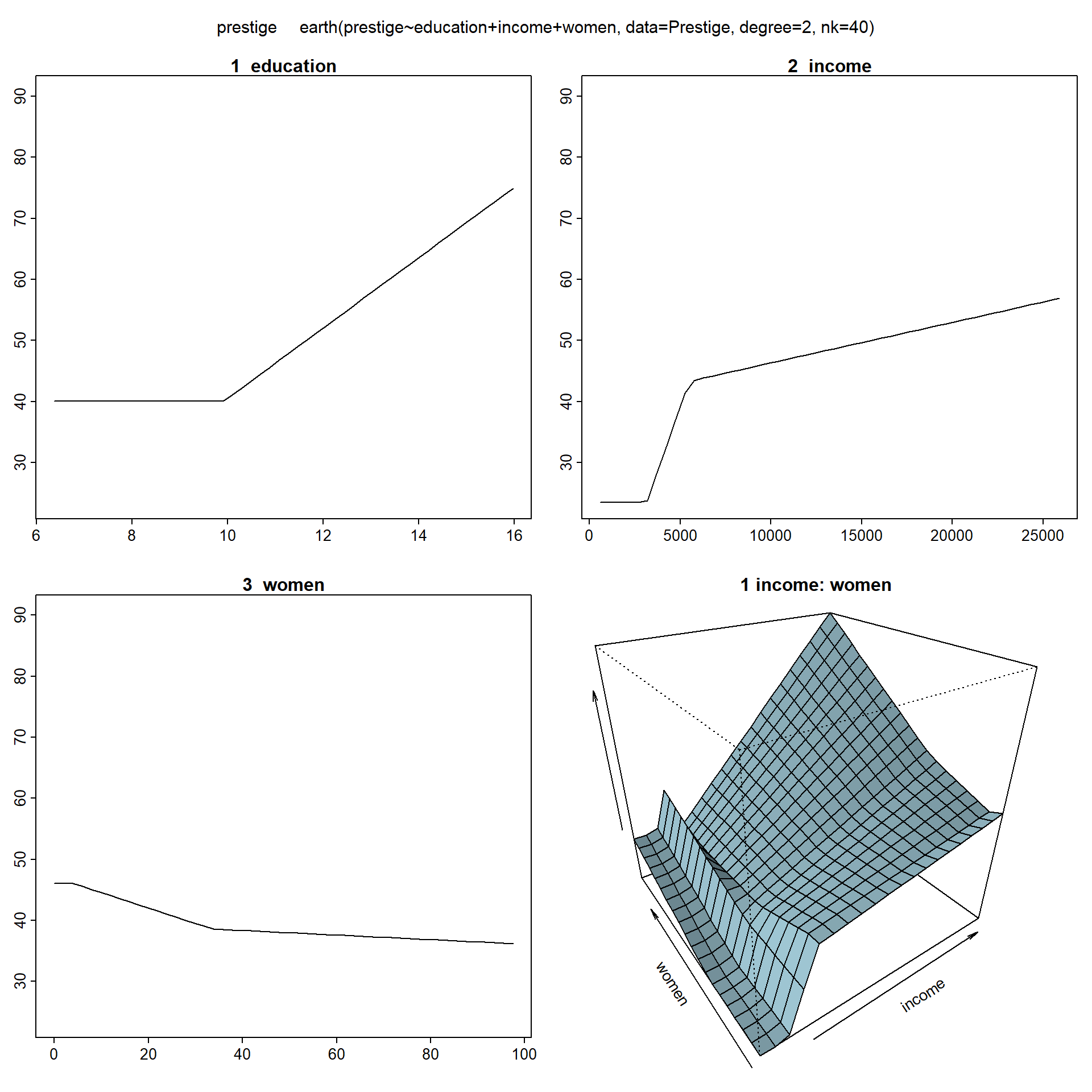

Figura 7.16: Efectos parciales de las componentes del modelo MARS ajustado.

También podemos obtener la importancia de las variables mediante la función evimp() y representarla gráficamente utilizando el método plot.evimp(); ver Figura 7.17:

varimp <- evimp(mars)
varimp

##           nsubsets   gcv    rss
## education        6 100.0  100.0
## income           5  36.0   40.3
## women            3  16.3   22.0

plot(varimp)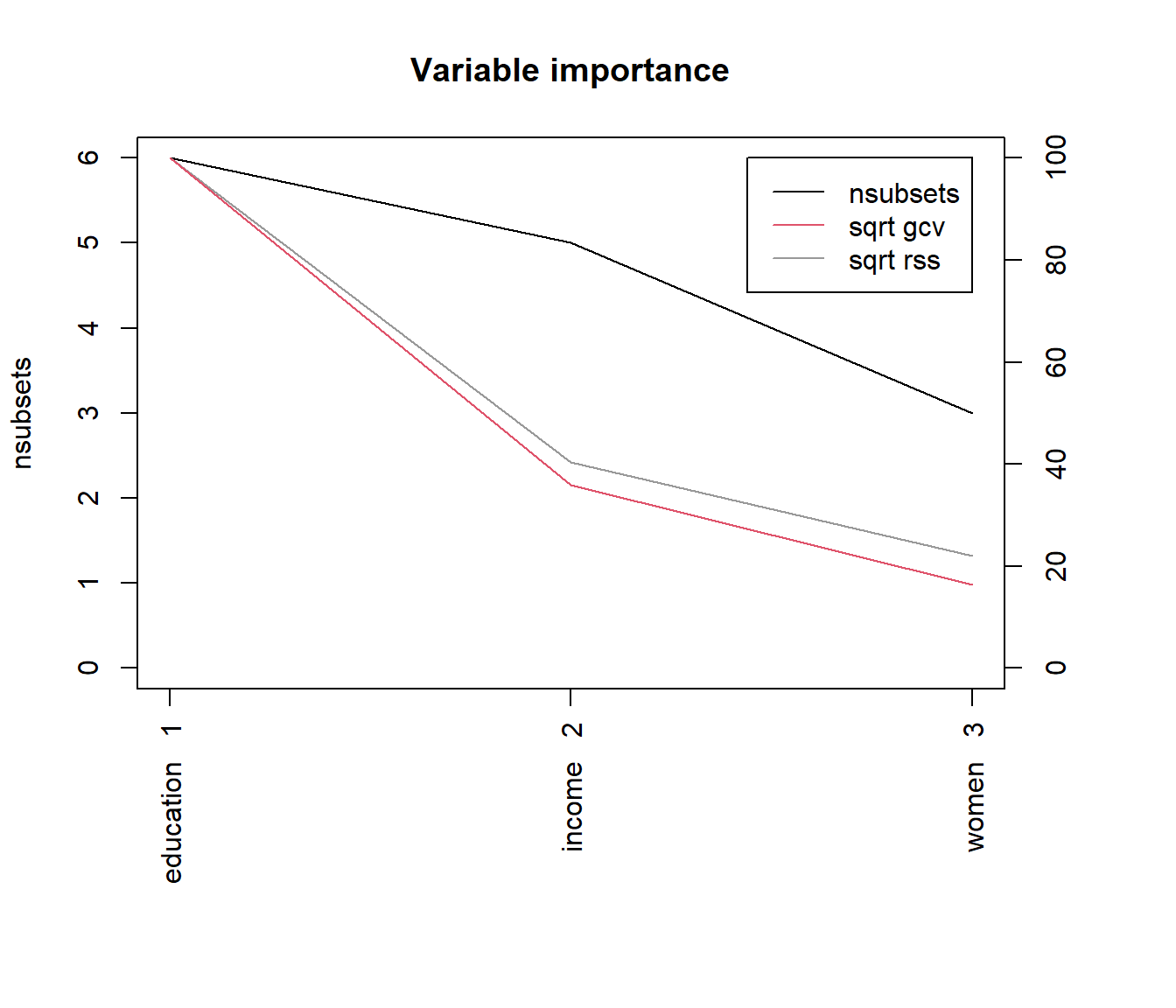

Figura 7.17: Importancia de los predictores incluidos en el modelo MARS.

Para finalizar, queremos destacar que se puede tener en cuenta este modelo como punto de partida para ajustar un modelo GAM más flexible (como se mostró en la Sección 7.3). En este caso, el ajuste GAM equivalente al modelo MARS anterior sería el siguiente:

fit.gam <- gam(prestige ~ s(education) + s(income, women), data = Prestige)
summary(fit.gam)

## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## prestige ~ s(education) + s(income, women)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   46.833      0.679      69   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##                  edf Ref.df    F p-value    
## s(education)    2.80   3.49 25.1  <2e-16 ***
## s(income,women) 4.89   6.29 10.0  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.841   Deviance explained = 85.3%
## GCV = 51.416  Scale est. = 47.032    n = 102

Las estimaciones de los efectos pueden variar considerablemente entre ambos modelos, ya que el modelo GAM es mucho más flexible, como se muestra en la Figura 7.18. En esta gráfica se representan los efectos principales de los predictores y el efecto de la interacción entre income y women, que difieren considerablemente de los correspondiente al modelo MARS mostrados en la Figura 7.16.

plotmo(fit.gam)

##  plotmo grid:    education income women
##                      10.54   5930  13.6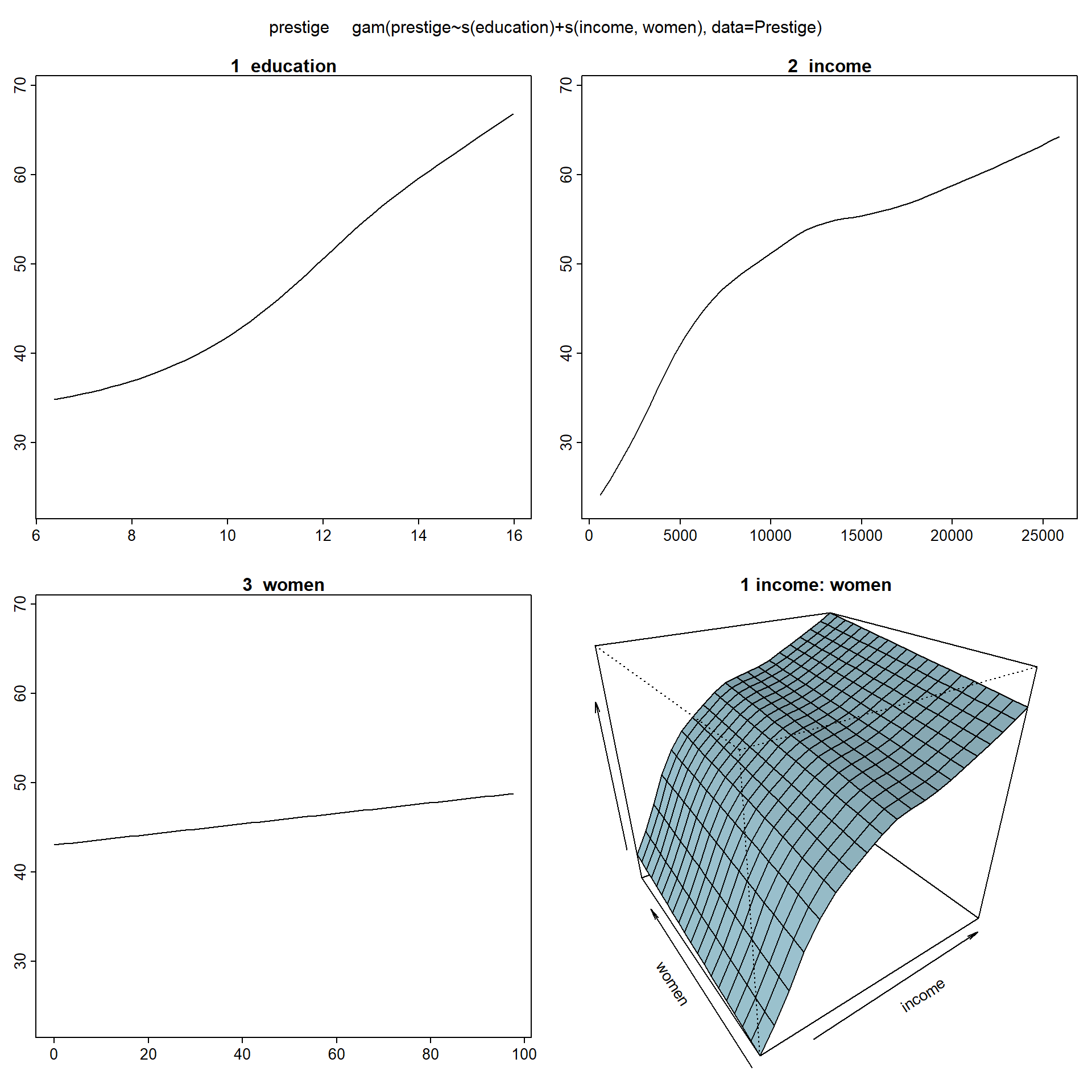

Figura 7.18: Efectos parciales de las componentes del modelo GAM con interacción.

En este caso concreto, la representación del efecto de la interacción puede dar lugar a confusión. Realmente, no hay observaciones con ingresos altos y un porcentaje elevado de mujeres, y se está realizando una extrapolación en esta zona. Esto se puede ver claramente en la Figura 7.19, donde se representa el efecto parcial de la interacción empleando las herramientas del paquete mgcv:

plot(fit.gam, scheme = 2, select = 2)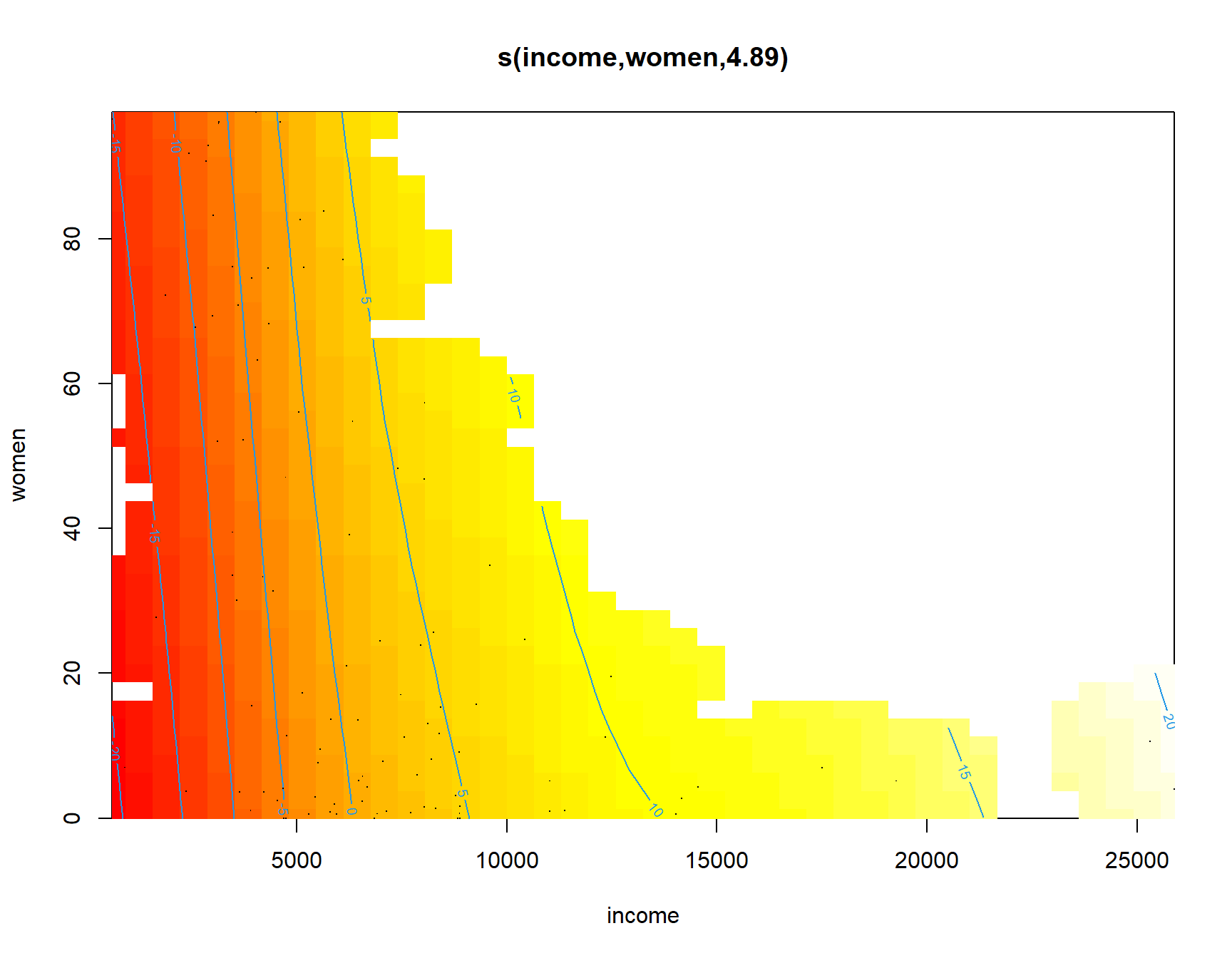

Figura 7.19: Efecto parcial de la interacción income:women.

Lo anterior nos podría hacer sospechar que el efecto de la interacción no es significativo. Además, si ajustamos el modelo sin interacción obtenemos un coeficiente de determinación ajustado mejor:

fit.gam2 <- gam(prestige ~ s(education) + s(income) + s(women), 
                data = Prestige)
summary(fit.gam2)

## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## prestige ~ s(education) + s(income) + s(women)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   46.833      0.656    71.3   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##               edf Ref.df     F p-value    
## s(education) 2.81   3.50 26.39  <2e-16 ***
## s(income)    3.53   4.40 11.72  <2e-16 ***
## s(women)     2.21   2.74  3.71   0.022 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.852   Deviance explained = 86.4%
## GCV = 48.484  Scale est. = 43.941    n = 102

El procedimiento clásico sería realizar un contraste de hipótesis, como se mostró en la Sección 7.3.2:

anova(fit.gam2, fit.gam, test = "F")

## Analysis of Deviance Table
## 
## Model 1: prestige ~ s(education) + s(income) + s(women)
## Model 2: prestige ~ s(education) + s(income, women)
##   Resid. Df Resid. Dev     Df Deviance    F Pr(>F)   
## 1      90.4       4062                               
## 2      91.2       4388 -0.865     -326 8.59 0.0061 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Este resultado nos haría pensar que el efecto de la interacción es significativo. Sin embargo, si nos fijamos en los resultados intermedios de la tabla, la diferencia entre los grados de libertad residuales de ambos modelo es negativa. Algo que en principio no debería ocurrir, ya que el modelo completo (con interacción) debería tener menos grados de libertad residuales que el modelo reducido (sin interacción). Esto es debido a que en el ajuste de un modelo GAM, por defecto, los grados de libertad de las componentes se seleccionan automáticamente y, en este caso concreto, la complejidad del modelo ajustado sin interacción resultó ser mayor (como se puede observar al comparar la columna edf del sumario de ambos modelos). Resumiendo, el modelo sin interacción no sería una versión reducida del modelo con interacción y no deberíamos emplear el contraste anterior. En cualquier caso, la recomendación en aprendizaje estadístico es emplear métodos de remuestreo, en lugar de contrastes de hipótesis, para seleccionar el modelo.

Ejercicio 7.5 Siguiendo con el ejemplo anterior de los datos Prestige, compara los errores de validación cruzada dejando uno fuera (LOOCV) de ambos modelos, con y sin interacción entre income y women, para decidir cuál sería preferible.

7.4.2 MARS con el paquete `caret`

En esta sección, emplearemos como ejemplo el conjunto de datos earth::Ozone1 y seguiremos el procedimiento habitual en aprendizaje estadístico:

# data(ozone1, package = "earth")
df <- ozone1  
set.seed(1)
nobs <- nrow(df)
itrain <- sample(nobs, 0.8 * nobs)
train <- df[itrain, ]
test <- df[-itrain, ]

De los varios métodos basados en earth que implementa caret, emplearemos el algoritmo original:

library(caret)
# names(getModelInfo("[Ee]arth")) # 4 métodos
modelLookup("earth")

##   model parameter          label forReg forClass probModel
## 1 earth    nprune         #Terms   TRUE     TRUE      TRUE
## 2 earth    degree Product Degree   TRUE     TRUE      TRUE

Para la selección de los hiperparámetros óptimos, consideramos una rejilla de búsqueda personalizada (ver Figura 7.20):

tuneGrid <- expand.grid(degree = 1:2, nprune = floor(seq(2, 20, len = 10)))
set.seed(1)
caret.mars <- train(O3 ~ ., data = train, method = "earth",
    trControl = trainControl(method = "cv", number = 10), tuneGrid = tuneGrid)
caret.mars

## Multivariate Adaptive Regression Spline 
## 
## 264 samples
##   9 predictor
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 238, 238, 238, 236, 237, 239, ... 
## Resampling results across tuning parameters:
## 
##   degree  nprune  RMSE    Rsquared  MAE   
##   1        2      4.8429  0.63667   3.8039
##   1        4      4.5590  0.68345   3.4880
##   1        6      4.3458  0.71420   3.4132
##   1        8      4.2566  0.72951   3.2203
##   1       10      4.1586  0.74368   3.1819
##   1       12      4.1284  0.75096   3.1422
##   1       14      4.0697  0.76006   3.0615
##   1       16      4.0588  0.76092   3.0588
##   1       18      4.0588  0.76092   3.0588
##   1       20      4.0588  0.76092   3.0588
##   2        2      4.8429  0.63667   3.8039
##   2        4      4.6528  0.67260   3.5400
##  [ reached getOption("max.print") -- omitted 8 rows ]
## 
## RMSE was used to select the optimal model using the smallest value.
## The final values used for the model were nprune = 10 and degree = 2.

ggplot(caret.mars, highlight = TRUE)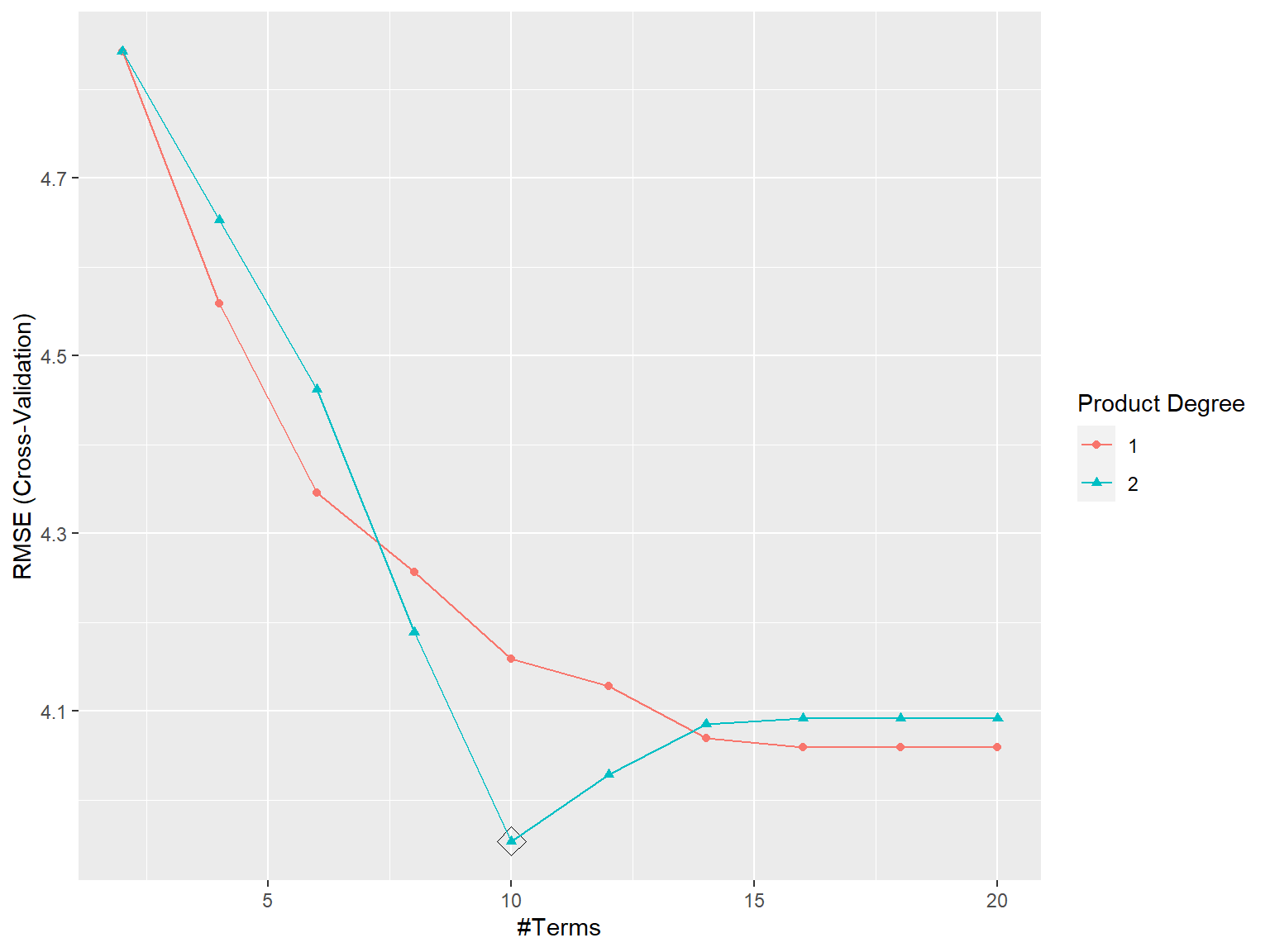

Errores RMSE de validación cruzada de los modelos MARS en función del numero de términos nprune y del orden máximo de interacción degree, resaltando la combinación óptima.

Figura 7.20: Errores RMSE de validación cruzada de los modelos MARS en función del numero de términos nprune y del orden máximo de interacción degree, resaltando la combinación óptima.

El modelo final contiene 10 términos con interacciones. Podemos analizarlo con las herramientas de earth:

summary(caret.mars$finalModel)

## Call: earth(x=matrix[264,9], y=c(4,13,16,3,6,2...), keepxy=TRUE, degree=2,
##             nprune=10)
## 
##                             coefficients
## (Intercept)                     11.64820
## h(dpg-15)                       -0.07439
## h(ibt-110)                       0.12248
## h(17-vis)                       -0.33633
## h(vis-17)                       -0.01104
## h(101-doy)                      -0.10416
## h(doy-101)                      -0.02368
## h(wind-3) * h(1046-ibh)         -0.00234
## h(humidity-52) * h(15-dpg)      -0.00479
## h(60-humidity) * h(ibt-110)     -0.00276
## 
## Selected 10 of 21 terms, and 7 of 9 predictors (nprune=10)
## Termination condition: Reached nk 21
## Importance: humidity, ibt, dpg, doy, wind, ibh, vis, temp-unused, ...
## Number of terms at each degree of interaction: 1 6 3
## GCV 13.842    RSS 3032.6    GRSq 0.78463    RSq 0.8199

Representamos los efectos parciales de las componentes, separando los efectos principales (Figura 7.21) de las interacciones (Figura 7.22):

# plotmo(caret.mars$finalModel)
plotmo(caret.mars$finalModel, degree2 = 0, caption = "")

##  plotmo grid:    vh wind humidity temp    ibh dpg   ibt vis   doy
##                5770    5     64.5   62 2046.5  24 169.5 100 213.5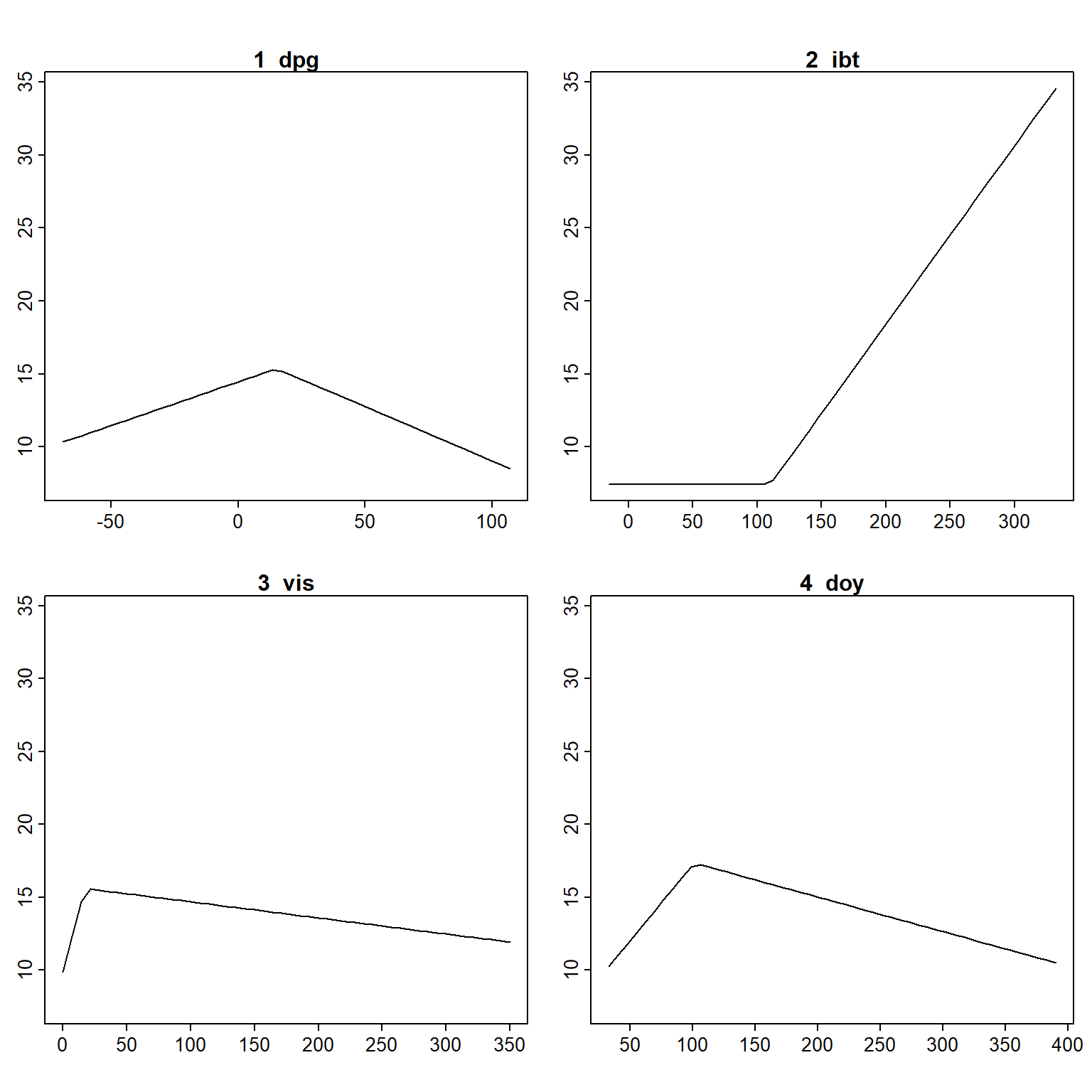

Figura 7.21: Efectos parciales principales del modelo MARS ajustado con caret.

plotmo(caret.mars$finalModel, degree1 = 0, caption = "")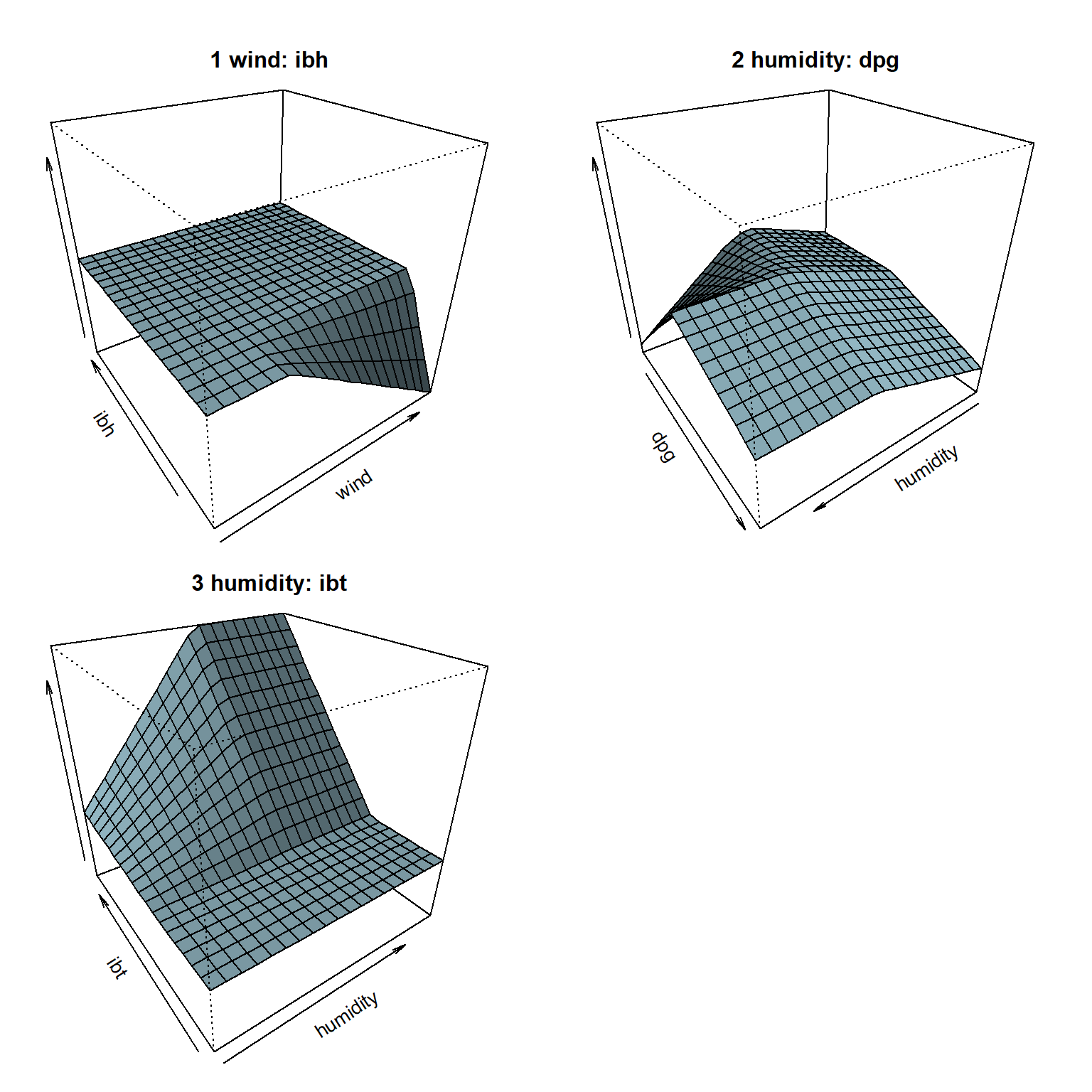

Figura 7.22: Efectos parciales principales de las interacciones del modelo MARS ajustado con caret.

Finalmente, evaluamos la precisión de las predicciones en la muestra de test con el procedimiento habitual:

pred <- predict(caret.mars, newdata = test)
accuracy(pred, test$O3)

##        me      rmse       mae       mpe      mape r.squared 
##   0.48179   4.09524   3.07644 -14.12889  41.26020   0.74081

Ejercicio 7.6 Continuando con el conjunto de datos mpae::bodyfat empleado en capítulos anteriores, particiona los datos y ajusta un modelo para predecir el porcentaje de grasa corporal (bodyfat), mediante regresión spline adaptativa multivariante (MARS) con el método "earth" del paquete caret:

Utiliza validación cruzada con 10 grupos para seleccionar los valores “óptimos” de los hiperparámetros considerando degree = 1:2 y nprune = 1:6, y fija nk = 60.
Estudia el efecto de los predictores incluidos en el modelo final y obtén medidas de su importancia.
Evalúa las predicciones en la muestra de test (genera el correspondiente gráfico y obtén medidas de error).

Ejercicio 7.7 Vuelve a ajustar el modelo aditivo no paramétrico del ejercicio anterior, con la misma partición, pero empleando la función gam() del paquete mcgv:

Incluye los efectos no lineales de los predictores seleccionados por el método MARS obtenido en el ejercicio anterior.
Representa los efectos de los predictores (incluyendo los residuos añadiendo los argumentos residuals = TRUE y pch = 1) y estudia si sería razonable asumir que el de alguno de ellos es lineal o simplificar el modelo de alguna forma.
Ajusta también el modelo bodyfat ~ s(abdomen) + s(weight).
Evalúa las predicciones en la muestra de test y compara los resultados con los obtenidos en el ejercicio anterior.

Ejercicio 7.8 Repite los ejercicios 7.6 y 7.7 anteriores, pero ahora utilizando el conjunto de datos mpae::bfan y considerando como respuesta el nivel de grasa corporal (bfan). Recuerda que en el ajuste aditivo logístico mgcv::gam() habrá que incluir family = binomial, y type = "response" en el correspondiente método predict() para obtener estimaciones de las probabilidades.

Bibliografía

Friedman, J. (1991). Multivariate Adaptive Regression Splines. The Annals of Statistics, 19(1), 1-67. https://doi.org/10.1214/aos/1176347963

Milborrow, S. (2023). earth: Multivariate Adaptive Regression Splines. https://cran.r-project.org/package=earth

Desarrollado a partir de la función mda::mars() de T. Hastie y R. Tibshirani. Utiliza este nombre porque MARS está registrado para un uso comercial por Salford Systems.↩︎