6.2 Métodos de reducción de la dimensión
Otra alternativa, para tratar de reducir la varianza de los modelos lineales, es transformar los predictores considerando \(k < p\) combinaciones lineales: \[Z_j = a_{1j}X_{1} + a_{2j}X_{2} + \ldots + a_{pj}X_{p}\] con \(j = 1, \ldots, k\), denominadas componentes (o variables latentes), y posteriormente ajustar un modelo de regresión lineal empleándolas como nuevos predictores: \[Y = \alpha_0 + \alpha_1 Z_1 + \ldots + \alpha_k Z_k + \varepsilon\]
Adicionalmente, si se seleccionan los coeficientes \(a_{ij}\) (denominados cargas o pesos) de forma que \[\sum_{i=1}^p a_{ij}a_{il} = 0, \text{ si } j \neq l,\] las componentes serán ortogonales y se evitarán posibles problemas de colinealidad. De esta forma se reduce la dimensión del problema, pasando de \(p + 1\) a \(k + 1\) coeficientes a estimar, lo cual en principio disminuirá la varianza, especialmente si \(p\) es grande en comparación con \(n\). Por otra parte, también podríamos expresar el modelo final en función de los predictores originales, con coeficientes: \[\beta_i = \sum_{j=1}^k \alpha_j a_{ij}\] Es decir, se ajusta un modelo lineal con restricciones, lo que en principio incrementará el sesgo (si \(k = p\) sería equivalente a ajustar un modelo lineal sin restricciones). Además, podríamos interpretar los coeficientes \(\alpha_j\) como los efectos de las componentes del modo tradicional, pero resultaría más complicado interpretar los efectos de los predictores originales.
También hay que tener en cuenta que al considerar combinaciones lineales, si las hipótesis estructurales de linealidad, homocedasticidad, normalidad o independencia no son asumibles en el modelo original, es de esperar que tampoco lo sean en el modelo transformado (se podrían emplear las herramientas descritas en la Sección 2.1.3 para su análisis).
Hay una gran variedad de algoritmos para obtener estas componentes. En esta sección consideraremos las dos aproximaciones más utilizadas: componentes principales y mínimos cuadrados parciales.
También hay numerosos paquetes de R que implementan métodos de este tipo (pls, plsRglm…), incluyendo caret.
6.2.1 Regresión por componentes principales (PCR)
Una de las aproximaciones tradicionales, cuando se detecta la presencia de colinealidad, consiste en aplicar el método de componentes principales a los predictores. El análisis de componentes principales (principal component analysis, PCA) es un método muy utilizado de aprendizaje no supervisado, que permite reducir el número de dimensiones tratando de recoger la mayor parte de la variabilidad de los datos originales, en este caso de los predictores (para más detalles sobre PCA ver, por ejemplo, el Capítulo 10 de James et al., 2021).
Al aplicar PCA a los predictores \(X_1, \ldots, X_p\) se obtienen componentes ordenadas según la variabilidad explicada de forma descendente. La primera componente es la que recoge el mayor porcentaje de la variabilidad total (se corresponde con la dirección de mayor variación de las observaciones). Las siguientes componentes se seleccionan entre las direcciones ortogonales a las anteriores y de forma que recojan la mayor parte de la variabilidad restante. Además, estas componentes son normalizadas, de forma que: \[\sum_{i=1}^p a_{ij}^2 = 1\] (se busca una transformación lineal ortonormal). En la práctica, esto puede llevarse a cabo de manera sencilla a partir de la descomposición espectral de la matriz de covarianzas muestrales, aunque normalmente se estandarizan previamente los datos (i. e. se emplea la matriz de correlaciones). Por tanto, si se pretende emplear estas componentes para ajustar un modelo de regresión, habrá que conservar los parámetros de estas transformaciones para poder aplicarlas a nuevas observaciones.
Normalmente, se seleccionan las primeras \(k\) componentes de forma que expliquen la mayor parte de la variabilidad de los datos (los predictores en este caso). En PCR (principal component regression, Massy, 1965) se confía en que estas componentes recojan también la mayor parte de la información sobre la respuesta, pero podría no ser el caso.
Aunque se pueden utilizar las funciones printcomp() y lm() del paquete base, emplearemos por comodidad la función pcr() del paquete pls (Mevik y Wehrens, 2007), ya que incorpora validación cruzada para seleccionar el número de componentes y facilita el cálculo de nuevas predicciones.
Los argumentos principales de esta función son:
pcr(formula, ncomp, data, scale = FALSE, center = TRUE,
validation = c("none", "CV", "LOO"), segments = 10,
segment.type = c("random", "consecutive", "interleaved"), ...)ncomp: número máximo de componentes (ajustará modelos desde 1 hastancompcomponentes).scale,center: normalmente valores lógicos indicando si los predictores serán reescalados (divididos por su desviación estándar y centrados, restando su media).validation: determina el tipo de validación, puede ser"none"(ninguna, se empleará el modelo ajustado con toda la muestra de entrenamiento),"LOO"(VC dejando uno fuera) y"CV"(VC por grupos). En este último caso, los grupos de validación se especifican mediantesegments(número de grupos) ysegment.type(por defecto aleatorios; para más detalles consultar la ayuda demvrCv()).
Como ejemplo continuaremos con los datos de grasa corporal. Reescalaremos los predictores y emplearemos validación cruzada por grupos para seleccionar el número de componentes:
library(pls)
set.seed(1)
pcreg <- pcr(bodyfat ~ ., data = train, scale = TRUE, validation = "CV")Podemos obtener un resumen de los resultados de validación (evolución de los errores de validación cruzada) y del ajuste en la muestra de entrenamiento (evolución de la proporción de variabilidad explicada de los predictores y de la respuesta) con el método summary():
summary(pcreg)## Data: X dimension: 196 13
## Y dimension: 196 1
## Fit method: svdpc
## Number of components considered: 13
##
## VALIDATION: RMSEP
## Cross-validated using 10 random segments.
## (Intercept) 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps
## CV 8.253 6.719 5.778 5.327 5.023 5.050 5.082
## adjCV 8.253 6.713 5.763 5.310 5.014 5.041 5.077
## 7 comps 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps
## CV 4.935 4.887 4.899 4.881 4.929 4.449 4.457
## adjCV 4.907 4.873 4.887 4.870 4.925 4.436 4.444
##
## TRAINING: % variance explained
## 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps 8 comps
## X 61.55 72.80 79.90 85.42 89.33 91.98 94.17 96.06
## bodyfat 35.51 53.27 59.62 64.52 64.53 64.58 67.25 67.33
## 9 comps 10 comps 11 comps 12 comps 13 comps
## X 97.63 98.76 99.37 99.85 100.00
## bodyfat 67.33 67.62 67.64 73.65 73.67Aunque suele resultar más cómodo representar gráficamente estos valores (ver Figura 6.6).
Por ejemplo empleando RMSEP() para acceder a los errores de validación57:
# validationplot(pcreg, legend = "topright")
rmsep.cv <- RMSEP(pcreg)
plot(rmsep.cv, legend = "topright")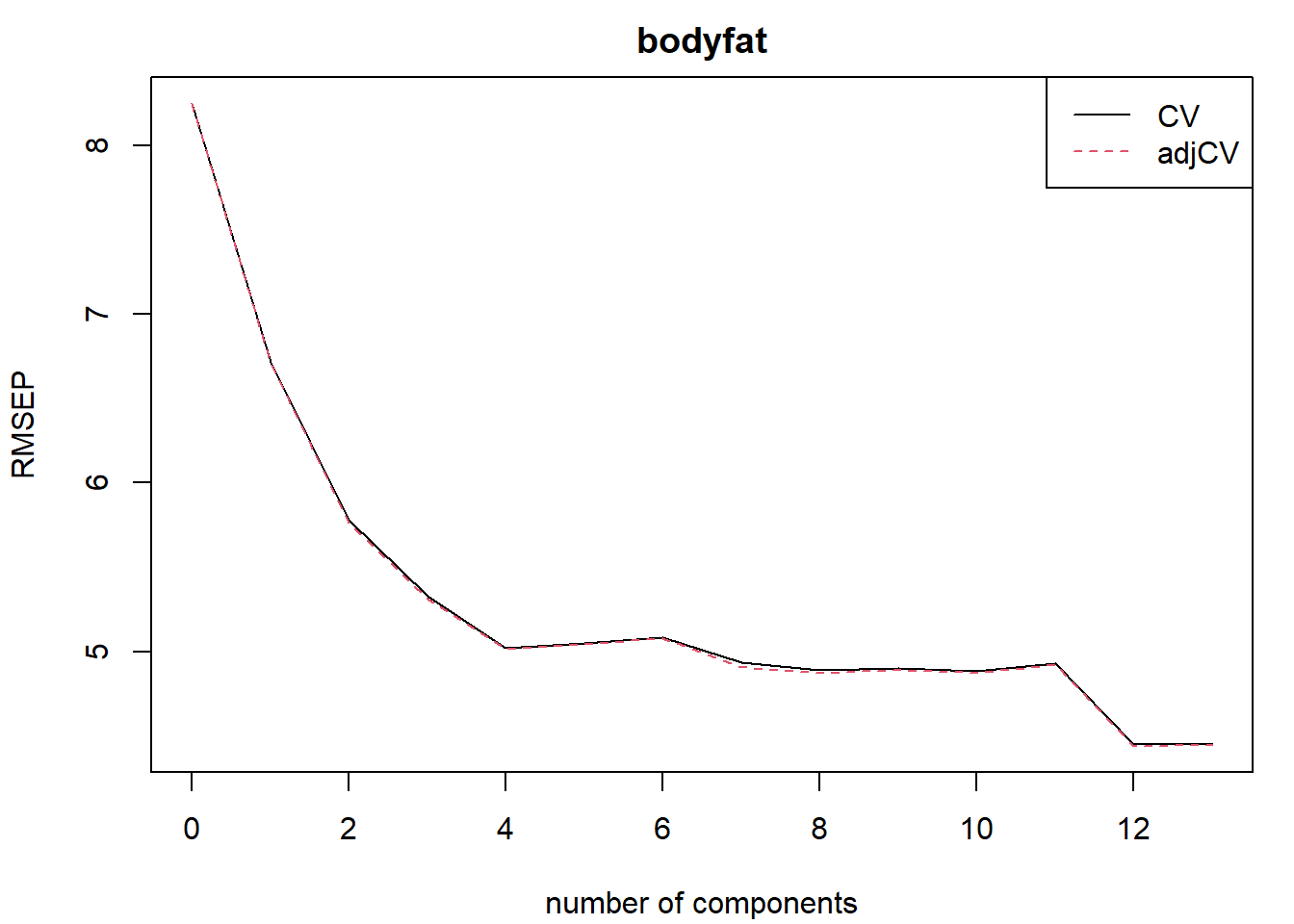
Figura 6.6: Errores de validación cruzada en función del número de componentes en el ajuste mediante PCR.
ncomp.op <- with(rmsep.cv, comps[which.min(val[2, 1, ])]) # mínimo adjCV RMSEPEn este caso, empleando el criterio de menor error de validación cruzada se seleccionaría un número elevado de componentes, el mínimo se alcanzaría con 12 componentes (casi como ajustar un modelo lineal con todos los predictores).
Los coeficientes de los predictores originales con el modelo seleccionado serían58:
coef(pcreg, ncomp = 12, intercept = TRUE)## , , 12 comps
##
## bodyfat
## (Intercept) 21.141410
## age 0.523514
## weight 0.730388
## height -0.915070
## neck -0.625323
## chest -1.361064
## abdomen 9.175811
## hip -1.587609
## thigh 0.576468
## knee 0.050425
## ankle -0.025927
## biceps 0.422922
## forearm 0.595122
## wrist -1.781728Finalmente evaluamos su precisión:
pred <- predict (pcreg , test, ncomp = 12)
accuracy(pred, obs)## me rmse mae mpe mape r.squared
## 1.46888 3.96040 3.24888 1.40161 18.71800 0.75754Alternativamente, podríamos emplear el método "pcr" de caret.
Por ejemplo, seleccionando el número de componentes mediante la regla de un error estándar (ver Figura 6.7):
library(caret)
modelLookup("pcr")## model parameter label forReg forClass probModel
## 1 pcr ncomp #Components TRUE FALSE FALSEset.seed(1)
trControl <- trainControl(method = "cv", number = 10,
selectionFunction = "oneSE")
caret.pcr <- train(bodyfat ~ ., data = train, method = "pcr",
preProcess = c("zv", "center", "scale"),
trControl = trControl, tuneGrid = data.frame(ncomp = 1:10))
caret.pcr## Principal Component Analysis
##
## 196 samples
## 13 predictor
##
## Pre-processing: centered (13), scaled (13)
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 177, 176, 176, 177, 177, 177, ...
## Resampling results across tuning parameters:
##
## ncomp RMSE Rsquared MAE
## 1 6.5808 0.36560 5.3235
## 2 5.6758 0.53027 4.7039
## 3 5.2136 0.59429 4.3556
## 4 4.9757 0.62975 4.0940
## 5 5.0257 0.62283 4.1352
## 6 5.1269 0.60878 4.2177
## 7 4.9522 0.62418 4.0541
## 8 4.9588 0.62119 4.0375
## 9 4.9612 0.61994 4.0361
## 10 4.9603 0.61727 4.0152
##
## RMSE was used to select the optimal model using the one SE rule.
## The final value used for the model was ncomp = 3.ggplot(caret.pcr, highlight = TRUE)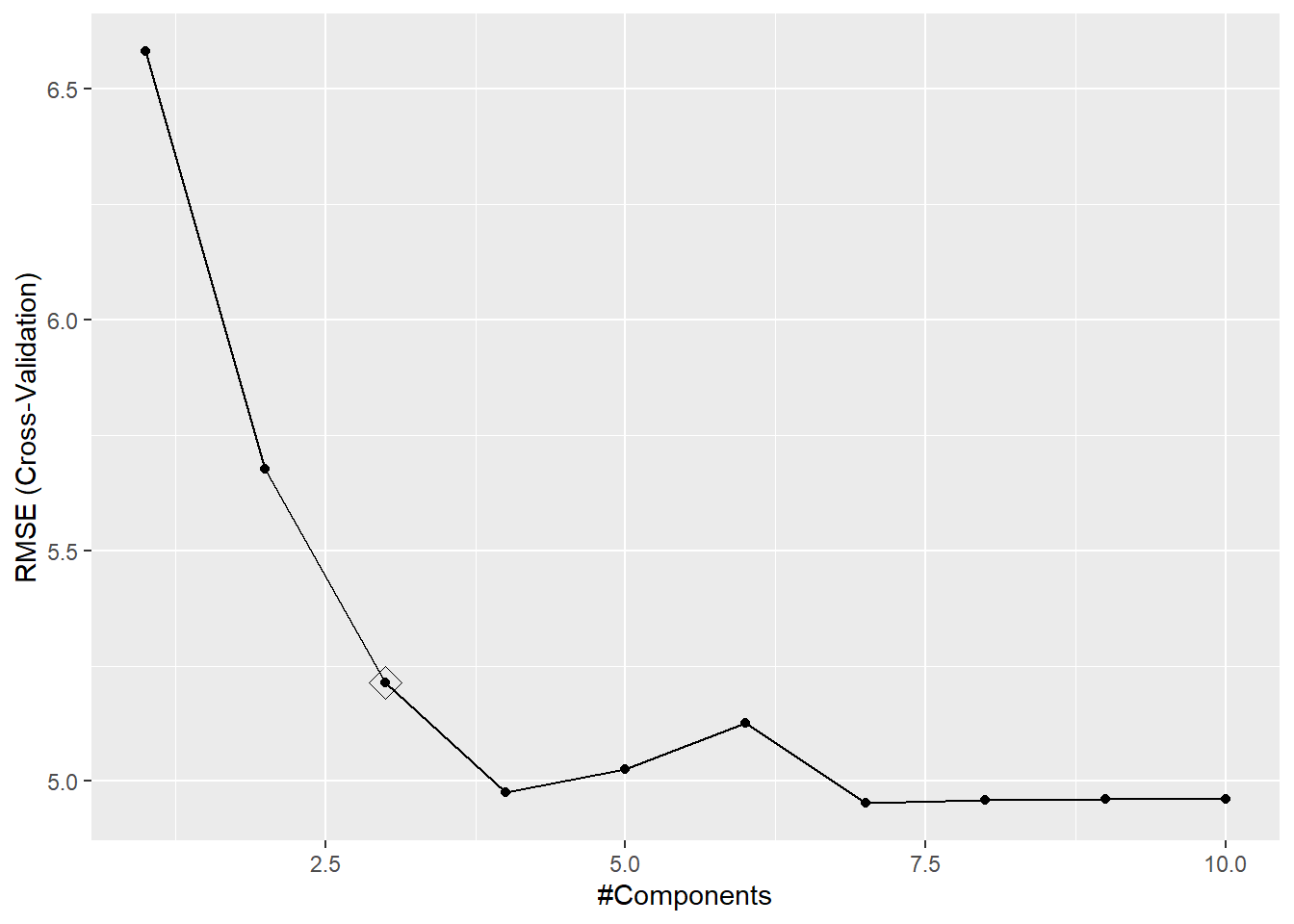
Figura 6.7: Errores de validación cruzada en función del número de componentes en el ajuste mediante PCR y valor óptimo según la regla de un error estándar.
pred <- predict(caret.pcr, newdata = test)
accuracy(pred, obs)## me rmse mae mpe mape r.squared
## 1.21285 5.20850 4.33211 -5.71168 28.14310 0.58064Al incluir más componentes se aumenta la proporción de variabilidad explicada de los predictores,
pero esto no está relacionado con su utilidad para explicar la respuesta.
No va a haber problemas de colinealidad aunque incluyamos muchas componentes, pero se tendrán que estimar más coeficientes y va a disminuir su precisión.
Sería más razonable obtener las componentes principales y después aplicar un método de selección.
Por ejemplo, podemos combinar el método de preprocesado "pca" de caret con un método de selección de variables59 (ver Figura 6.8):
set.seed(1)
caret.pcrsel <- train(bodyfat ~ ., data = train, method = "leapSeq",
preProcess = c("zv", "center", "scale", "pca"),
trControl = trControl, tuneGrid = data.frame(nvmax = 1:6))
caret.pcrsel## Linear Regression with Stepwise Selection
##
## 196 samples
## 13 predictor
##
## Pre-processing: centered (13), scaled (13), principal component
## signal extraction (13)
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 177, 176, 176, 177, 177, 177, ...
## Resampling results across tuning parameters:
##
## nvmax RMSE Rsquared MAE
## 1 6.5808 0.36560 5.3235
## 2 5.6758 0.53027 4.7039
## 3 5.4083 0.57633 4.4092
## 4 5.0320 0.62265 4.1378
## 5 4.8434 0.64078 3.9361
## 6 4.9449 0.62511 4.0321
##
## RMSE was used to select the optimal model using the one SE rule.
## The final value used for the model was nvmax = 4.ggplot(caret.pcrsel, highlight = TRUE)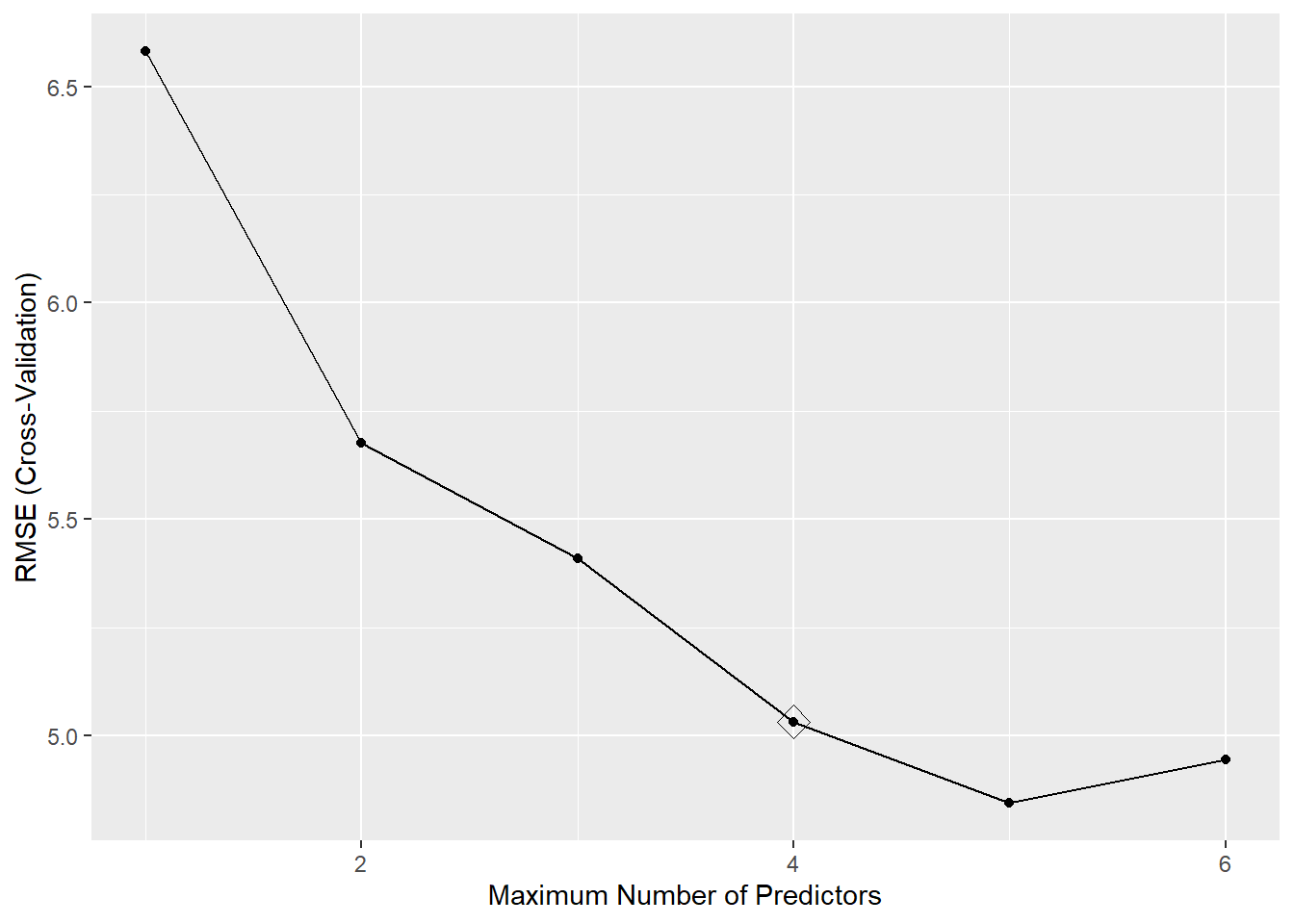
Figura 6.8: Errores de validación cruzada en función del número de componentes en el ajuste mediante PCR con selección por pasos y valor óptimo según la regla de un error estándar.
No obstante, en este caso las primeras componentes también resultan ser aparentemente las de mayor utilidad para explicar la respuesta, ya que se seleccionaron las cuatro primeras:
with(caret.pcrsel, coef(finalModel, bestTune$nvmax))## (Intercept) PC1 PC2 PC3 PC4
## 18.8036 1.7341 -2.8685 2.1570 -2.1531Para finalizar evaluamos también la precisión del modelo obtenido:
pred <- predict(caret.pcrsel, newdata = test)
accuracy(pred, obs)## me rmse mae mpe mape r.squared
## 0.83749 4.76899 3.89344 -6.10279 25.16598 0.648436.2.2 Regresión por mínimos cuadrados parciales (PLSR)
Como ya se comentó, en PCR las componentes se determinan con el objetivo de explicar la variabilidad de los predictores, ignorando por completo la respuesta. Por el contrario, en PLSR (partial least squares regression, Wold et al., 1983) se construyen las componentes \(Z_1, \ldots, Z_k\) teniendo en cuenta desde un principio el objetivo final de predecir linealmente la respuesta.
Hay varios procedimientos para seleccionar los pesos \(a_{ij}\), pero la idea es asignar mayor peso a los predictores que están más correlacionados con la respuesta (o con los correspondientes residuos al ir obteniendo nuevas componentes), considerando siempre direcciones ortogonales (ver, por ejemplo, la Sección 6.3.2 de James et al., 2021).
Continuando con el ejemplo anterior, emplearemos en primer lugar la función plsr() del paquete pls, que tiene los mismos argumentos que la función pcr() descrita en la sección anterior60:
set.seed(1)
plsreg <- plsr(bodyfat ~ ., data = train, scale = TRUE, validation = "CV")
summary(plsreg)## Data: X dimension: 196 13
## Y dimension: 196 1
## Fit method: kernelpls
## Number of components considered: 13
##
## VALIDATION: RMSEP
## Cross-validated using 10 random segments.
## (Intercept) 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps
## CV 8.253 6.279 4.969 4.809 4.652 4.550 4.474
## adjCV 8.253 6.273 4.965 4.798 4.637 4.541 4.458
## 7 comps 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps
## CV 4.466 4.451 4.454 4.455 4.455 4.456 4.457
## adjCV 4.452 4.438 4.442 4.442 4.442 4.443 4.444
##
## TRAINING: % variance explained
## 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps 8 comps
## X 60.53 71.8 78.48 81.90 86.35 88.12 90.16 92.96
## bodyfat 44.34 65.1 68.47 71.07 72.35 73.62 73.66 73.67
## 9 comps 10 comps 11 comps 12 comps 13 comps
## X 95.50 96.51 97.82 98.44 100.00
## bodyfat 73.67 73.67 73.67 73.67 73.67# validationplot(plsreg, legend = "topright")
rmsep.cv <- RMSEP(plsreg)
plot(rmsep.cv, legend = "topright")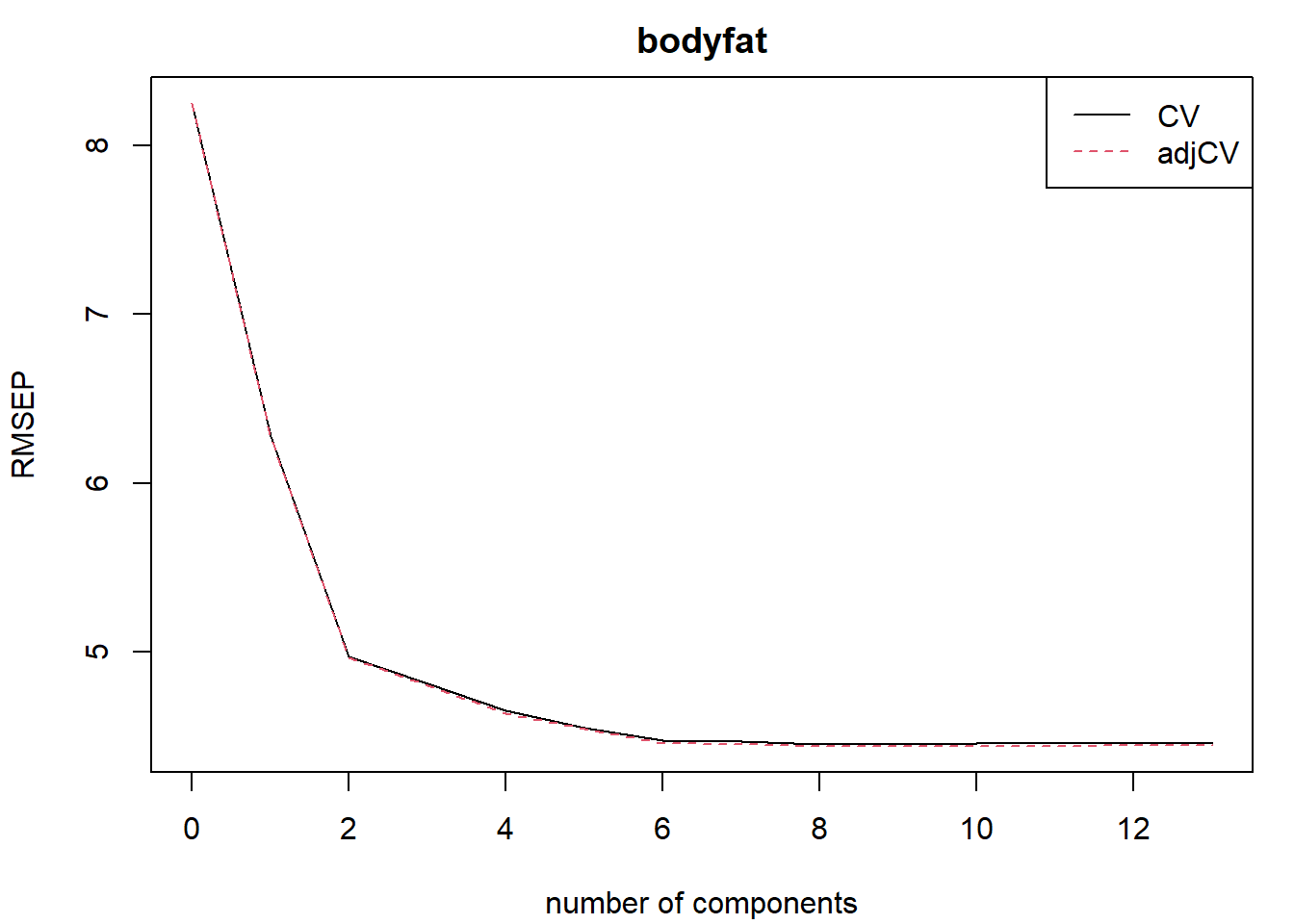
Figura 6.9: Error cuadrático medio de validación cruzada en función del número de componentes en el ajuste mediante PLS.
ncomp.op <- with(rmsep.cv, comps[which.min(val[2, 1, ])]) # mínimo adjCV RMSEPEn este caso el mínimo se alcanza con 8 componentes, pero, a la vista de la Figura 6.9, parece que 6 (o incluso 2) sería un valor más razonable. Podemos obtener los coeficientes de los predictores del modelo seleccionado:
coef(plsreg, ncomp = 6, intercept = TRUE)## , , 6 comps
##
## bodyfat
## (Intercept) 16.54393
## age 0.63007
## weight 0.42119
## height -0.82098
## neck -0.55223
## chest -1.37545
## abdomen 9.14806
## hip -1.27990
## thigh 0.76228
## knee -0.23770
## ankle 0.08447
## biceps 0.40080
## forearm 0.60030
## wrist -1.80885y evaluar su precisión:
pred.pls <- predict(plsreg , test, ncomp = 6)
accuracy(pred.pls, obs)## me rmse mae mpe mape r.squared
## 1.4373 3.9255 3.2329 1.2006 18.7601 0.7618Empleamos también el método "pls" de caret seleccionando el número de componentes mediante la regla de un error estándar (ver Figura 6.10):
modelLookup("pls")## model parameter label forReg forClass probModel
## 1 pls ncomp #Components TRUE TRUE TRUEset.seed(1)
caret.pls <- train(bodyfat ~ ., data = train, method = "pls",
preProcess = c("zv", "center", "scale"),
trControl = trControl, tuneGrid = data.frame(ncomp = 1:10))
caret.pls## Partial Least Squares
##
## 196 samples
## 13 predictor
##
## Pre-processing: centered (13), scaled (13)
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 177, 176, 176, 177, 177, 177, ...
## Resampling results across tuning parameters:
##
## ncomp RMSE Rsquared MAE
## 1 6.1572 0.44386 4.9987
## 2 4.9669 0.63414 4.1385
## 3 4.8262 0.64034 3.9733
## 4 4.7833 0.64563 3.9540
## 5 4.6810 0.66197 3.8776
## 6 4.5704 0.68981 3.7961
## 7 4.5855 0.68780 3.8110
## 8 4.5613 0.69161 3.7855
## 9 4.5566 0.69237 3.7800
## 10 4.5671 0.69087 3.7897
##
## RMSE was used to select the optimal model using the one SE rule.
## The final value used for the model was ncomp = 5.ggplot(caret.pls, highlight = TRUE)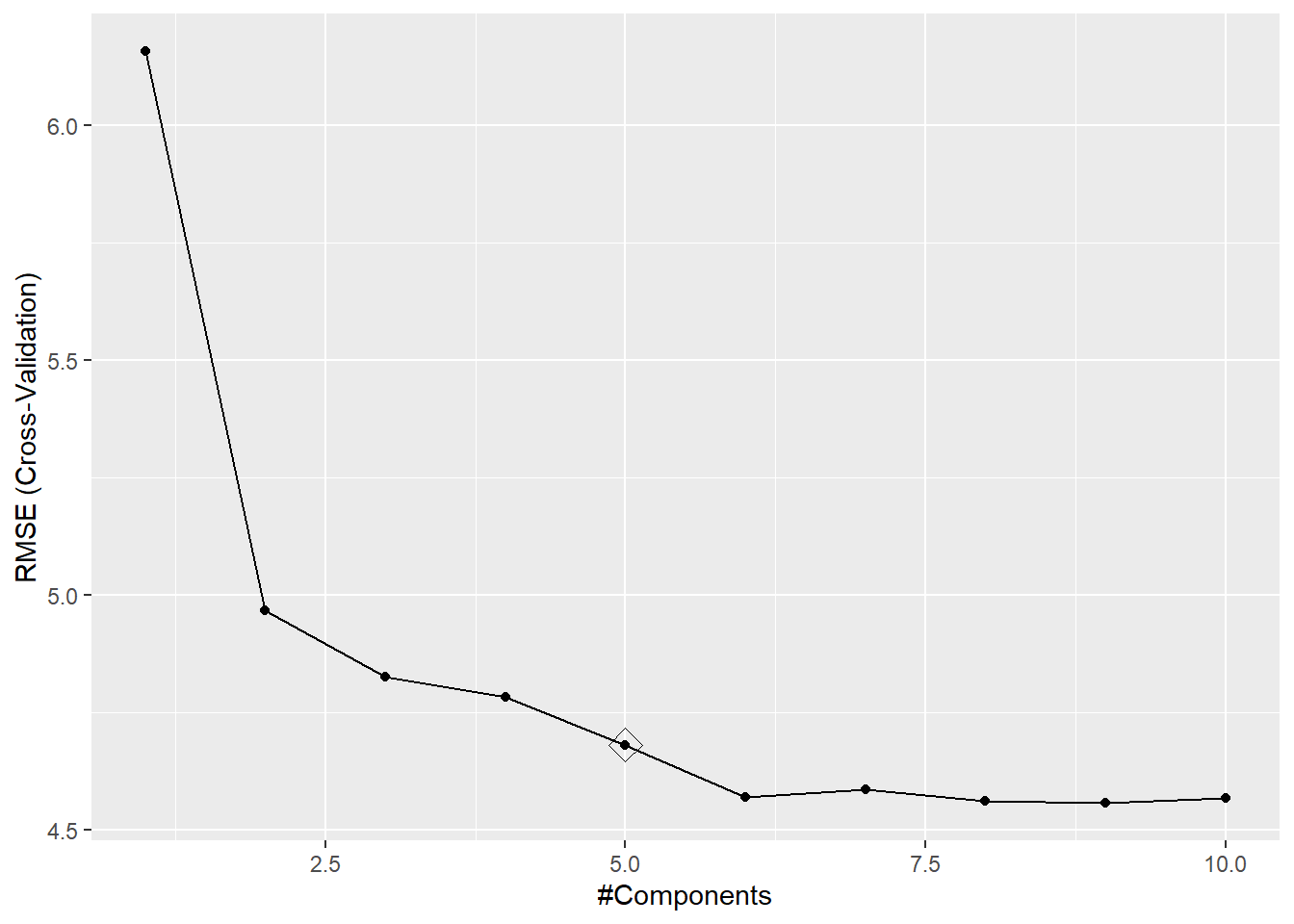
Figura 6.10: Errores de validación cruzada en función del número de componentes en el ajuste mediante PLS.
pred <- predict(caret.pls, newdata = test)
accuracy(pred, obs)## me rmse mae mpe mape r.squared
## 1.58389 4.14455 3.50307 0.82895 20.26616 0.73447En la práctica se suelen obtener resultados muy similares empleando PCR, PLSR o ridge regression.
Todos ellos son modelos lineales, por lo que el principal problema es que no sean suficientemente flexibles para explicar adecuadamente lo que ocurre con los datos (puede que no sea adecuado asumir que el efecto de algún predictor es lineal).
En este problema concreto, el mejor resultado se obtuvo con el ajuste con plsr(), aunque si representamos las observaciones frente a las predicciones (ver Figura 6.11):
pred.plot(pred.pls, obs, xlab = "Predicción", ylab = "Observado")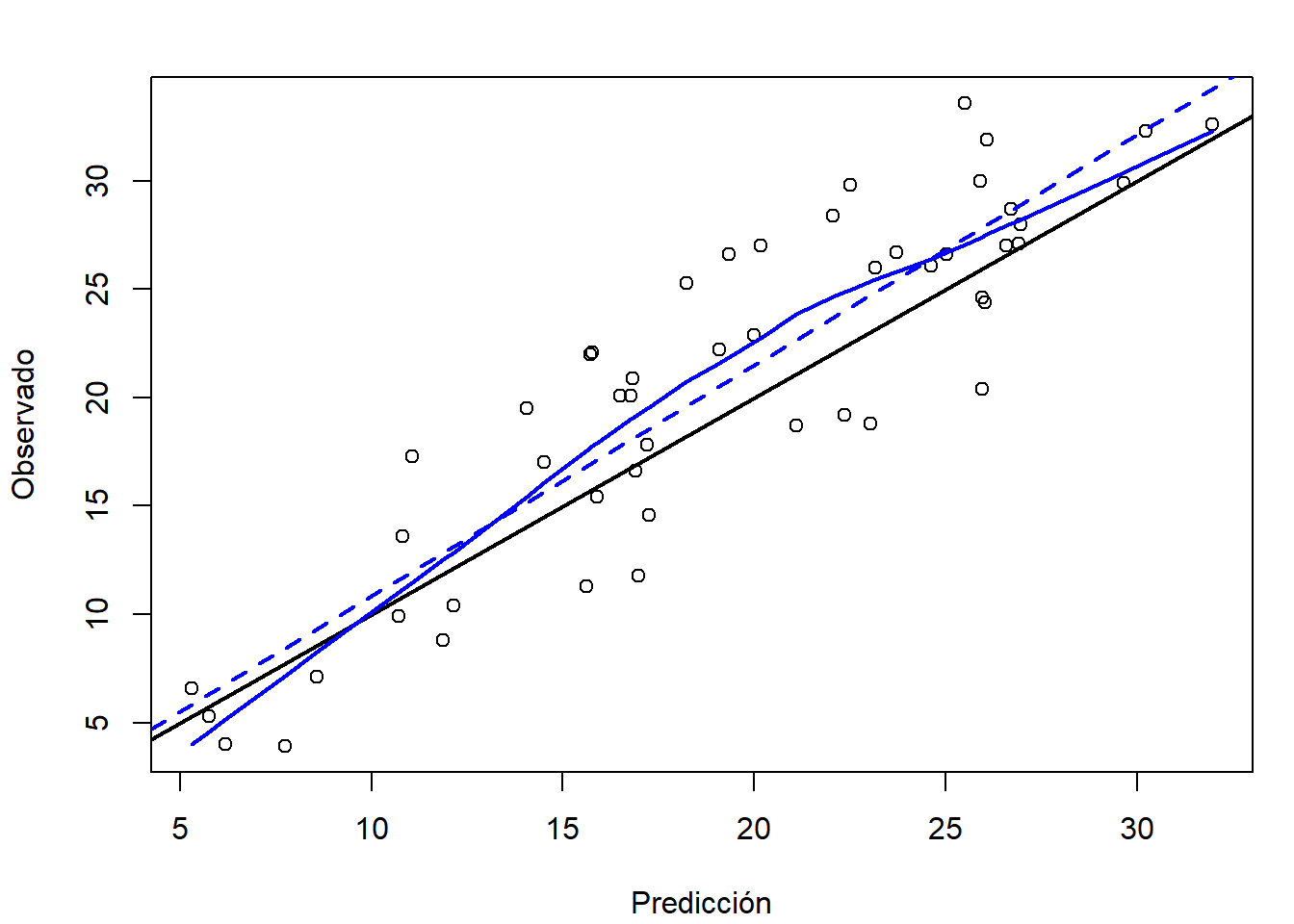
Figura 6.11: Gráfico de dispersión de observaciones frente a predicciones, del ajuste lineal con plsr(), en la muestra de test.
parece que se debería haber incluido un término cuadrático (coincidiendo con lo observado en las secciones 2.1.3 y 2.1.4).
Como comentarios finales, el método PCR (Sección 6.2) se extiende de forma inmediata al caso de modelos generalizados, simplemente cambiando el tipo de modelo ajustado.
También están disponibles métodos PLSR para modelos generalizados (p. ej. paquete plsRglm, Bertrand y Maumy, 2023).
En cualquier caso, caret ajustará un modelo generalizado si la respuesta es un factor.
Ejercicio 6.2 Continuando con el Ejercicio 6.1 y utilizando la misma partición, vuelve a clasificar los individuos según su nivel de grasa corporal (bfan), pero ahora:
Ajusta un modelo de regresión logística por componentes principales, con el método
"glmStepAIC"decarety preprocesado"pca".Ajusta un modelo de regresión logística por mínimos cuadrados parciales con el método
"pls"decaret.Interpreta los modelos obtenidos, evalúa la capacidad predictiva en la muestra
testy compara los resultados (también con los del Ejercicio 6.1).
Bibliografía
"adjCV"es una estimación de validación cruzada con corrección de sesgo.↩︎También se pueden analizar distintos aspectos del ajuste (predicciones, coeficientes, puntuaciones, cargas, biplots, cargas de correlación o gráficos de validación) con el método
plot.mvr().↩︎Esta forma de proceder se podría emplear con otros modelos que puedan tener problemas de colinealidad, como los lineales generalizados.↩︎
Realmente, ambas funciones llaman internamente a
mvr(), donde están implementadas distintas proyecciones (verhelp(pls.options), o Mevik y Wehrens, 2007).↩︎