6.1 Métodos de regularización
Como ya se comentó en el Capítulo 2, el procedimiento habitual para ajustar un modelo de regresión lineal es emplear mínimos cuadrados, es decir, utilizar como criterio de error la suma de cuadrados residual \[\mbox{RSS} = \sum\limits_{i=1}^{n}\left( y_{i} - \beta_0 - \boldsymbol{\beta}^t \mathbf{x}_{i} \right)^{2}\]
Si el modelo lineal es razonablemente adecuado, utilizar \(\mbox{RSS}\) va a dar lugar a estimaciones con poco sesgo, y si además \(n\gg p\), entonces el modelo también va a tener poca varianza (bajo las hipótesis estructurales, la estimación es insesgada y además de varianza mínima entre todas las técnicas insesgadas). Las dificultades surgen cuando \(p\) es grande o cuando hay correlaciones altas entre las variables predictoras: tener muchas variables dificulta la interpretación del modelo, y si además hay problemas de colinealidad o se incumple \(n\gg p\), entonces la estimación del modelo va a tener mucha varianza y el modelo estará sobreajustado. La solución pasa por forzar a que el modelo tenga menos complejidad para así reducir su varianza. Una forma de conseguirlo es mediante la regularización (regularization o shrinkage) de la estimación de los parámetros \(\beta_1, \beta_2,\ldots, \beta_p\), que consiste en considerar todas las variables predictoras, pero forzando a que algunos de los parámetros se estimen mediante valores muy próximos a cero, o directamente con ceros. Esta técnica va a provocar un pequeño aumento en el sesgo, pero a cambio una notable reducción en la varianza y una interpretación más sencilla del modelo resultante.
Hay dos formas básicas de lograr esta simplificación de los parámetros (con la consiguiente simplificación del modelo), utilizando una penalización cuadrática (norma \(L_2\)) o en valor absoluto (norma \(L_1\)):
Ridge regression (Hoerl y Kennard, 1970) \[\mbox{min}_{\beta_0, \boldsymbol{\beta}} \mbox{RSS} + \lambda\sum_{j=1}^{p}\beta_{j}^{2}\]
Equivalentemente, \[\mbox{min}_{\beta_0, \boldsymbol{\beta}} \mbox{RSS}\] sujeto a \[\sum_{j=1}^{p}\beta_{j}^{2} \le s\]
LASSO (least absolute shrinkage and selection operator, Tibshirani, 1996) \[\mbox{min}_{\beta_0, \boldsymbol{\beta}} RSS + \lambda\sum_{j=1}^{p}|\beta_{j}|\]
Equivalentemente, \[\mbox{min}_{\beta_0, \boldsymbol{\beta}} \mbox{RSS}\] sujeto a \[\sum_{j=1}^{p}|\beta_{j}| \le s\]
Una formulación unificada consiste en considerar el problema \[\mbox{min}_{\beta_0, \boldsymbol{\beta}} RSS + \lambda\sum_{j=1}^{p}|\beta_{j}|^d\]
Si \(d=0\), la penalización consiste en el número de variables utilizadas, por tanto se corresponde con el problema de selección de variables; \(d=1\) se corresponde con LASSO y \(d=2\) con ridge.
La ventaja de utilizar LASSO es que tiende a forzar a que algunos parámetros sean cero, con lo cual también se realiza una selección de las variables más influyentes. Por el contrario, ridge regression tiende a incluir todas las variables predictoras en el modelo final, si bien es cierto que algunas con parámetros muy próximos a cero: de este modo va a reducir el riesgo del sobreajuste, pero no resuelve el problema de la interpretabilidad. Otra posible ventaja de utilizar LASSO es que cuando hay variables predictoras correlacionadas tiene tendencia a seleccionar una y anular las demás (esto también se puede ver como un inconveniente, ya que pequeños cambios en los datos pueden dar lugar a modelos distintos), mientras que ridge tiende a darles igual peso.
Dos generalizaciones de LASSO son least angle regression (LARS, Efron et al., 2004) y elastic net (Zou y Hastie, 2005). Elastic net combina las ventajas de ridge y LASSO, minimizando \[\mbox{min}_{\beta_0, \boldsymbol{\beta}} \ \mbox{RSS} + \lambda \left( \frac{1 - \alpha}{2}\sum_{j=1}^{p}\beta_{j}^{2} + \alpha \sum_{j=1}^{p}|\beta_{j}| \right)\] siendo \(\alpha\), \(0 \leq \alpha \leq 1\), un hiperparámetro adicional que determina la combinación lineal de ambas penalizaciones.
Es muy importante estandarizar (centrar y reescalar) las variables predictoras antes de realizar estas técnicas. Fijémonos en que, así como \(\mbox{RSS}\) es insensible a los cambios de escala, la penalización es muy sensible. Previa estandarización, el término independiente \(\beta_0\) (que no interviene en la penalización) tiene una interpretación muy directa, ya que \[\widehat \beta_0 = \bar y =\sum_{i=1}^n \frac{y_i}{n}\]
Los dos métodos de regularización comentados dependen del hiperparámetro \(\lambda\) (equivalentemente, \(s\)). Es importante seleccionar adecuadamente el valor del hiperparámetro, por ejemplo utilizando validación cruzada. Hay algoritmos muy eficientes que permiten el ajuste, tanto de ridge regression como de LASSO, de forma conjunta (simultánea) para todos los valores de \(\lambda\).
6.1.1 Implementación en R
Hay varios paquetes que implementan estos métodos: h2o, elasticnet, penalized, lasso2, biglasso, etc., pero el paquete glmnet (Friedman et al., 2023) utiliza una de las más eficientes.
Sin embargo, este paquete no emplea formulación de modelos, hay que establecer la respuesta y y la matriz numérica x correspondiente a las variables explicativas.
Por tanto, no se pueden incluir directamente predictores categóricos, hay que codificarlos empleando variables auxiliares numéricas.
Se puede emplear la función model.matrix() (o Matrix::sparse.model.matrix() si el conjunto de datos es muy grande) para construir la matriz de diseño x a partir de una fórmula (alternativamente, se pueden emplear las herramientas implementadas en el paquete caret).
Además, tampoco admite datos faltantes.
La función principal es glmnet():
glmnet(x, y, family, alpha = 1, lambda = NULL, ...)family: familia del modelo lineal generalizado (ver Sección 2.2); por defecto"gaussian"(modelo lineal con ajuste cuadrático), también admite"binomial","poisson","multinomial","cox"o"mgaussian"(modelo lineal con respuesta multivariante).alpha: parámetro \(\alpha\) de elasticnet \(0 \leq \alpha \leq 1\). Por defectoalpha = 1penalización LASSO (alpha = 0para ridge regression).lambda: secuencia (opcional) de valores de \(\lambda\); si no se especifica se establece una secuencia por defecto (en base a los argumentos adicionalesnlambdaylambda.min.ratio). Se devolverán los ajustes para todos los valores de esta secuencia (también se podrán obtener posteriormente para otros valores).
Entre los métodos disponibles para el objeto resultante, coef() y predict() permiten obtener los coeficientes y las predicciones para un valor concreto de \(\lambda\), que se debe especificar mediante el argumento55 s = valor.
Para seleccionar el valor “óptimo” del hiperparámetro \(\lambda\) (mediante validación cruzada) se puede emplear cv.glmnet():
cv.glmnet(x, y, family, alpha, lambda, type.measure = "default",
nfolds = 10, ...)Esta función también devuelve los ajustes con toda la muestra de entrenamiento (en la componente $glmnet.fit) y se puede emplear el resultado directamente para predecir o obtener los coeficientes del modelo.
Por defecto, selecciona \(\lambda\) mediante la regla de “un error estándar” de Breiman et al. (1984) (componente $lambda.1se), aunque también calcula el valor óptimo (componente $lambda.min; que se puede seleccionar estableciendo s = "lambda.min").
Para más detalles, consultar la vignette del paquete An Introduction to glmnet.
Continuaremos con el ejemplo de los datos de grasa corporal empleado en la Sección 2.1 (con predictores numéricos y sin datos faltantes):
library(glmnet)
library(mpae)
data(bodyfat)
df <- bodyfat
set.seed(1)
nobs <- nrow(df)
itrain <- sample(nobs, 0.8 * nobs)
train <- df[itrain, ]
test <- df[-itrain, ]
x <- as.matrix(train[-1])
y <- train$bodyfat6.1.2 Ejemplo: ridge regression
Podemos ajustar modelos de regresión ridge (con la secuencia de valores de \(\lambda\) por defecto) con la función glmnet() con alpha=0 (ridge penalty).
Con el método plot(), podemos representar la evolución de los coeficientes en función de la penalización (etiquetando las curvas con el índice de la variable si label = TRUE; ver Figura 6.1).
fit.ridge <- glmnet(x, y, alpha = 0)
plot(fit.ridge, xvar = "lambda", label = TRUE)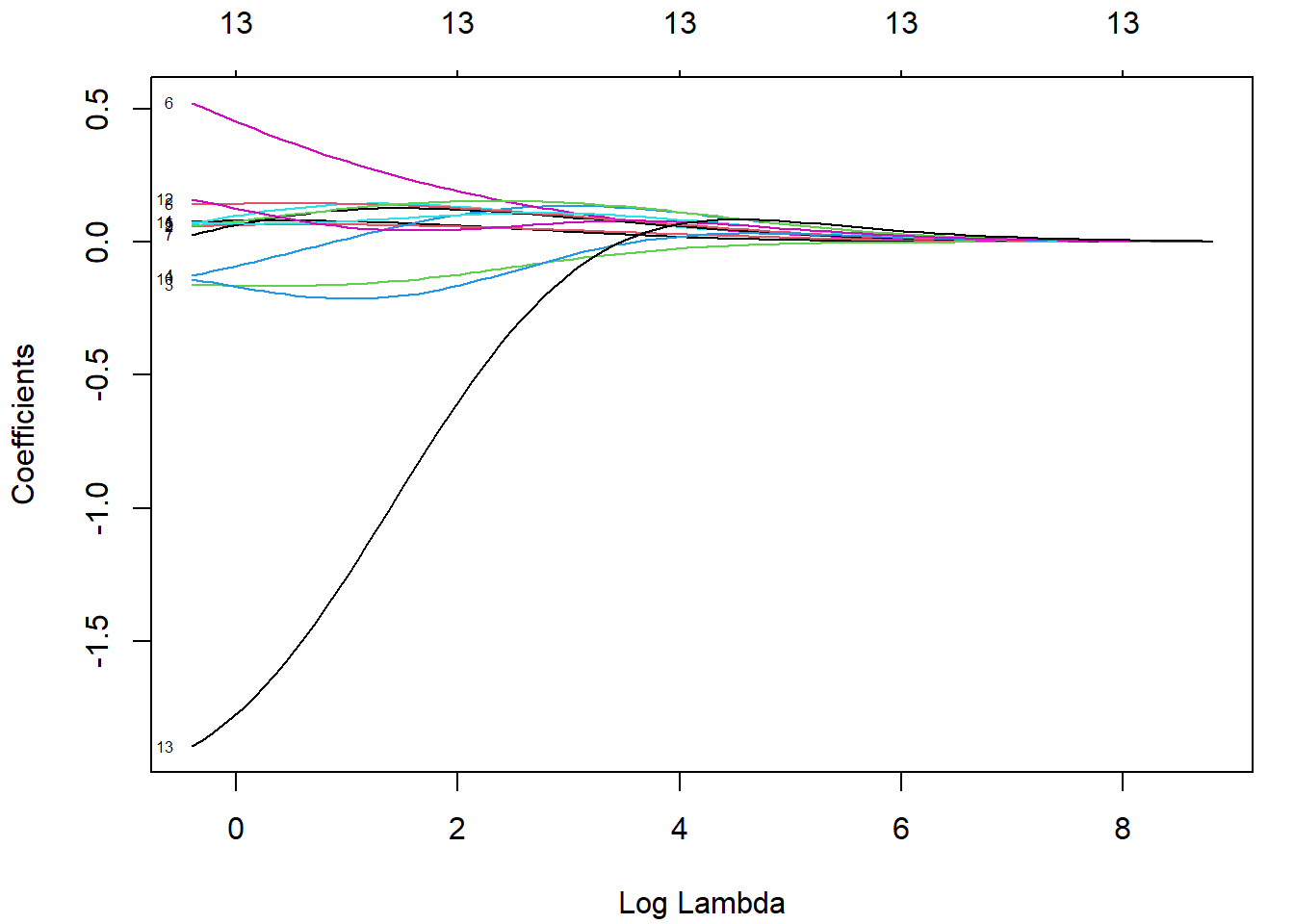
Figura 6.1: Gráfico de perfil de la evolución de los coeficientes en función del logaritmo de la penalización del ajuste ridge.
Podemos obtener el modelo o predicciones para un valor concreto de \(\lambda\):
coef(fit.ridge, s = 2) # lambda = 2## 14 x 1 sparse Matrix of class "dgCMatrix"
## s1
## (Intercept) -2.948568
## age 0.079808
## weight 0.066058
## height -0.163590
## neck -0.018690
## chest 0.135327
## abdomen 0.344659
## hip 0.110577
## thigh 0.145096
## knee 0.113076
## ankle -0.206822
## biceps 0.072182
## forearm 0.073053
## wrist -1.441640Para seleccionar el parámetro de penalización por validación cruzada, empleamos cv.glmnet() (normalmente emplearíamos esta función en lugar de glmnet()).
El correspondiente método plot() muestra la evolución de los errores de validación cruzada en función de la penalización, incluyendo las bandas de un error estándar de Breiman (ver Figura 6.2).
set.seed(1)
cv.ridge <- cv.glmnet(x, y, alpha = 0)
plot(cv.ridge)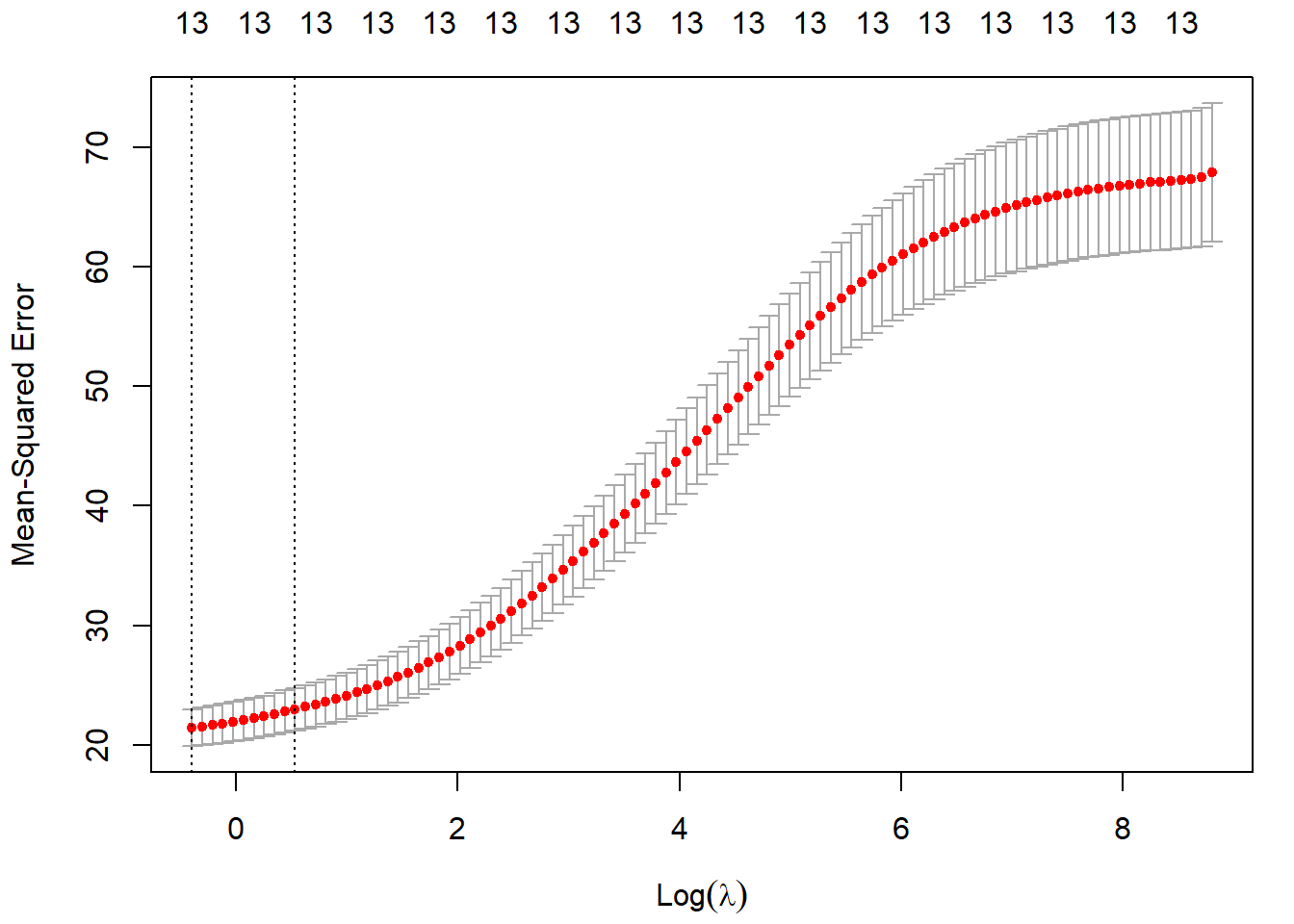
Figura 6.2: Error cuadrático medio de validación cruzada en función del logaritmo de la penalización del ajuste ridge, junto con los intervalos de un error estándar. Las líneas verticales se corresponden con lambda.min y lambda.1se.
En este caso el parámetro óptimo, según la regla de un error estándar de Breiman, sería56:
cv.ridge$lambda.1se## [1] 1.6984y el correspondiente modelo contiene todas las variables explicativas:
coef(cv.ridge) # s = "lambda.1se"## 14 x 1 sparse Matrix of class "dgCMatrix"
## s1
## (Intercept) -1.344135
## age 0.080359
## weight 0.066044
## height -0.164795
## neck -0.035658
## chest 0.129400
## abdomen 0.368416
## hip 0.102600
## thigh 0.145259
## knee 0.105121
## ankle -0.200403
## biceps 0.069859
## forearm 0.084012
## wrist -1.532999Finalmente, evaluamos la precisión en la muestra de test:
obs <- test$bodyfat
newx <- as.matrix(test[-1])
pred <- predict(cv.ridge, newx = newx) # s = "lambda.1se"
accuracy(pred, obs)## me rmse mae mpe mape r.squared
## 1.17762 4.42419 3.81770 -4.64274 24.66151 0.697436.1.3 Ejemplo: LASSO
Podemos ajustar modelos LASSO con la opción por defecto de glmnet() (alpha = 1, LASSO penalty).
Pero en este caso lo haremos al mismo tiempo que seleccionamos el parámetro de penalización por validación cruzada (ver Figura 6.3):
set.seed(1)
cv.lasso <- cv.glmnet(x,y)
plot(cv.lasso)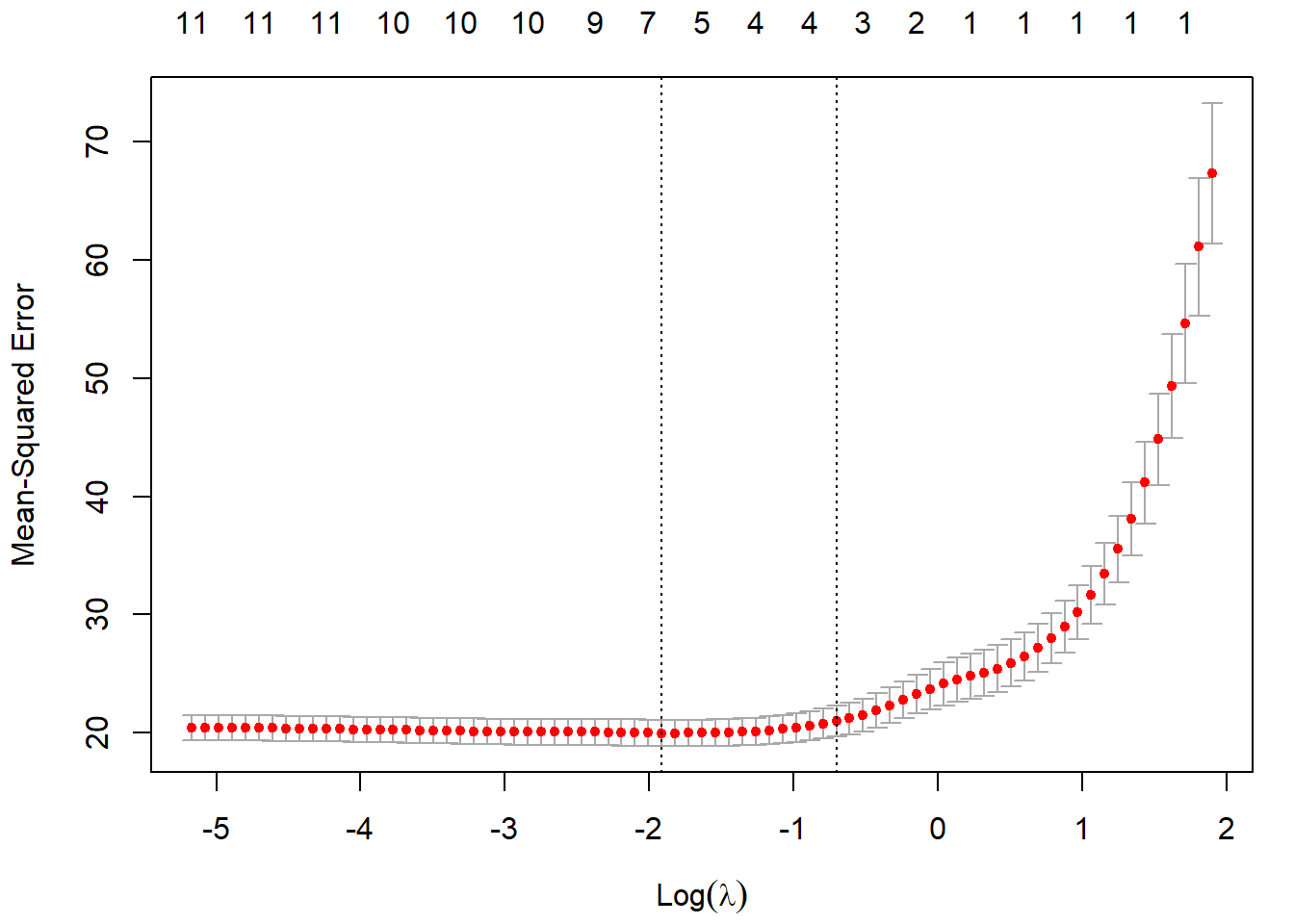
Figura 6.3: Error cuadrático medio de validación cruzada en función del logaritmo de la penalización del ajuste LASSO, junto con los intervalos de un error estándar. Las líneas verticales se corresponden con lambda.min y lambda.1se.
También podemos generar el gráfico con la evolución de los componentes a partir del ajuste almacenado en la componente $glmnet.fit:
plot(cv.lasso$glmnet.fit, xvar = "lambda", label = TRUE)
abline(v = log(cv.lasso$lambda.1se), lty = 2)
abline(v = log(cv.lasso$lambda.min), lty = 3)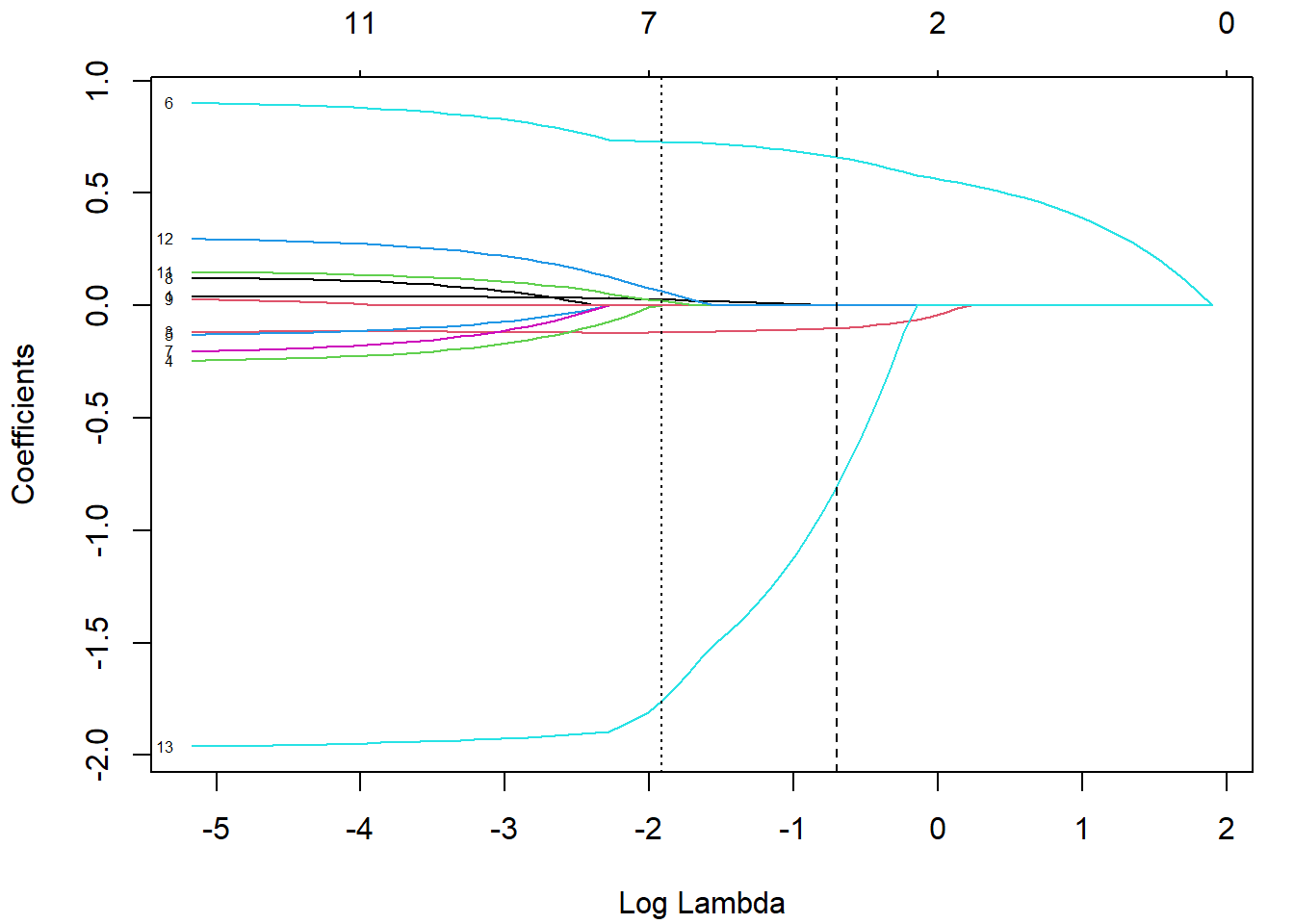
Figura 6.4: Evolución de los coeficientes en función del logaritmo de la penalización del ajuste LASSO. Las líneas verticales se corresponden con lambda.min y lambda.1se.
Como podemos observar en la Figura 6.4, la penalización LASSO tiende a forzar que las estimaciones de los coeficientes sean exactamente cero cuando el parámetro de penalización \(\lambda\) es suficientemente grande. En este caso, el modelo resultante (empleando la regla oneSE) solo contiene 3 variables explicativas:
coef(cv.lasso) # s = "lambda.1se"## 14 x 1 sparse Matrix of class "dgCMatrix"
## s1
## (Intercept) -9.58463
## age .
## weight .
## height -0.10060
## neck .
## chest .
## abdomen 0.66075
## hip .
## thigh .
## knee .
## ankle .
## biceps .
## forearm .
## wrist -0.80327Por tanto, este método también podría ser empleado para la selección de variables.
Si se quisiera ajustar el modelo sin regularización con estas variables, solo habría que establecer relax = TRUE en la llamada a glmnet() o cv.glmnet().
Finalmente, evaluamos también la precisión en la muestra de test:
pred <- predict(cv.lasso, newx = newx)
accuracy(pred, obs)## me rmse mae mpe mape r.squared
## 1.32227 4.29096 3.73005 -3.38653 23.84939 0.715386.1.4 Ejemplo: elastic net
Podemos ajustar modelos elastic net para un valor concreto de alpha empleando la función glmnet(), pero las opciones del paquete no incluyen la selección de este hiperparámetro.
Aunque se podría implementar fácilmente (como se muestra en help(cv.glmnet)), resulta mucho más cómodo emplear el método "glmnet" de caret:
library(caret)
modelLookup("glmnet") ## model parameter label forReg forClass probModel
## 1 glmnet alpha Mixing Percentage TRUE TRUE TRUE
## 2 glmnet lambda Regularization Parameter TRUE TRUE TRUEset.seed(1)
# Se podría emplear una fórmula: train(bodyfat ~ ., data = train, ...)
caret.glmnet <- train(x, y, method = "glmnet",
preProc = c("zv", "center", "scale"), tuneLength = 5,
trControl = trainControl(method = "cv", number = 5))
caret.glmnet## glmnet
##
## 196 samples
## 13 predictor
##
## Pre-processing: centered (13), scaled (13)
## Resampling: Cross-Validated (5 fold)
## Summary of sample sizes: 159, 157, 156, 156, 156
## Resampling results across tuning parameters:
##
## alpha lambda RMSE Rsquared MAE
## 0.100 0.0062187 4.4663 0.71359 3.6756
## 0.100 0.0288646 4.4595 0.71434 3.6741
## 0.100 0.1339777 4.4570 0.71443 3.6906
## 0.100 0.6218696 4.5473 0.70262 3.7527
## 0.100 2.8864628 4.9398 0.66058 4.0574
## 0.325 0.0062187 4.4646 0.71383 3.6735
## 0.325 0.0288646 4.4515 0.71542 3.6676
## 0.325 0.1339777 4.4547 0.71472 3.6885
## 0.325 0.6218696 4.5082 0.70919 3.7079
## 0.325 2.8864628 5.1988 0.63972 4.2495
## 0.550 0.0062187 4.4609 0.71432 3.6695
## 0.550 0.0288646 4.4459 0.71622 3.6637
## [ reached getOption("max.print") -- omitted 13 rows ]
##
## RMSE was used to select the optimal model using the smallest value.
## The final values used for the model were alpha = 1 and lambda = 0.13398.Los resultados de la selección de los hiperparámetros \(\alpha\) y \(\lambda\) de regularización se muestran en la Figura 6.5:
ggplot(caret.glmnet, highlight = TRUE)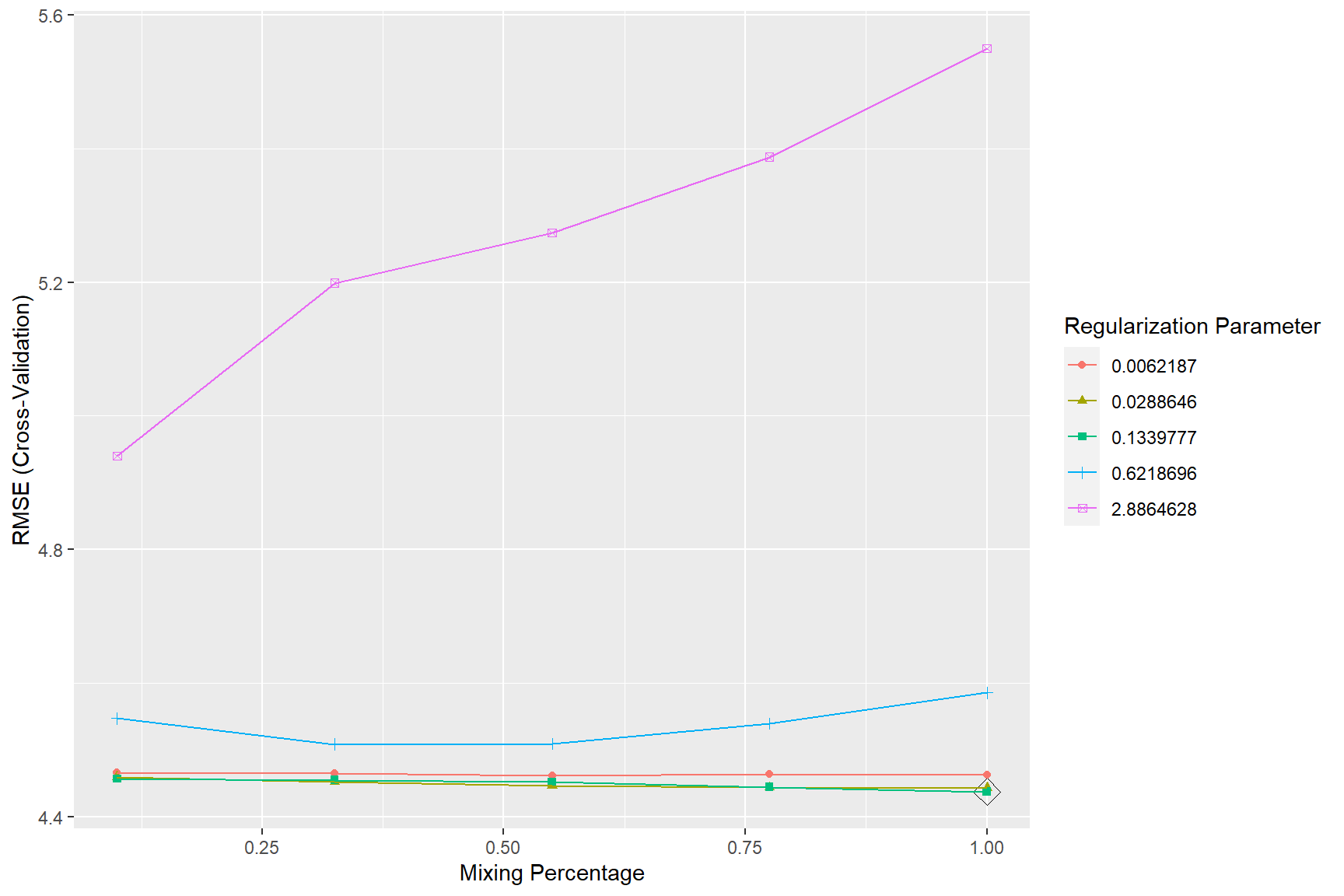
Figura 6.5: Errores RMSE de validación cruzada de los modelos elastic net en función de los hiperparámetros de regularización.
Finalmente, se evalúan las predicciones en la muestra de test del modelo ajustado (que en esta ocasión mejoran los resultados del modelo LASSO obtenido en la sección anterior):
pred <- predict(caret.glmnet, newdata = test)
accuracy(pred, obs)## me rmse mae mpe mape r.squared
## 1.36601 4.09331 3.50120 -1.25401 21.20872 0.74099Ejercicio 6.1 Continuando con el conjunto de datos mpae::bfan empleado en ejercicios de capítulos anteriores, particiona los datos y clasifica los individuos según su nivel de grasa corporal (bfan) mediante modelos logísticos:
Con penalización ridge, seleccionada mediante validación cruzada, empleando el paquete
glmnet.Con penalización LASSO, seleccionada mediante validación cruzada, empleando el paquete
glmnet.Con penalización elastic net, seleccionando los valores óptimos de los hiperparámetros, empleando
caret.Evalúa la precisión de las predicciones de los modelos en la muestra de test y compara los resultados.