1.3 Construcción y evaluación de los modelos

En inferencia estadística clásica el procedimiento habitual es emplear toda la información disponible para construir un modelo válido (que refleje de la forma más fiel posible lo que ocurre en la población) y, asumiendo que el modelo es el verdadero (lo que en general sería falso), utilizar resultados teóricos para evaluar su precisión. Por ejemplo, en el caso de regresión lineal múltiple, el coeficiente de determinación ajustado es una medida de la precisión del modelo para predecir nuevas observaciones (no se debe emplear el coeficiente de determinación sin ajustar; aunque, en cualquier caso, su validez depende de la de las suposiciones estructurales del modelo).

Alternativamente, en estadística computacional es habitual emplear técnicas de remuestreo para evaluar la precisión (entrenando también el modelo con todos los datos disponibles), principalmente validación cruzada (leave-one-out, k-fold), jackknife o bootstrap.

Por otra parte, como ya se comentó, algunos de los modelos empleados en AE son muy flexibles (están hiperparametrizados) y pueden aparecer problemas si se permite que se ajusten demasiado bien a las observaciones (podrían llegar a interpolar los datos). En estos casos habrá que controlar el procedimiento de aprendizaje, típicamente a través de parámetros relacionados con la complejidad del modelo (ver siguiente sección).

En AE se distingue entre parámetros estructurales, los que van a ser estimados al ajustar el modelo a los datos (en el entrenamiento), e hiperparámetros (tuning parameters o parámetros de ajuste), que imponen restricciones al aprendizaje del modelo (por ejemplo, determinando el número de parámetros estructurales). Si los hiperparámetros seleccionados producen un modelo demasiado complejo, aparecerán problemas de sobreajuste (overfitting), y en caso contrario, de infraajuste (undefitting).

Hay que tener en cuenta también que al aumentar la complejidad disminuye la interpretabilidad de los modelos. Se trata, por tanto, de conseguir buenas predicciones (habrá que evaluar la capacidad predictiva) con el modelo más sencillo posible.

1.3.1 Equilibrio entre sesgo y varianza: infraajuste y sobreajuste

La idea es que queremos aprender más allá de los datos empleados en el entrenamiento (en estadística diríamos que queremos hacer inferencia sobre nuevas observaciones). Como ya se comentó, en AE hay que tener especial cuidado con el sobreajuste. Este problema ocurre cuando el modelo se ajusta demasiado bien a los datos de entrenamiento, pero falla cuando se utiliza en un nuevo conjunto de datos (nunca antes visto).

Como ejemplo ilustrativo emplearemos regresión polinómica, considerando el grado del polinomio como un hiperparámetro que determina la complejidad del modelo. En primer lugar simulamos una muestra y ajustamos modelos polinómicos con distintos grados de complejidad.

# Simulación datos
n <- 30
x <- seq(0, 1, length = n)
mu <- 2 + 4*(5*x - 1)*(4*x - 2)*(x - 0.8)^2 # grado 4
sd <- 0.5
set.seed(1)
y <- mu + rnorm(n, 0, sd)
plot(x, y) 
lines(x, mu, lwd = 2)
# Ajuste de los modelos
fit1 <- lm(y ~ x)
lines(x, fitted(fit1))
fit2 <- lm(y ~ poly(x, 4))
lines(x, fitted(fit2), lty = 2)
fit3 <- lm(y ~ poly(x, 20)) 
lines(x, fitted(fit3), lty = 3)
legend("topright", lty = c(1, 1, 2, 3), lwd = c(2, 1, 1, 1),
       legend = c("Verdadero", "Ajuste con grado 1",
                  "Ajuste con grado 4", "Ajuste con grado 20"))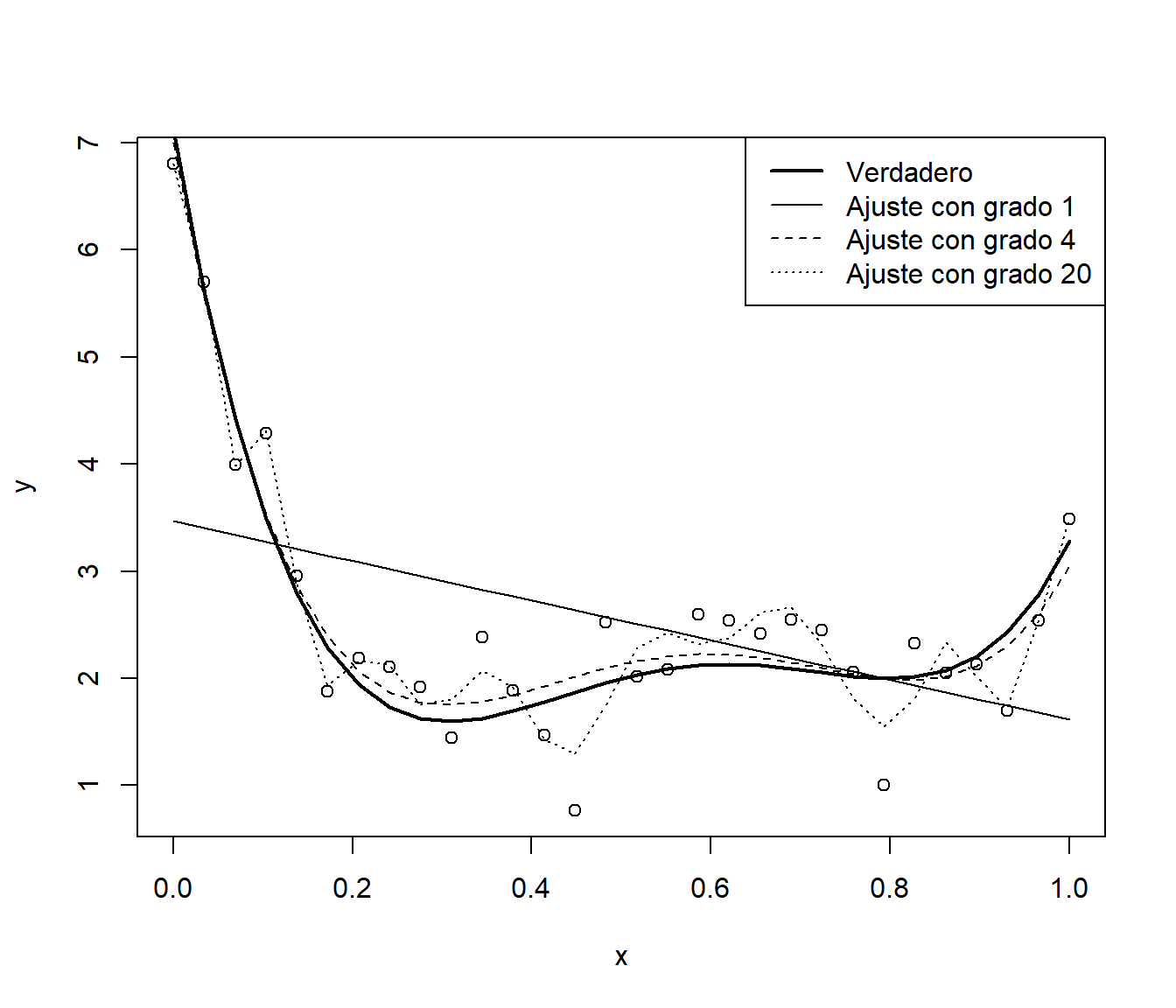

Figura 1.3: Muestra (simulada) y ajustes polinómicos con distinta complejidad.

Como se observa en la Figura 1.3, al aumentar la complejidad del modelo se consigue un mejor ajuste a los datos observados (usados para el entrenamiento), a costa de un incremento en la variabilidad de las predicciones, lo que puede producir un mal comportamiento del modelo al ser empleado en un conjunto de datos distinto del observado.

Si calculamos medidas de bondad de ajuste, como el error cuadrático medio (mean squared error, MSE) o el coeficiente de determinación (\(R^2\)), se obtienen mejores resultados al aumentar la complejidad. Como se trata de modelos lineales, podríamos obtener también el coeficiente de determinación ajustado (\(R^2_{adj}\)), que sería preferible (en principio, ya que dependería de la validez de las hipótesis estructurales del modelo) para medir la precisión al emplear los modelos en un nuevo conjunto de datos (ver Tabla 1.1).

sapply(list(fit1 = fit1, fit2 = fit2, fit3 = fit3),
       function(x) with(summary(x),
          c(MSE = mean(residuals^2), R2 = r.squared, R2adj = adj.r.squared)))

Tabla 1.1: Medidas de bondad de ajuste de los modelos polinómicos (obtenidas a partir de la muestra de entrenamiento).

	\(MSE\)	\(R^2\)	\(R^2_{adj}\)
fit1	1.22	0.20	0.17
fit2	0.19	0.87	0.85
fit3	0.07	0.95	0.84

Por ejemplo, si generamos nuevas respuestas de este proceso, la precisión del modelo más complejo empeorará considerablemente (ver Figura 1.4):

y.new <- mu + rnorm(n, 0, sd)
plot(x, y) 
points(x, y.new, pch = 2)
lines(x, mu, lwd = 2)
lines(x, fitted(fit1))
lines(x, fitted(fit2), lty = 2)
lines(x, fitted(fit3), lty = 3)
leyenda <- c("Verdadero", "Muestra", "Ajuste con grado 1",
       "Ajuste con grado 4", "Ajuste con grado 20", "Nuevas observaciones")
legend("topright", legend = leyenda, lty = c(1, NA, 1, 2, 3, NA),
       lwd = c(2, NA, 1, 1, 1, NA), pch = c(NA, 1, NA, NA, NA, 2))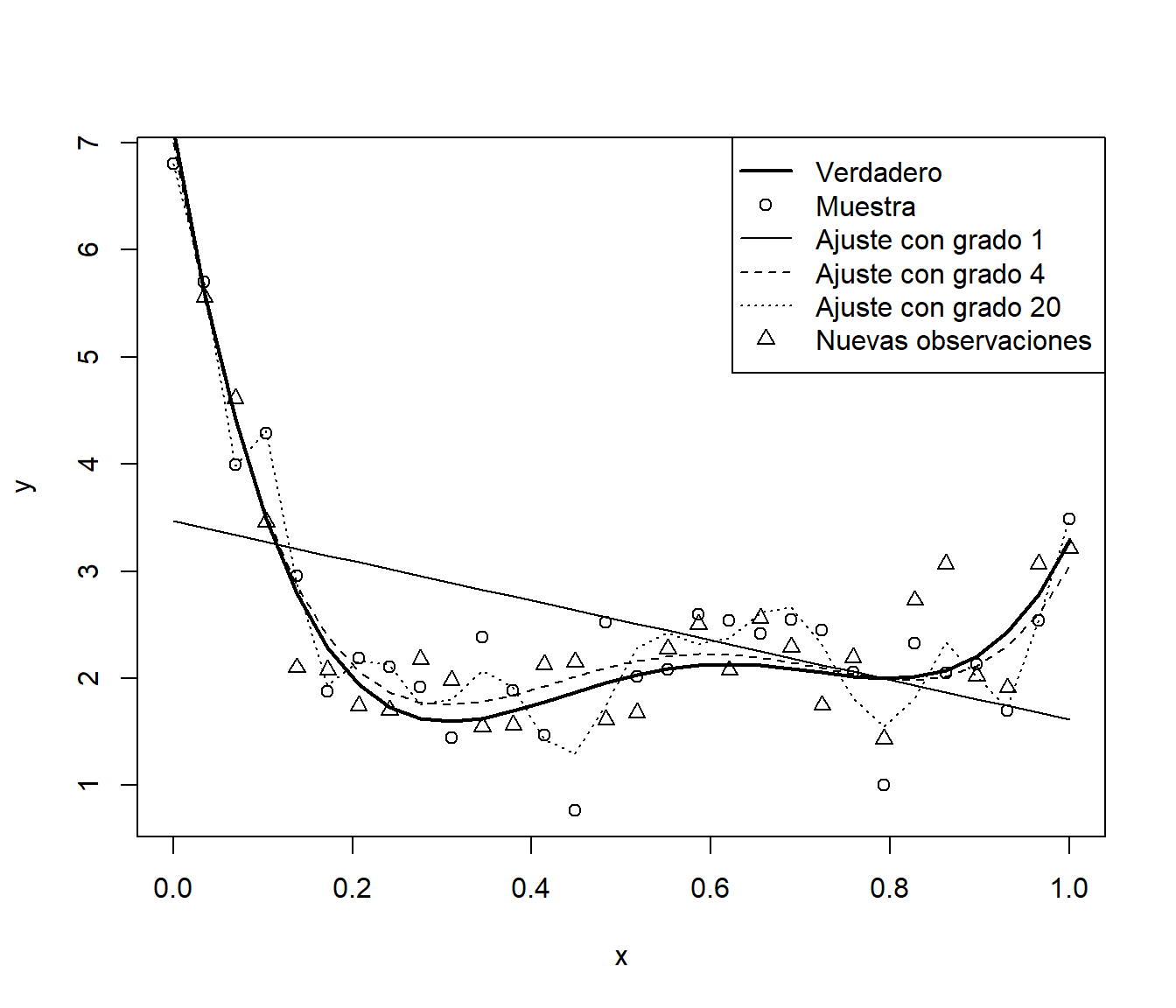

Figura 1.4: Muestra con ajustes polinómicos con distinta complejidad y nuevas observaciones.

MSEP <- sapply(list(fit1 = fit1, fit2 = fit2, fit3 = fit3), 
               function(x) mean((y.new - fitted(x))^2))
MSEP

##    fit1    fit2    fit3 
## 1.49832 0.17112 0.26211

Como ejemplo adicional, para evitar el efecto de la aleatoriedad de la muestra, en el siguiente código se simulan 100 muestras del proceso anterior a las que se les ajustan modelos polinómicos variando el grado desde 1 hasta 20. Posteriormente se evalúa la precisión, en la muestra empleada en el ajuste y en un nuevo conjunto de datos procedente de la misma población.

nsim <- 100
set.seed(1)
grado.max <- 20
grados <- seq_len(grado.max) 
# Simulación, ajustes y errores cuadráticos
mse <- mse.new <- matrix(nrow = grado.max, ncol = nsim) 
for(i in seq_len(nsim)) {
  y <- mu + rnorm(n, 0, sd)
  y.new <- mu + rnorm(n, 0, sd)
  for (grado in grados) { # grado <- 1
    fit <- lm(y ~ poly(x, grado))
    mse[grado, i] <- mean(residuals(fit)^2)
    mse.new[grado, i] <- mean((y.new - fitted(fit))^2)
  }
}
# Representación errores simulaciones
matplot(grados, mse, type = "l", col = "lightgray", lty = 1, ylim = c(0, 2),
  xlab = "Grado del polinomio (complejidad)", ylab = "Error cuadrático medio")
matlines(grados, mse.new, type = "l", lty = 2, col = "lightgray") 
# Errores globales
precision <- rowMeans(mse)
precision.new <- rowMeans(mse.new)
lines(grados, precision, lwd = 2)
lines(grados, precision.new, lty = 2, lwd = 2)
abline(h = sd^2, lty = 3);abline(v = 4, lty = 3)
leyenda <-  c("Muestras", "Nuevas observaciones")
legend("topright", legend = leyenda, lty = c(1, 2))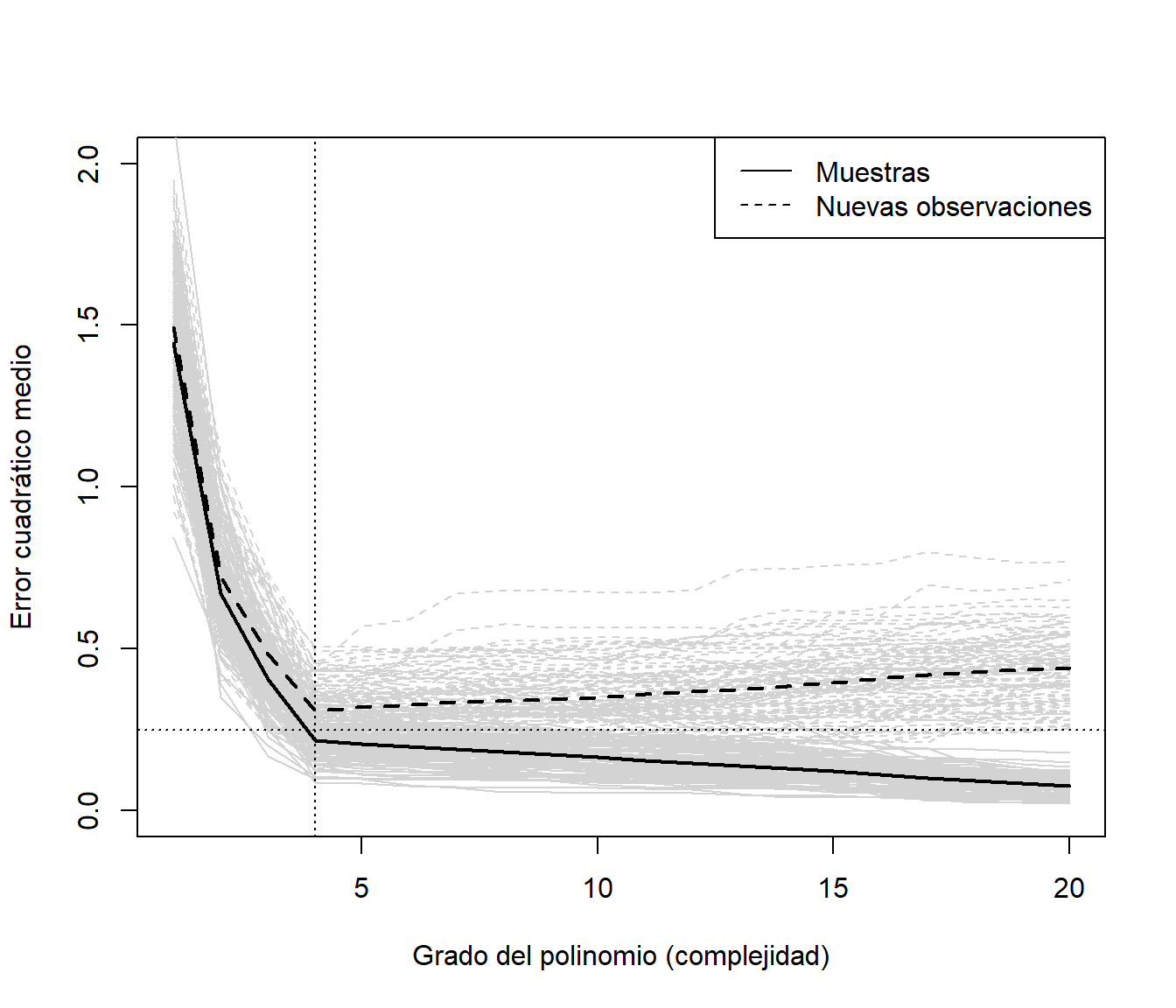

Figura 1.5: Precisiones (errores cuadráticos medios) de ajustes polinómicos variando la complejidad, en las muestras empleadas en el ajuste y en nuevas observaciones (simulados).

Como se puede observar en la Figura 1.5, los errores de entrenamiento disminuyen a medida que aumenta la complejidad del modelo. Sin embargo, los errores de predicción en nuevas observaciones inicialmente disminuyen, hasta alcanzar un mínimo marcado por la línea de puntos vertical, que se corresponde con el modelo de grado 4, y posteriormente aumentan (la línea de puntos horizontal es la varianza del proceso; el error cuadrático medio de predicción asintótico). La línea vertical representa el equilibrio entre el sesgo y la varianza. Considerando un valor de complejidad a la izquierda de esa línea tendríamos infraajuste (mayor sesgo y menor varianza), y a la derecha, sobreajuste (menor sesgo y mayor varianza).

Desde un punto de vista más formal, considerando el modelo (1.1) y una función de pérdidas cuadrática, el predictor óptimo (desconocido) sería la media condicional \(m(\mathbf{x}) = E\left( \left. Y\right\vert \mathbf{X}=\mathbf{x} \right)\)¹⁰. Por tanto, los predictores serían realmente estimaciones de la función de regresión, \(\hat Y(\mathbf{x}) = \hat m(\mathbf{x})\), y podemos expresar la media del error cuadrático de predicción en términos del sesgo y la varianza: \[ \begin{aligned} E \left( Y(\mathbf{x}_0) - \hat Y(\mathbf{x}_0) \right)^2 & = E \left( m(\mathbf{x}_0) + \varepsilon - \hat m(\mathbf{x}_0) \right)^2 = E \left( m(\mathbf{x}_0) - \hat m(\mathbf{x}_0) \right)^2 + \sigma^2 \\ & = E^2 \left( m(\mathbf{x}_0) - \hat m(\mathbf{x}_0) \right) + Var\left( \hat m(\mathbf{x}_0) \right) + \sigma^2 \\ & = \text{sesgo}^2 + \text{varianza} + \text{error irreducible} \end{aligned} \] donde \(\mathbf{x}_0\) hace referencia al vector de valores de las variables explicativas de una nueva observación (no empleada en la construcción del predictor).

En general, al aumentar la complejidad disminuye el sesgo y aumenta la varianza (y viceversa). Esto es lo que se conoce como el dilema o compromiso entre el sesgo y la varianza (bias-variance tradeoff). La recomendación sería por tanto seleccionar los hiperparámetros (el modelo final) tratando de que haya un equilibrio entre el sesgo y la varianza (ver Figura 1.6).

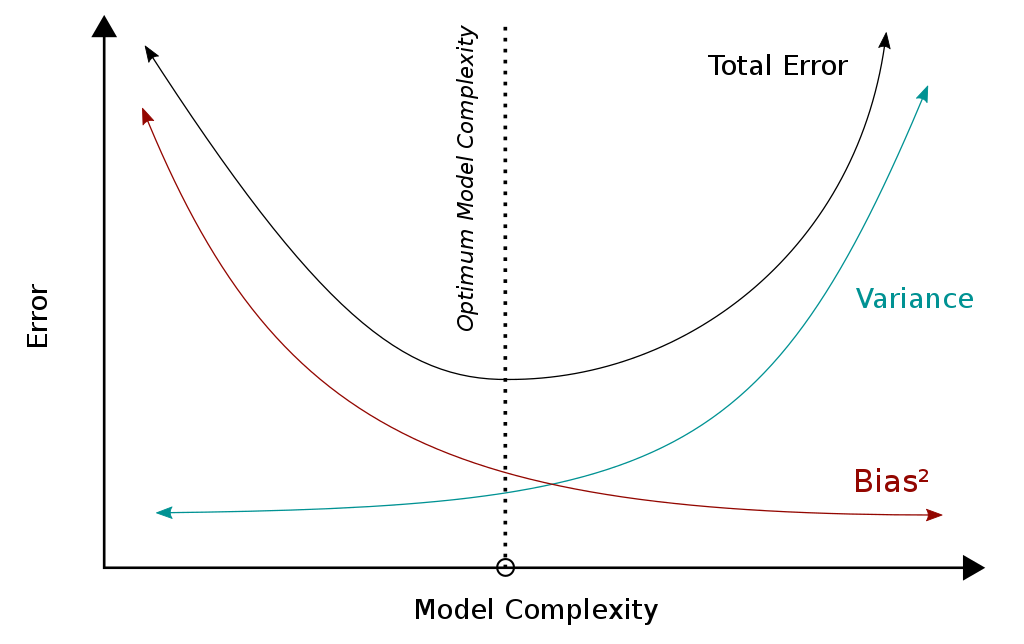
Figura 1.6: Equilibrio entre sesgo y varianza (Fuente: Wikimedia Commons).

1.3.2 Datos de entrenamiento y datos de test

Como se mostró en la sección anterior, hay que tener mucho cuidado si se pretende evaluar la precisión de las predicciones empleando la muestra de entrenamiento. Si el número de observaciones no es muy grande, se puede entrenar el modelo con todos los datos y emplear técnicas de remuestreo para evaluar la precisión (típicamente validación cruzada o bootstrap). Aunque habría que asegurarse de que el procedimiento de remuestreo empleado es adecuado (por ejemplo, la presencia de dependencia requeriría de métodos más sofisticados).

Sin embargo, si el número de observaciones es grande, se suele emplear el procedimiento tradicional en ML, que consiste en particionar la base de datos en 2 (o incluso en 3) conjuntos (disjuntos):

• Conjunto de datos de entrenamiento (o aprendizaje) para construir los modelos.

• Conjunto de datos de test para evaluar el rendimiento de los modelos (los errores observados en esta muestra servirán para aproximar lo que ocurriría con nuevas observaciones).

Típicamente se selecciona al azar el 80 % de los datos como muestra de entrenamiento y el 20 % restante como muestra de test, aunque esto dependería del número de datos (los resultados serán aleatorios y su variabilidad dependerá principalmente del tamaño de las muestras). En R se puede realizar el particionamiento de los datos empleando la función sample() del paquete base (otra alternativa sería emplear la función createDataPartition() del paquete caret, como se describe en la Sección 1.6).

Como ejemplo consideraremos el conjunto de datos Boston del paquete MASS (Ripley, 2023) que contiene, entre otros datos, la valoración de las viviendas (medv, mediana de los valores de las viviendas ocupadas, en miles de dólares) y el porcentaje de población con “menor estatus” (lstat) en los suburbios de Boston. Podemos construir las muestras de entrenamiento (80 %) y de test (20 %) con el siguiente código:

data(Boston, package = "MASS")
set.seed(1)
nobs <- nrow(Boston)
itrain <- sample(nobs, 0.8 * nobs)
train <- Boston[itrain, ]
test <- Boston[-itrain, ]

Los datos de test deberían utilizarse únicamente para evaluar los modelos finales, no se deberían emplear para seleccionar hiperparámetros. Para seleccionarlos se podría volver a particionar los datos de entrenamiento, es decir, dividir la muestra en tres subconjuntos: datos de entrenamiento, de validación y de test (por ejemplo considerando un 70 %, 15 % y 15 % de las observaciones, respectivamente). Para cada combinación de hiperparámetros se ajustaría el correspondiente modelo con los datos de entrenamiento, se emplearían los de validación para evaluarlos y posteriormente seleccionar los valores “óptimos”. Por último, se emplean los datos de test para evaluar el rendimiento del modelo seleccionado. No obstante, lo más habitual es seleccionar los hiperparámetros empleando validación cruzada (u otro tipo de remuestreo) en la muestra de entrenamiento, en lugar de considerar una muestra adicional de validación. En la siguiente sección se tratará esta última aproximación. En la Sección 4.1 (Bagging) se describirá cómo usar remuestreo para evaluar la precisión de las predicciones y su aplicación para la selección de hiperparámetros.

1.3.3 Selección de hiperparámetros mediante validación cruzada

Como se mencionó anteriormente, una herramienta para evaluar la calidad predictiva de un modelo es la validación cruzada (CV, cross-validation), que permite cuantificar el error de predicción utilizando una única muestra de datos. En su versión más simple, validación cruzada dejando uno fuera (leave-one-out cross-validation, LOOCV), para cada observación de la muestra se realiza un ajuste empleando el resto de las observaciones, y se mide el error de predicción en esa observación (único dato no utilizado en el ajuste del modelo). Finalmente, combinando todos los errores individuales se pueden obtener medidas globales del error de predicción (o aproximar otras características de su distribución).

El método de LOOCV requeriría, en principio (ver comentarios más adelante), el ajuste de un modelo para cada observación, por lo que pueden aparecer problemas computacionales si el conjunto de datos es grande. En este caso se suelen emplear grupos de observaciones en lugar de observaciones individuales. Si se particiona el conjunto de datos en k grupos, típicamente 10 o 5 grupos, se denomina k-fold cross-validation (LOOCV sería un caso particular considerando un número de grupos igual al número de observaciones)¹¹. Hay muchas variaciones de este método, entre ellas particionar repetidamente de forma aleatoria los datos en un conjunto de entrenamiento y otro de validación (de esta forma, algunas observaciones podrían aparecer repetidas varias veces y otras ninguna en las muestras de validación).

Continuando con el ejemplo anterior, supongamos que queremos emplear regresión polinómica para explicar la valoración de las viviendas a partir del “estatus” de los residentes (ver Figura 1.7). Al igual que se hizo en la Sección 1.3.1, consideraremos el grado del polinomio como un hiperparámetro.

plot(medv ~ lstat, data = train)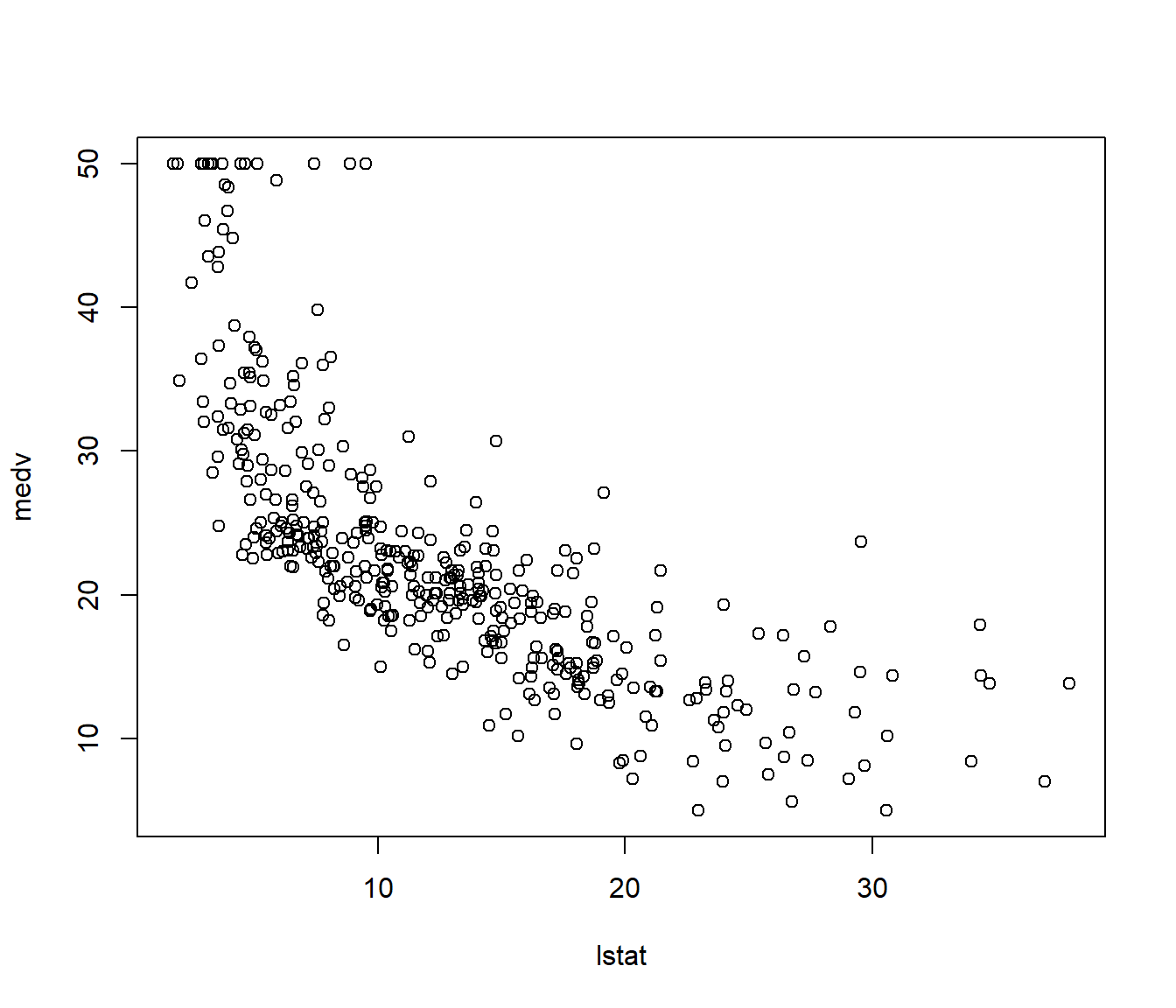

Figura 1.7: Gráfico de dispersión de las valoraciones de las viviendas (medv) frente al porcentaje de población con “menor estatus” (lstat).

Podríamos emplear la siguiente función que devuelve para cada observación (fila) de una muestra de entrenamiento, el error de predicción en esa observación ajustando un modelo lineal con todas las demás observaciones:

cv.lm0 <- function(formula, datos) {
    respuesta <- as.character(formula)[2] # extraer nombre variable respuesta
    n <- nrow(datos)
    cv.res <- numeric(n)
    for (i in 1:n) {
        modelo <- lm(formula, datos[-i, ])
        cv.pred <- predict(modelo, newdata = datos[i, ])
        cv.res[i] <- cv.pred - datos[i, respuesta]
    }
    return(cv.res)
}

La función anterior no es muy eficiente, pero se podría modificar fácilmente para otros métodos de regresión¹². En el caso de regresión lineal múltiple (y de otros predictores lineales), se pueden obtener fácilmente las predicciones eliminando una de las observaciones a partir del ajuste con todos los datos. Por ejemplo, en lugar de la anterior, sería preferible emplear la siguiente función (consultar la ayuda de rstandard()):

cv.lm <- function(formula, datos) {
    modelo <- lm(formula, datos)
    return(rstandard(modelo, type = "predictive"))
}

Empleando esta función, podemos calcular una medida del error de predicción de validación cruzada (en este caso el error cuadrático medio) para cada valor del hiperparámetro (grado del ajuste polinómico) y seleccionar el que lo minimiza (ver Figura 1.8).

grado.max <- 10
grados <- seq_len(grado.max) 
cv.mse <- cv.mse.sd <- numeric(grado.max)
for(grado in grados){
  # Tiempo de computación elevado!
  # cv.res <- cv.lm0(medv ~ poly(lstat, grado), train) 
  cv.res <- cv.lm(medv ~ poly(lstat, grado), train)
  se <- cv.res^2
  cv.mse[grado] <- mean(se)
  cv.mse.sd[grado] <- sd(se)/sqrt(length(se))
}
plot(grados, cv.mse, ylim = c(25, 45), xlab = "Grado del polinomio")
# Valor óptimo
imin.mse <- which.min(cv.mse)
grado.min <- grados[imin.mse]
points(grado.min, cv.mse[imin.mse], pch = 16)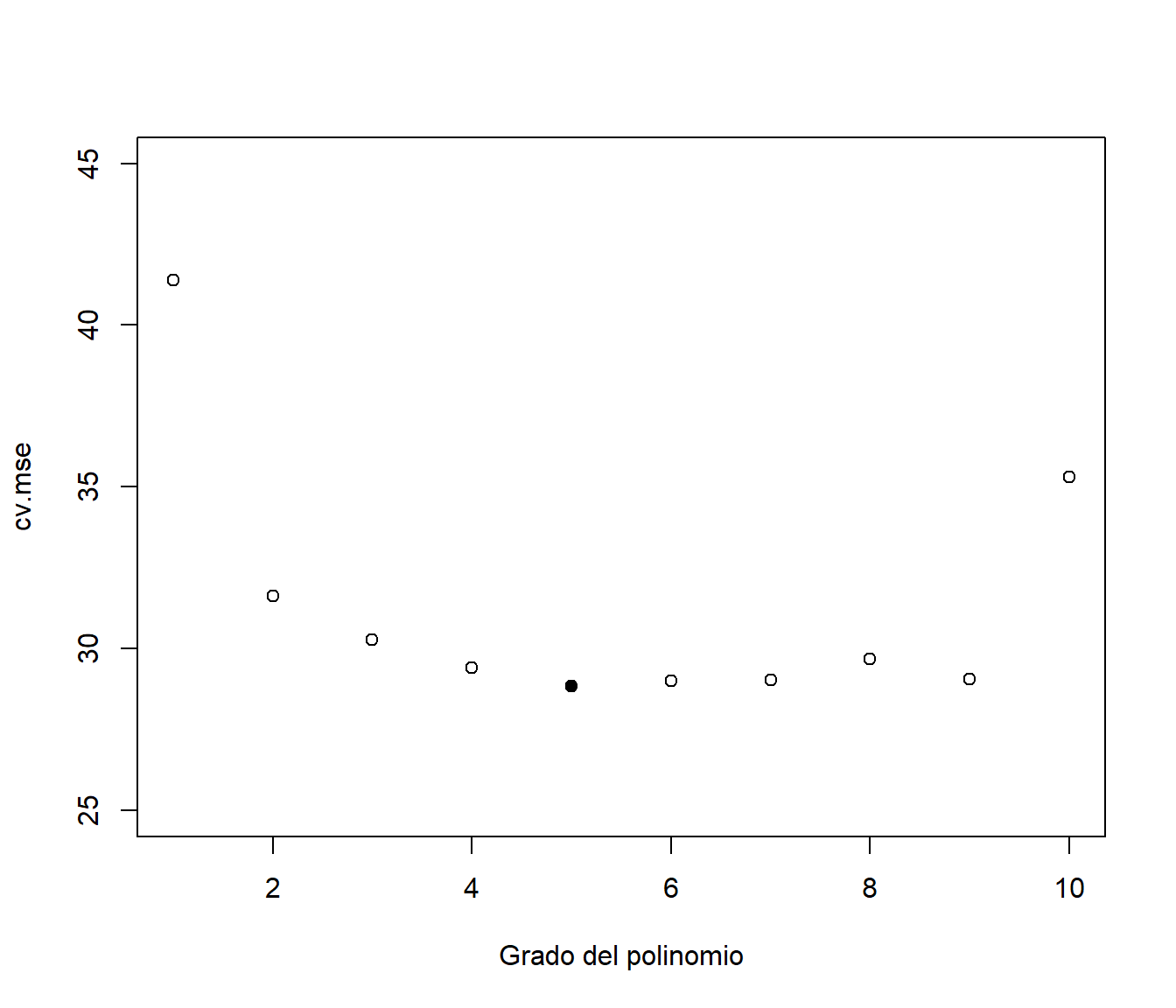

Figura 1.8: Error cuadrático medio de validación cruzada dependiendo del grado del polinomio (complejidad) y valor seleccionado con el criterio de un error estándar (punto sólido).

grado.min

## [1] 5

En lugar de emplear los valores óptimos de los hiperparámetros, Breiman et al. (1984) propusieron la regla de “un error estándar” para seleccionar la complejidad del modelo. La idea es que estamos trabajando con estimaciones de la precisión y pueden presentar variabilidad (si cambiamos la muestra o cambiamos la partición, los resultados seguramente cambiarán), por lo que la sugerencia es seleccionar el modelo más simple¹³ dentro de un error estándar de la precisión del modelo correspondiente al valor óptimo (se consideraría que no hay diferencias significativas en la precisión; además, se mitigaría el efecto de la variabilidad debida a aleatoriedad, incluyendo la inducida por la elección de la semilla; ver figuras 1.9 y 1.10).

plot(grados, cv.mse, ylim = c(25, 45),
  xlab = "Grado del polinomio")
segments(grados, cv.mse - cv.mse.sd, grados, cv.mse + cv.mse.sd)
# Límite superior "oneSE rule" 
upper.cv.mse <- cv.mse[imin.mse] + cv.mse.sd[imin.mse]
abline(h = upper.cv.mse, lty = 2)
# Complejidad mínima por debajo del límite
imin.1se <- min(which(cv.mse <= upper.cv.mse))
grado.1se <- grados[imin.1se]
points(grado.1se, cv.mse[imin.1se], pch = 16)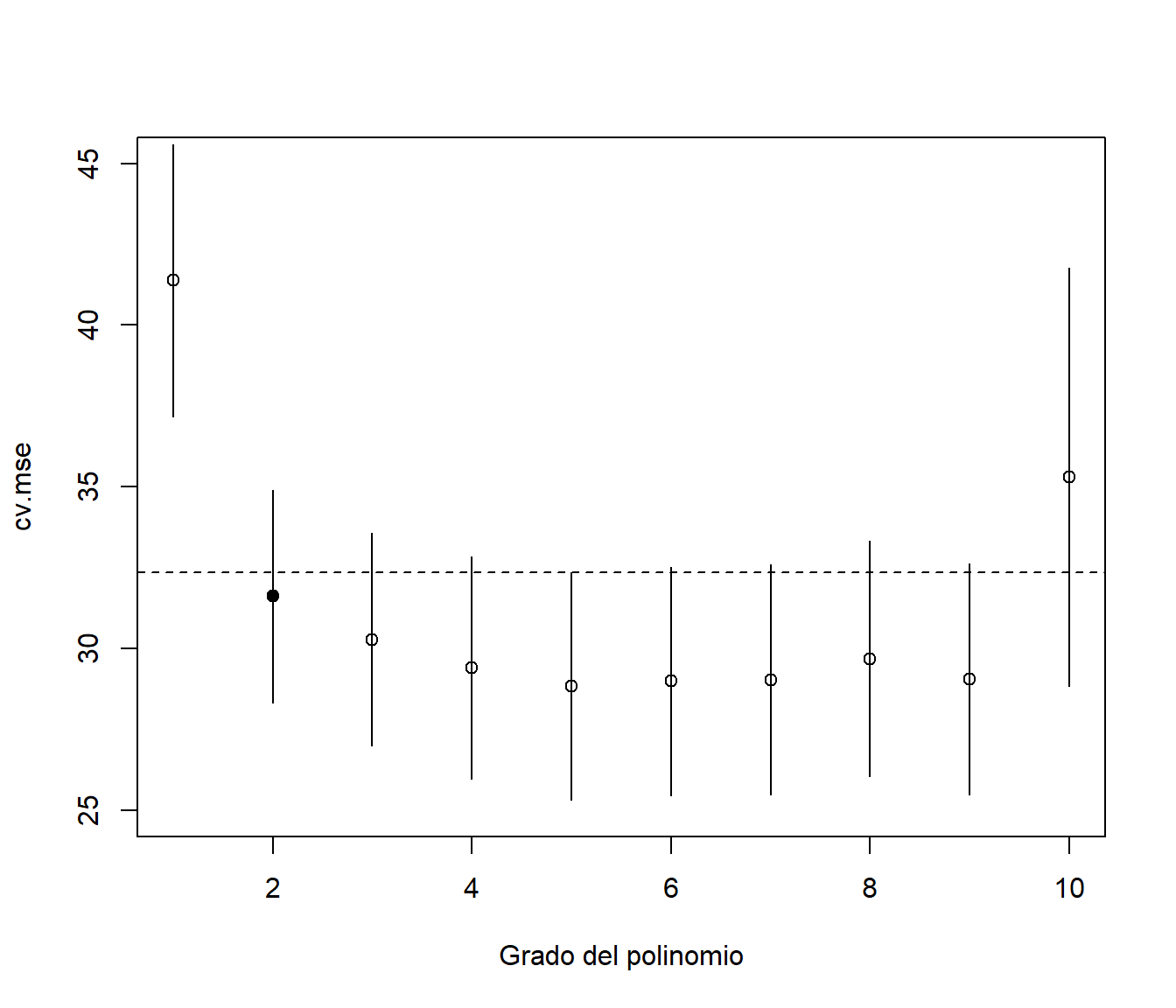

Figura 1.9: Error cuadrático medio de validación cruzada dependiendo del grado del polinomio (complejidad) y valor seleccionado con el criterio de un error estándar (punto sólido).

grado.1se

## [1] 2

plot(medv ~ lstat, data = train)
fit.min <- lm(medv ~ poly(lstat, grado.min), train)
fit.1se <- lm(medv ~ poly(lstat, grado.1se), train)
newdata <- data.frame(lstat = seq(0, 40, len = 100))
lines(newdata$lstat, predict(fit.min, newdata = newdata))
lines(newdata$lstat, predict(fit.1se, newdata = newdata), lty = 2)
legend("topright", legend = c(paste("Grado óptimo:", grado.min), 
       paste("oneSE rule:", grado.1se)), lty = c(1, 2))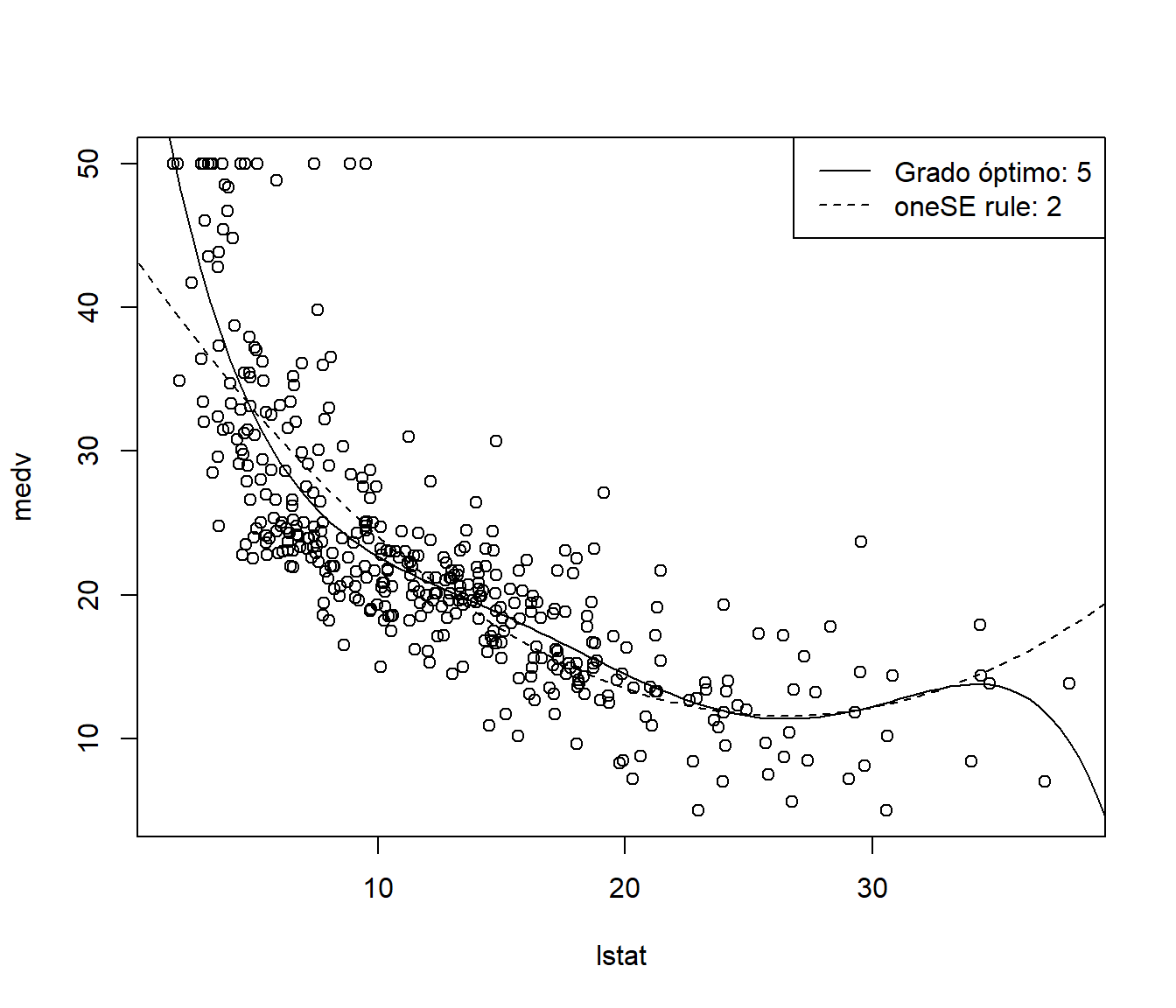

Figura 1.10: Ajuste de los modelos finales, empleando el valor óptimo (línea continua) y el criterio de un error estándar (línea discontinua) para seleccionar el grado del polinomio mediante validación cruzada.

Es importante destacar que la selección aleatoria puede no ser muy adecuada en el caso de dependencia, por ejemplo, para series de tiempo. En este caso se suele emplear el denominado rolling forecasting, considerando las observaciones finales como conjunto de validación, y para predecir en cada una de ellas se ajusta el modelo considerando únicamente observaciones anteriores (para más detalles, ver por ejemplo la Sección 5.10 de Hyndman y Athanasopoulos, 2021).

1.3.4 Evaluación de un método de regresión

Para estudiar la precisión de las predicciones de un método de regresión se evalúa el modelo en el conjunto de datos de test y se comparan las predicciones frente a los valores reales. Los resultados servirán como medidas globales de la calidad de las predicciones con nuevas observaciones.

obs <- test$medv
pred <- predict(fit.min, newdata = test)

Si generamos un gráfico de dispersión de observaciones frente a predicciones¹⁴, los puntos deberían estar en torno a la recta \(y=x\) (ver Figura 1.11).

plot(pred, obs, xlab = "Predicción", ylab = "Observado")
abline(a = 0, b = 1)
res <- lm(obs ~ pred)
# summary(res)
abline(res, lty = 2)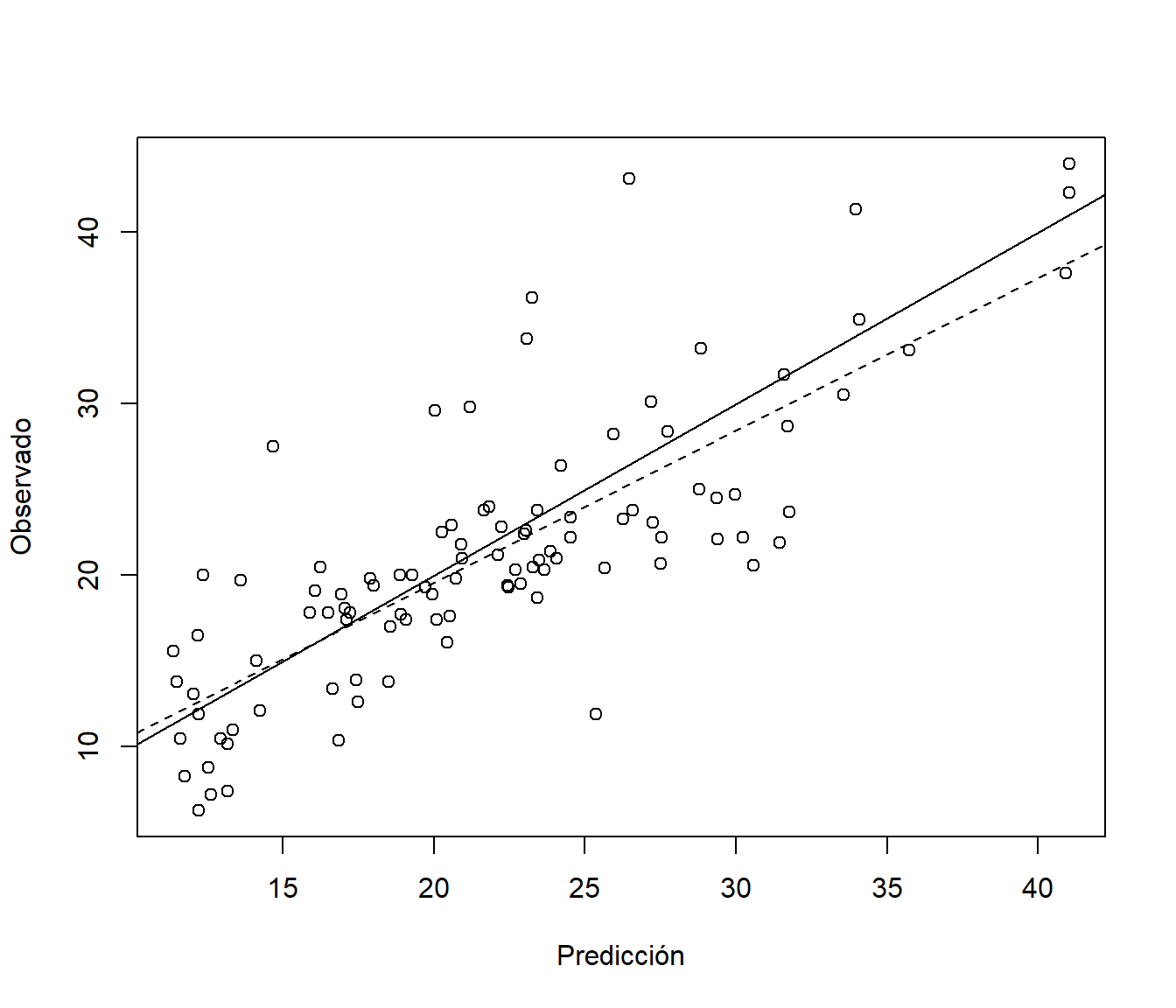

Figura 1.11: Gráfico de dispersión de observaciones frente a predicciones (incluyendo la identidad, línea continua, y el ajuste lineal, línea discontinua).

Este gráfico está implementado en la función pred.plot() del paquete mpae (aunque por defecto añade el suavizado robusto lowess(pred, obs)).

También es habitual calcular distintas medidas de error. Por ejemplo, podríamos emplear la función postResample() del paquete caret:

caret::postResample(pred, obs)

##     RMSE Rsquared      MAE 
##  4.85267  0.62596  3.66718

La función anterior, además de las medidas de error habituales (que dependen en su mayoría de la escala de la variable respuesta), calcula un pseudo R-cuadrado. En este paquete (y en muchos otros, como tidymodels o rattle) se emplea uno de los más utilizados, el cuadrado del coeficiente de correlación entre las predicciones y los valores observados (que se corresponde con la línea discontinua en la Figura 1.11). Su valor se suele interpretar como el del coeficiente de determinación en regresión lineal (aunque únicamente es una medida de correlación), y sería deseable que su valor fuese próximo a 1. Hay otras alternativas (ver Kvålseth, 1985), pero la idea es que deberían medir la proporción de variabilidad de la respuesta (en nuevas observaciones) explicada por el modelo, algo que en general no es cierto con el anterior¹⁵. La recomendación sería utilizar: \[\tilde R^2 = 1 - \frac{\sum_{i=1}^n(y_i - \hat y_i)^2}{\sum_{i=1}^n(y_i - \bar y)^2}\] (que sería una medida equivalente al coeficiente de determinación ajustado en regresión múltiple, pero sin depender de hipótesis estructurales del modelo), implementado junto con otras medidas en la siguiente función (incluida en el paquete mpae):

accuracy <- function(pred, obs, na.rm = FALSE, 
                     tol = sqrt(.Machine$double.eps)) {
  err <- obs - pred     # Errores
  if(na.rm) {
    is.a <- !is.na(err)
    err <- err[is.a]
    obs <- obs[is.a]
  }  
  perr <- 100*err/pmax(obs, tol)  # Errores porcentuales
  return(c(
    me = mean(err),           # Error medio
    rmse = sqrt(mean(err^2)), # Raíz del error cuadrático medio 
    mae = mean(abs(err)),     # Error absoluto medio
    mpe = mean(perr),         # Error porcentual medio
    mape = mean(abs(perr)),   # Error porcentual absoluto medio
    r.squared = 1 - sum(err^2)/sum((obs - mean(obs))^2) # Pseudo R-cuadrado
  ))
}
accu.min <- accuracy(pred, obs)
accu.min

##        me      rmse       mae       mpe      mape r.squared 
##  -0.67313   4.85267   3.66718  -8.23225  19.70974   0.60867

accu.1se <- accuracy(predict(fit.1se, newdata = test), obs)
accu.1se

##        me      rmse       mae       mpe      mape r.squared 
##  -0.92363   5.27974   4.12521  -9.00298  21.65124   0.53676

En este caso concreto (con la semilla establecida anteriormente), estimaríamos que el ajuste polinómico con el grado óptimo (seleccionado al minimizar el error cuadrático medio de validación cruzada) explicaría un 60.9 % de la variabilidad de la respuesta en nuevas observaciones (un 7.2 % más que el modelo seleccionado con el criterio de un error estándar de Breiman).

Ejercicio 1.1 Considerando de nuevo el ejemplo anterior, particiona la muestra en datos de entrenamiento (70 %), de validación (15 %) y de test (15 %), para entrenar los modelos polinómicos, seleccionar el grado óptimo (el hiperparámetro) y evaluar las predicciones del modelo final, respectivamente.

Podría ser de utilidad el siguiente código (basado en la aproximación de rattle), que particiona los datos suponiendo que están almacenados en el data.frame df:

df <- Boston
set.seed(1)
nobs <- nrow(df)
itrain <- sample(nobs, 0.7 * nobs)
inotrain <- setdiff(seq_len(nobs), itrain)
ivalidate <- sample(inotrain, 0.15 * nobs)
itest <- setdiff(inotrain, ivalidate)
train <- df[itrain, ]
validate <- df[ivalidate, ]
test <- df[itest, ]

Alternativamente podríamos emplear la función split(), creando un factor que divida aleatoriamente los datos en tres grupos¹⁶:

set.seed(1)
p <- c(train = 0.7, validate = 0.15, test = 0.15)
f <- sample( rep(factor(seq_along(p), labels = names(p)),
                 times = nrow(df)*p/sum(p)) )
samples <- suppressWarnings(split(df, f))
str(samples, 1)

## List of 3
##  $ train   :'data.frame':    356 obs. of  14 variables:
##  $ validate:'data.frame':    75 obs. of  14 variables:
##  $ test    :'data.frame':    75 obs. of  14 variables:

1.3.5 Evaluación de un método de clasificación

Para estudiar la eficiencia de un método de clasificación supervisada típicamente se obtienen las predicciones para el conjunto de datos de test y se genera una tabla de contingencia, denominada matriz de confusión, comparando las predicciones con los valores reales.

En primer lugar, consideraremos el caso de dos categorías. La matriz de confusión será de la forma:

Observado/Predicción	Positivo	Negativo
Positivo	Verdaderos positivos (TP)	Falsos negativos (FN)
Negativo	Falsos positivos (FP)	Verdaderos negativos (TN)

A partir de esta tabla se pueden obtener distintas medidas de la precisión de las predicciones (serían medidas globales de la calidad de la predicción de nuevas observaciones). Por ejemplo, dos de las más utilizadas son la tasa de verdaderos positivos y la de verdaderos negativos (tasas de acierto en positivos y negativos), también denominadas sensibilidad y especificidad:

• Sensibilidad (sensitivity, recall, hit rate, true positive rate; TPR): \[TPR = \frac{TP}{P} = \frac{TP}{TP+FN}\]

• Especificidad (specificity, true negative rate; TNR): \[TNR = \frac{TN}{TN+FP}\]

La precisión global o tasa de aciertos (accuracy; ACC) sería: \[ACC = \frac{TP + TN}{P + N} = \frac{TP+TN}{TP+TN+FP+FN}\] Sin embargo, hay que tener cuidado con esta medida cuando las clases no están balanceadas. Otras medidas de la precisión global que tratan de evitar este problema son la precisión balanceada (balanced accuracy, BA): \[BA = \frac{TPR + TNR}{2}\] (media aritmética de TPR y TNR) o la puntuación F1 (F1 score; media armónica de TPR y el valor predictivo positivo, PPV, descrito más adelante): \[F_1 = \frac{2TP}{2TP+FP+FN}\] Otra medida global es el coeficiente kappa de Cohen (Cohen, 1960), que compara la tasa de aciertos con la obtenida en una clasificación al azar (empleando la proporción de cada clase): \[\kappa = \frac{2 (TP \cdot TN - FN \cdot FP)}{(TP + FP) (FP + TN) + (TP + FN) (FN + TN)}\] Un valor de 1 indicaría máxima precisión y 0 que la precisión es igual a la que obtendríamos clasificando al azar.

También hay que ser cauteloso al emplear medidas que utilizan como estimación de la probabilidad de positivo (denominada prevalencia) la tasa de positivos en la muestra de test, como el valor (o índice) predictivo positivo (precision, positive predictive value; PPV): \[PPV = \frac{TP}{TP+FP}\] (que no debe ser confundido con la precisión global ACC) y el valor predictivo negativo (NPV): \[NPV = \frac{TN}{TN+FN},\] si la muestra de test no refleja lo que ocurre en la población (por ejemplo si la clase de interés está sobrerrepresentada en la muestra). En estos casos habrá que recalcularlos empleando estimaciones válidas de las probabilidades de la clases (por ejemplo, en estos casos, la función caret::confusionMatrix() permite establecer estimaciones válidas mediante el argumento prevalence).

Como ejemplo emplearemos los datos anteriores de valoraciones de viviendas y estatus de la población, considerando como respuesta una nueva variable fmedv que clasifica las valoraciones en “Bajo” o “Alto” dependiendo de si medv > 25.

# data(Boston, package = "MASS")
datos <- Boston
datos$fmedv <- factor(datos$medv > 25, # levels = c('FALSE', 'TRUE')
                      labels = c("Bajo", "Alto")) 

En este ejemplo, si realizamos un análisis descriptivo de la respuesta, podemos observar que las clases no están balanceadas:

table(datos$fmedv)

## 
## Bajo Alto 
##  382  124

En este caso también emplearemos el estatus de los residentes (lstat) como único predictor. Como se puede observar en la Figura 1.12, hay diferencias en su distribución dependiendo de la categoría, por lo que aparentemente es de utilidad para predecir el nivel de valoración de las viviendas.

caret::featurePlot(datos$lstat, datos$fmedv, plot = "density",
                   labels = c("lstat", "Densidad"), auto.key = TRUE)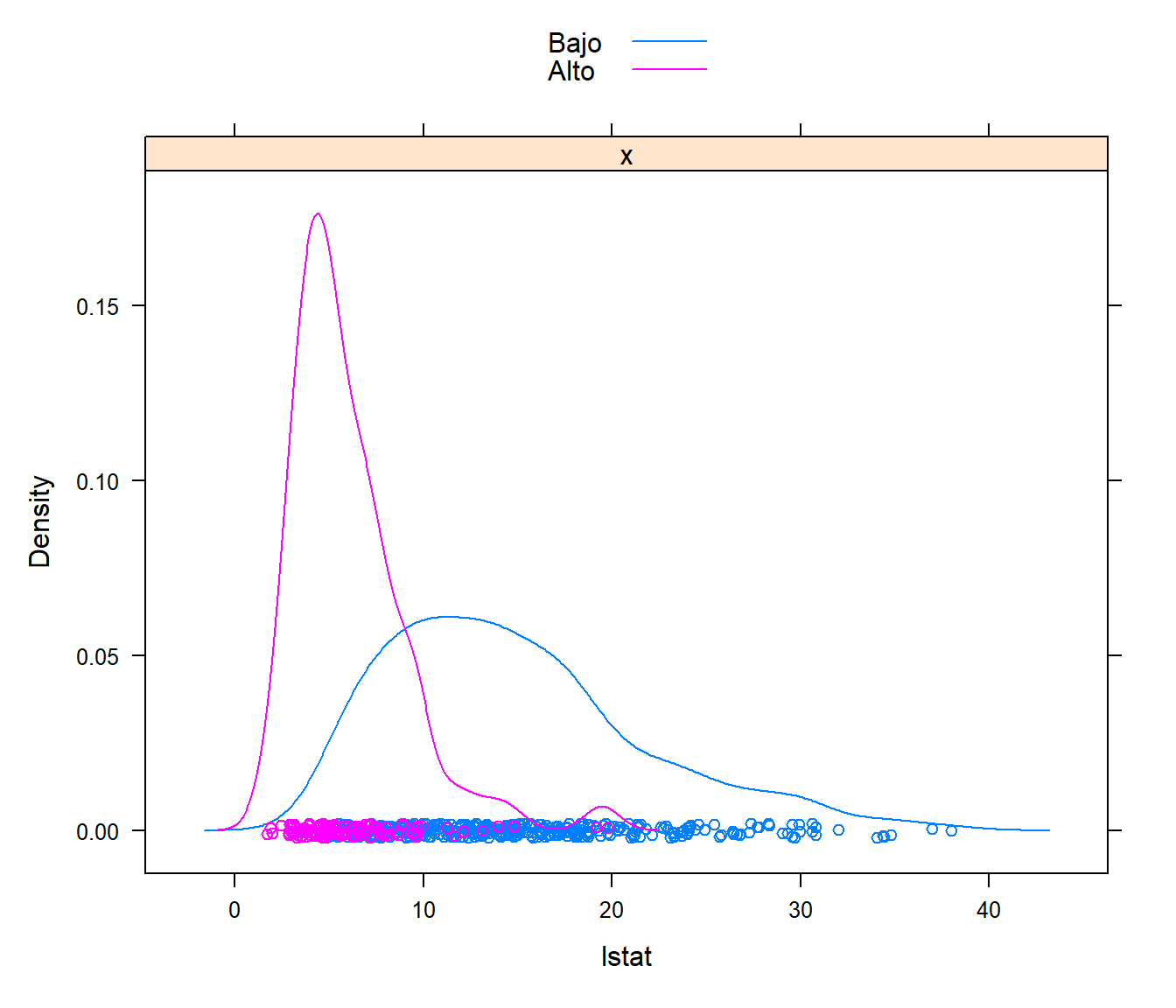

Figura 1.12: Distribución del estatus de la población dependiendo del nivel de valoración de las viviendas.

Como método de clasificación emplearemos regresión logística (este tipo de modelos se tratarán en la Sección 2.2). El siguiente código realiza la partición de los datos y ajusta este modelo, considerando lstat como única variable explicativa, a la muestra de entrenamiento:

# Particionado de los datos
set.seed(1)
nobs <- nrow(datos)
itrain <- sample(nobs, 0.8 * nobs)
train <- datos[itrain, ]
test <- datos[-itrain, ]
# Ajuste modelo
modelo <- glm(fmedv ~ lstat, family = binomial, data = train)
modelo

## 
## Call:  glm(formula = fmedv ~ lstat, family = binomial, data = train)
## 
## Coefficients:
## (Intercept)        lstat  
##       3.744       -0.542  
## 
## Degrees of Freedom: 403 Total (i.e. Null);  402 Residual
## Null Deviance:       461 
## Residual Deviance: 243   AIC: 247

En este tipo de modelos podemos calcular las estimaciones de la probabilidad de la segunda categoría empleando predict() con type = "response", a partir de las cuales podemos establecer las predicciones como la categoría más probable:

obs <- test$fmedv
p.est <- predict(modelo, type = "response", newdata = test)
pred <- factor(p.est > 0.5, labels = c("Bajo", "Alto"))

Finalmente, podemos obtener la matriz de confusión en distintos formatos:

tabla <- table(obs, pred)
# addmargins(tabla, FUN = list(Total = sum))
tabla

##       pred
## obs    Bajo Alto
##   Bajo   71   11
##   Alto    8   12

# Porcentajes respecto al total
print(100*prop.table(tabla), digits = 2) 

##       pred
## obs    Bajo Alto
##   Bajo 69.6 10.8
##   Alto  7.8 11.8

# Porcentajes (de aciertos y fallos) por categorías
print(100*prop.table(tabla, 1), digits = 3) 

##       pred
## obs    Bajo Alto
##   Bajo 86.6 13.4
##   Alto 40.0 60.0

Alternativamente, podemos emplear la función confusionMatrix() del paquete caret, que proporciona distintas medidas de precisión:

caret::confusionMatrix(pred, obs, positive = "Alto", mode = "everything")

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction Bajo Alto
##       Bajo   71    8
##       Alto   11   12
##                                         
##                Accuracy : 0.814         
##                  95% CI : (0.724, 0.884)
##     No Information Rate : 0.804         
##     P-Value [Acc > NIR] : 0.460         
##                                         
##                   Kappa : 0.441         
##                                         
##  Mcnemar's Test P-Value : 0.646         
##                                         
##             Sensitivity : 0.600         
##             Specificity : 0.866         
##          Pos Pred Value : 0.522         
##          Neg Pred Value : 0.899         
##               Precision : 0.522         
##                  Recall : 0.600         
##                      F1 : 0.558         
##              Prevalence : 0.196         
##          Detection Rate : 0.118         
##    Detection Prevalence : 0.225         
##       Balanced Accuracy : 0.733         
##                                         
##        'Positive' Class : Alto          
## 

Si el método de clasificación proporciona estimaciones de las probabilidades de las categorías, disponemos de más información en la clasificación que también podemos emplear en la evaluación del rendimiento. Por ejemplo, se puede realizar un análisis descriptivo de las probabilidades estimadas y las categorías observadas en la muestra de test (ver Figura 1.13):

# Imitamos la función caret::plotClassProbs()
library(lattice) 
histogram(~ p.est | obs, xlab = "Probabilidad estimada", 
          ylab = "Porcentaje (de la categoría)")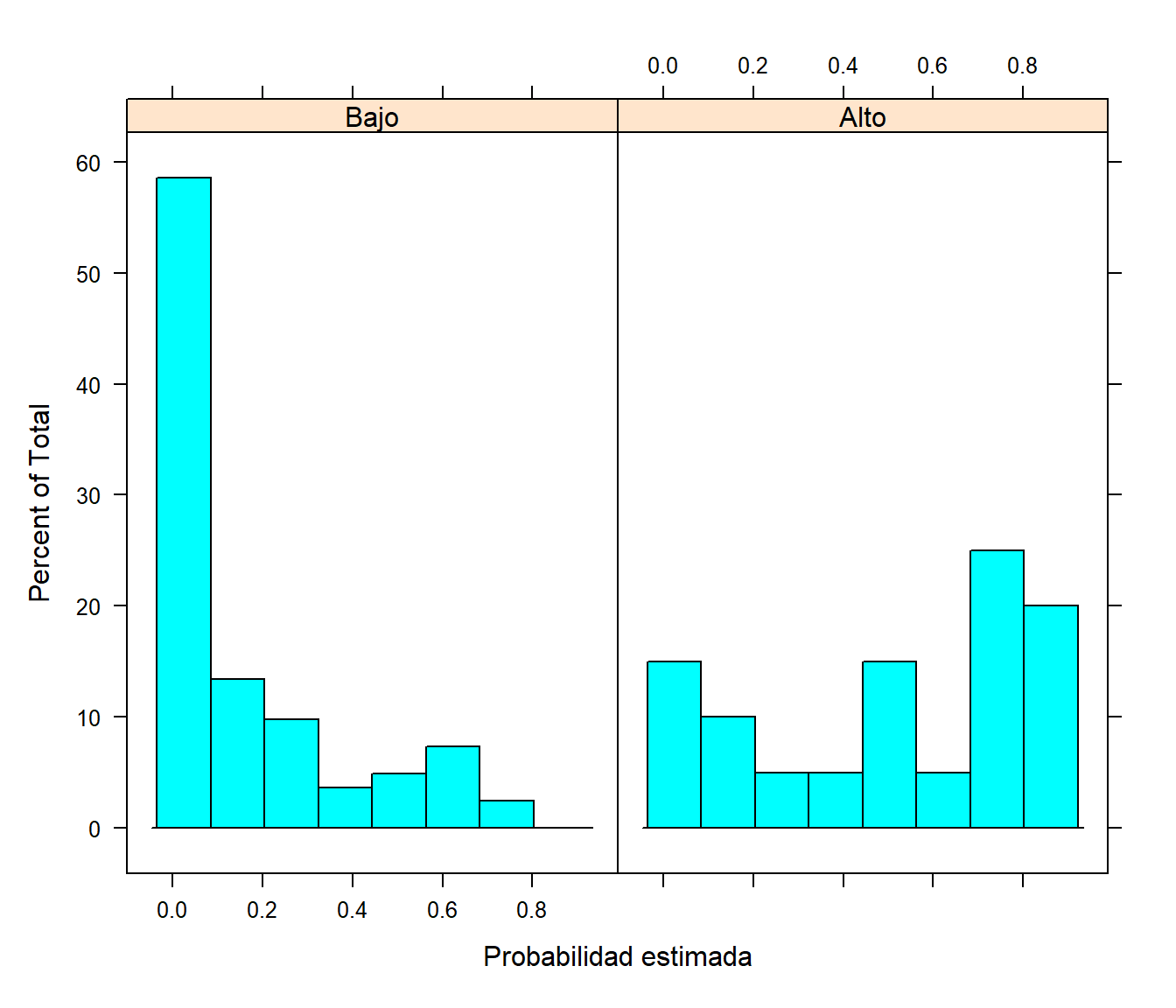

Figura 1.13: Distribución de las probabilidades estimadas de valoración alta de la vivienda dependiendo de la categoría observada.

Para evaluar las estimaciones de las probabilidades se suele emplear la curva ROC (receiver operating characteristics, característica operativa del receptor; diseñada inicialmente en el campo de la detección de señales). Como ya se comentó, normalmente se emplea \(c = 0.5\) como punto de corte para clasificar en la categoría de interés (regla de Bayes), aunque se podrían considerar otros valores (por ejemplo, para mejorar la clasificación en una de las categorías, a costa de empeorar la precisión global). En la curva ROC se representa la sensibilidad (TPR) frente a la tasa de falsos negativos (FNR = 1 \(-\) TNR = 1 \(-\) especificidad) para distintos valores de corte (ver Figura 1.14). Para ello se puede emplear el paquete pROC (Robin et al., 2011):

library(pROC)
roc_glm <- roc(response = obs, predictor = p.est)
plot(roc_glm, xlab = "Especificidad", ylab = "Sensibilidad")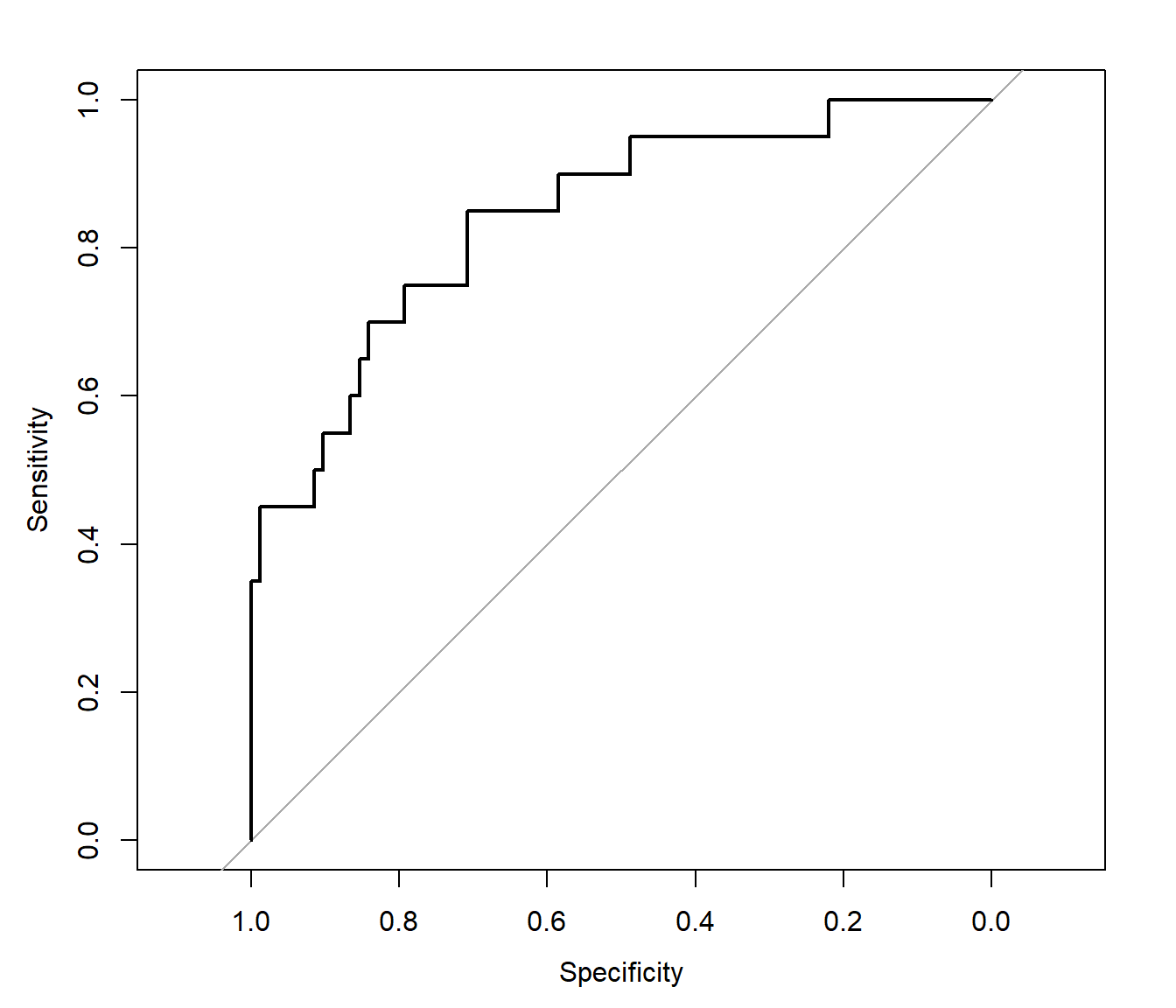

Figura 1.14: Curva ROC correspondiente al modelo de regresión logística.

Lo ideal sería que la curva se aproximase a la esquina superior izquierda (máxima sensibilidad y especificidad). La recta diagonal se correspondería con un clasificador aleatorio. Una medida global del rendimiento del clasificador es el área bajo la curva ROC (AUC; equivalente al estadístico U de Mann-Whitney o al índice de Gini). Un clasificador perfecto tendría un valor de 1, mientras que un clasificador aleatorio tendría un valor de 0.5.

# roc_glm$auc
roc_glm

## 
## Call:
## roc.default(response = obs, predictor = p.est)
## 
## Data: p.est in 82 controls (obs Bajo) < 20 cases (obs Alto).
## Area under the curve: 0.843

ci.auc(roc_glm)

## 95% CI: 0.743-0.943 (DeLong)

Como comentario adicional, aunque se puede modificar el punto de corte para mejorar la clasificación en la categoría de interés (de hecho, algunas herramientas como h2o lo modifican por defecto; en este caso concreto para maximizar \(F_1\) en la muestra de entrenamiento), muchos métodos de clasificación (como los basados en árboles descritos en el Capítulo 2) admiten como opción una matriz de pérdidas que se tendrá en cuenta para medir la eficiencia durante el aprendizaje. Si está disponible, esta sería la aproximación recomendada.

En el caso de más de dos categorías podríamos generar una matriz de confusión de forma análoga, aunque en principio solo podríamos calcular medidas globales de la precisión como la tasa de aciertos o el coeficiente kappa de Cohen. Podríamos obtener también medidas por clase, como la sensibilidad y la especificidad, siguiendo la estrategia “uno contra todos” descrita en la Sección 1.2.1. Esta aproximación es la que sigue la función confusionMatrix() del paquete caret (devuelve las medidas comparando cada categoría con las restantes en el componente $byClass).

Como ejemplo ilustrativo, consideraremos el conocido conjunto de datos iris (Fisher, 1936), en el que el objetivo es clasificar flores de lirio en tres especies (Species) a partir del largo y ancho de sépalos y pétalos, aunque en este caso emplearemos un clasificador aleatorio.

data(iris)
# Partición de los datos
datos <- iris
set.seed(1)
nobs <- nrow(datos)
itrain <- sample(nobs, 0.8 * nobs)
train <- datos[itrain, ]
test <- datos[-itrain, ]
# Entrenamiento 
prevalences <- table(train$Species)/nrow(train)
prevalences

## 
##     setosa versicolor  virginica 
##    0.32500    0.31667    0.35833

# Calculo de las predicciones
levels <- names(prevalences) # levels(train$Species)
f <- factor(levels, levels = levels) 
pred.rand <- sample(f, nrow(test), replace = TRUE, prob = prevalences)
# Evaluación
caret::confusionMatrix(pred.rand, test$Species)

## Confusion Matrix and Statistics
## 
##             Reference
## Prediction   setosa versicolor virginica
##   setosa          3          3         1
##   versicolor      4          2         5
##   virginica       4          7         1
## 
## Overall Statistics
##                                         
##                Accuracy : 0.2           
##                  95% CI : (0.077, 0.386)
##     No Information Rate : 0.4           
##     P-Value [Acc > NIR] : 0.994         
##                                         
##                   Kappa : -0.186        
##                                         
##  Mcnemar's Test P-Value : 0.517         
## 
## Statistics by Class:
## 
##                      Class: setosa Class: versicolor Class: virginica
## Sensitivity                  0.273            0.1667           0.1429
## Specificity                  0.789            0.5000           0.5217
## Pos Pred Value               0.429            0.1818           0.0833
## Neg Pred Value               0.652            0.4737           0.6667
## Prevalence                   0.367            0.4000           0.2333
## Detection Rate               0.100            0.0667           0.0333
## Detection Prevalence         0.233            0.3667           0.4000
## Balanced Accuracy            0.531            0.3333           0.3323

Bibliografía

Breiman, L., Friedman, J., Stone, C. J., y Olshen, R. A. (1984). Classification and Regression Trees. Taylor; Francis.

Canty, A., y Ripley, B. D. (2024). boot: Bootstrap R (S-Plus) Functions.

Cohen, J. (1960). A Coefficient of Agreement for Nominal Scales. Educational and Psychological Measurement, 20(1), 37-46. https://doi.org/10.1177/001316446002000104

Fisher, R. A. (1936). The use of multiple measurements in taxonomic problems. Annals of eugenics, 7(2), 179-188. https://doi.org/10.1111/j.1469-1809.1936.tb02137.x

Fox, J., y Monette, G. (2024). cv: Cross-Validation of Regression Models. https://cran.r-project.org/package=cv

Hyndman, R. J., y Athanasopoulos, G. (2021). Forecasting: principles and practice (3a. ed.). OTexts. https://otexts.com/fpp3. https://otexts.com/fpp3

Kvålseth, T. O. (1985). Cautionary note about R2. The American Statistician, 39(4), 279-285. https://doi.org/10.1080/00031305.1985.10479448

Ripley, B. (2023). MASS: Support Functions and Datasets for Venables and Ripley’s MASS. https://cran.r-project.org/package=MASS

Robin, X., Turck, N., Hainard, A., Tiberti, N., Lisacek, F., Sanchez, J.-C., y Müller, M. (2011). pROC: an open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinformatics, 12, 77. https://cran.r-project.org/web/packages/pROC/

---

10. Se podrían considerar otras funciones de pérdida, por ejemplo con la distancia \(L_1\) sería la mediana condicional, pero las consideraciones serían análogas.↩︎

11. La partición en k-fold CV se suele realizar al azar. Hay que tener en cuenta la aleatoriedad al emplear k-fold CV, algo que no ocurre con LOOCV.↩︎

12. Pueden ser de interés el paquete cv (Fox y Monette, 2024) y también la función cv.glm() del paquete boot (Canty y Ripley, 2024).↩︎

13. Suponiendo que los modelos se pueden ordenar del más simple al más complejo.↩︎

14. Otras implementaciones, como la función caret::plotObsVsPred(), intercambian los ejes, generando un gráfico de dispersión de predicciones sobre observaciones.↩︎

15. Por ejemplo obtendríamos el mismo valor si desplazamos las predicciones sumando una constante (i. e. no tiene en cuenta el sesgo). Lo que interesaría sería medir la proximidad de los puntos a la recta \(y=x\).↩︎

16. Versión “simplificada” (y más eficiente) de una de las propuestas en el post https://stackoverflow.com/questions/36068963. En el caso de que la longitud del factor f no coincida con el número de filas (por redondeo), se generaría un warning (suprimido) y se reciclaría.↩︎